多编组铰接车辆的平顺性时域分析与优化
2022-02-17陈俊李艳杨蔡进张德华张卫华
陈俊, 李艳, 杨蔡进*, 张德华, 张卫华
(1.西南交通大学 牵引动力国家重点实验室, 四川 成都 610031;2.成都西南交通大学设计研究院有限公司, 四川 成都 610031)
0 引言
随着城市化进程的发展,城市人口规模不断扩大,居民的出行需求也显著增多。由公交车、地铁和轻轨等组成的城市公共交通运输体系的运输能力逐渐趋于饱和。多编组铰接车辆通过多车体模块铰接实现中等运量,可形成对现有城市公共交通运输体系的有益补充,缓解当前日趋严重的交通运输压力。
多编组铰接车辆在行驶中受路面不平顺激励作用而发生振动。由于车身长大,车体振动经过传播和叠加,形成复杂振动效应,影响车辆行驶平顺性和操纵稳定性,因此对于城市客运车辆,具有良好的平顺性非常重要。通常,悬架参数优化是改善车辆平顺性的重要手段,如Niu等[1]提出了一种计算效率较高的平面双横臂悬架全范围动力学模型,实现悬架几何形状的快速优化设计。Driehmer等[2]基于粒子群算法与二次规划算法,建立了悬架最优参数选取原则。Issa等[3]采用HHO算法优化被动悬架参数。车辆基于上述的被动悬架参数优化方法难以匹配不同路面条件,不能达到最佳的平顺性状态。围绕悬架控制技术,国内外学者开展了有效研究,并取得一定成果。为改善悬架振动性能,Sun[4]提出了一种延时加速度反馈控制方法。对于四角互联空气悬架难以发挥多可控结构优势的问题,孙丽琴等[5]设计了MPC控制器,实现了互联空气悬架之间的协同控制,改善了整车性能。Nichitelea等[6]提出了一种自适应谐波控制算法,并与多种控制方案进行对比,该方法具有更好的性能。Ghazally等[7]提出了一种用于主动悬架系统振动控制的最优滑模控制器,并采用粒子群算法求得最优控制器的参数,具有结构简单易调节的特点。Satyanarayana等[8]通过比对基于LQR控制的主动悬架使用情况,确定了两自由度1/4汽车模型的被动悬架参数。Rath等[9]考虑了1/4车辆主动悬架模型,设计了一种高阶终端滑模控制器。秦东晨等[10]采用系统建模和机器视觉的方法研究了一种基于完全预瞄的主动悬架控制系统。
除上述研究外,基于悬架控制技术也可以改善诸如多轴特种车辆和半挂车等特殊铰接车辆的平顺性性能。孙帮成[11]建立了3节浮车式虚拟轨道列车1/2模型,分析线性悬架参数对列车平顺性影响。朱亚夫等[12]建立三轴车辆的1/2系统模型,并设计一种基于滑模控制器的主动悬架系统。在上述研究中,尽管采用了多种方法对不同车辆进行了平顺性的分析与优化,但研究对象很少涉及多节编组车辆,且研究的方向没有从车辆的编组连接关系着手,很少体现不同编组之间振动特性的差异,在主动悬架控制的研究中,针对多编组车辆提出的主动控制悬架较少。
多编组铰接车辆,特别是长编组铰接车辆可用于公共运输,提升城市客运能力,是城市轨道交通未来发展的一个重要方向。目前,针对这类新制式运输系统的研究还不够充分,本文针对上述系统的平顺性问题开展前期研究,主要工作包括:建立具有n节编组铰接车辆的振动模型,通过仿真分析了4节编组车辆系统的平顺性特点,研究基于悬架系统的参数优化和主动控制改善平顺性的方法。相关研究可为系统研制与应用提供理论依据,具有一定理论和工程意义。
1 多编组铰接车辆振动模型
图1所示为简化的n节编组铰接车辆系统。考虑车体垂向、侧倾、俯仰和车轮垂向运动[13],并考虑悬架非线性阻尼特性,本节建立车辆系统的多自由度振动模型,过程如下。

图1 多编组铰接车辆示意图Fig.1 Diagram of the multi-articulated vehicle
1.1 基本描述
假设zi表示第i节车体的垂向位移,φi表示该车体的侧倾角,θi表示该车体的俯仰角,wi,j表示该车体上j位置车轮的垂向位移,这里指标i=1, 2,…,n表示编组序号,j=fl、fr、rl和rr分别表示左前、右前、左后和右后处车轮或悬架位置,且为了统一性,下文将采用相同记号规定。系统具有7n个自由度,且描述系统振动的广义坐标列阵q可定义为
(1)
其中
qi=[zi,φi,θi,wi,fl,wi,fr,,wi,rl,wi,rr]T。
(2)
1.2 悬架系统
本文中悬架系统的力学特性可表征为线性刚度Ks和具有分段线性函数[14]的非线性阻尼Cs,如图2所示,其中:阻尼系数Cs可根据附录A1中参数计算获得。悬架弹簧作用力与等效弹簧变形量成正比。下文仅以第i节车体左前轮处悬架作用力为例,说明计算过程。其他悬架作用力分析过程类似,不再赘述。
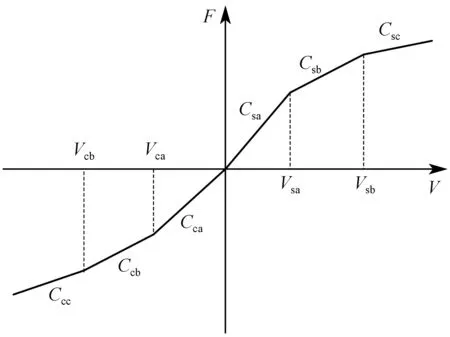
图2 悬架阻尼特性Fig.2 Suspension damping characteristics
假设车体发生小角度转动,则左前轮处悬架两端垂向相对位移si,fl可表示为
si,fl=zi+bφi+lθi-wi,fl。
(3)
式中:b为半倍轮距;l为半倍轴距。将式(3)对时间t求导一次,可得到悬架两端点的相对速度为
(4)
利用式(3)和式(4),该悬架作用力Fi,fl表示为
(5)
当系统使用主动悬架时,其作用力只需在方程(5)等号右端中增加控制力项即可。
1.3 车间铰接系统
车间铰接系统实现车体间的机械连接。本节采用约束模型来描述车间铰接处力学行为,在不考虑转向的情况下,将铰接式公共交通车辆常采用的盘式铰接器等效为转动副。根据转动副约束特点,相邻车体的铰接位置的垂向位移相等,在不考虑车体变形的情况下,相邻车体的侧倾角相等,以第i(i= 1, 2,…,n-1)个车间铰接为对象的约束方程为
(6)

(7)
其中,d为半倍车间轴距,因此,铰接系统的等效约束方程表示为
。
(8)
1.4 路面激励和轮胎力
路面通常具有随机不平度,形成车体振动的激励源。假设qi,fl表示第i节车体左前轮胎处路面激励,且基于滤波白噪声方法可定义为[15-16]
(9)
式中:n1表示下截止空间频率,取0.01 m-1;v表示车速;Gq(n0)表示与路面等级相关的不平度系数。本文考虑B级路面条件,故该系数为64/10-6m3;wni,fl表示白噪声输入。为匹配不同车速工况,本文白噪声的采样时间间隔设置为0.1v[16]。另一方面,车轮在同一区域受到路面激励具有一定的相干性。因此,参考文献[17],设第i节车体右前轮处路面激励白噪声输入为
(10)
代入式(9),得右前轮处路面激励qi,fr。此外,当车辆匀速直线行驶时,车辆后轮与前轮处路面激励存在时间滞后性,故后轴左右轮的路面激励可表示为
qi,rl(t)=qi,fl(t-τ),qi,rr(t)=qi,fr(t-τ),
(11)
式中τ表示延迟时间,且有τ=2l/v。最后根据前后路面输入相关性的状态空间方程得到后轮处路面激励输入[18-19]。设轮胎垂向刚度为Kgw,则轮胎力可表示为
Fi,j=-Kgw(wi,j-qi,j),
(12)

图3 路面不平顺功率谱密度图Fig.3 Power spectral density map of road roughness

图4 路面不平顺激励时域图:(a)左轮;(b)后轮;(c)右轮Fig.4 Time domain diagram of road surface irregularity excitation: (a)left wheel; (b)rear wheel; (c)right wheel
图3表示车速60 km/h时左、后与右轮路面输入的功率谱密度图。图4分别为左轮路面、后轮路面和右轮路面的垂向激励时域图,取第i+1节车的四轮激励为第i节车对应的四轮滞后激励,滞后时间为(2l+2d)/v,以此得到铰接车辆多轮路面输入模型。
1.5 车辆系统振动方程
基于上文的推导,车辆系统的振动方程可表示为
(13)
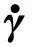
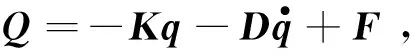
(14)
式中:K为刚度矩阵;D为阻尼矩阵;F主要为重量和路面激励力向量,其中刚度矩阵具体形式为
K=diag[K1,…,Ki,…,Kn]7n×7n,
(15)
式中Ki表示第i(i= 1,2,…,n)节编组的刚度矩阵,其具体形式为
(16)
阻尼矩阵D的形式与刚度矩阵相似;但由于采用非线性阻尼,因此各悬架处的实际阻尼值可能各不相同。F主要包含路面激励作用产生的垂向作用力和车体所受重力,计算公式为
(17)
式中Fi表示第i(i=1,2,…,n)节编组的作用力,由下式计算:
(18)
M表示车辆系统的质量矩阵,且有
M=diag[M1,M2,…,Mi,…,Mn]7n×7n,
(19)
式中Mi= diag[mc,Ixx,Iyy,mw,mw,mw,mw],其中mc表示车体质量,mw表示簧下质量,Ixx和Iyy分别为俯仰和侧倾方向的转动惯量。
2 多编组铰接车辆平顺性时域评价指标与分析
采用四阶龙格库塔法求解车辆振动方程(13),获得系统振动响应,并结合相关评价指标,分析系统的平顺性特点。
2.1 平顺性评价指标
本文选取车体的垂向、侧倾角和俯仰角加速度均方根作为车辆平顺性的评价指标[19],其相关计算公式为
(20)
车轮相对动载荷均方根能较好反映出轮胎与地面的附着特性,当相对动载荷均方根过大时车轮附着力减小,车轮可能会脱离地面,故本文采用该指标来评价车轮与路面接触性能[21],其计算公式为
(21)
式中:g为重力加速度;σi,j为车轮无量纲的相对动载荷均方根。
2.2 多编组铰接车辆平顺性特点分析
不失一般性,本节以n=4节编组铰接车辆为例,结合附录中表A1的车辆参数,仿真分析系统在车速30、45、60、75、90 km/h工况下的振动响应,并基于上文相关指标计算得到车体的垂向加速度、俯仰角加速度、侧倾角加速度和车轮相对动载荷均方根,研究车辆系统的平顺性,主要结果见图5—8。
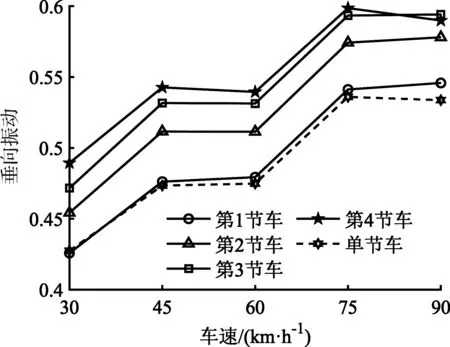
图5 垂向振动加速度均方值Fig.5 RMS value of vertical vibration acceleration

图6 侧倾角加速度均方根Fig.6 RMS value of roll angle acceleration
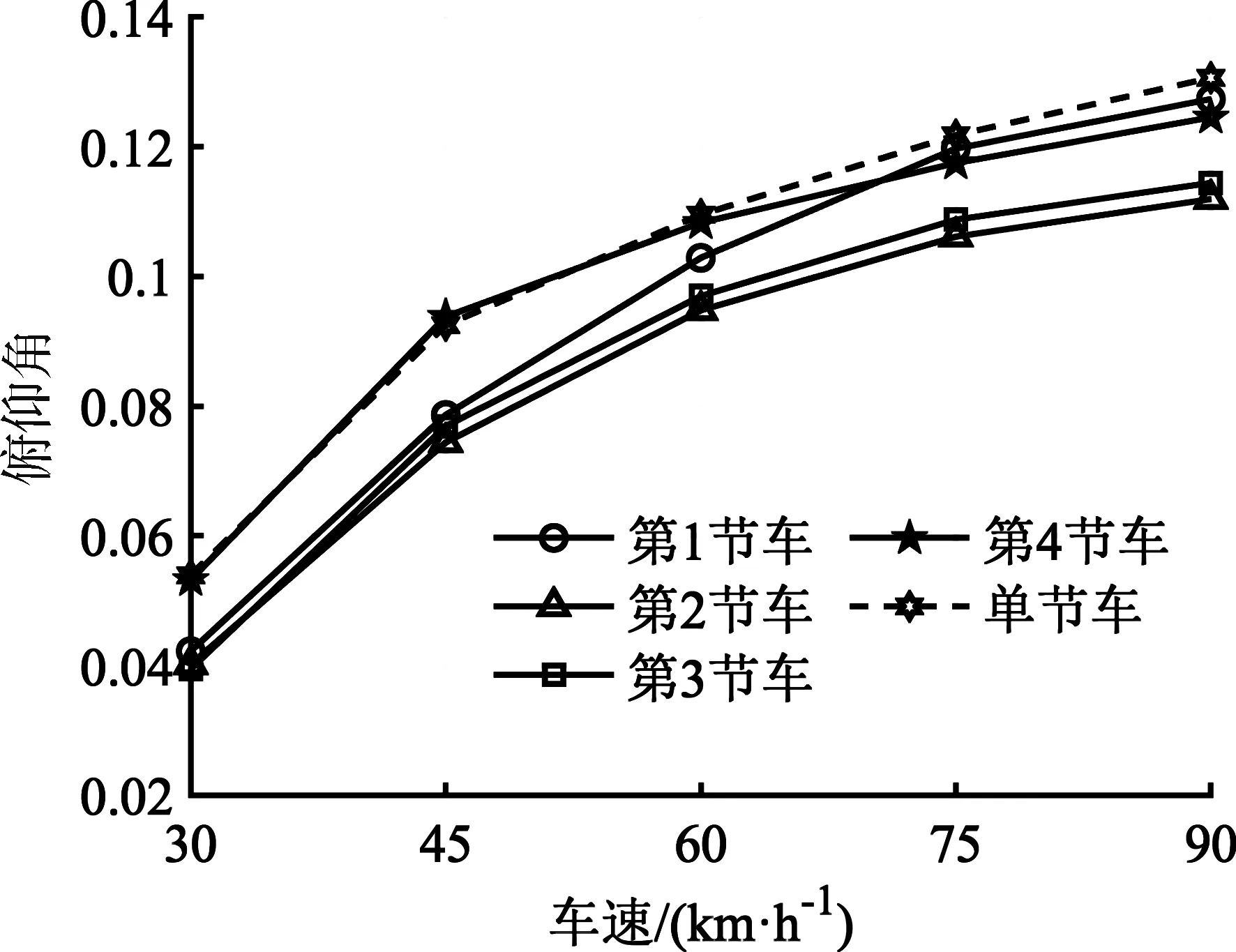
图7 俯仰角加速度均方根Fig.7 RMS value of pitch angle acceleration
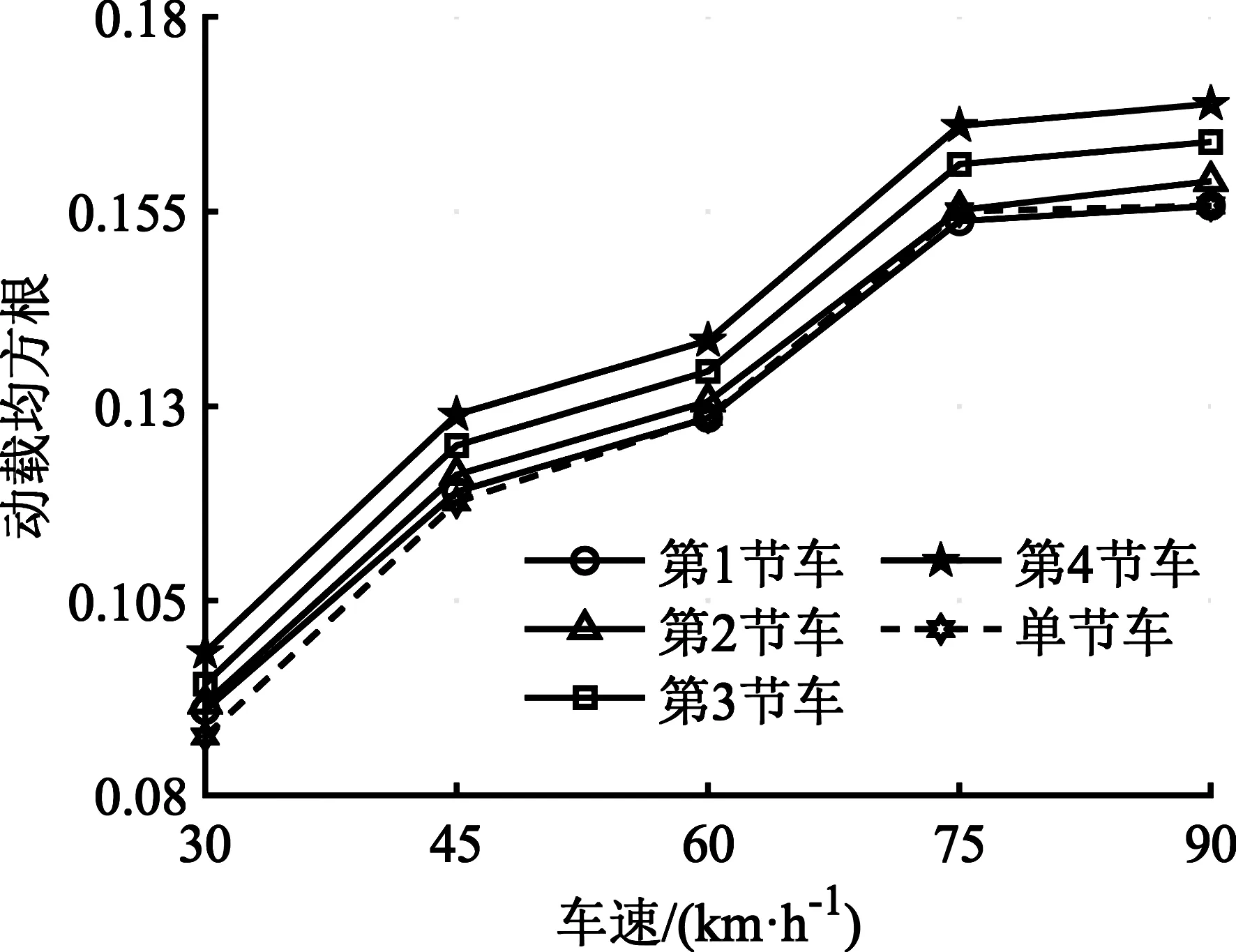
图8 车轮相对动载荷均方根Fig.8 RMS value of wheel relative dynamic load
由图5可见,在一定车速下各节车体的垂向振动加速度均方根值呈现出依次增大的趋势,这是由车体振动传播、叠加以及刚体运动造成,此外,车速增加会导致垂向激励作用增加,从而使各节车体的垂向振动加速度均方根值变大,但首车垂向振动加速度均方根与单车系统的垂向振动加速度均方根相接近,且两者接近程度随车速增加并无显著变化。
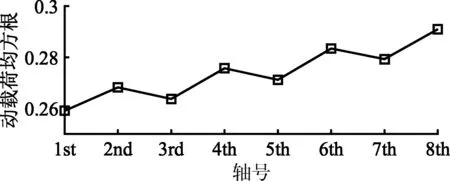
图9 时速60 km/h不同车轴车轮相对动载荷均方根Fig.9 RMS value of wheel relative dynamic load of the different axles at 60 km/h
图6、7分别为车辆的侧倾角和俯仰角的加速度均方根值随车速增加的变化图。图6表明各节车体的侧倾角加速度均方根值随车速增加先增大后减小,单车系统的侧倾角加速度均方根值相比与各编组在各个速度下都更大,由于受车间铰接作用,因此各节车体侧倾振动具有一致性。如图7所示,各节车体的俯仰角加速度均方根值随速度增加而增大,从车间分布来看,该评价指标在首车到第二节编组之间减小,随后依次增加,且单车系统的俯仰角加速度均方根分布情况与尾车类似。
由图8可见,各编组车轮的相对动载荷均方根平均值随车速增加而增大,而单车系统车轮的相对动载荷均方根值比各编组都要小。图9表明从车轴方向比较,铰接车辆车轮的相对动载荷均方根平均值近似地按线性方式增长。
3 车辆平顺性优化
由上文仿真结果可知,随着车速增加,车辆的垂向振动与俯仰振动加剧,且相比于侧倾运动,车辆的垂向与俯仰振动对平顺性具有更重要的影响[22],为抑制车辆振动,提升车辆整体的平顺性,本文分别通过悬架参数优化与主动悬架控制来提升车辆的平顺性。
3.1 基于粒子群算法的悬架参数优化
本节基于自适应惯性权重粒子群算法[23],针对悬架减震器阻尼特性参数进行优化设计,考虑到悬架动扰度对悬架刚度约束,仅对悬架阻尼系数进行优化,包括减震器压缩低速段系数Cca、压缩中速段系数Ccb、减震器拉伸低速段系数Csa和拉伸中速段系数Csb,以及相应低速过渡节点速度Vca和Vsa,并以最小化各节车体的垂向、俯仰角和侧倾角加速度均方根为优化目标,此外,本节在优化过程中还考虑下列约束条件:① 为保证阻尼大小,悬架阻尼比ζi,j满足:
ζl≤ζi,j≤ζu,
(22)
式中ζl和ζu分别取0.2和0.4[24];②为避免悬架行程过大而触及限位块,悬架动挠度均方根应小于限位行程的1/3[25],即
RMS(si,j)≤[fd]/3,
(23)
式中[fd]为9 cm;③轮胎应具有足够的附着力,满足车轮脱离地面的概率小于0.15%,保证操纵稳定性,其相对动载荷均方根应小于1/3[25],即
RMS(σi,j)≤1/3。
(24)
基于优化目标和约束条件,取粒子群规模为200,经过50次迭代后,得到优化后的减震器阻尼特性参数为:Cca=9 844.27 N·s/m,Ccb=7 764.07 N·s/m,Csa=13 809.15 N·s/m,Csb=9 620.40 N·s/m,Vca=-0.21 m/s和Vsa=0.23 m/s。表1给出了在悬架参数优化前后,以车速60 km/h工况下所有编组平顺性指标的平均值大小。
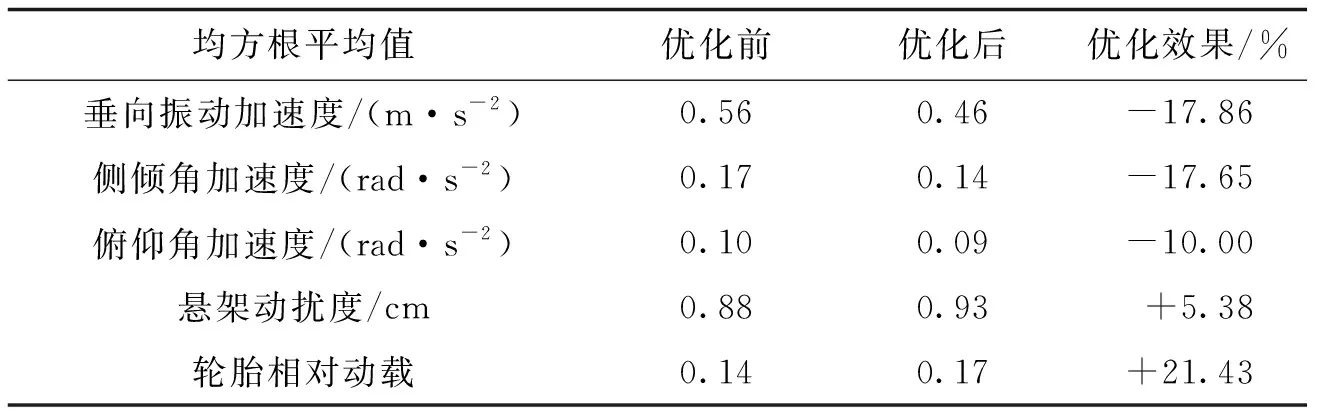
表1 时速60 km/h铰接车辆平顺性优化效果Tab.1 Optimization of the ride comfort of articulated vehicles at 60 km/h
由表1可见,悬架参数优化后车体的垂向、侧倾和俯仰加速度均方根均明显减小,虽然悬架的动挠度和轮胎相对动载指标有所增加,但仍处于设定范围内,综上表明车辆平顺性得到了有效改善。
3.2 主动悬架控制
悬架性能直接影响着车辆平顺性,而被动悬架通常只能在特定的情况下达到最优减振效果,难以适应不同的道路和使用状况。本节选取车体垂向、侧倾角和俯仰角加速度均方根,以及悬架与轮胎的动挠度均方根作为性能优化目标,采用优化后的悬架参数,通过悬架主动力的控制,实现多编组铰接车辆在复杂运行环境下具有良好的乘坐舒适性和平顺性。令控制系统的状态变量为
(25)
式中
(26)
控制系统的输出向量为
(27)
式中
(28)
控制力输入向量为
U=[u1,j,u2,j,…,ui,j]T=U1+U2,
(29)
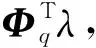
(30)


图10 主动悬架控制示意图Fig.10 Active suspension control flow diagram
考虑车辆振动方程(13),系统控制方程可表示为
(31)
式中:A为系统的状态矩阵;B为系统的输入矩阵;向量W包含多轮路面激励白噪声输入、车间约束力与补偿控制力U1;C和E分别为系统的输出矩阵与传递矩阵。
3.2.1LQG控制器设计
本节基于LQG控制方法,通过优化设定的目标性能指标来改善车辆平顺性,其中拟优化性能指标函数J为
(32)
其中:A1、A2、A3、A4和A5为各性能指标的加权系数;r1为控制力的加权系数。将式(31)代入式(32)得到
(33)

(34)
其中,S为反馈增益矩阵,且有
(35)
式中P可由Ricatti方程求得[26]
PA+ATP-PBR-1BTP+Q=O。
(36)
3.2.2 基于主动悬架控制仿真结果
考虑加权系数A1= 1.00,A2= 2.98,A3= 0.85,A4= 203.60,A5= 2 290和r1= 10-8。本节基于悬架主动力控制,分析车速为60 km/h时车辆平顺性,其中车辆平顺性的优化前后结果比较见图11和表2所示。表2给出了经主动控制前后,评价指标在所有编组车体的均方根平均值,图11(a),图11(b)和图11(c)分别表示控制前后首节编组车辆垂向、侧倾和俯仰方向的加速度大小。由图11与表2可以看出,车辆的振动加速度得到不同程度的改善,且使对平顺性影响更大的垂向与俯仰方向的振动加速度均方根优化效果更好,尽管轮胎动载荷均方根有所增加,但其值小于1/3,处于约束范围内。

表2 时速60 km/h车辆平顺性控制优化效果Tab.2 Optimisation of ride comfort control for articulated vehicles at 60km/h
4 结论
本文考虑悬架非线性阻尼特性,建立了n节编组铰接车辆系统的振动方程,结合评价指标对系统平顺性问题进行仿真分析,研究发现了多铰接车辆存在由首车至尾车车体垂向振动加速度均方根值依次变大等振动特点。同时,基于该车辆振动特点,为进一步提高车辆平顺性,本文通过粒子群算法优化悬架参数并采用主动悬架控制,其中,主动悬架控制器设计采用车间约束力补偿和LQG控制方法。仿真结果显示,相比于未优化悬架参数的被动悬架,实施优化和控制后的主动悬架,车体在垂向、侧倾和俯仰方向的振动表现出明显的改善,其对应的平顺性评价指标(垂向、侧倾和俯仰方向加速度均方根值)分别减少了48.29%,24.79%和54.44%。上述结果表明本文提出的主动悬架控制能有效改善该多编组铰接式车辆的平顺性。
附录

表A1 车辆主要参数Tab.A1 Main parameter values of the vehicle
