自适应反归一化改进多层神经网络轴流转桨水轮机协联功率预测

陆文玲, 夏家辉, 孔繁镍*

(1.南宁职业技术学院 智能制造学院, 广西 南宁 530008;2.广西大学 电气工程学院, 广西 南宁 530004)

0 引言

为了保证水电机组运行效率,机组运行部门一般要对新安装或长时间运行的轴流转桨水轮机进行协联、非协联试验,获取机组最优运行调控规律及效率等数据,为制定水电机组持续高效运行操作规范提供依据,但协联、非协联试验需要大量的经济和时间成本[1],通常只能获取有限的数据量。通过搭建预测模型可以有效弥补试验数据不足,指导现场测试,提高测试效率。

轴流转桨水轮机系统天然具有复杂的水机电耦合特性,因而其物理预测模型呈现高度非线性化[2]。考虑到实际协联试验现场存在诸如蜗壳、管壁压力、摩擦系数等随时波动问题,无法保证物理模型的准确性和普适性。数学模型通过数据学习抽象各输入输出特征关系,使其具备相对广泛的适用性,本文通过搭建神经网络数学模型进行水轮机协联数据预测。

神经网络是具有强大的非线性数据拟合能力,诸多学者开展相关的应用基础研究。文献[3]结合BP(back propagation)神经网络建立水轮机组非线性模型,实现流量和力矩的仿真。BP神经网络可实现复杂非线性映射,但存在收敛速度慢,梯度下降法容易陷入局部最优[4]等问题。针对收敛问题,文献[5]提出了一种多层人工神经网络过电压预测模型,通过增加隐藏层数目提高模型收敛速度。当激活函数为sigmoid进行权阈值修正时,需要从输入层至输出层逐层链式求导,当层数过深时,多层导数连续相乘会产生梯度消失,参数无法更新。考虑到梯度下降算法存在局限性,文献[6]采用Adam优化器进行改进,但只介绍Adam算法[7]流程,未详细推导其与神经网络参数更新结合过程,而且其优化器的学习率等重要参数设置为定值,其收敛速率和迭代精度无法达到最优。数据处理方面,文献[8-10]将历史数据分为训练集和测试集,对其归一化处理,实现对历史数据预测，但都未体现反归一化过程对于实际预测的作用,仅将归一化公式按原格式逆运算,没有具体详细说明对应参数的物理意义。

针对上述不足,本文提出一种改进多层神经网络(improved multilayer neural network,IMNN)预测模型,基于BP网络框架基础上,为提高网络收敛速度和避免梯度消失问题,将隐藏层数目扩展为有限数目,从数学角度分析利用激活函数Rule加快网络计算速度和收敛的原理。由于梯度下降法存在局部最优、收敛缓慢等问题,因此采用粒子群算法优化Adam优化器参数设置。采用L2正则化防止过拟合现象。本文对IMNN模型自身运作原理及优化方面进行详细的数学推导,并针对神经网络实践预测应用提出自适应反归一化区间策略,结合水轮机协联与非协联试验证明该数学模型和自适应策略的有效性。

1 改进多层神经网络设计

1.1 BP神经网络

BP神经网络[11]结构如图1所示。BP神经网络主要包含2个运算过程:前向传播和反向学习。数据样本由输入层进入网络,经权值和阈值计算后抵达隐藏层,在隐藏层经激活函数作用后,通过新一轮的权、阈值计算到达输出层,输出层输出预测值。反向学习是依据损失函数对网络中的权值和阈值进行修正,使网络误差在精度范围内。

BP神经网络主要涉及到输出层输出y计算、权值Wij计算及更新[12]。

图1中xj为输入层第j个神经元接受样本,bi分别为隐藏层第i个神经元阈值,Vi为层间权值。

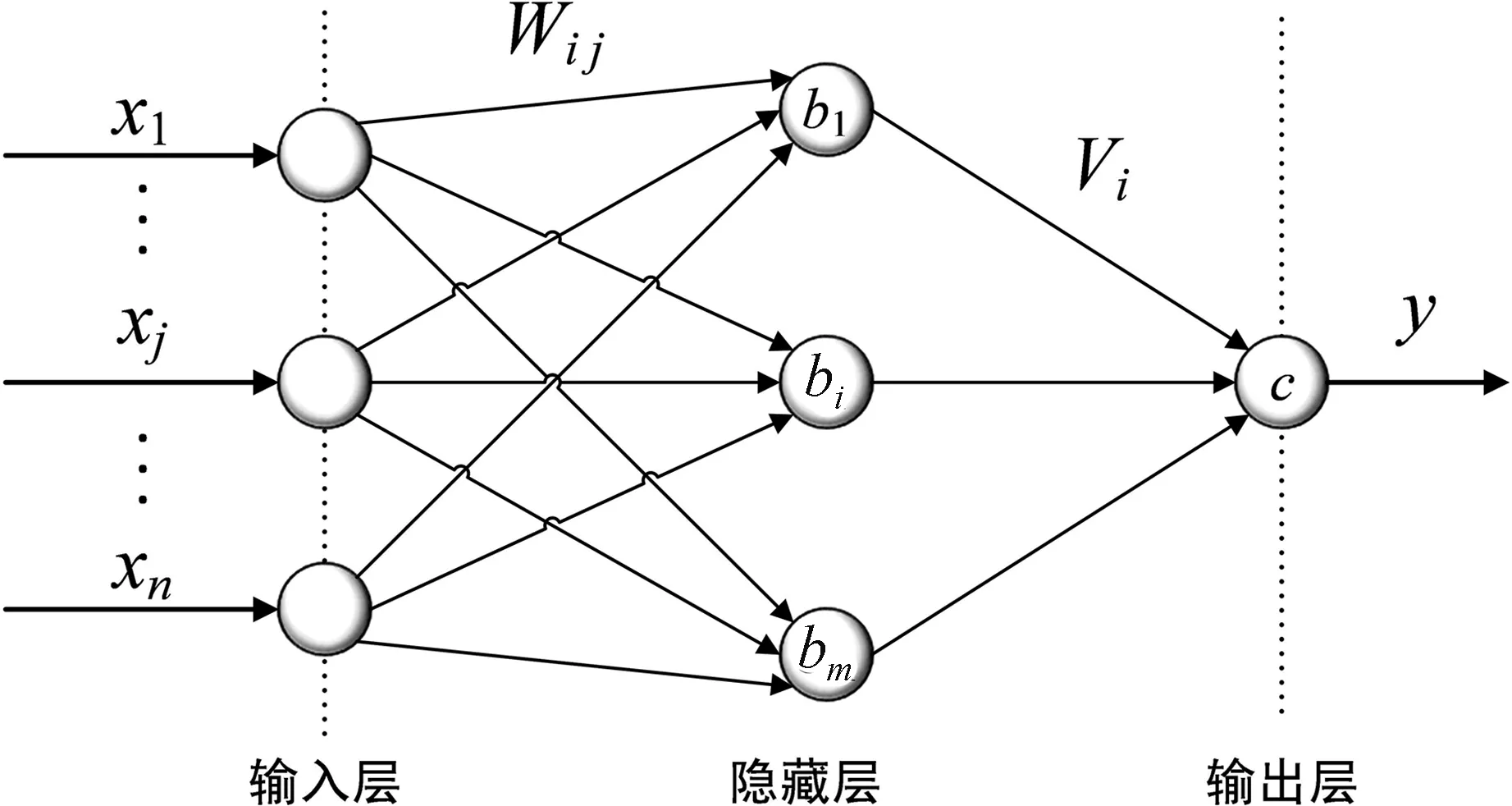
图 1 BP神经网络结构Fig.1 Structure of BP neural network

1.2 IMNN网络框架

为提高网络收敛速度,同时防止层数过深导致的梯度消失问题,改进多层神经网络在BP结构基础上将隐藏层数目扩展为3。其结构如图2所示:

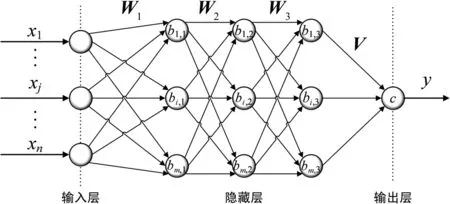
图2 IMNN结构Fig.2 Structure of IMNN

选Rule函数为激活函数:

R(x)=max(0,x)。

(1)

如图2所示IMNN的前向计算过程的矩阵表达式为

(2)

式中:W1、W2、W3为权值矩阵；bk=[bk1,bk2,bk3]T,(k=1,2,3)为阈值向量；V=[V1,V2,V3]为隐藏层最后层与输出层间的权值向量；y为输出值向量。

推导得到Rule函数梯度更新公式:

(3)

样本p权阈值的梯度为

(4)

1.3 过拟合正则化与梯度优化器

过拟合现象是模型对当前数据拟合过深,对未学习的新数据难以做出正确的判断,模型缺乏泛化力。采用L2正则,防止数值模型过拟合,在损失函数中加入正则项来表征模型的复杂度,

。

(5)

总样本的损失函数定义为

。

(6)

式(5)-(6)中:λ为正则项系数；ξ=[W1,W2,W3,V]T为总权值矩阵。梯度公式(4)进一步更新为

(7)

(8)

(9)

，

(9)

，

(10)

，

(11)

。

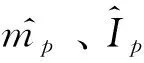
(12)

同理可以推导得到bi、Vi的更新公式,

，

(13)

。

(14)

1.4 PSO优化梯度参数

为了提高Adam优化器参数收敛速度和准确度,本文利用粒子群优化算法[13-14]对网络参数进行优化。粒子群的适应值函数[15-16]选取为IMNN迭代后的总损失函数,3个待优化粒子为Adam改进梯度法学习率c1,一阶、二阶动量系数β1、β2。Adam参数优化流程如图3所示。

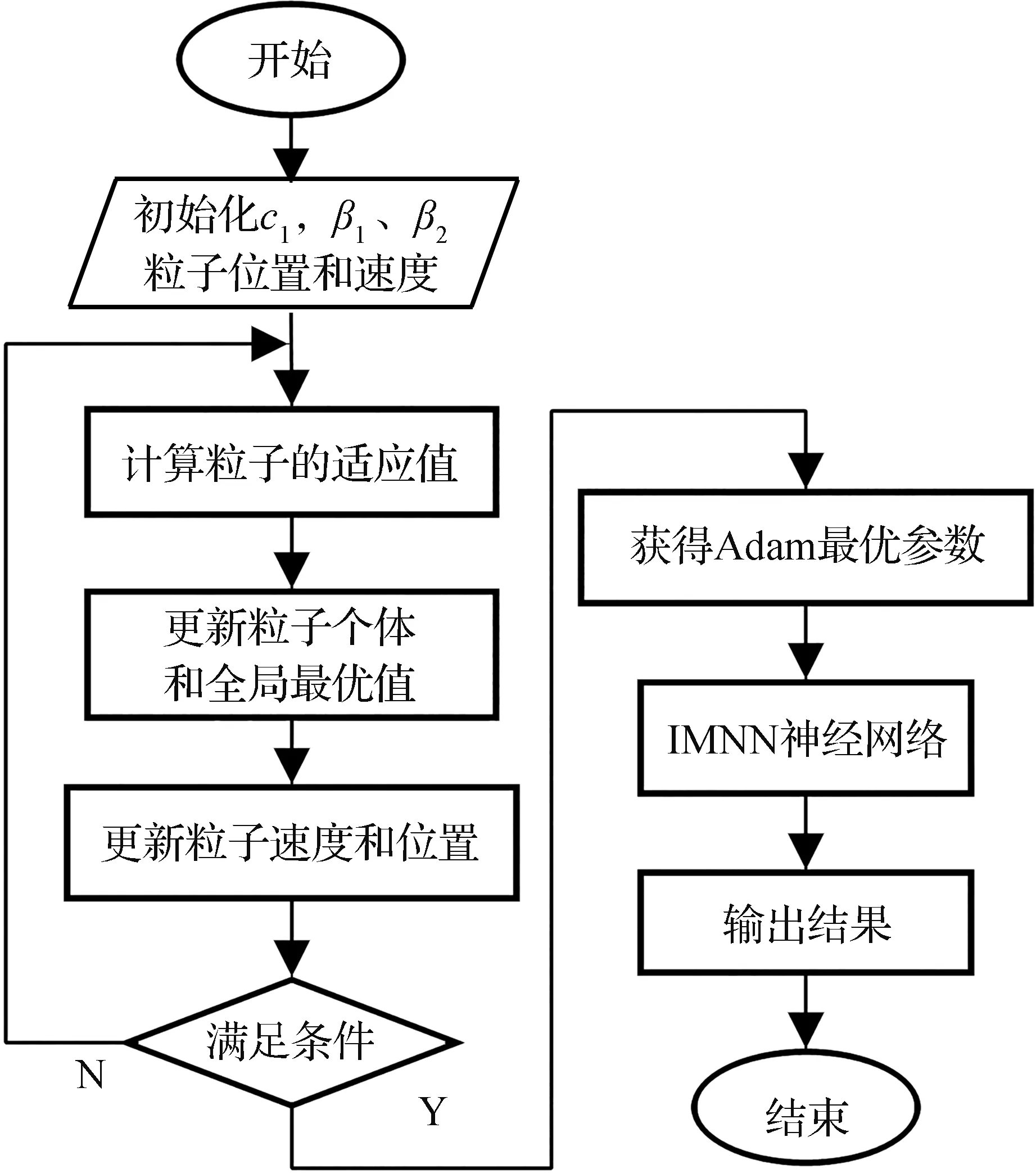
图3 粒子群算法优化Adam参数流程图Fig.3 Flow chart of the optimized Adam parameters based on PSO

2 自适应反归一化区间策略

为了统一各特征xj的量纲,通常需要对样本数据x=[x1,x2,…xj,…,xn]T采用归一化处理,采用归一化公式[11]为

(15)

式中:α=0.95;β=0.05;xmax、xmin分为为输入特征向量中的最大值和最小值。

(16)

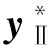
对应学习样本xⅠ和预测样本xⅡ,其反归一化公式为

,

(17)

,

(18)

式(17)中:YⅠ,max=tmax;YⅠ,min=tmin。对于实际预测场景,式(18)中值YⅡ,max和YⅡ,min一般是未确定,故需要合理分析、逼近,最终找到一组合适的数据替代YⅡ,max和YⅡ,min的值,从而实现式(18)反归一化运算。

为了找到一组数Nmax和Nmin实现YⅡ,max=Nmax,YⅡ,min=Nmin。Nmax和Nmin的数值替代效果越逼近,式(18)计算的模型预测输出越接近真实情况。为判断Nmax和Nmin取值,本文构建设计了如下方案:

方案1:直接选取Nmax和Nmin为学习样本期望值的最大值最小值,即Nmax=tmax,Nmin=tmin。

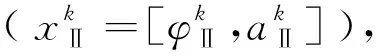
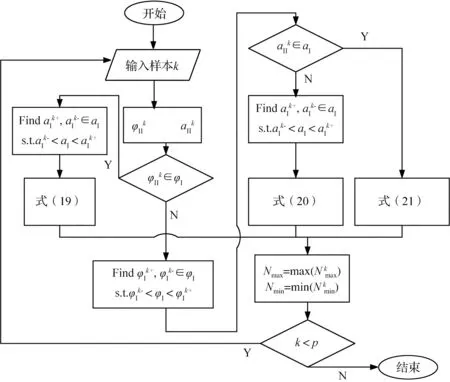
图4 自适应区间策略方案2流程图Fig.4 Flow chart of adaptive interval Strategy 2

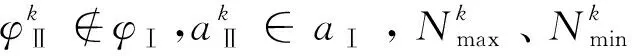
(19)

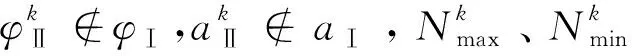
(20)

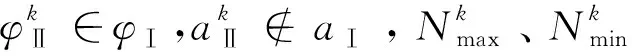
(21)

方案3:假定获得了现场试验的真实值,即真实值向量YⅡ已知,故能获取YⅡ，max和YⅡ，min的值,则Nmax=YⅡ，max,Nmin=YⅡ，min。

3 算例分析

3.1 梯度优化

在保持IMNN网络参数一致条件下,将Adam梯度优化算法优化结果与SDG、SGDM、Adagrad[17-19]梯度算法和 BP网络比较。损失函数在迭代300次后的收敛曲线如图5所示。

由图5可以看出,Adam算法的损失函数收敛速度最快,误差精度最小。保持学习率相同前提下,Adagrad梯度算法误差在IMNN迭代到104次时与Adam算法相近,但总体收敛精度大于Adam结果,收敛速度明显比Adam梯度算法慢。各梯度算法学习率见表1。

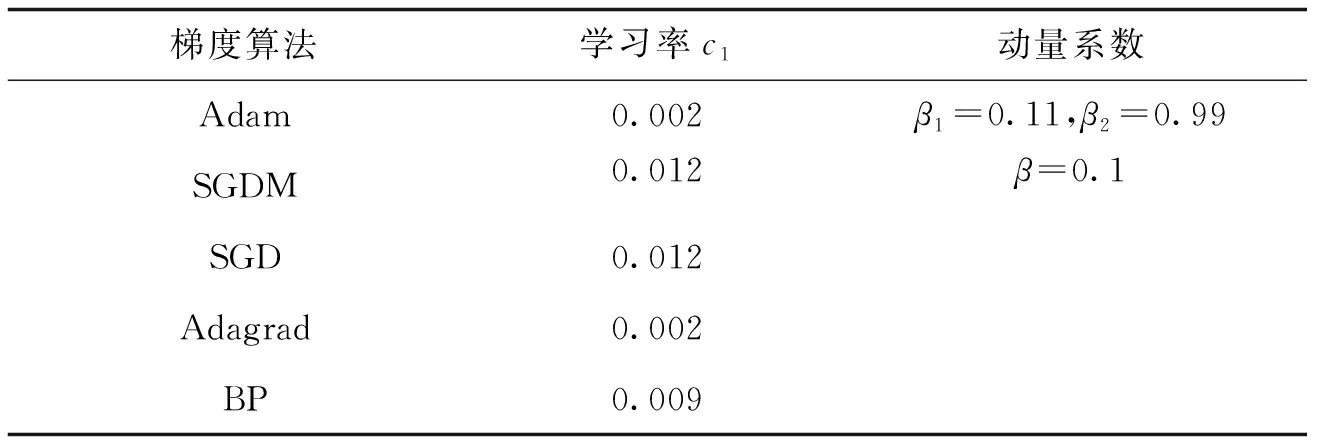
表 1 各梯度算法参数Tab.1 Parameters of different gradient algorithm

为验证粒子群算法优化Adam梯度参数效果,设粒子数目为20,迭代50次,仿真结果如图6所示。由图6可看出,PSO-Adam梯度优化算法的收敛速度及收敛精度都显著提高,优化后PSO-Adam参数设置见表2。

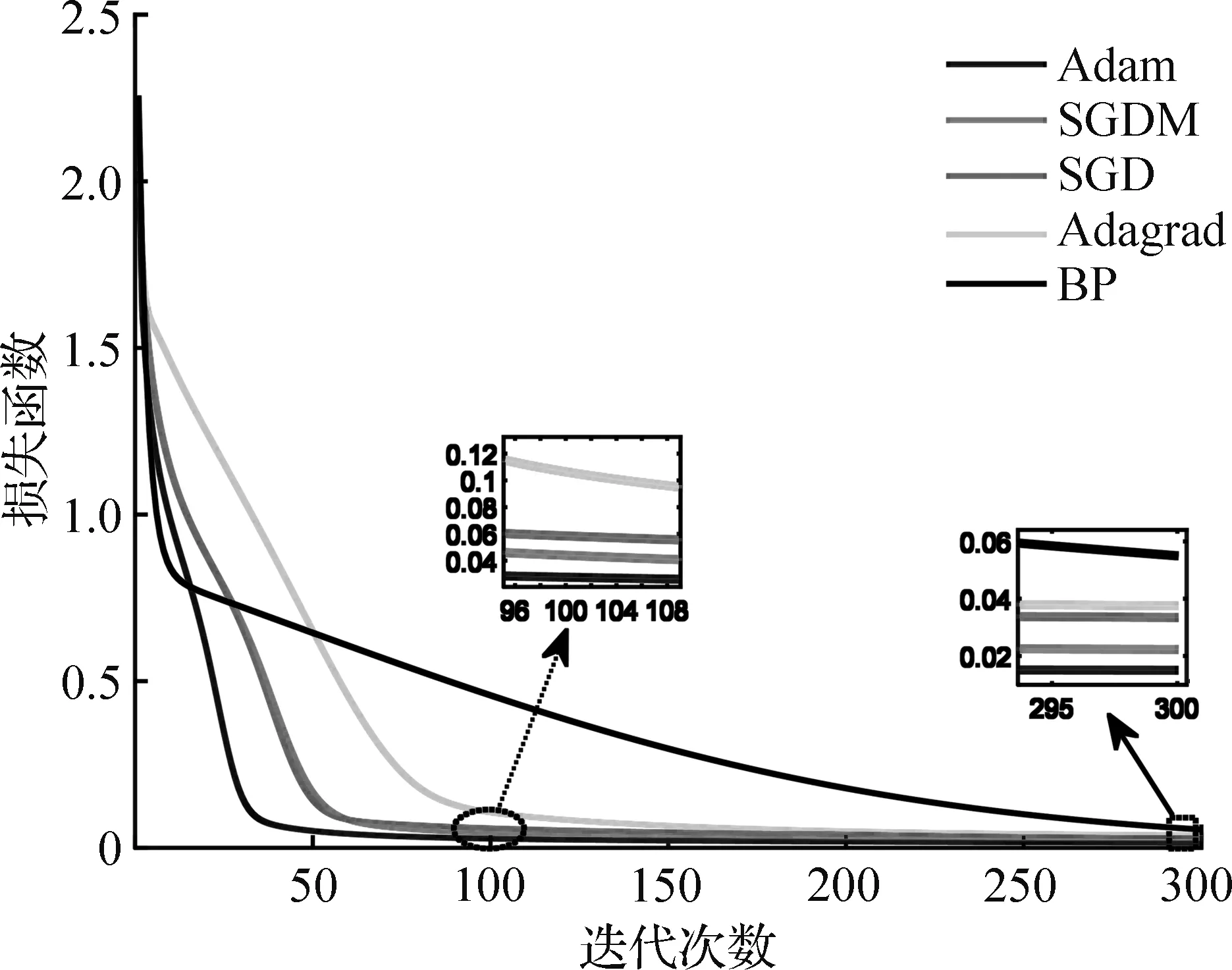
图5 IMNN不同梯度算法收敛速度

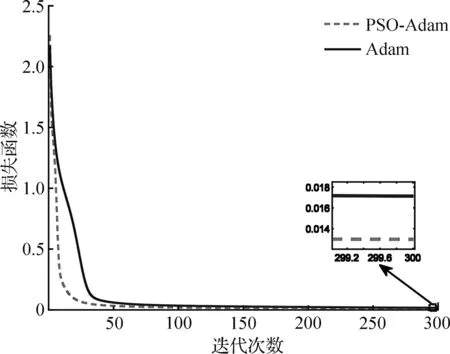
图6 PSO优化Adam参数效果对比

表2 PSO优化参数数据Tab.2 Data of optimized parameters based on PSO

3.2 仿真预测

仿真分析一:取广西某水电站某台轴流转浆水轮机非协联试验获得的153组数据进行仿真,其中水轮机整定水头H=9.3 m。将153组历史数据分为学习集和预测集,学习集为总样本集的80%,其包含输入桨角φⅠ、导叶开度aⅠ和换算水轮机功率输出PⅠ,预测集为总样本集的20%,待预测输入为φⅡ、aⅡ。数据集见表3。

应用IMNN模型对训练集训练,其效果如图7所示,训练值与真实值曲线的高度重合说明IMNN模型训练效果良好并具备预测能力。

学习集样本训练完成后向模型输入预测集,不同反归一化策略方案预测效果如图8所示。

为了进一步验证本文所提出的自适应反归一化区间策略方案,绘制了如图9所示的反归一化策略方案1-3仿真预测效果图,各方案预测数据如表4所示。其中方案3所获得的预测值可视为最理想的情况,即对已知真实值的复现预测值。

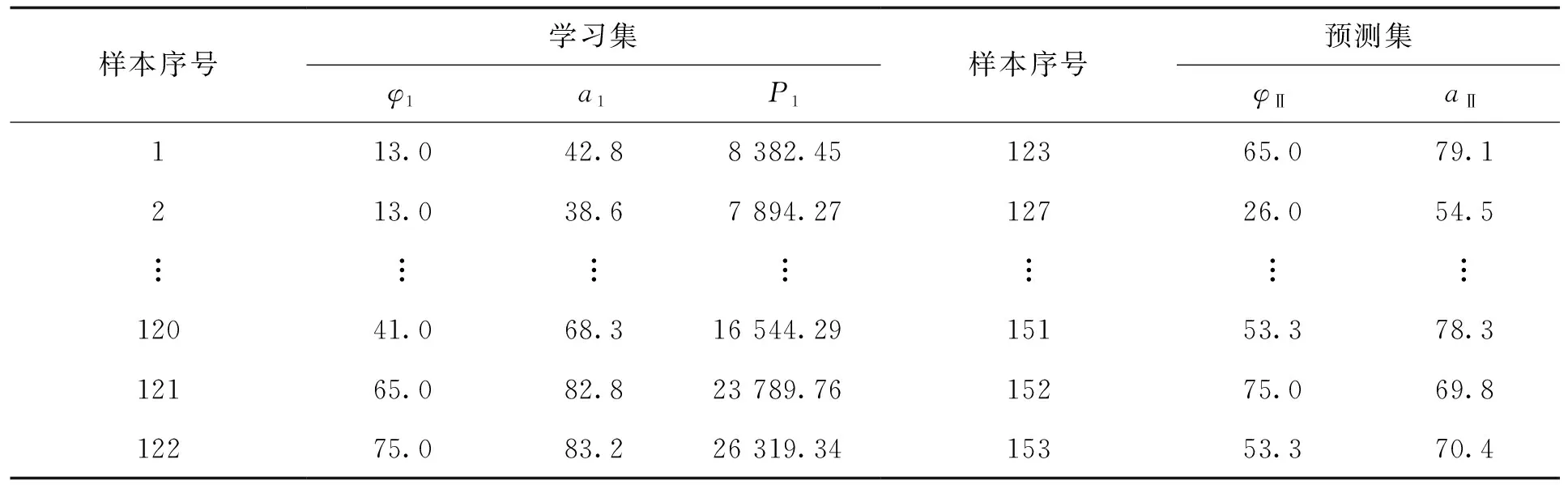
表3 非协联试验学习集与预测集数据Tab.3 Data of learning and prediction with non-coordination test

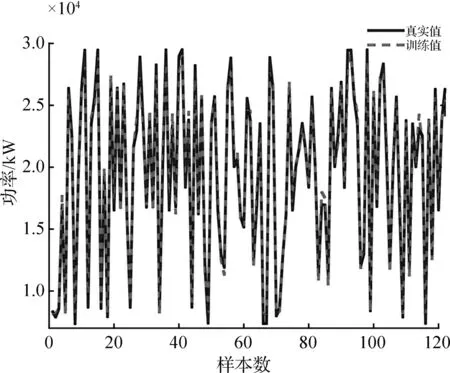
图7 非协联试验IMNN训练效果

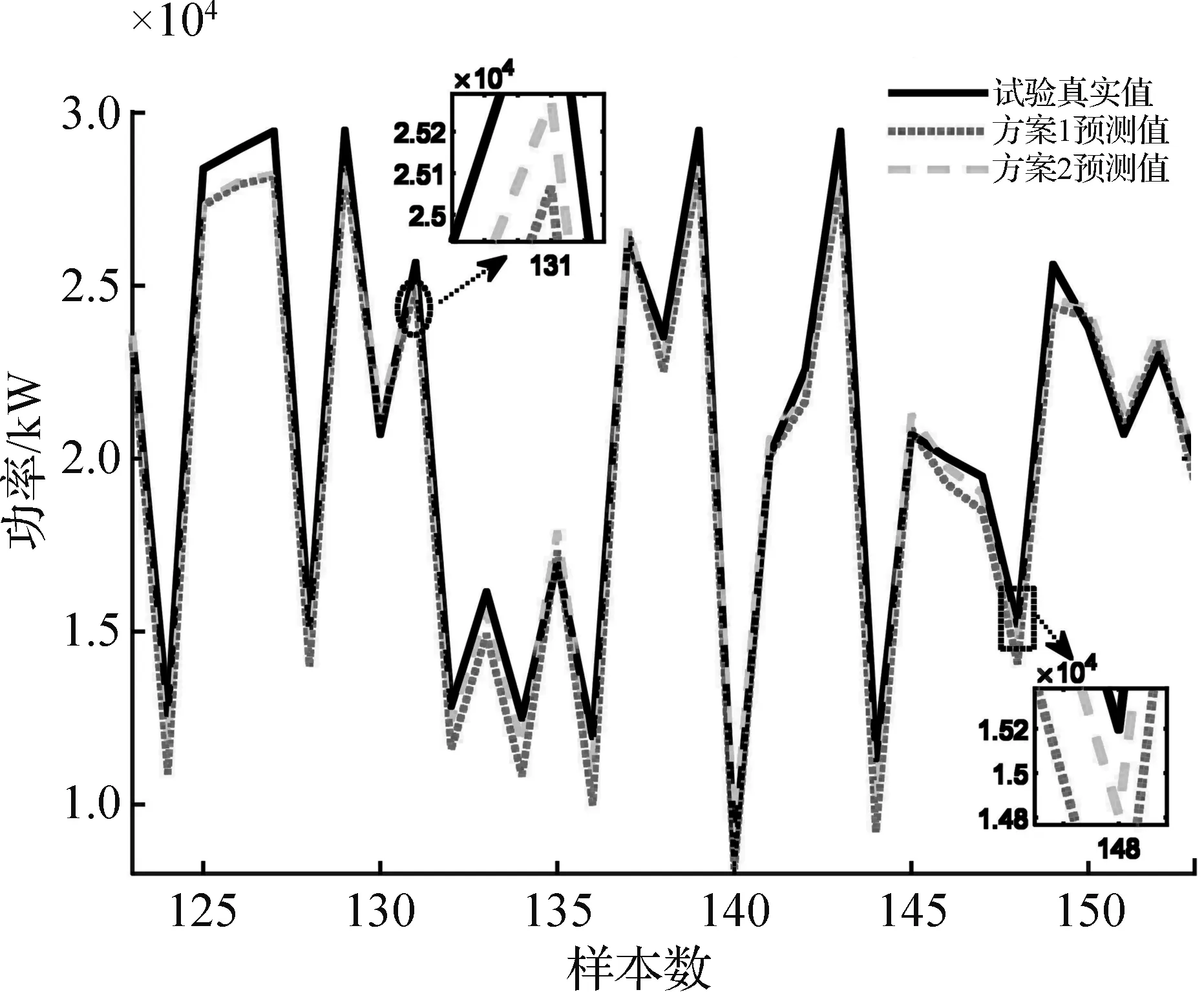
图8 非协联试验IMNN预测效果

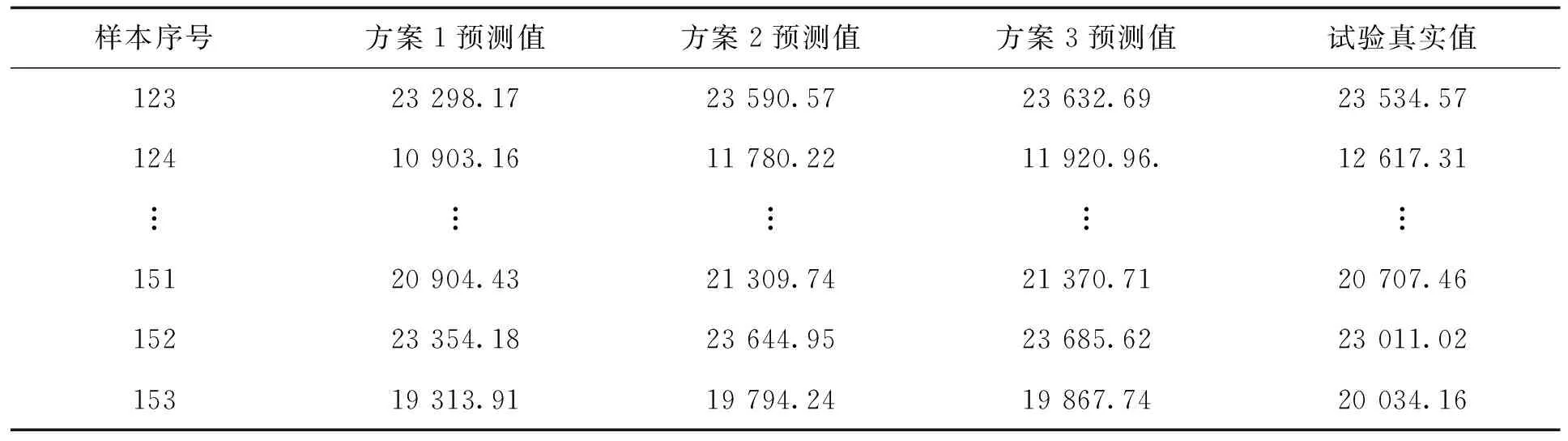
表4 非协联试验预测值与试验真实值数据Tab.4 Prediction data of experiments with non-coordination test

方案3预测值逼近试验真实值线,这是反归一化策略方案3的必然结果。以相对误差,均方根误差(root mean square error, RMSE),平均绝对误差(mean absolute error, MAE)等指标评测预测值与试验真实值的距离。如表5所示的仿真结果表明本文所提出的自适应反归一化区间策略具有对真实值的逼近能力。

表5 非协联试验预测值评测指标Tab.5 Evaluative indicators of predictive value with non-coordination test

仿真分析二:以广西某水电站水轮机协联试验获取的94组协联样本数据为仿真数据,其中整定水头H=6.0 m。协联试验时按照轴流转浆水轮机运行规范协联改变桨叶角度φ、导叶开度a, 在94组协联样本数据中取样本数据集的80%为学习集,预测集取样本数据集的20%,学习集和预测集数据见表6。

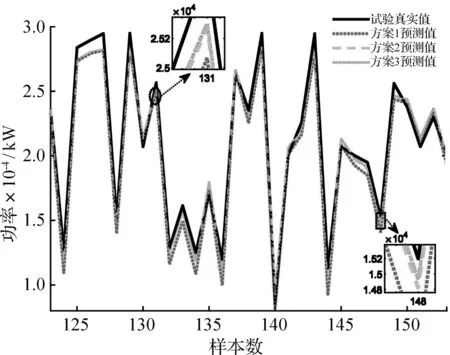
图9 非协联试验预测复现图

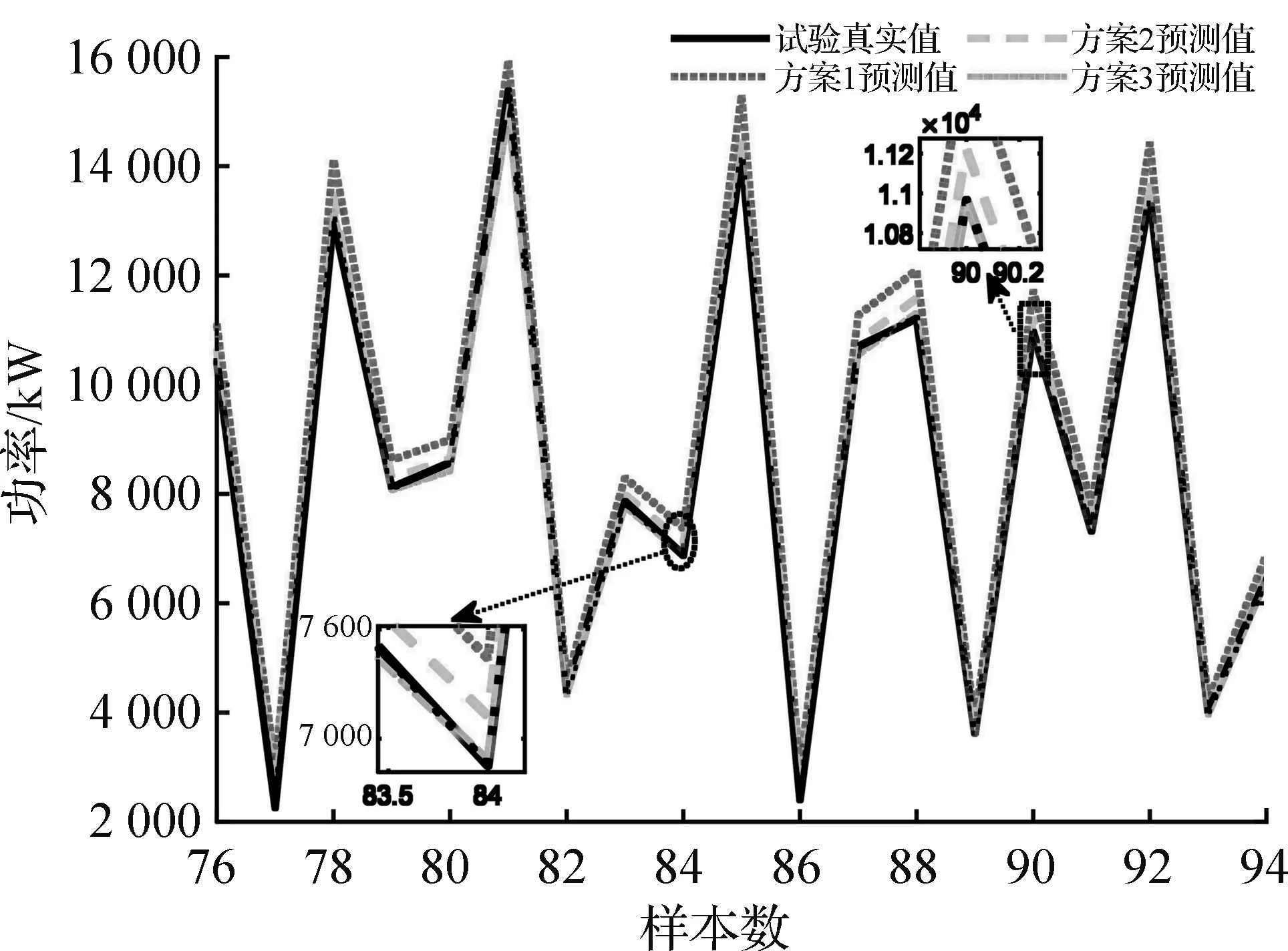
图10 协联试验IMNN预测效果图

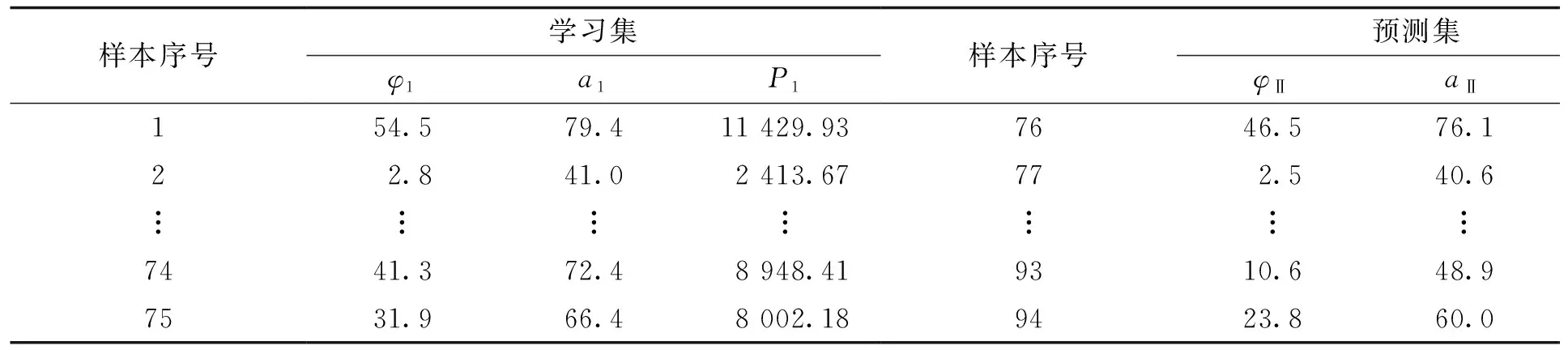
表6 协联试验学习集与预测集数据Tab.6 Data of learning and prediction with coordination test

应用协联数据样本集,经过IMNN训练并进行预测,预测效果结果如图10和表7所示。自适应反归一化预测值(方案2)比方案3预测值效果略差,本质是由于方案3反归一化区间均为真实值,因此其仿真得到的预测值等于真值,方案2预测结果已经最大限度接近真实值,因此自适应反归一化区间策略方案2具有可行性。

协联预测值评测指标见表8。在小样本学习数据情况下,由表8协联预测评测指标结果表明,自适应反归一化预测值仍能逼近试验真实值,具有良好的实际预测效果，进一步证明了所提IMNN模型以及自适应反归一化策略的有效性。

表 7 协联试验预测值与试验真实值数据Tab.7 Prediction data of experiments with coordination test

表8 协联预测值评测指标Tab.8 Evaluative indicators of predictive value with coordination test

4 结论

为了解决水轮机协联试验中数据不足导致的机组运行参数设置问题，本文针对BP神经网络预测模型的梯度下降法收敛速度慢、激活函数在多层网络结构中易造成梯度消失、数据过拟合等问题,提出并推导了改进多层神经网络IMNN的优化过程,根据神经网络实际应用时难以获取预测真实值的区间边界值问题,提出了自适应反归一化区间策略。基于水轮机协联与非协联工况案例分析验证了所搭建的轴流转浆水轮机功率预测模型的准确性和反归一化策略的有效性,模型预测结果可以为科学设置轴流转浆水轮机运行参数提供技术指导。