基于事件触发的分布式优化算法
2022-02-17易新蕾张圣军陈蕊娟李渝哲
杨 涛 徐 磊 易新蕾 张圣军 陈蕊娟 李渝哲
在多智能体系统中,每个智能体(节点)都具有一个局部成本函数,分布式优化的目标是使由局部成本函数之和所构成的全局成本函数最小.分布式优化的研究由来已久,至少可以追溯到[1−2].近年来,由于其在电力系统、机器学习和传感器网络等领域的广泛应用,这一研究重新引起了关注.研究者设计了多种分布式优化算法,详见综述文章[3−10],大致可分为离散时间算法和连续时间算法.
现有的大多数离散时间算法均基于一致性算法和分布式次梯度下降(Distributed gradient descent,DGD)算法[11−15].尽管DGD 算法可以处理非光滑凸函数的分布式优化问题,并在通讯延迟、丢包等多个方向上进行扩展以处理更为实际的情况,但由于使用了衰减步长,因此收敛速度较慢.在步长固定的情况下,虽然DGD 算法收敛速度快,但只能收敛到最小值点的邻域[16−17].最近的研究集中在利用历史信息来设计具有固定步长的加速算法.具体而言,文献[18−19]中提出的算法是基于比例积分(Proportional integral,PI)控制策略,文献[20−25]中提出的算法是基于分布式不精确梯度算法和分布式动态平均梯度跟踪技术[26].现有的连续时间算法可以分为两类:第一类是文献[27−29]中提出的基于梯度的算法,这类算法本质上都是基于PI 控制策略,其中每个智能体使用一个辅助状态(积分反馈)来校正由不同局部梯度引起的误差;第二类算法使用二阶Hessian 信息,例如文献[30−32].
为了避免连续通信和减少通信负担,事件触发通信和控制的思想最初是针对单个系统[33−35]提出的.后来这种思想被应用到分布式一致性问题[36−42].近年来,研究者提出了基于事件触发通信的分布式优化算法[29,43−50].文献[29]提出了一种不存在Zeno行为[51]的事件触发算法,即在有限时间内不会触发无限多次事件,并针对无向连通图,在局部成本函数强凸以及梯度局部Lipschitz 且可微的条件下,证明了算法指数收敛到最小值点的邻域.受文献[30]提出的零梯度和 (Zero-gradient-sum,ZGS)算法的启发,文献[44]提出周期性的事件触发机制;文献[45]则设计了基于动态事件触发的ZGS 算法.针对无向连通图或权平衡强连通的有向图,在局部成本函数强凸且具有局部Lipschitz Hessians 的条件下,证明了算法的指数收敛性.
本文提出了两种基于比例积分策略的分布式优化算法,并证明了算法的收敛性.在此基础上,为了减少通信负担,我们提出了基于事件触发的分布式优化算法,并证明了提出的基于事件触发的优化算法不存在Zeno 行为,且保持了与连续通信下分布式优化算法相同的收敛性.文献[29]提出的事件触发算法只有在局部成本函数强凸且具有局部Lipschitz梯度的条件下收敛到全局最小值点的一个邻域,而我们提出的算法在局部成本函数可微且凸的条件下,即可精确地指数收敛到唯一的全局最小值点.与文献[46]中提出的算法相比,我们提出的算法更简单,因为在执行文献[46]中的算法时需要一些特殊设计的增益参数.与文献[44−45]中提出的基于二阶Hessian 信息的事件触发ZGS 算法相比,我们提出的算法是基于一阶梯度的,易于实现.此外,ZGS 算法需要特殊的初始化,而我们提出的算法允许任意初始化.
本文其余部分安排如下.第1 节介绍图论的基础知识.第2 节介绍本文所考虑的分布式优化问题.第3 节提出两种基于PI 控制策略的分布式优化算法,并分析所提算法的收敛性.第4 节提出基于事件触发通信机制的分布式优化算法并分析其收敛性.第5 节利用数值仿真验证理论结果.第6 节总结本文的主要结果并介绍未来的研究方向.
1 基础概念
在这一部分,我们介绍图论的一些基本知识[52].考虑一个包含N个智能体的无向图G=(V,E,A),其中V={1,2,···,N}表示智能体的集合,E={(i,j):表示边的集合,A=[aij]∈RN×N表示加权邻接矩阵,其中,当 (i,j)∈E时,aij >0 ;当(i,j)∈/E时,aij=0 .在本文中,我们还假设图中没有自环边,即对于所有的i ∈V,aii=0 .智能体i的邻居集合定义为Ni={j ∈V|aij>0}.在无向图中从节点i1到节点ik的路径是指存在节点序列i1,···,ik,使得 (ij,ij+1)∈E,j=1,···,k −1 .
对于无向加权图G,加权Laplacian 矩阵L=的定义是对于,有Lij=−aij,因此,Laplacian 矩阵的行和为零.如果无向加权图G是连通的,则Laplacian 矩阵L有唯一的0 特征值,其对应的右特征向量为1,其他所有特征值均大于零.
符号说明:给定一个矩阵A,AT表示其转置矩阵.对称矩阵A是半正(负)定的当且仅当其所有特征值均为非负(非正)时.给定两个对称矩阵M,N,M ≤N意味着M −N是半负定的.记号A ⊗B表示矩阵A和B之间的Kronecker 积.ρ(·) 代表矩阵的谱半径,ρ2(·) 表示非负矩阵的最小正特征值.In表示维数为n×n的单位矩阵.1n表示n维的列向量,其每个元素都为1.∥·∥表示向量的欧几里德范数或矩阵的诱导2 范数.给定一个向量[a1,···,aN]T∈RN,diag{a1,···,aN}是第i个对角线元素为ai的对角矩阵.对于列向量x1,x2,···,xN,那么由其组成的堆栈列向量用 [x1,x2,···,xN] 表示.
2 问题描述
考虑由N个智能体组成的网络,每个智能体都有一个局部凸函数fi:Rn →R,i ∈V.所有智能体共同协作以找到一个最小值点x∗,使全局成本函数f(x)=最小,即:

智能体之间的通信用无向加权图G=(V,E,A)来描述,其中V={1,2,···,N}是智能体的集合,E ⊆V ×V是边的集合,A是加权邻接矩阵.
如引言部分所述,为了避免智能体之间的连续通信,研究者设计了一些分布式事件触发算法.然而,大多数现有的算法要么需要特殊的初始化,要么只收敛到全局最小值点的一个邻域,这些启发了本文的研究.更具体地说,我们的目标是设计任意初始化的事件触发算法,并精确地收敛到全局最小值点.
我们对局部和全局成本函数作出以下假设:
假设1.对每个i ∈V,局部成本函数fi(x) 是连续可微凸函数.此外,的全局最小值是有界的.
假设2.全局成本函数f(x)=关于全局最小值点x∗是mf-(有限)强凸的,即存在常数mf >0,使得,对任意的x∈Rn成立.
假设3.对于每个i ∈V,局部成本函数fi(x) 具有局部Lipschitz 梯度,即对任意紧集D ⊆Rn,存在常数Mi(D)>0,使得

其中,Mi(D) 称为函数fi(x) 在紧集D上的Lipschitz常数.
在假设1 的条件下,分布式优化问题(1)的全局最小值点x∗可能不唯一.但是,如果假设2 成立,则很容易证明全局最小值点x∗是唯一的.与大多数文献中局部成本函数是强凸的假设相比,这种假设的限制较小.详细讨论,请参见文献[18,46],假设3 在现有文献中也被广泛使用.
3 基于PI 的分布式优化算法
针对问题(1),我们提出两种基于PI 反馈策略的分布式优化算法,其中xi(t)∈Rn表示第i个节点在时刻t对全局最小值点x∗的一个估计,积分项qi(t)∈Rn是用来校正第i个节点由于固定步长所产生的误差.第一种算法如下:


算法(2)的收敛性如下:
定理 1.假设无向图是连通的,并且假设1 成立.如果每个智能体i ∈V运行分布式优化算法(2),则有:
1) 每个xi(t),i ∈V,渐近收敛到全局最小值点x∗;
2) 如果假设2~ 3 也成立,则每个xi(t),i ∈V,以不小于的速率指数收敛到唯一的全局最小值点x∗,其中ϵ2和ϵ3是两个正常数,并在证明中给出.
证明.见附录B.
注 1.算法(2)与文献[27−28]中所提出的分布式优化算法相类似.但是,文献[27−28]只给出了在凸成本函数下,算法渐近收敛的结果.而定理1 给出了在全局成本函数对最小值点有限强凸的附加条件下,算法指数收敛的结果.针对有向图为权平衡强连通的情形,当局部成本函数是可微的凸函数并且具有全局Lipschitz 梯度时,文献[28]中的定理5.4给出了算法渐近收敛的证明.这里我们考虑的是无向连通图,在全局成本函数对全局最小值点是有限强凸的附加条件下,定理1 给出了算法的指数收敛性.
下面,介绍第二种分布式优化算法:

算法(3)的收敛性如下:
定理 2.假设无向图是连通的,并且假设1 成立.如果每个智能体i ∈V运行分布式优化算法(3),则有:
1) 每个xi(t),i ∈V,渐近收敛到全局最小值点x∗;
2) 如果假设2~ 3 也成立,则每个xi(t),i ∈V,指数收敛到唯一的全局最小值点x∗.
证明.该定理的证明与定理1 的证明相类似,这里不再赘述.
注 2.算法(3)与文献[29]中所提出的算法相类似.但是,文献[29]考虑的是局部成本函数强凸的情况,而本文中只要求全局成本函数关于全局最小值点是有限强凸的,是较之更一般的情况.
注 3.算法(2)中xi(0)和qi(0) 均可以任意选择的,而在算法(3)中,虽然xi(0)可以任意选择,但要求因此算法(2)对初始条件qi(0)是更为鲁棒的.然而,与算法(3)相比,式(2b)需要额外通信qj,因此比算法(3)需要更多的通信开销.
4 基于事件触发的分布式PI 优化算法
为了避免智能体之间的连续通信和减少通信负担,将第4 节所提出的分布式PI 算法与事件触发通信相结合,提出了两种分布式事件触发算法并给出其收敛性分析.首先,基于分布式优化算法(2),我们提出第一种事件触发算法,描述如下:

分布式事件触发算法设计中的关键问题是如何构造触发机制,以保证提出的算法不存在Zeno 行为,并收敛到全局最小值点.
定理 3.假设无向图是连通的,并且假设1 成立.如果每个智能体i ∈V运行分布式事件触发算法(4),并通过如下方式确定其触发时间序列:

其中,所有ai,bi,ci,di >0均为设计参数,则有:
1) 算法(4)不存在Zeno 行为;xi(t)i ∈V x∗
2) 每个,,渐近收敛到全局最小值点 ;
3) 如果假设2~ 3 也成立,则每个xi(t),i ∈V,以不小于的速率指数收敛到唯一的全局最小值点x∗,其中ϵ4是正常数,并在证明中给出.
证明.见附录C.
接下来,基于算法(3),我们提出了第二种事件触发算法,描述如下所示:

下面的定理给出了与定理3 类似的结果:
定理 4.假设无向图是连通的,并且假设1 成立.如果每个智能体i ∈V运行分布式事件触发算法(6),并通过如下方式确定其触发时间序列:

其中,ai,bi >0 均为设计参数,则有:
1) 算法(6)不存在Zeno 行为;
2) 每个xi(t),i ∈V,渐近收敛到全局最小值点x∗;
3) 如果假设2~ 3 也成立,则每个xi(t),i ∈V,指数收敛到唯一的全局最小值点x∗.
证明.该定理的证明与定理3 的证明相类似,这里不再赘述.
注 4.基于算法(2)和算法(3),提出了对应的事件触发算法(4)和算法(6).所提出的事件触发通信机制,受到文献[37]中时变触发机制的启发.与算法(6)的触发机制(7)相比,算法(4)的触发机制(5)更为复杂且需要额外通信开销,但是算法(4)的初始条件qi(0) 是可以任意取值的,更为鲁棒.
注 5.文献[29]中定理13 要求所有局部成本函数强凸,而定理3 和定理4 只要求全局成本函数有限强凸,并不要求所有的局部成本函数都如此或强凸.此外,我们提出的算法指数收敛到全局最小值点,而文献[29]中提出的算法只能收敛到全局最小值点的一个邻域.文献[44−45] 提出的事件触发ZGS 算法需要特殊的初始化,而我们提出的算法允许对xi(0) 的任意初始化.
5 仿真实验
考虑一个包含50 个智能体的大规模网络,其中局部成本函数fi具体描述如下:

其中,j=1,2,···,5 .函数fi(x),i=6,···,10,36,···,40,是非强凸的函数,而全局成本函数关于点x∗有限强凸.所有局部成本函数均可微,且具有局部Lipschitz 梯度.随机选取一个包含50 个节点的无向连通图,并针对该网络拓扑图以及上述定义的成本函数得到以下两部分的仿真结果.
不考虑事件触发时,为了更好地体现算法(2),算法(3)与文献[29−31]所提算法的区别,我们对这些算法进行了仿真比较.通过图1 可以看出所有算法均为线性收敛.此外,算法(3)的收敛速度相对较快.

图1 不同算法中的演化Fig.1 The state evolution of in various algorithms
考虑事件触发时,对于算法(4),我们随机选择触发机制(5)中的设计参数ai,bi,ci和di.选择采样周期为 0.01 s.图2 展示了智能体 6,16,26,36,46 的状态演化过程,从中我们可以清楚地看到每个智能体都收敛到全局最小值点x∗=−0.01214 .在[0,40 s]时间段内,上述5 个智能体分别被触发了209,183,161,241,142次.由此可知,事件触发算法(4)在仿真中针对上述5 个节点避免了大约95.32%的通信开销.
对于算法(6),我们随机选择触发机制(7)中的设计参数ai和bi.选择采样周期为 0.01 s.图3 展示了智能体 6,16,26,36,46 的状态演化过程,从中我们可以清楚地看到所有智能体收敛到全局最小值点x∗=−0.01214 .在 [0,40 s] 时间段内,上述5 个智能体分别被触发了 114,121,139,94,182 次.由此可知,事件触发算法(6)在仿真中针对上述5 个节点避免了大约96.75%的通信.与算法(4)所对应的结果相比,智能体被触发的次数更少,因此节省了更多的通信和计算量.

图3 算法(6)中智能体6,16,26,36,46 的状态演化Fig.3 State evolutions of agents 6,16,26,36,46 of Algorithm (6)
6 结论
本文考虑了一类分布式优化问题,针对无向连通图,基于比例积分策略提出了两类分布式优化算法,在局部成本函数为可微凸函数的条件下,证明了所提的分布式优化算法渐近收敛到全局最小值点.当局部成本函数具有局部Lipschitz 梯度,并且全局成本函数对全局最小值点是强凸时,证明了所提算法指数收敛到唯一的全局最小值点.此外,为了避免智能体之间的连续通信和减少通信开销,提出了两种基于事件触发的分布式优化算法.证明了所提出的算法不存在Zeno 行为,并且在相对应条件下保持了与连接通信下分布式优化算法一样的收敛性.未来的一个方向是设计分布式优化算法动态事件触发通信机制的条件.
附录A
下面文献[46]的引理,在后文中指数收敛的证明中起着重要作用.
引理 1.假设无向图是连通的.如果令KN=IN−则有,Laplacian 矩阵L是半正定的,KN1N=0,以及

如下引理是对文献[18]中性质 3.6 的推广,其中每个局部成本函数梯度局部Lipschitz 的假设放松了原有局部成本函数梯度全局Lipschitz 的假设,在接下来的证明中也很有用.
引理 2.假设无向图是连通的,以及假设1~ 3 都成立.那么对任意ε>0 以及任意紧的凸集D ⊆Rn,以及x∗∈D,

证明.对任意x ∈DN,对x=u+v进行分解,且u=和v=x−u.易知,vT(1N ⊗In)=0N.其余证明与文献[18]中性质 3.6 的证明相同,这里不再赘述.□
附录B
定理 1 的证明.1) 在这一部分,我们使用Lyapunov 稳定性分析方法.当假设1成立时,每个xi(t),i ∈V,都渐近收敛到全局最小值点x∗,其可能是不唯一的.方便起见,记符号x=[x1,···,xN],q=[q1,···,qN],以及∇f(x)=[∇f1(x1),···,fN(xN)].则算法(2)可以写为如下紧凑形式:

考虑如下函数:

V1(x,q)沿轨迹(B1)的导数满足:


2) 在这一部分,我们证明当假设2 和3 成立时,算法的指数收敛性.
我们首先证明对于任意的初始状态x(0) 和q(0),存在凸紧集C ⊆Rn,使得x∗∈C和xi(t)∈C,∀t ≥0,∀i ∈V.集合C的具体形式依赖于x(0),q(0) 和x∗,将在后文中给出.
由式(B2)和(B3),对任意t ≥0 和i ∈V,可得:

因此,C={x ∈Rn:||x −x∗∥2≤2V1(x(0),q(0))}是我们要寻找的凸紧集.

类似地,V3(x,q) 沿轨迹(B1)的导数满足:

进而可得,

由于假设1~ 3 成立,由引理2 中式(A2)可得,


考虑如下候选Lyapunov 函数

由(B9)可知,W0(x,q) 沿(B1)的轨迹的导数,满足如下不等式,


附录C

1) 在这一部分中,我们通过反证法证明算法(4)不存在Zeno 行为.假设算法(4)存在Zeno 行为,则存在一个智能体i ∈V,使得,其中T0>0 是一个常数.注意到xi(t) 和qi(t) 都是连续的.因此存在常数P1>0 和P2>0,使得∥xi(t)∥≤P1和∥qi(t)∥≤P2对所有i ∈V和所有t ∈[0,T0] 都成立.
根据假设1 可知f(x) 连续可微,另外∥xi(t)∥≤P1,∀i ∈V,∀t ∈[0,T0].因此,存在一个常数P3>0 使得∥∇f(x)∥≤P3,∀t ∈[0,T0].
令C1=2LiiP1+2LiiP2+P3以及C2=2LiiP1.那么,由式(4)可得,

对于给定的触发机制(5),可得∀t ≥0,


这与式(C3)相矛盾.因此,事件触发算法(4)不存在Zeno行为.

考虑Lyapunov 函数(B2),可得V1(x,q) 沿轨迹(C6)的导数满足:

同时,定义a=max{a1,···,aN,c1,···,cN}>0 .那么由式(5)可得,

由式(B2)可知,

根据式(C8),(C9)和(C10)可得如下不等式

因此

其中

由式(C10)可得,

根据式(C7),(C9)和(C12)可得如下不等式

那么,由式(C13)可知,W1(x,q,z) 沿轨迹(C6)的导数满足如下不等式,

3) 在这一部分,证明当假设2~ 3 成立时,算法的指数收敛性.与定理1中2)的证明相类似.
由式(B2),(C14)和(C15),可得对于所有的t ≥0 和i ∈V,有如下不等式成立:

因此,所要寻找的凸紧集为C={x ∈Rn:||x −x∗∥2≤2W1(x(0),q(0),z(0))}.
接下来,由式(B4)可得V2沿轨迹(C6)的导数满足


其中,第二个等式用到了eq的定义,性质以及引理1 中(A1)给出的性质KNL=L和Cauchy-Schwarz 不等式;第二个不等式利用引理1 中(A1)给出的性质ρ2(L)KN ≤L;最后一个不等式用到了由假设3 得到的f(x)具有局部Lipschitz 梯度的事实.
类似地,由(B15)可得V3沿轨迹(C6)的导数满足

进而可得,

因此,由 ()T[(∇f(x)−∇f())]≥0,式(B8)以及式(C9)和(C16)~ (C17)可得

关于t ≥0 和所有i ∈V,定义ζi(t)=e−bt和ζ(t)=[ζ1(t),···,ζN(t)].考虑如下候选Lyapunov 函数
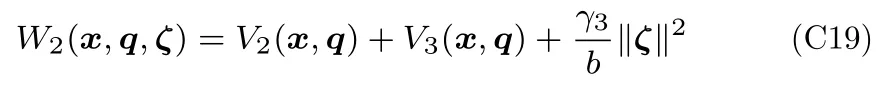
由式(C18)和(C19)可知,W2(x,q,ζ) 沿轨迹(C6)的导数满足如下不等式:

