移动边缘计算网络中基于DQN的能效性卸载决策及无线资源分配

高 云， 郭艳艳， 卫 霞

(山西大学 物理电子工程学院， 山西 太原 030006)

0 引 言

随着通信技术的高速发展， 移动设备有限的计算能力、 存储空间和电池寿命等难以满足复杂移动应用的低时延、 高可靠性需求[1]. 近年来兴起的移动边缘计算(Mobile Edge Computing, MEC)技术能够将移动应用中的计算任务转移到邻近设备的网络边缘， 有效地降低本地服务器的处理压力， 并避免回传和核心网络中的延迟[2]. 然而， 由于通信过程中无线环境的复杂性， 致使计算任务通过无线链路上传到MEC服务器时容易造成无线资源利用率低和丢包等问题. 因此， 如何在保证应用需求的前提下， 找到一种最优的卸载决策和资源分配策略， 具有重要的研究价值.

近年来， 已有许多学者围绕MEC系统中卸载策略和资源优化问题进行了相关研究. 文献[3-5]中， 通过近似最优迭代资源分配算法得到系统能耗最小化的卸载决策和资源分配策略； 文献[6-7]， 为解决移动设备端的任务队列动态数据包卸载问题， 采用李雅普诺夫优化方法获得系统稳定性与长期卸载收益兼顾的卸载策略. 近年来， 深度强化学习(Deep Reinforcement Learning, DRL)被广泛地应用到MEC网络中， 用于解决卸载决策和资源分配问题. 文献[8-10]中， 将发射功率离散化后采用深度Q学习(Deep Q-network, DQN)算法进行功率分配， 而文献[11]中采用深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG)算法解决连续功率变量分配问题. 然而， 现有的MEC卸载决策和资源分配研究中， 在建立优化模型并对相关参数进行联合优化时， 没有考虑这些参数之间的内在联系， 导致优化模型复杂， 实现困难.

针对上述问题， 本文在多种移动设备、 单个移动边缘计算服务器场景下， 考虑计算任务队列稳定和时延限制、 移动设备的最大发射功率限制等条件， 构建以系统长期平均能耗最小化为目标的优化模型. 然后， 将计算任务的卸载决策、 计算资源分配、 上行信道分配和设备发射功率分配的优化问题简化为上行信道和发射功率分配的联合优化问题. 由于信道状态和任务队列变化的马尔可夫属性[12]， 将动态MEC网络中系统平均能耗最小化的问题转化为长期奖励值最大化的问题， 利用DQN算法获取最优的资源分配策略， 进而得到计算任务抵达率与系统能效及数据处理率之间的内在关系.

1 系统模型和问题构建

1.1 系统模型

本文构建的MEC网络模型包括1个MEC服务器、 1个基站及N个不同类型的移动设备. 基站和移动设备均配置单个天线， 且两者之间采用正交频分多址接入方式， 在K个信道进行数据传输， 基站与MEC服务器之间通过光纤连接， 所以忽略它们之间的传输延时. 移动设备的计算任务可以在本地处理， 也可以通过基站卸载到MEC服务器上处理.

Bn(t)=max{Bn(t-1)+Ln(t)-

νn(t)-Dn(t),0}，

(1)

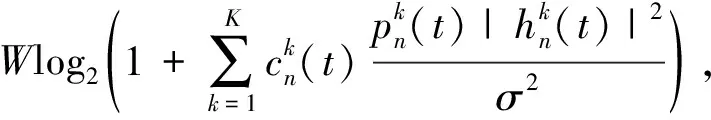
(2)

1.2 系统能耗优化问题构建

MEC系统能耗包括设备本地处理数据能耗、 设备上传数据所需能耗和MEC服务器处理数据能耗. 在时隙t内， 移动设备n本地处理数据的能耗

(3)

式中：ξ1是常数因子， 由移动设备的处理能力决定[13]. 上传数据所需能耗

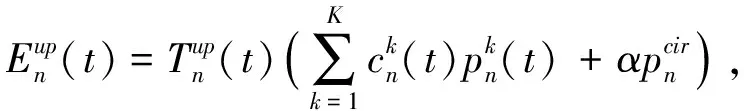
(4)

(5)

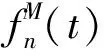
在时隙t内， 系统总能耗为

(6)

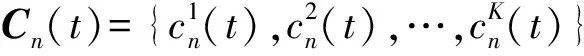
为了最小化系统长期平均能量消耗并保持数据队列稳定， 该系统的优化模型为

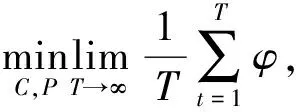
(7)

2 基于DQN的无线资源优化算法

2.1 DQN原理

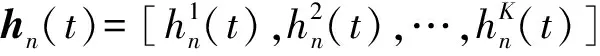
DQN的目标是找到最优的策略， 使长期奖励最大化[16]. 基于当前的状态，s(t)选择动作a(t)=π(s(t))， 得到即时奖励r(t)， 同时状态s(t)转移到下一状态s(t+1)， 再基于新的状态继续与环境进行交互， 持续该过程以得到最大的长期奖励.t时隙累计衰减奖励的表达式为

(8)

式中：E[·]表示均值；λ∈[0,1]为奖励衰减因子. 最优策略π*的表达式为

(9)

在MEC网络中， 数据队列的变化和无线信道的衰落均具有马尔可夫属性. 根据马尔可夫的性质， 下一时刻的状态仅与当前状态相关， 而与之前时刻的状态无关， 所以式(8)以递归方式更新值函数Q， 其表达式为

Q(s(t),a(t))=Q(s(t),a(t))+δ(r(t)+

λmaxQ(s(t+1),a(t+1))-Q(s(t),a(t)))，

(10)

式中：δ为学习率.

2.2 DQN结构

DQN包含两个结构相同的深度神经网络(Deep Neural Network, DNN)， DNN包含一层隐藏层， 两层全连接层. 其中一个DNN为评估Q网络， 用于拟合值函数Q， 其表达式为

Q(s(t),a(t);θ)≈Q*(s(t),a(t))，

(11)

式中：θ为评估Q网络的权重参数. 另一个DNN为目标Q网络， 用于获得目标Q值.目标网络的Q值定义为

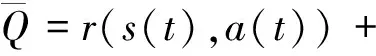
λmaxQ(s(t+1),a(t+1);θ-)，

(12)

式中：θ-为目标Q网络的权重参数.

在学习阶段， 将每次和环境交互得到的奖励与状态更新情况以(s(t),a(t),r(t),s(t+1))的形式存放在经验池中[17]， 当经验池中存储的样本量大于随机抽样的样本量时开始训练.在训练阶段， 从经验池中随机抽取小批样本(si,ai,ri,si+1)， 将si作为评估Q网络的输入， (ri,si+1)作为目标Q网络的输入. 每一步训练中， DQN通过最小化损失函数来更新神经网络的参数， 损失函数的表达式为

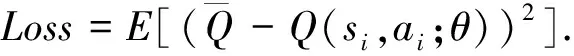
(13)

根据当前从经验池中抽取的样本来计算评估网络参数θ的梯度∇θ， 再使用自适应估计(Adaptive Moment Estimation， Adam)算法更新评估Q网络的参数θ.目标Q网络的参数θ-是通过每隔一段时间将评估Q网络的参数θ直接赋值的方式更新.

3 仿真分析

3.1 仿真参数设置

仿真中主要的环境参数设置见表 1.

表 1 参数配置

神经网络隐藏层数为1， 该层含256个节点， 使用线性整流函数(Rectified Linear Unit， ReLU) 作为非线性激活函数；ε-贪心策略中的ε线性选择从0～0.9； 神经网络的参数更新过程中， 学习率δ为8e-5， 经验池的大小为900， 从经验池中每批次采样128个样本， 学习间隔步长为5， 目标网络参数更新的频率为30. 训练步长为200个回合， 每回合包括500个时隙.

1.2 性能分析

图 1 显示了DQN算法的迭代收敛过程. 在该仿真过程中， 用户数N=5, 从图 1 中可以看出， 该算法在经过30 000多次迭代后逐渐收敛， 证明该算法在保持队列稳定约束条件下合理分配资源是可行的.

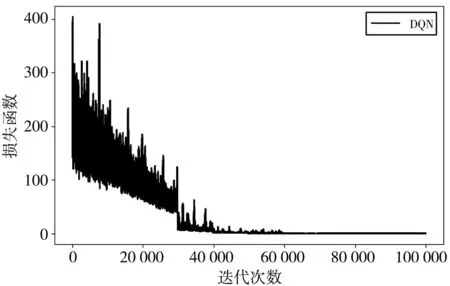
图 1 DQN算法损失函数系Fig.1 The convergence speeds of the DQN algorithm

本文将DQN算法与“本地执行”和“随机选择”算法进行比较. “本地执行”是指计算任务的数据队列只能在设备本地处理； “随机选择”是指计算任务的数据队列随机选择在设备本地处理， 或者MEC端处理. 图 2 描述了计算任务的数据平均抵达率与系统平均能效和数据量处理率之间的关系.

图 2 系统平均能效和数据处理率与平均抵达率关系Fig.2 Average energy-efficiency and packet computingratio against packet arrival ratio

图 3 描述了计算任务的平均抵达率为 1.5 kb/Ts， 系统平均能效和用户数之间的关系. 从图中可以看出， 随着用户数的增加， 3种算法的系统平均能效均在增加， 而本文提出的DQN算法的系统平均能效优于其他两种算法.

图 3 系统平均能效和用户数关系Fig.3 Average energy-efficiency versus the number of users

4 结 论

本文将MEC网络中计算任务的卸载决策及资源分配问题转化为无线信道和功率分配的联合优化问题， 在保证移动设备的计算任务队列稳定和时延限制、 最大发射功率限制等约束条件下， 通过DQN算法实现了使系统平均能耗最小的资源分配策略. 仿真结果表明， 与本地执行和随机选择算法相比， 本文所提出的算法可以有效地提高系统的能效及数据量处理率.