基于Levenberg-Marquardt优化算法的双路电缆温度预测

陆宇升，李 筠，杨海马，刘 瑾，Barkoum Betra Felix

（1.上海理工大学 光电信息与计算机工程学院，上海 200082；2.上海工程技术大学 电子电气工程学院，上海 201600）

0 引言

在常规电缆控温试验中，温度恒定是试验首要任务，电缆电流的变化量是影响电缆温度的主要因素。当电流按一定规律调节时，最终电缆的温度会保持在一个恒定温度附近抖动。如果电缆通过的电流过大，则会导致温度持续升高，造成实际温度超过电缆所能承受的最大值，导致电缆加速老化甚至损坏，严重者会引发火灾等后果[1-3]。因此，预测电缆暂态温度变化对电缆控温试验的安全以及成本控制变得十分重要。

一般地，如果仅考虑暂态过程的电缆温度计算，主要手段是运用有限元法、边界元法、有限容积法等数值计算方法以及仿真分析[4-5]中的公式，通过MGS-LGBM算法[6]以及深度神经网络[7]进行评估。例如文献[8]中通过对电缆各层建立热路模型，再去计算每层的理论温度；文献[9]中用ANSYS有限元软件对电缆中间接头的温度场进行仿真计算；文献中[10]提出用CNN-GRU神经网络对电力系统的负荷数据进行预测。但是在实际试验中，往往求出来的离散暂态温度计算值之间并无直接的联系，这就需要将这些离散值拟合成随时间变化的预测曲线。拟合这些离散数据值的过程就需要用到相关算法和模型函数。如果仅仅计算出这些离散数据点而不分析离散数据点随时间的变化关系，那么在试验预测中这些计算值将变得毫无意义。通过算法拟合后的曲线可以作为预测电缆温度变化的模型。

基于上述分析，本文通过文献[11]中给出的用Runge-Kutta法求解微分方程组的思想来计算电缆暂态温度并得到离散分布的温度值，最后用Levenberg-Marquardt优化算法[12-13]对离散温度值进行非线性拟合，快速得到试验温度的模型曲线，从而极大减少了用传统方式求解预测曲线的计算量；同理可求得第二回路的暂态温度计算曲线。当绘制出的测量曲线偏离预测曲线时，则说明该试验的温度控制存在失控的风险，此时应该及时检查该试验系统的相关参数并评估系统的准确性和安全性，从而避免试验失败以及烧坏电缆的危险；若试验系统的测量曲线大致符合计算曲线模型，则说明试验温度安全可控，从而证明了该计算曲线的预测作用。

1 建立电缆加热等效模型

建立试验电缆的热路等效模型。电缆内部各层结构如图1所示。图1中，1为线芯，是电缆发热的主要部位；2为电缆内部连接管；3是半导体通电区域；4是内绝缘套；5是外绝缘套；6是半导体导电管；7是屏蔽网；8是内保护套；9是外保护套。

图1 单芯电缆结构图Fig.1 Cross sectional structure of single core cable

当电缆线芯通电时，会产生发热量。这是影响电缆温度变化的主要因素，因此可视为电流源W。电缆内部产生的热损耗可分为2部分，一个是电缆内部线芯所产生的发热量，设为热容Q1；另一个是电缆线芯部分到电缆表面之间产生的发热量，设为热容Q2。同时，电缆在发热过程中会产生热阻。热阻的主要来源也可以分为2个部分，其中一个是电缆内部线芯到电缆表面间所产生的热阻R1，另一个是电缆表面到外界环境之间所产生的热阻R2。设电缆的线芯温度为T1，电缆表面温度为T2，外界环境温度为T0。通过电路各元件的关系建立电缆加热简化的等效模型，如图2所示。在忽略电缆线芯的热容和损耗，不考虑绝缘层电阻的情况下，电缆线芯发热量W=kI2，k为发热系数，I2为导体线芯通过的电流。

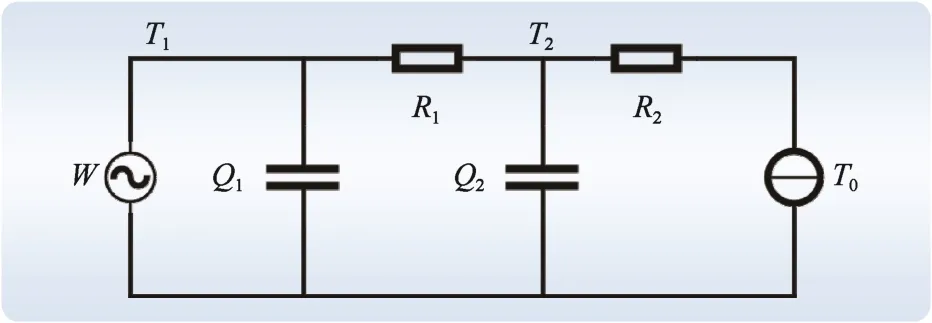
图2 电缆加热等效模型简化图Fig.2 Simplified for heated equivalent model

设在一定时间段t内，只考虑电缆线芯内部电流的变化，根据基尔霍夫电流定律可得加热电缆所对应的热流方程为：

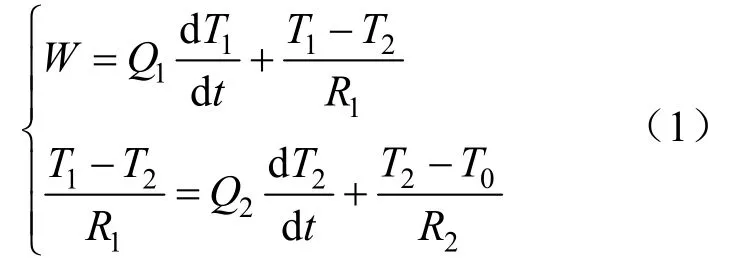
设电缆线芯温度T1=x1，电缆表皮温度T2=x2，电缆温度输出为y，则有：

采用Runge-Kutta法求解公式（2）的微分方程组，得出：

求得电缆温度值为yn=x1n+x2n，则时间与电缆温度值所对应关系可表示为[tn,yn]。

2 基于 Levenberg-Marquardt优化算法求解拟合参数

当计算得出电缆温度的离散值后，需要用该算法对这些温度值进行非线性拟合并生成电缆温度计算曲线模型。通过文献[14-15]可以发现：该算法能够让目标曲线模型对未知参数在其邻域内进行线性近似操作，再通过多次迭代运算得到目标变化曲线函数。

由上节得出n组电缆温度计算数据为，构造函数f(x)=y-x(t)。设参数矩阵为X=[x1,x2,x3,…,xn]T，可构建最小二乘问题：

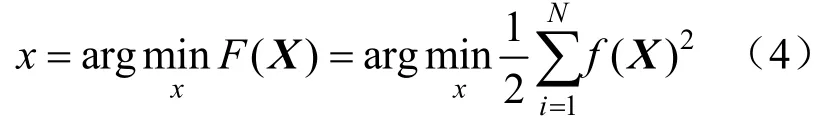
上式中的F(X)为：

将f(X)一阶泰勒展开并去掉高阶项，然后代入到F(X)中得：

对（7）式求h的偏导数并设为0可得：

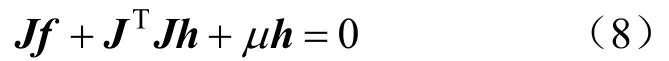
令JTJ=A，Jf=g，则有g=-(A+μI)h。其他情况利用cost增益可以得出：

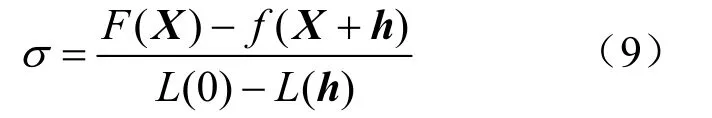
如果满足F′(X)=g(X)=0，且||g∞||＜ε1，则迭代终止；若计算超过最大迭代次数，或者x变化步长距离无穷小，满足||h||=||x2-x1||＜ε2(||x||+ε2)条件，迭代亦终止。

3 试验预测结果及分析

为了满足电缆温度控制试验的需要，开发了双路电缆控温试验系统。该系统可按照IEC标准的要求，对电力电缆进行温度控制试验[16-17]。如图3所示，双路电缆控温试验系统主要用于控制电缆试样导体线芯的电流。该成套系统分别由微机控制台，电气控制箱、微调电源柜、单相感应式调压器、短路变压器、大电流互感器及各种电缆线、连接铜排组成。

图3 双路电缆温控试验系统组成Fig.3 Composition diagram of two-way cable temperature control test system

该系统的输入电压为380 V的交流电，频率为50 Hz；电流互感器调到0～3 000 A的档位，让输出电流在0到3 000 A之间；系统总额定容量为60 kV。对A，B路电缆以及电流互感器分别安装电流传感器。由试验测得，该系统的电流测量精度约为±2%。本试验准备对A路和B路电缆分别加热到92 ℃和90 ℃，并使用二分法调节电流，实现对电缆温度恒定的控制。A、B 2路的主参数设置如表1所示。

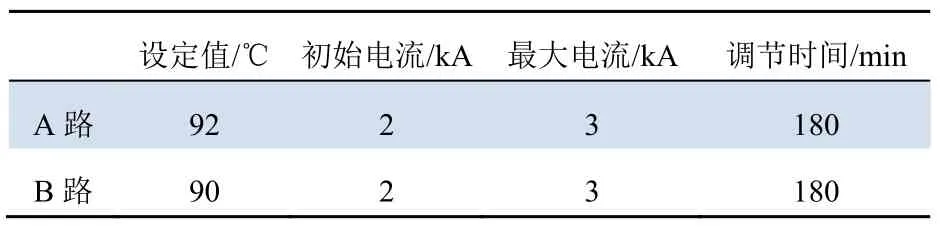
表1 试验主参数设定值Tab.1 Set values of main test parameters

该试验中采用YJLW02 290/500 kV型号的单芯电缆，测温点选择为室外的电缆部分。该型号电缆的物理参数如表2所示。

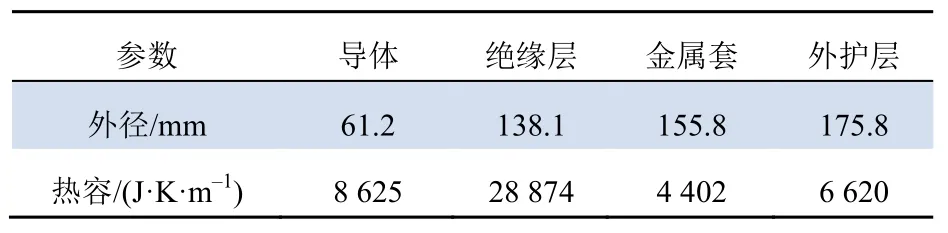
表2 YJLW02 290/500 kV电缆参数Tab.2 YJLW02 290/500 kV parameters

为了维持温度恒定在某一数值附近，必须对电流按一定的规律并依据电缆温度的变化进行不断调节，可使用二分调节法。当温度高于设定值且温度具备上升趋势，此时电流折半递减；当温度小于设定值且温度有上升趋势，或者温度大于设定值但具有下降趋势时，此时电流保持不变；当温度低于设定值且温度有下降趋势时，此时电流折半递增。设实时温度为T，温度设定值为T0，温度的斜率为T′，最小调节电流Ia设置为150 A，最大电流Imax为3 000 A，最小电流Imin为2 000 A，电流调节动态值设为Ik(k≥1,k∈N*)，初始电流值I1为2 000 A，则实时电流调节值Ik+1为：

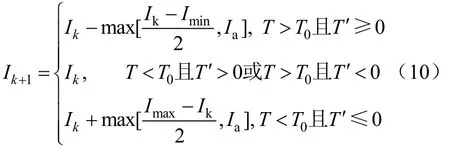
2路电流温度控制同步进行，每路循环一次用时为24 h；整体循环1次，共计时间为48 h。未通电时，电缆的电流值为0。给电缆施加电流，电流以二分调节法的方式升高，电流升高至最大值保持5 h左右时，此时A电缆路电缆达到92 ℃。此后每隔1 min进行一次测量温度记录，调节时间将维持3 h左右，得到A路电缆温度测量值变化曲线。

对于A路电缆计算曲线，需要根据前两节的内容描点并绘图，观察后发现该曲线模型为正弦阻尼，再依据第2节的算法编写拟合程序，得到A路电缆温度计算值曲线。A路温度测量、计算曲线以及电流调节曲线如图4所示。

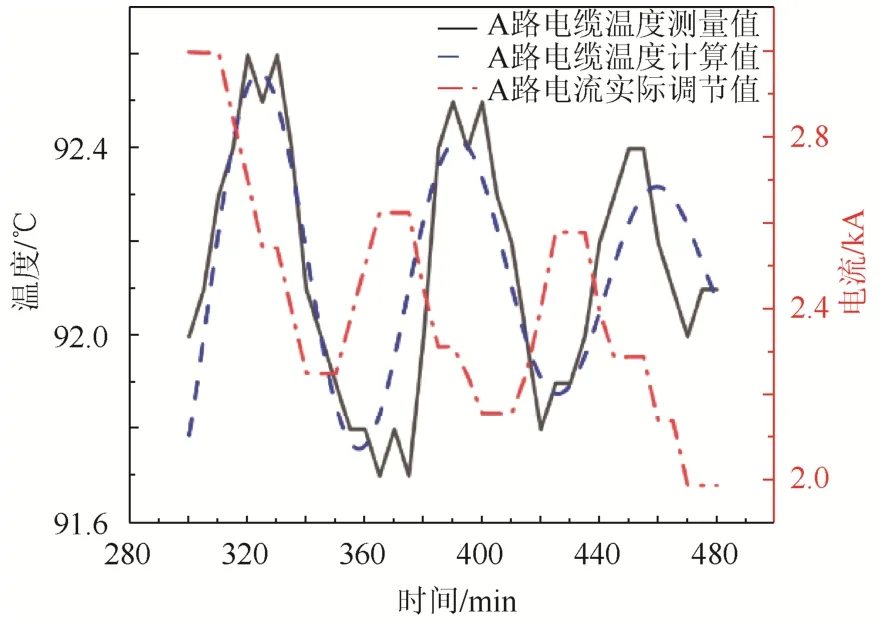
图4 A路温度测量和计算曲线以及电流调节曲线Fig.4 Temperature measurement curve, calculated temperature curve and current regulation curve of circuit A

当进行到8 h时，此时A路温度控制环节结束，进入16 h冷却降温环节；当A路电缆温度恢复到环境温度时，B路电缆控温试验开始。与 A路电缆控温步骤相同，大约进行5 h时，B路电缆升至90 ℃。此后记录数据绘出B路电缆温度测量值变化曲线。对于B路电缆计算曲线，需要根据其电缆温度计算值并进行曲线拟合，得到B路电缆温度计算值曲线。B路温度测量和计算曲线以及电流调节曲线如图5所示。

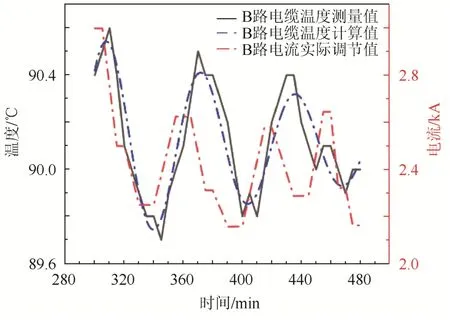
图5 B路温度测量和计算曲线以及电流调节曲线Fig.5 Temperature measurement curve, calculated temperature curve and current regulation curve of circuit B

设A路电缆计算曲线为TA(x)，B路电缆计算曲线为TB(x)，则A路和B路电缆温度计算曲线简化式为：

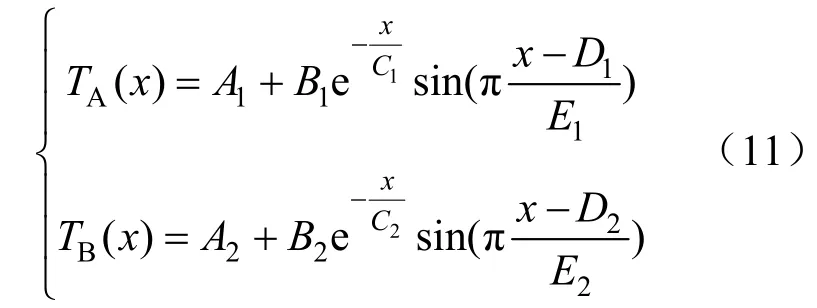
式中：A1=92.12029±0.0235,B1=2.98368±2.4387,C1=169.76314±64.48105,D1=-3 1.59223±8.27248,E1=33.926 24±0.7169；A2=90.10737±0.01529,B2=2.469 74±1.27511,C2=177.387 54±44.9463,D2=-27.788±6.157 75,E2=32.00809±0.500 09（表示方式为：参数=值±标准误差）。

由于正弦阻尼衰减曲线在第一个波峰达到温度上升的最高值，第一个波谷则达到温度下降的最低值；因此预测温度曲线最值的波动范围在第一个波峰处和第一个波谷处取得。设A路预测温度曲线温度上升的最大值为TA1，A路预测温度曲线温度下降的最小值为TA2，A路实际温度上升的最大值为TA′1，A路实际温度下降的最小值为TA′2。对公式（11）中函数TA(x)求导，x定义域为[5,8]。函数TA(x)第一个波峰处在x≈5.396时取得，TA1≈92.562；函数TA(x)第一个波谷处在x≈5.96时取得，TA2≈91.759。在第323 min左右，预测曲线显示会出现上升温度的最大值为92.562 ℃；在第358 min左右，预测曲线显示会出现下降温度的最小值为91.759 ℃。观察图4可以发现，实际温度上升的最大值在第 320 min时出现，上升的最高温度为TA′1约为 92.6 ℃；实际温度下降的最小值在第365 min时出现，下降的最低温度为TA′2约为91.7 ℃。该数据说明A路计算曲线可以在短时间内有效预测到实际温度的最值，从而避免A路电缆温度升高失控的风险。同理也可验证B路预测温度最大值与实际温度最大值之间的关系。试验结果表明，B路计算曲线也能在短时间内有效预测到实际温度的最值。

由图6和图7可以发现，双路电缆温度的绝对误差值大多都在0.2 ℃之内。该结果说明试验系统控温有效且精准，也证明了计算曲线模型能对温度变化趋势进行有效预测，说明了 Levenberg-Marquardt优化算法在温度预测非线性拟合方面应用有效，其极低的误差值满足工程要求。

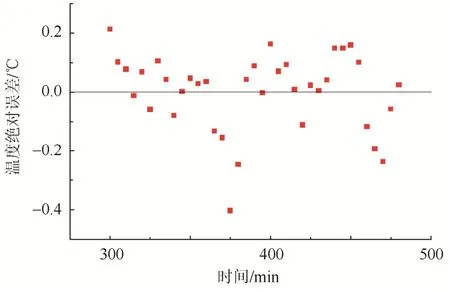
图6 A路电缆绝对误差值分布图Fig.6 Distribution plot of absolute error value of cable circuit A

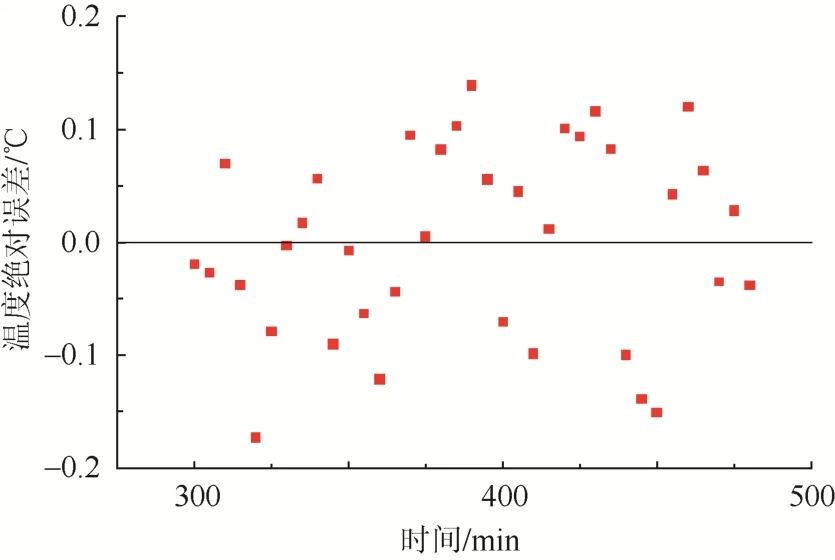
图7 B路电缆绝对误差值分布图Fig.7 Distribution plot of absolute error value of cable circuit B

4 结论

本文通过Levenberg-Marquardt优化算法在调节电流以二分法方式变化的前提下，实现对双路电缆温控试验的温控调节部分进行有效预测，将暂态温度的离散计算值通过该算法拟合得出完整的计算曲线。该方法相较于经典数值方式有如下优点：

（1）当电缆电流快速下降时，电缆温度并未立刻响应降温，这说明电缆温度变化具有迟滞性。引入二分法后发现响应变快，这说明了二分算法的有效性和精准性。

（2）通过 Levenberg-Marquardt优化算法对离散计算值进行非线性拟合，可以有效建立双路电缆温度计算曲线模型，从而解决了用传统数值方式直接求解温度变化曲线的难题。

本文所述的电缆暂态温度预测方法还存在一些不足。在通过Levenberg-Marquardt优化算法建立电缆温度计算曲线模型之前，还需要对相关时间点的温度用Runge-Kutta法进行手动计算。若离散计算值分布杂乱无规律，则此时使用Levenberg-Marquardt优化算法可能不会准确建立电缆温度计算曲线模型。由于电缆所试验条件的局限，该算法针对极端环境下的电缆温度预测的有效性需要进一步试验并验证。