基于SVM 的低空飞行冲突探测改进模型
2022-02-17王尔申宋远上佟刚王传云曲萍萍徐嵩
王尔申,宋远上,佟刚,王传云,曲萍萍,徐嵩
(1.沈阳航空航天大学 电子信息工程学院,沈阳 110136;2.沈阳航空航天大学 辽宁通用航空研究院,沈阳 110136;3.沈阳航空航天大学 人工智能学院,沈阳 110136)
通用航空产业是中国经济新常态下重要的经济增长点[1]。随着中国低空空域的逐步开放,低空空域中通航飞行器数量的增加,增大了彼此发生飞行冲突的可能性。低空空域原则上是指真高(地高度)1 000 m(含)以下空域[2]。为保障通航飞行器在低空空域的飞行安全,对飞行冲突探测技术开展深入研究是有必要的。飞行冲突探测与解脱是研究飞行器在未来一段时间内是否发生潜在冲突并对此潜在冲突建议规避碰撞飞行轨迹的过程,而准确的冲突探测是规避碰撞的前提。
受到复杂而多变的地形、建筑物及气象条件等多种因素的影响,在低空空域内,多飞行器的飞行呈现复杂的相互制约性使得产生飞行冲突的概率增加,传统的航路航线冲突探测算法在特定低空空域内存在局限性[3]。空中飞行器的飞行速度较快,因此要求飞行冲突探测过程在短时间内完成,并保证稳定性和可靠性。
飞行冲突探测主要分为几何法与概率法[4]。文献[5]将冲突的概率转化为对应于某一时刻的冲突区域与联合航迹误差的交叉体积的积分,但没有确定冲突类型。文献[6]对冲突类型进行了数学描述,给出了确定冲突类型的方法。但是,受到天气、环境、人为操作的误差等因素的影响,飞行器之间不是严格的几何关系,计算结果有较大误差。概率型冲突探测方法考虑飞行数据的误差,具有容错性优点[7]。概率法主要使用概率流理论、马尔可夫链、博弈论、复杂网络等方法[8-10],该类方法的准确度依赖于阈值与参数的选择,较为复杂。运用几何法研制的第二代交通防撞系统(TCASⅡ)能对装有该系统的飞机发送警告,不适用于未加装该系统的通航飞行器。广播式自动相关监视广播(ADS-B)技术为空中交通管理能力提升提供服务[11],利用ADS-B信息,文献[12]研究采用粒子群与支持向量机(SVM)算法得到飞行冲突概率模型,但计算复杂。
结合航迹预测,基于4D航迹的飞行器飞行动力模型可预测飞行器的位置[13],从而判断飞行器之间是否存在飞行冲突。但由于通航飞行器飞行具有较强的机动性,该方法不适用于通航飞行器。利用意图信息来推测航迹的冲突段[14]。通过飞行器的时空棱柱计算飞行器的冲突情况,但该方法适用于飞行员与管制员之间的提前协调。
为解决以上冲突探测模型不能适用于形状各异及参数多样化的通航飞行器的问题,保障通航飞行器在低空空域内的安全飞行,本文采用考虑到飞行器形状的保护区模型作为冲突区域。为减少冲突探测模型中的复杂度,采用改进后的ID3决策树算法与随机森林(RF)减少分类器的复杂度,为解决该冲突探测模型中的sigmoid函数存在的容易饱和的问题,采用适应度更好、更敏感的tanh函数进行概率映射。
1 数据预处理与保护区
离群点是指在导航设备接收到的数据中,不符合数据一般特性或者运动模型的数据。用DBSCAN(density-based spatial clustering of applications with noise)高分辨率的聚类算法,去除飞行数据中的离群点。
1.1 离群点处理
设第i个飞行器的航迹集Qi=(V1,V2,…,Vm)表示m个航迹点的集合,其中Vk={xlat,xlon,xalt,xv,xr}表示第k个航迹点的具体信息,依次包括经度、纬度、高度、速度与航向信息。将聚类处理后的数据归一化处理,设2个飞行器在t时刻的位置信息分别为Va={xlat1,xlon1,xalt1,xv1,xr1}与Vb={xlat2,xlon2,xalt2,xv2,xr2},利用位置信息得到2个飞行器的相对距离d,水平方向上的相对速率Δv=xv1-xv2,依据飞行数据中的航向角,计算出垂直方向上的相对速度Δvt,飞行器的相对航向角Δr=xr1-xr2,其中航向角以正北为0°,正东为90°,将样本空间的特征量设为(Δr,d,Δv,Δvt,t)。
1.2 保护区模型
由于存在系统误差及无法消除误差的情况,飞行器的探测容易受到外界因素的干扰。故采用以飞行器为中心建立椭球体保护区。目标飞行器为有保护区的飞行器。
椭球体的保护区用公式可以表示为

式中:(x1,y1,z1)表示飞行冲突的飞行器坐标;(xo,yo,zo)为椭圆中心飞行器的位置;n、m、k分别表示x、y、z三个半轴的焦距。
依据《民用航空空中交通管理规则》[15],为简化飞行器的保护区模型,设置椭球体的长焦距(水平焦距)为n1=m1=1 000 m,短焦距(垂直焦距)为k1=150 m。保护区模型如图1所示。
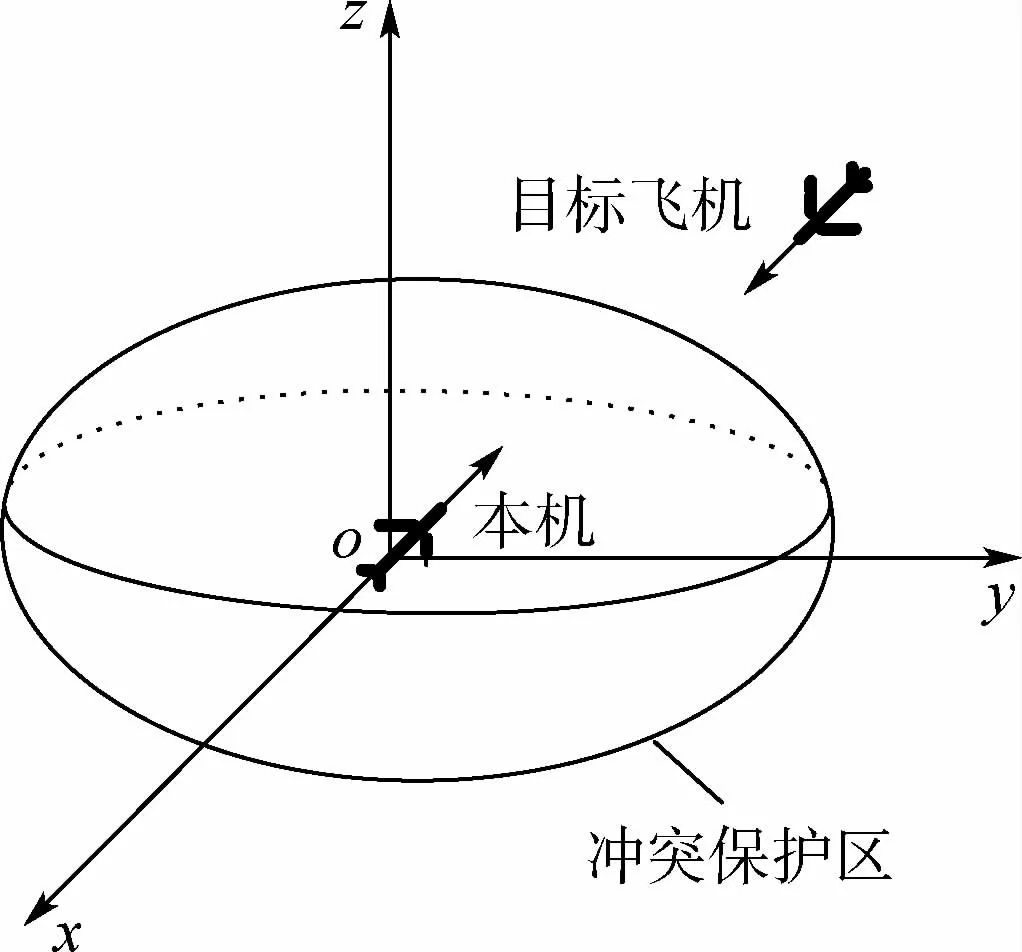
图1 保护区模型Fig.1 Protection zone model
2 SVM 模块
SVM是按监督学习方式对数据进行二元分类的广义线性分类器,其决策边界是对学习样本求解的最大边距超平面。核函数将飞行数据映射到高维空间中进行分类。
2.1 SVM 分类原理与径向核函数
常见的核函数有二次核函数、多项式核函数、径向基核函数(radial basis function,RBF)和多层感知机核函数。在同样的样本情况下,飞行数据的特征维度较低、样本中的标签较少、样本数量较多的情况下,高斯径向基核函数的分类效果较好,分类界限更准确,因此高斯径向基核函数的拟合度较好。故在此分类中,采用RBF。RBF函数作核函数,表达式为

式中:σ决定数据映射到新的特征空间分布,σ越大,支持向量越少,σ值越小,支持向量越多。
假设飞行器的位置、速度、航向角等数据构成的集合A={D1,D2,…,Dn}没有被一个超平面错误分开,求解广义最优分类超平面转化为

式中:w为权重向量;b为偏置量;αj为松弛变量;Dj为输入;C为惩戒因子,调节优化方向中2个指标(间隔大小和分类准确度)偏好的权重;针对错误分类的样本,Uj为训练样本,j为训练样本的个数,使用惩戒因子进行惩罚。
使用决策函数h(x)获得标准的硬输出。

支持向量的个数影响训练与预测速度,为选择最优的σ与C,采用GA-PSO优化方法[16]。在GA-PSO方法中,利用遗传算法(GA)机理对粒子进行变异,增大粒子群优化(PSO)算法中粒子的不确定度,从而增强全局搜索能力。
2.2 tanh函数优化概率输出
通过决策函数,比较h(x)值与0的大小,用输出值的大小判断风险的等级,常用sigmoid函数把SVM将分类结果输出映射到[0,1]区间,带有优化的sigmoid函数表达式为

由于sigmoid函数容易饱和,采用tanh函数优化概率输出,tanh是机器学习中的激活函数,输出区间为[-1,-1]。在数学中,tanh为双曲正切,表达式为
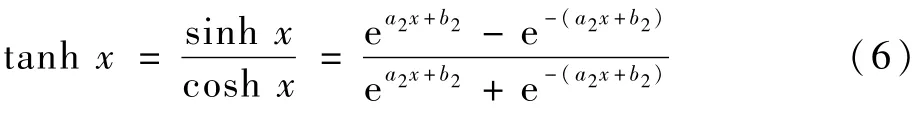
式中:x为SVM 的输出结果;a2、b2为优化参数,利用最小化训练数据与极大似然函数可以求得优化参数;tanh x为输出概率优化表达式。
图2为sigmoid和tanh函数比较结果。由图2的结果可知,sigmoid在输入处于[-6,6]之间时,函数值变化敏感,一旦接近或者超出区间就失去敏感性,处于饱和状态,影响神经网络预测精度。tanh的输出和输入能够保持非线性单调上升和下降关系,容错性好,有界,渐近于0和1,符合飞行冲突探测中冲突概率变化规律。但由于tanh函数输出区间为[-1,1],由于飞行冲突概率不存在负概率,采用输出区间[0,1]的部分。

图2 sigmoid与tanh函数的比较Fig.2 Comparison of sigmoid and tanh function
3 基于SVM 的飞行冲突探测改进
由于RBF函数在将飞行数据映射到高维度的空间和分类的过程中存在计算量大的问题,在大量的飞行航迹数据中,预先找到最有可能产生冲突的飞行航迹,可有效降低RBF函数分类过程中及飞行冲突探测过程中的复杂度。
3.1 改进的ID3决策树算法
决策树是一种将样本的搜索空间分为若干个子集再进行搜索的方法,具体如下:
设样本数据集为X,类别数为n,设第i个数据样本为Ti,X中总样本为,则样本属于第i类的概率为

式中:Ci表示类别。
对决策树划分Ti的信息熵为
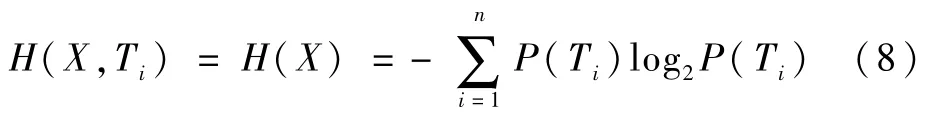
若选择属性a3进行测试,其信息熵为

则属性a对于分类提供的信息量为

式中:I(X,a)表示属性作为分类属性后信息熵下降的程度,即信息增益。选择使得I(X,a)最大的属性作为分类属性,得到决策树的确定性最大。
改进的ID3决策树算法具体步骤如下:
步骤1数据的归一化处理、伸缩性处理。将训练集的样本数据分为若干个子集合,每个单独的子集组成新的决策树。
步骤2选出具有全部样本X的、规律为W的子集X1(W称为窗口规模,X1称为窗口)。
步骤3当I(X,a)=H(X)-H(X|a)最大时,选取每次测试的属性,形成当前窗口的决策树。
步骤4将每个子集得到的分类规则组合,得到一个分类规则。
步骤5顺序扫描子集类内的所有样本数据,如果存在不符合当前分类规则的样本,则进行步骤4,如果不存在,则算法结束。
改进后的分类方法具有全局性良好、抗噪声性强、易于选取训练集等特点。
3.2 改进的冲突探测模型
在SVM 算法中,当训练集较大时,训练所需的时间及空间复杂度分别为O(n2)与O(n3),n为训练集的数量,因此,需要准确取训练集。RF是一种为分类器设计的组合方法,采用RF为SVM算法提供训练集的组合。
改进后的探测模型在飞行前封装成固定的模块,将需要预测冲突的飞行器参数特征量作为输入,获得相应的冲突判断与冲突概率输出。为提高分类结果的准确率,对该模型产生虚报、误报的测试集与训练集进行剔除,提高该探测模型的准确度。改进模型的具体步骤如下:
步骤1对第i个飞行器的m个航迹归一化处理后,使用DBSCAN算法去除离群点,得到预处理后的航迹集合。
步骤2将预处理后飞行器之间4个特征量D=(d,Δv,Δr,t),利用RF选取适合的组合作为训练集合训练SVM分类器。
步骤3将预处理后的样本X,利用改进ID3决策树算法选择具有飞行冲突的飞行器集合Vm=(Va,Vb,…,Vx)。
步骤4重复步骤3,直到没有新的元素出现在集合Vm中。
步骤5将具有飞行冲突飞行器的集合Vm加入已经训练的SVM分类器,得到分类输出集合Wm=(y1,y2,…,ym)。
步骤6将步骤5得到的集合Wm用tanh函数映射到[0,1],得到飞行冲突概率。
步骤7将得到的结果,去除产生虚报和误报的数据,组成特征量训练集,训练SVM分类器。
4 实验验证与结果分析
为了验证本文算法的性能,以辽宁通用航空研究院研制的RX1E型号飞行器为例,其翼展较长,翼展的长度不能忽略,不能将其看作质心。锐翔RX1E通航飞行器参数如表1所示。

表1 锐翔RX1E通航飞行器参数Table 1 Par ameters of RX1E general aircraft
为保证飞行人员安全,在飞行器实际飞行数据中没有具有冲突的情况,故采用模拟双机飞行的方法验证,即一个飞行器为实际飞行器,设置一个与实际飞行器存在或不存在飞行冲突的仿真飞行器,从而实现模拟双机飞行,记录模拟双机飞行的飞行数据。根据飞行航迹与保护区模型判断飞行器在速度、高度、水平方向上是否存在飞行冲突,从而获得类别标签,同时获得σ与C、a与b的值。实际飞行器的数据为锐翔RX1E飞行器于2019年11月14日在沈阳法库财湖机场飞行数据。根据飞行航迹与保护区模型,对飞行器在速度、高度、水平方向上是否存在飞行冲突进行验证。
4.1 水平冲突验证与分析
在飞行数据中设置水平方向上的飞行冲突,即航线冲突。探测2个飞行器在0~100 s之间的距离与飞行冲突概率的变化情况,样本容量为100个,时间步长为t=1 s,相对航向角≤90°,为交叉航向角,将研究的改进模型与SVM算法进行对比,2个飞行器的距离与飞行冲突概率如图3所示。为分析tanh函数与sigmoid函数在飞行冲突探测过程对分类结果的映射效果,将水平方向上的飞行冲突分类结果用sigmoid函数和tanh函数进行映射,sigmoid函数和tanh函数的比较如图3所示。
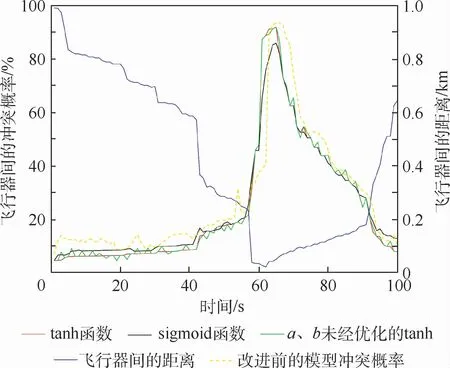
图3 水平冲突概率变化值曲线与映射函数曲线Fig.3 Horizontal conflict probability curve and mapping function curve
由于sigmoid函数对一定的输入范围敏感,使得在0~25 s与95~100 s的较低概率区间与62~73 s的较高概率区间的输出趋于饱和。tanh函数具有更敏感的输入空间,使得在高概率输出区间与低概率输出空间都具有灵敏性,经过优化的tanh函数曲线结果更加准确。
由图3可知,改进后的探测模型给出的飞行冲突概率曲线与飞行器间的距离变化一致。在21~23 s与45~47 s内,飞行器之间处于距离持续减小阶段,改进后的探测模型在该阶段给出的冲突概率具有更好的稳定性。与SVM 算法不同的是,改进后的探测模型给出的冲突概率不受在t=26 s时刻出现的异常点的干扰。在t=61 s时刻,两飞行器的距离处于最低点,改进后的探测模型在t=62 s时给出了最高的冲突风险概率,而SVM算法在t=63 s时达到最高的冲突风险概率。
4.2 高度冲突验证与分析
样本容量为100个,时间步长t=1 s。由图4可知,改进后的探测模型给出的飞行冲突概率曲线与飞行器之间的距离变化一致,在108~118 s与140 s~159 s内,改进后的探测模型得到的飞行冲突概率变化曲线更稳定。在t=159 s时刻,飞行器之间相距最近,改进后的探测模型给出的冲突概率也在t=159 s时刻达到最大,而SVM算法在t=160 s时刻给出最大冲突概率,该探测模型的性能更好。

图4 高度冲突概率结果Fig.4 Vertical conflict probability results
4.3 速度冲突验证与分析
在同一高度,以具有冲突的同向运动的两飞行器作为研究对象,其中一个飞行器匀速运动,另一个飞行器非匀速运动。探测2个飞行器在0~100 s之间的相对速率与飞行冲突概率的变化情况。样本容量为100个,设置时间步长为t=1 s。仿真结果如图5所示,在0~42 s内,2个飞行器之间的相对速率减小阶段,改进后的探测模型在该阶段的冲突概率稳定减少,具有更好的稳定性。在42~93 s内,2个飞行器之间处于相对速率增加阶段,改进后的探测模型在该阶段给出的冲突概率处于稳定增加,具有更好的稳定性。与SVM算法不同,改进后的探测模型给出的冲突概率未受到t=23 s时刻出现的异常点的干扰,在t=42 s时刻给出了最低的冲突风险概率,而SVM算法在t=44 s时刻达到最高的冲突风险概率。
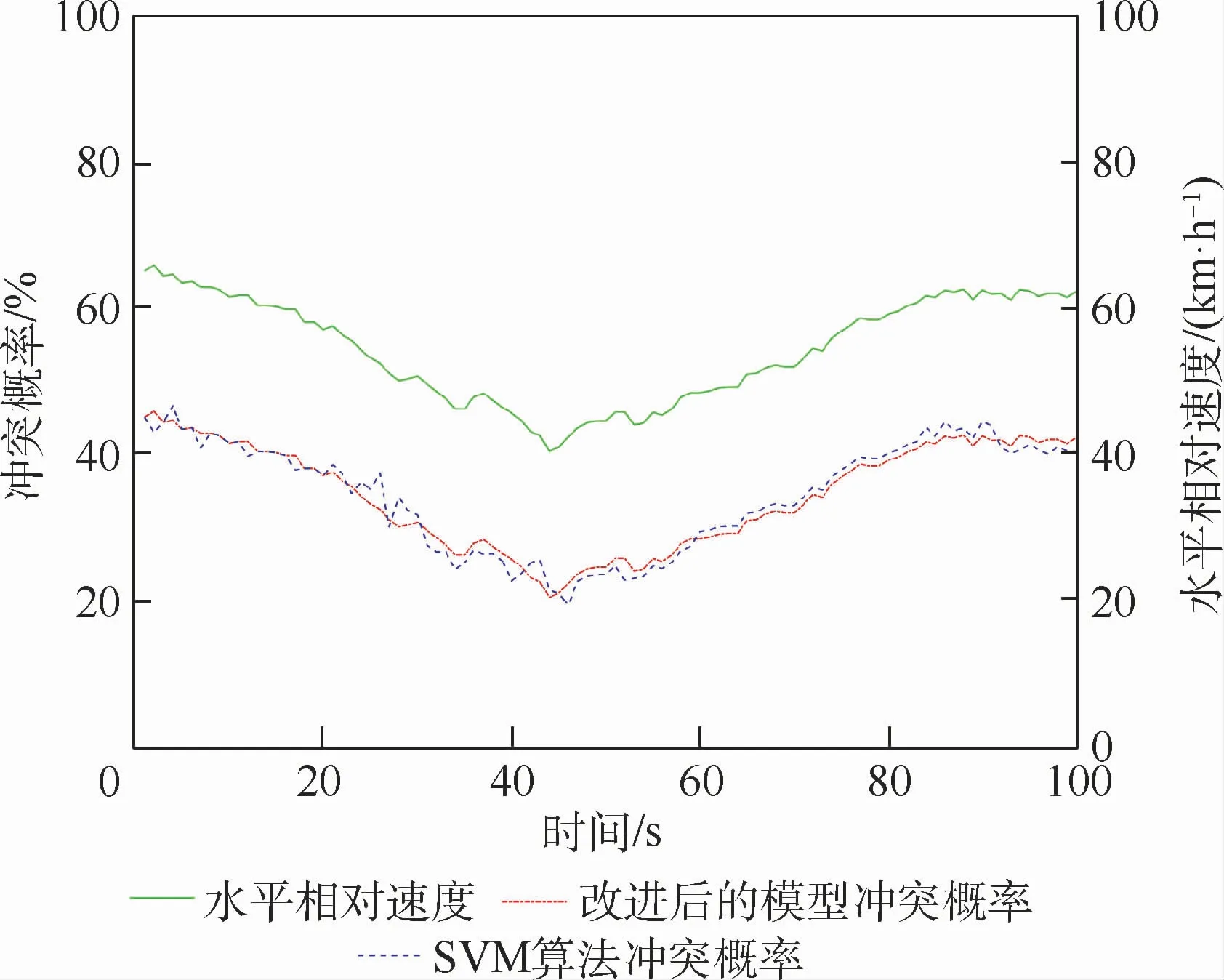
图5 水平方向上相对速度冲突的概率变化曲线Fig.5 Probability curves of horizontal velocity conflict
在不同的高度以具有冲突的同向运动的2个飞行器作为研究对象,一个飞行器匀速运动,另一个飞行器非匀速运动,探测2个飞行器在0~100 s的垂直相对速度与飞行冲突概率的情况。样本容量为100个,时间步长为t=1 s,结果如图6所示。
由图6看出,在0~4 s内,SVM 算法给出的冲突概率是先增加后减少,改进后的探测模型在该阶段给出的冲突概率处于稳定增加,具有更好的稳定性。在22~38 s内,SVM算法给出的冲突概率是带有波动的增加,改进后的探测模型在该阶段给出的冲突概率处于稳定增加,具有更好的稳定性。

图6 垂直方向上相对速度冲突的概率变化曲线Fig.6 Probability curves of vertical velocity conflict
4.4 冲突探测模型实时性与准确性分析
为获取训练样本,模拟300次双机飞行,记录飞行器飞行特征量,作为SVM 的训练集,并根据飞机航迹与保护区模型判断是否存在飞行冲突。每个飞行器的每个属性的样本容量为1 000个,将具有飞行冲突的飞行器作为研究对象,利用飞行器的飞行数据来验证算法的准确度与复杂度,其中算法时间、误报率与虚报率取300次模拟运行结果的平均值,结果如表2所示。
由表2可以看出,在相同条件下,相较于其他2种方法,改进后的探测模型降低了飞行冲突探测误报率与虚报率,所运行的时间分别减少了0.21 s与0.49 s。

表2 三种探测方法的准确率比较Table 2 Comparison of accuracy among three detection methods
5 结论
本文中提出了一种基于SVM 的飞行冲突探测改进模型。主要有以下改进:
1)采用椭球体保护区,降低了数据的误差对冲突过程中的干扰,采用DBSCAN聚类算法、优化训练集的方法减小了SVM算法的误差。
2)利用RF、决策树、降低数据维度的方法,减小了SVM算法的复杂度。
3)相较于SVM 算法,改进后的模型的误报率与虚报率较低,算法运行时间较少,而且具有较好的抗干扰能力和稳定性。
