基于VMC仿生四足机器狗步态设计
2022-02-17周晨魏文新杨喜全
周晨,魏文新,杨喜全
(大连海事大学,辽宁大连,116026)
1 研究背景
随着社会的发展,科技的进步,机器人作为一个朝阳产业,其正在不断地被应用到各个领域当中[1]。不同运动方式的机器人有着不同的优点,其中四足机器人是利用了仿生学和人工智能,通过机械设计得到得复合体。它的仿生结构有着天然的优越性,可以模拟四足动物的运动形式来适应不同的地形环境,在未来有着广阔的发展前景[2]。
2 四足步态
我们将足式动物的运动模式定义为“步态”,步态就是指足式动物各腿之间的固定相位关系。不同的的四足动物因身体结构的差异,运动的步态也呈现出不同的形式,我们以四足狗的运动状态为例,分析三种常见的步态[3-5]。
2.1 crawl步态
crawl步态是四足动物在慢速行走的状态下,任意时刻都有三条腿处于支撑相,一条腿处于摆动相,每次都是一条腿抬起,然后按照左前,右后,右前,左后的次序轮换的向前摆动,如图1.1所示。我们定义四足每条腿与地面接触的的时间和一个完整步态周期时间的比值为占空比β,一个完整的的步态周期为T,定义Ts,Tm分别为支撑相周长和摆动相的周期,则β=Ts/T当占空比0.75 ≤β<1时,任意时刻均有至少三条腿处于支撑相,由于是规则步态,所以一个周期的运动规律相同且各腿之间的相位差:
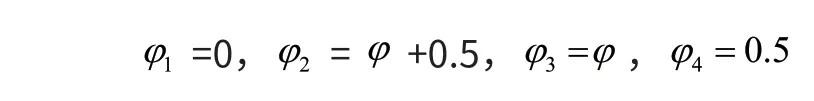
我们一般取crawl步态的临界状态β=0.75且φ= 0.25,任意时刻仅有三条腿作为支撑相,这样四足机器狗形进的速度加快,不会出现停顿感,时序如图1所示。
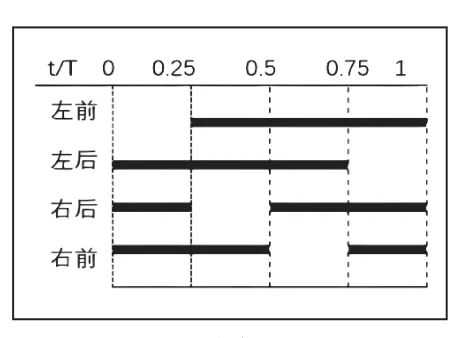
图1 crawl时序
2.2 trot步态
trot步态是小跑步态,由于该步态调速范围大,运动稳定性高且具有较高的能量效率,使得trot步态成为最常见的四足步态,其特点是两拍步态,任何时刻仅有对角的两条腿完成摆动和支撑运动。由于trot步态也是规则步态,其各腿的相位差为:
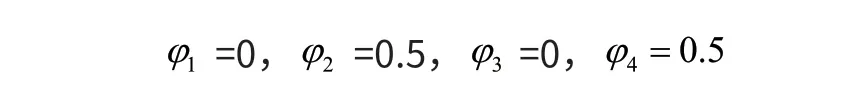
假设取β>0.5时会出现四足全部为支撑相的情况,此时可以对四足的平衡姿态进行调整,但是这样会使运动出现停顿,速度无法达到期望值,则我们可以选取占空比=0.5(如图所示),这样四足机器人的对脚可以直接由摆动相转变为支撑相,依次交替摆动实现平衡和速度的最优化,时序如图2所示。
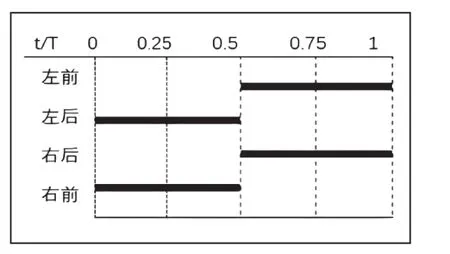
图2 trot时序
2.3 其他步态
pace步态为溜蹄步态,其特点是相同侧的两条腿同时运动,左侧前后腿为摆动相的同时时右侧腿为支撑相,这种步态常见于狗在安全的环境下放松的运动的场景中,该步态相位差为:
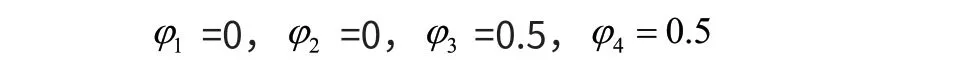
以β=0.5为例,此时pace步态不会出现四足全部触地和腾空的现象,任意时刻只有一侧为支撑相或摆动相,这种步态平衡性比较差速度也受到了限制,所以一般不常用[6]。
3 足端轨迹规划
足端轨迹规划是四足腿部控制达到目标点的前提,根据目标的位置来确定轨迹的函数方程中的变量,然后进一步通过方程求出足端坐标,将得到的以时间为函数变化的坐标通过运动学的逆解得出四足关节转动所需要的角度,通过循环程序实现周期性的运动,从而精确的实现腿部的运动学控制。
为了实现理想的步态模型,足端轨迹规划必须满足形进时平稳,关节部位没有交大的冲击且摆动相抬腿和落地时实现零冲击且足端轨迹圆滑。时刻足端处于摆动项,~T时刻足端处于支撑相。水平方向为X,竖直方向为Z,S为步频,H为离地高度,Tm为摆动相时间,T是步态完整时间,其在X方向和Z方向的条件约束为:
(1)水平X方向
(2)竖直Z方向
(3)在约束条件下的复合摆线摆动相轨迹函数如下
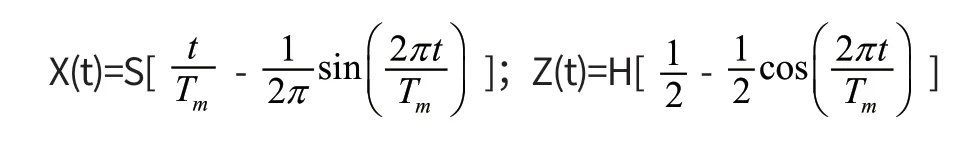
由于该轨迹的方程在t=0和t=Tm时刻加速度会出现跳变,导致接触与抬腿时产生较大的力,这与我们的要求相违背,于是我们采用优化的摆线轨迹方程,令其加速度函数为:
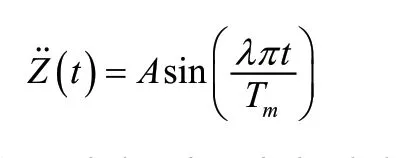
再对其求积分得到速度函数,根据速度的约束条件得到的方程再对速度函数积分得到位移函数,根据位移的约束条件将其用分段函数表达:
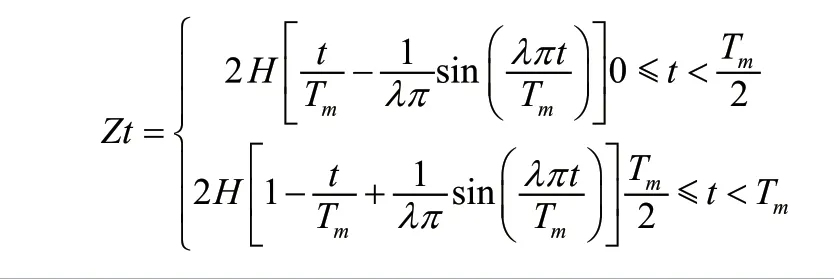
图3 足端轨迹方程
这里的λ的取值关系到关系到Z轴方向上的速度变化,λ值越大速度变化就更频繁,通过matlab仿真得出,取λ=4时轨迹是最平滑的,通过对轨迹方程我们可以得到一个冲击较小且平滑的曲线。
4 分解式虚拟模型步态算法
4.1 VMC支撑相控制算法
VMC算法其实是一种力控算法,其核心就是利用假想的弹簧阻尼构件连接机器人的内部作用点和外部的期望点,通过连接点之间的虚拟力来引导机器人实现目标运动,这些虚拟力通过jacobian矩阵计算得到期望的关节力矩作为电机的控制输入,全局空间下的作用力转换为关节力矩,二者的映射关系就是雅可比矩阵。要想求取雅可比矩阵首先要根据机器人的腿部获取其正运动学模x型,我们定义xn为n个自由度的的位姿向量,qm是m个关节变量的位置向量,得到:x=f(q),然后求x对q的偏导得到:
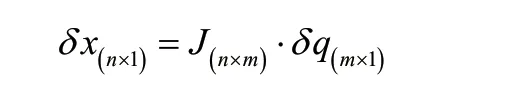
得到了jacobian矩阵J(n×m),将关节的速度映射成足端的移动速度。虚拟功可以表示为:
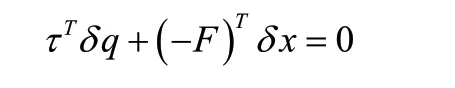
其中,τ为关节力矩向量,F为外部作用力,就可以得到外部作用力和关节力矩的关系:
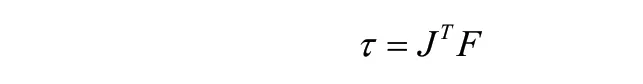
上述方法在单腿支撑相中的应用如下:
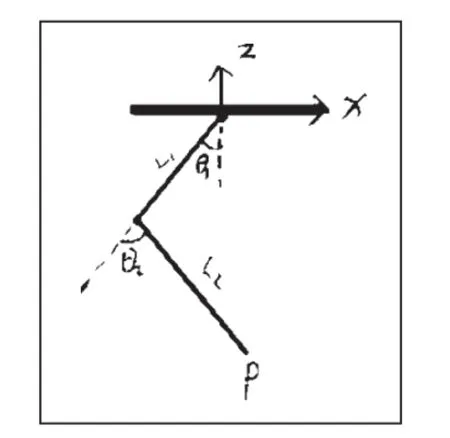
图4
当四足机器人在单腿支撑时我们可以得到其正运动学的的关系式:
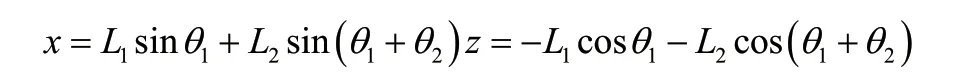
对各关节求偏导数得到jacobian矩阵为:
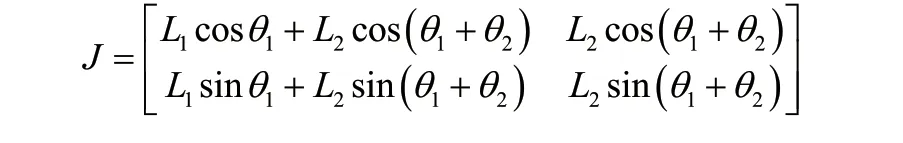
大腿部的力作用在足端。所以支持相的控制法则为:
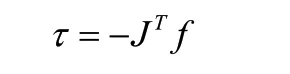
施加在足端的虚拟构件产生的虚拟力为:
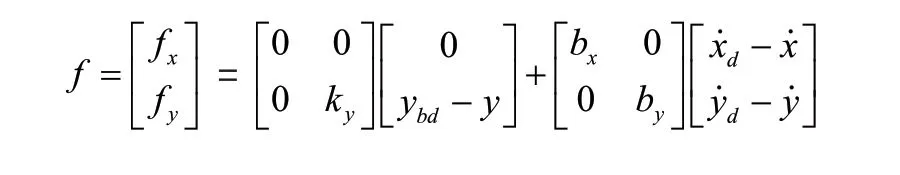
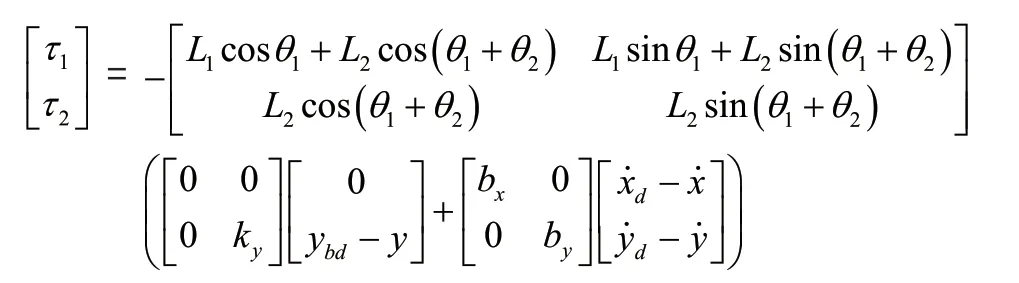
4.2 VMC摆动相控制算法
摆动相的控制方法有两种首先我们这里采用之前提到的复合摆线足端轨迹然后将此轨迹通过运动学的逆解之后得到关节运动轨迹,这样的方式能够得到比位置控制方法更高的精度,并且能精准的到达预定的抬腿高度和落脚点。
运动学正解是已经知道运动关节的各个电机运动参数,也就是此时对于初始位置转动的角度,去求末端执行器的相对参考坐标系的位姿。而运动学逆解恰恰相反,是根据相对参考坐标系的位姿去求出运动关节的各个电机此时对于初始位置转动的角度,通过几何方法解出大腿和小腿的舵机转动角度θ1和θ2,然后将计算出来的角度值输出至舵机运动库中,从而实现死四足的运动。
第二种方法是VMC摆动相控制通过足端虚拟的弹簧阻尼力来牵引足端沿着目标轨迹进行运动的一种控制方法,其在二维空间中可以分解为x轴与y轴方向的力。
其施加在足端的虚拟力为:
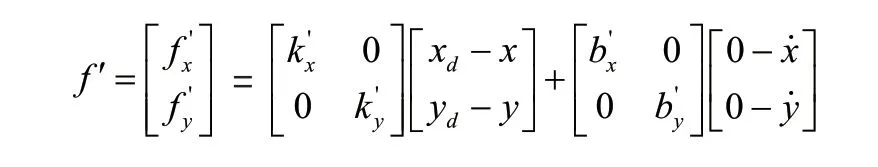
根据支撑项所求的单腿Jacobian 矩阵可以得到关节力矩即:τ,合并公式得出摆动相VMC力矩方程:
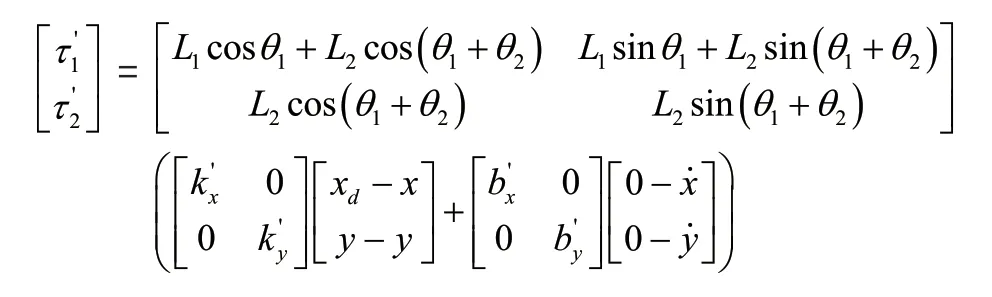
这种力矩控制更加接近于仿生学,并不需要对运动学逆解进行求解,在一定程度上减少了运算量并且提高了控制效率。
5 运动控制仿真分析
5.1 仿真环境及仿真模型
为了实现分解式VMC方法在四足机器人上的应用,本节会制作相关仿真程序,并根据VMC控制方法,使用Matlab对一个空间立体四足机器人模型进行Trot匀速小跑仿真。
本篇文章使用Matlab进行步态仿真试验,基于Simulink仿真环境来搭建四足机器人运动学模型。在 soldwork中建模,设计合适的构件比例,把.urdf文件后导入Matlab中,再补充四足机器人中的动力学参数,将各构件设置为匀质量构件,目的使其质心位于各构件的几何中心,设立坐标轴。通过3D模块设置关节驱动,添加关节角度传感器,得到完整的四足机器人运动仿真模型。
图5 仿真模型
5.2 Vmc单腿轨迹规划
利用Matlab简易搭建Vmc单腿仿真模型,编写腿部VMC控制程序,模拟机器人trot步态。
摆动相memory模块记录上时刻位置值,其中插入积分模块,对摆动相进行计时实现以周期的腿部摆动往复运动。通过机器人腿部位置的捕捉,同时我们通过Matlab绘制出预期x-z平面下的足端轨迹图并和返回的足端位置曲线进行对比。
为测试小腿部分我们在坐标系中绘制单腿在步态周期内的运动状态图。仿真稳定时,可以发现步态运动曲线基本符合期望轨迹,可以看到髋部坐标系下腿的高度期望值Zd=0.5m,但是就是不能够达到,他的影响因素有很多,其中占主要作用的是我们在计算雅各比矩阵是没有消除掉惯性力的作用,另外腿部关节的摩擦力,也使得抬腿高度不能跟随虚拟力达到期望位置。
搭建四足机器人的simulik仿真模型,将上述得到的单腿轨迹规划,对应到机器人四条腿,设置相位差,使得四条腿能交替进行支撑相与摆动相,实现trot步态。

图6 单腿仿真
可以从图中观察到四足机器人四条腿可以实现摆动相和支撑相的交替运动,实现稳定trot步态,用示波器来显示仿真过程中z轴方向上足端运动曲线。
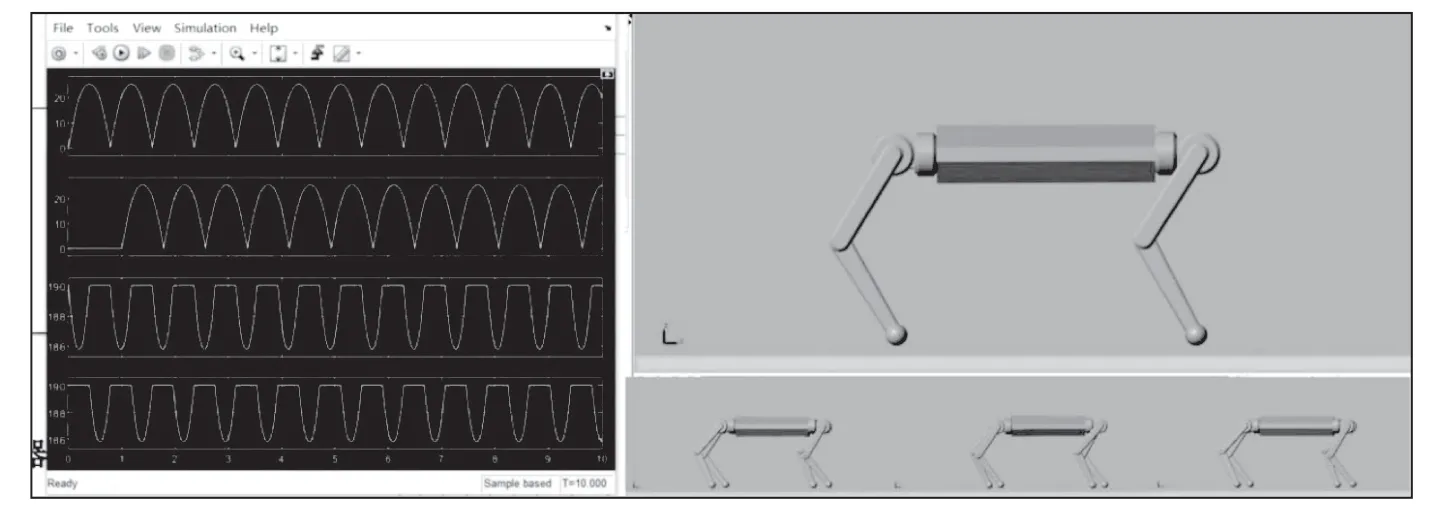
图7 四足trot步态
6 结束语
本次项目完整的实现了四足机器人从设计到实现的全过程,并且通过实物验证了理论的可行性[7-10],但是目前的程序设计和理论无法达到在复杂地形的平稳运动,且在运动关节上采用的舵机为运动控制输出,相比于无刷和行星减速机等动力输出原件还有很大不足,后期努力实现四足机器人在复杂地形的平稳运动。
