基于优化初始聚类中心的Kmeans聚类算法
2022-02-17郭文娟




摘 要:针对传统的Kmeans算法运行的结果依赖于初始的聚类数目和聚类中心,本文提出了一种基于优化初始聚类中心的Kmeans算法。该算法通过量化样本间距离和聚类的紧密性来确定聚类数目K值;根据数据集的分布特征来选取相距较远的数据作为初始聚类中心,避免了传统Kmeans算法的聚类数目和聚类中心的随机选取。UCI机器学习数据库数据集的实验证明,本文所提出的改进的聚类算法获得了良好的聚类效果,同时获得较高的聚类准确率。
关键词:聚类;Kmeans聚类;聚类数目;初始聚类中心
文献标识码:A
在模式识别、数据挖掘和机器学习等领域,聚类算法是很有意义的研究内容[1]。物以类聚,聚类是将数据集中的数据对象按照对象间的相似性划分成若干个类,使同一类的对象间差别小,而不同类的对象间差别大[2]。
Kmeans聚类算法是经典且应用广泛的划分方法之一,具有理论可靠、算法简单、收敛速度快、能有效处理大数据集等优点[3]。但是传统的Kmeans算法过度依赖于初始条件。初始聚类数目K值的确定影响了最终的聚类效果和整个算法的收敛速度。假设聚类数目K值已经确定,选取不同的初始聚类中心又会导致不同的聚类结果,随机选取的初始聚类中心点将会增加最终聚类结果的随机性和不可靠性。由此可见,对于聚类初始条件优化的研究在Kmeans聚类算法改进中有着重要的地位。国内外诸多学者致力于Kmeans算法初始条件的研究,以改善K均值算法的聚类效果[46]。
本文提出一种基于优化初始聚类中心的Kmeans算法,该算法在聚类数目K值的确定上和初始聚类中心的选取上都做了改进,避免了传统Kmeans算法的聚类数目和聚类中心的随机选取。UCI机器学习数据库数据集的实验测试证明,本文所提出的算法具有良好的聚类效果,聚类准确率高。
1 Kmeans聚类算法
传统的Kmeans聚类算法用聚类误差平方和作为衡量聚类效果的准则函数。传统Kmeans算法会随机选择出K个数据作为最初的聚类中心,然后计算出数据集中剩余数据和各聚类中心的距离,根据距离将其余数据分配到各类中,重新确定各个类簇的新中心点,再分配数据集中样本到新的聚类中心,再计算各个类的新中心点,再次分配数据集样本。反复迭代到准则函数收敛为止,也就是聚类中心点不再发生变化。
2 基于优化初始聚类中心的Kmeans聚类算法
2.1 聚类数目K值的确定
聚类算法是通过量化样本间距离和聚类的紧密性来评价聚类效果的好坏。具体表示为:同一个类内数据间的距离越小越好、不同类间的距离越大越好。本文将同一类簇内的差异值和不同类簇间的差异值的比值定义为评价聚类效果优劣的标准。
将数据集所有的类簇内距离和定义为Ein,表示每个类簇中所包含的数据样本到各个类中心点间的距离之和。类簇内距离和Ein的计算公式表示为:
其中,n是表示数据集中所有的样本数量,k表示类的个数,Ci表示第i个类簇,x为第i类中的数据样本,Zi表示第i个类的中心点。类簇内距离和Ein值越小,意味着所有类簇中的数据样本越紧凑,聚类的紧密型越好。
另外,还需要计算各个类簇中心点相互间的距离作为类簇间距离,类簇间距离定义为Eout,类簇间距离Eout的计算公式为:
其中,k表示类的数目,即类簇数,Ci表示第i个类簇的聚类中心点,C表示各个类簇的聚类中心平均值,类簇间距离Eout的值越大,意味着类和类之间的相似度小。
综合类簇内距离和Ein与类簇间距离Eout兩个值来评定聚类效果的优劣性,本文将类簇内距离和Ein与类簇间距离Eout的比值作为聚类效果的评价标准,当类簇内距离和Ein与类簇间距离Eout的比值越小时,表示此时的聚类效果越好。用EE表示聚类效果优劣程度的评价标准,则EE表示为:
由上式可以得出,EE值为先逐渐变小然后会慢慢变大,EE值越小,表示聚类的效果越好,当EE达到局部最小值时,聚类效果最佳,由此可以确定聚类数目K值。
2.2 算法描述
本文通过聚类数目K值的确定和优化初始聚类中心来改进传统Kmeans算法。在确定聚类数目K值时,随着EE=Ein/Eout的值不断变小让K++,当EE值达到局部最小值时来确定K值;优化初始聚类中心时,根据数据集样本分布的特点,选择出K个相距较远的数据样本作为初始聚类中心。本文基于优化初始聚类中心的Kmeans算法一方面解决了传统Kmeans算法中聚类数目K值无法确定的问题,另一方面解决了传统算法中随机选取初始中心点而造成的局部最优问题。
本文基于优化初始聚类中心的Kmeans算法具体描述如下:
(1)初始化:K=1,运行传统的Kmeans算法并计算此时的EE值;
(2)让K++,再次运行传统的Kmeans算法并记录EE;
(3)随着K的逐渐增大运行Kmeans算法,直到EE值出现局部最小值,保留此时的K值,由此确定聚类数目K值;
(4)选择数据集中任意一个数据对象作为第一个聚类中心点;
(5)重复步骤(4),选取出K个初始的聚类中心点;
(6)计算数据集剩余样本到离得最近聚类中心的距离,定义该距离为D(X);
(7)为每个类重新选择聚类中心点,此时选取概率与D(X)的大小成正比,即离原聚类中心越近的点越有可能被选取为新的聚类中心点;
(8)重复步骤(7)直到K个聚类中心点全部被选出来;
(9)再运行传统的Kmeans聚类算法。
3 实验结果与分析
本文实验环境为:Intel CPU,8GB内存,500G硬盘,Windows10操作系统和MATLAB应用软件。
在UCI机器学习数据库[7]的Iris等6个聚类算法常用的测试数据集上对本文基于优化初始聚类中心的改进Kmeans算法和传统Kmeans算法进行实验测试并比较。UCI数据集的描述见表1。
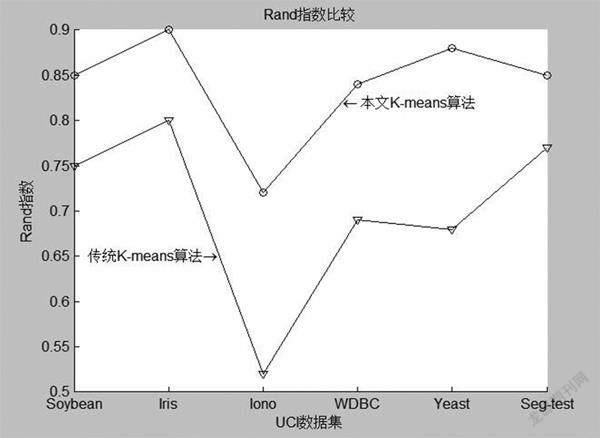
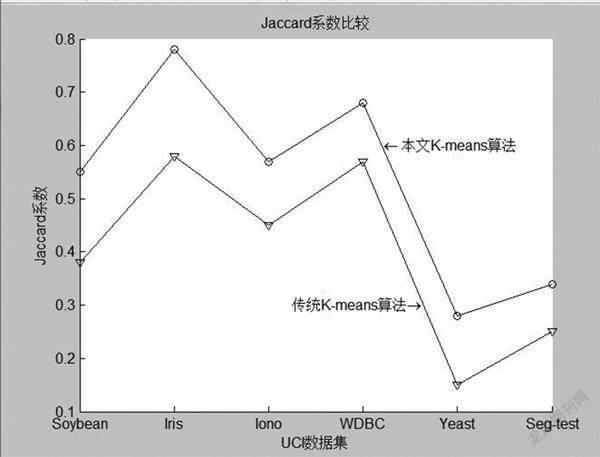
采用聚类误差平方和、聚类时间和聚类准确率、Rand指数、Jaccard系数[89],“Adjusted Rand index”参数[10]对聚类算法的运行结果进行比较分析。表2是本文基于优化初始聚类中心的Kmeans算法和传统Kmeans算法的聚类误差平方和与聚类时间比较的结果。图1~图4分别是两种算法的Rand指数、Jaccard系数、“Adjusted Rand index”参数和聚类正确率的比较结果。
从表2可以看出,在各个数据集上,本文基于优化初始聚类中心的Kmeans算法的聚类误差平方和都小于传统Kmeans算法,有良好的聚类效果。聚类时间的比较显示,本文算法的时间性能略差于传统Kmeans算法,分析原因在于本文算法在确定K值和选取聚类中心点时会消耗一定的时间。
图4显示,在所有数据集上本文基于优化初始聚类中心的Kmeans算法的聚类正确率优于传统Kmeans算法。因此,本文算法获得良好的聚类效果,获得较高的聚类准确率。
结语
本文在分析传统Kmeans聚类算法不足的基础上,提出一种基于优化初始聚类中心的Kmeans算法。该算法通过量化样本间距离和聚类的紧密性来确定聚类数据K值,利用数据集样本的分布特征选取相距较远的初始聚类中心点,克服了传统Kmeans算法对初始聚类中心敏感、聚类效果不理想的缺陷。在UCI机器学习数据库数据集上的实验表明:本文基于优化初始聚类中心的Kmeans算法有很好的聚类效果,准确率高,聚类性能优于传统Kmeans算法。
参考文献:
[1]孙吉贵,刘杰,赵连宇.聚类算法研究[J].软件学报,2008,19(1):4861.
[2]Han J W,Kamber M.Data Mining:Concepts and Techniques,2nd ed.[M].Beijing:Chain machine Press,2000:383466.
[3]谢娟英,郭文娟,谢维信,等.基于样本空间分布密度的初始聚类中心优化K均值算法[J].计算机应用研究,2012,29(3):888892.
[4]韩凌波,王强,蒋正峰,等.一种改进的kmeans初始聚类中心选取算法[J].计算机工程与应用,2010,46(17):150152.
[5]黄敏,何中市,邢欣来,等.一种新的kmeans聚类中心选取算法[J].计算机工程与应用,2011,47(35):132134.
[6]熊忠阳,陈若田,张玉芳.一种有效的Kmeans聚类中心初始化方法[J].计算机应用研究,2011,28(11):41884190.
[7]Frank A,Asuncion A.UCI machine learning repository[EB/OL].Irvine,CA:University of California,School of Information and Computer Science,2010.http://archive.ics.uci.edu/ml.
[8]張惟皎,刘春煌,李芳玉.聚类质量的评价方法[J].计算机工程,2005,31(20):1012.
[9]于剑,程乾生.模糊聚类方法中的最佳聚类数的搜索范围[J].中国科学(E辑),2002,32(2):274280.
[10]杨燕,靳蕃,Kamel M.聚类有效性评价综述[J].计算机应用研究,2008,41(06):16311632.
基金项目:甘肃政法大学校级青年项目(GZF2019 XQNLW08),甘肃省青年科技基金项目(21JR7RA572),2019年甘肃省高校引进和使用优质在线开放课程项目
作者简介:郭文娟(1986— ),女,甘肃武威人,讲师,研究方向:智能信息处理。
