不完备质量下的报童问题及其评估机制

李胃胜, 陈 杰,2, 陈志祥

(1.海南热带海洋学院 理学院,海南 三亚 572022; 2.华南理工大学 工商管理学院,广东 广州 510641; 3.中山大学 管理学院,广东 广州 510275)

0 引言

近年来，随着“缺陷产品召回”和食品安全等事件的发生，产品的质量问题受到社会舆情的普遍关注。例如，2016年上半年，我国对缺陷汽车和消费品实施召回，涉及车辆和消费品数分别达到881.82万辆和478.43万件，较于2015年的同期，分别增长了107%和738%[1]，双汇集团在“瘦肉精”事件曝光后，由于顾客的需求在短期内急剧下降，导致该集团在短短的一个月内经济受损超过121亿元。由此可见，产品的质量问题已成为影响库存系统的供给侧和需求侧的重要因素，其不完备性加剧了对库存系统优化与控制的难度和挑战。实际上，在经济活动中，由于主观或客观等不确定因素的存在，商品的质量水平演变成一个随机动态过程，再加上信息网络技术的快速发展，使得顾客对商品的体验信息在“互联网+”下日趋透明化，以致顾客的需求越来越依赖产品的质量水平。可见，质量水平的不确定性是引起需求随机波动的重要影响因素之一。因此，在不完备质量的环境下，基于需求依赖于质量水平的研究主题，对报童模型进行拓展性研究具有重要的理论和实际意义。

关于不完备质量下的库存系统的决策问题，以下学者做了深入的拓展性研究。Jaggi等[2]考虑将易变质产品的缺陷率依赖时间因素作为决策理念，提出了不完备质量下的两货栈库存模型。Mittal等[3]运用聚类分析、关联性分析和先验算法来收集产品中的缺陷信息，并结合EOQ模型给出了库存的最优订购策略。Alamri等[4]利用学习曲线刻画质量的控制过程，研究100%质量检测下的EOQ模型。Chang等[5]将检测错误信息和交易信用等因素纳入不完备质量下的EOQ模型，其成果表明质量检测错误率和信用影响零售商的最优订购量。Manna等[6]在需求依赖广告效应的条件下，进一步拓展了生产库存模型。Taleizadeh等[7]将混合支付策略纳入报童问题，构建了基于正品和次品混合销售的库存模型。

近年来，关于报童模型拓展性的研究成果主要体现在如下几个方面：

(1)契约协调下的研究成果

Xu等[8]将退货策略、截止时间、道德风险等要素纳入协调机制拓展了报童模型。Wang等[9]在报童模型的理论基础上纳入二次订购和广告策略等因素，提出了新的契约与协调机制。杨亚等[10]综合考虑批发价格契约、新鲜度信息不对称、回购契约等因素对供应链收益水平的影响，并基于Stackelberg博弈拓展了单周期的报童模型。

(2)价格策略下的研究成果

Chua和Liu[11]基于需求的不确定性、销售损失等因素，构建了带有价格策略的报童模型。Wang和Chen[12]同样基于需求的不确定性，在期权契约下构建了带有价格策略的报童模型。Jadidi等[13]在需求为时间和价格依赖的条件下，研究两种价格策略的报童问题。毛照昉和王方圆[14]基于策略消费者的行为属性构建报童模型，并分析消费者行为对定价策略的影响。

(3)风险厌恶下的研究成果

Rubio等[15]运用均值-方差风险厌恶准则研究了带有价格和库存量两个决策变量的单周期的报童问题。Xu等[16]结合CVaR准则研究了带有延期订货的损失风险厌恶报童模型。丁小东等[17]考虑决策者的实际订购行为受风险偏好的影响，并采用CARA效用函数拓展了报童模型，同时从风险偏好的角度解释决策偏差的形成机制。

上述针对报童模型的拓展性研究，主要围绕若干个经典的研究主题，比如：缺货、促销、资源约束等决策理念，进而集成多要素于模型的构建，以解决复杂环境下系统的最优决策问题。然而，尚未有人将需求与质量水平之间的关联性纳入库存系统的基础框架，以拓展报童模型理论及其应用。因此，在不完备质量下，有必要将质量水平对需求的敏感性纳入库存系统的决策机制，以克服传统报童模型在实际应用中的局限性。

1 模型构建

本文在需求依赖于产品质量水平的环境下，考虑报童模型的拓展问题。由于生产、经营活动中有诸多不确定的因素引起产品质量水平的随机波动，故可将质量水平的内在运动规律视为一个随机过程，以刻画库存系统在运作过程中的随机性。这里将产品的质量水平视为库存系统的状态，记状态集W={1,2,…,M}，库存系统的周期k=1,2,…,N；{Yk,k≥0}为产品的质量水平波动过程；记质量水平由i转移到j时的概率为P(Yk=j|Yk=i)=pij，状态转移概率矩阵P=(pij)M×M；第k周期产品质量水平为Yk=i时的需求变量为Xk(i),其概率密度与分布函数分别为fxk(i)(x)及Fxk(i)(x)；第k周期产品的售价、订购成本和残值分别为rk，ck和sk。

1.1 不完备质量的报童模型

令Qk(j|i)为零售商在第k周期产品质量状态由i转移到j时的订购量，那么相应的利润为

Πk(Qk(j|i))=(rk-ck)Qk(j|i)-

(rk-sk)(Qk(j|i)-Xk(j))+

(1)

于是，零售商在第k周期产品质量状态由i转移到j时所获得的期望利润为

E(Πk(Qk(j|i)))

(2)

由此可知，零售商在第k周期质量水平处于初始状态i时所获得的总期望利润模型为

(3)

该模型在经典报童模型的理论框架上引入了需求依质量水平运动的随机过程，进而利用库存系统数据的统计规律性来探究系统总期望利润的变化趋势。

1.2 模型的最优解

需求密度是随机库存系统的理论基础，由于质量水平波动性，其产生的“噪声”影响着库存系统的决策机制。以下主要在不完备质量的环境下，给出模型的最优解。

(4)

命题1的结论体现了产品质量的不完备性、需求的随机性等因素对报童问题的决策机制的影响，解决了零售商在复杂的随机环境下最优订购决策问题。

1.3 不完备质量下库存系统的评估机制

如何构建库存系统随机性的评估体系是运营管理的核心问题。以下利用随机过程的基本理论来刻画库存系统的风险性问题。

1.3.1 首达利润目标的评估机制

由(4)式可知，库存系统的最优订购量受到来自于质量水平随机性的影响，不同的质量状态对应着不同的最优解。假设决策者以状态集A⊂W为考察库存系统的收益目标，于是可得如下重要的结论，这里称之为首达利润目标的评估机制。

(5)

在报童问题中，由于生产与运作管理中存在多重的不确定因素，进一步增加了决策空间的维度和经营的风险性。零售商在第k周期处于某个初始质量状态时所关注的一个问题：如何确定首次达到预期的利润水平的时间和相应的平均利润？命题2的结论很好解决了这方面的问题，即可利用首达利润目标的评估机制，给出零售商获得预期销售利润情况的动态数据信息集:

决策者可利用信息集中的相关元素，以获取支撑决策机制的数据依据。

1.3.2 库存系统的加权平均准则

若零售商R跟供应商S商议签订长期供货的契约，那么在不完备质量的环境下，如何评估零售商R在未来周期内的绩效性？本文利用质量过程中的状态来构建新的评估机制，以分析零售商预期利润依时间维度演变的运动过程。

(6)

由加权平均准则(6)式可知，当γk(A|i)的取值越大时，零售商R在未来每个周期所获取的收益就越大。因此，在此情形下，若供应商S供应商品的质量水平属于指标集A的可能性越高时，零售商R跟供应商S签订长期的供货契约获益的几率就越大，同时在库存系统的未来运作管理过程中所面临的风险性就越小，否则反之。可见，在不完备质量下，利用本加权平均准则，可以从长期行为的视角来评估库存系统可靠性和安全性。

2 数值算例

2.1 不同初始状态下模型的最优解

为了便于模型的计算与分析，这里不妨假设产品质量水平的状态集为W={1,2,3,4,5},即根据产品质量的缺陷率的程度，将其质量水平统一划分为5个状态，状态的取值越小，说明产品的质量水平就越高。为此，假设当产品质量水平处于状态i时，其需求变量的概率密度函数为

(7)

显然，顾客的期望需求关于状态的取值具有单调递减性。

现将上述需求密度与表1中的参数值和转移概率矩阵，分别代入(2)、(3)和(4)式可得，在需求受随机质量波动下的最优期望订购量和期望利润(详见表1所示)。

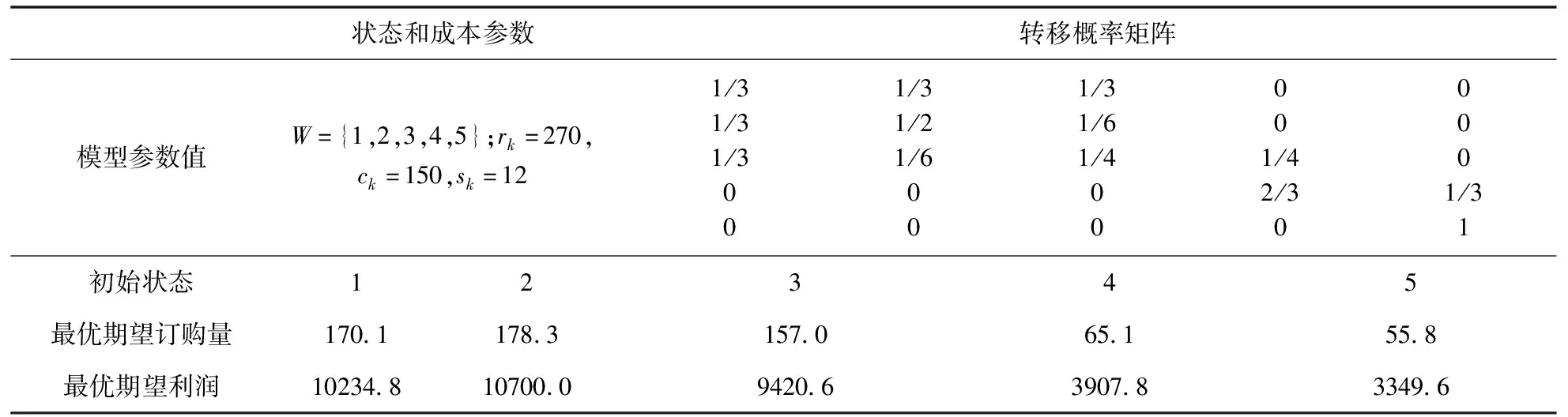
表1 不同初始状态下模型的最优数值解

由表1可知，当质量水平的初始状态处于2时，库存系统的最优期望利润最大，而处于状态5时，相应的最优期望利润最小。按经典库存系统的基本结论，即成本参数保持不变的情况下，顾客的需求越高，库存系统所获取的利润就越大。然而，在本算例中，当质量水平处于最佳初始状态1时，其最优期望利润并不是最大。这是库存系统的决策机制纳入随机因素后，所产生的最有趣的系统“噪声”之一。下面从状态的转移性解释该“噪声”产生的原因。由表1可见，系统稳定在状态“1”的概率为1/3，而转移到其它低质量水平的概率为2/3。系统稳定在状态“2”的概率为1/2，从“2”转移到其它低质量水平的概率为1/6，而转移到高质量水平的状态“1”的概率为1/3。于是，根据需求与质量水平的关联性可知，系统从状态“2”出发，在下个周期的期望需求要比从状态“1”出发的大一些，因此所获取的期望利润也高一些。这表明在需求受产品质量水平的约束条件下，产品质量水平的波动性、需求的随机性以及两者之间的关联性对模型的最优解都具有重要的影响。

2.2 质量水平对最优订购量的敏感性分析

下面从向量代数的视角，讨论质量水平的波动性与最优期望订购量之间的关联性。记初始状态i向各个状态的转移概率向量为Pi=(pi1,pi2,…,piM)，模型(3)的最优解为

于是，相应的最优期望订购量为

(8)

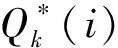
以下只对1)的情形进行数值分析，2)的情形可类似讨论。这里取状态集为W={1,2,3}，转移概率向量αk(k=1,2,…,6)的取值如表2所示。若质量水平的初始状态为i=1，则可得模型(3)的最优解

表2 质量水平对最优期望订购量的影响

2.3 质量波动对最优策略的影响性分析

本小节讨论质量水平不确定性与周期性随机波动对最优策略的影响。在不考虑采购决策受质量水平周期性随机波动影响下，设质量水平Y是一随机变量，其概率密度为fY(y)，市场需求依赖于产品质量水平，记为XY，其概率密度和分布函数分别记为fXY(x)和FXY(x)。类似于式(2)，可得零售商在产品质量水平Y下的期望利润为

(9)

其中Q，r，c和s分别表示产品的订购量、售价、订购成本和残值。于是，零售商的决策行为描述为

(10)

类似于前文推导方法，可知模型存在唯一的最优解Q*，使得

(11)

表3 质量水平周期波动性对最优订购量差的影响

由表3可知，每周期中不同初始质量水平下的最优订购量差具有浮动性，例如，第1周期质量水平处于三种状态下的最优订购量差分别为60.2、-28.3、18.3；而且不同周期间的最优订购量差浮动程度亦具有差异性，如第1周期三种状态处最优订购量差的平均值为(60.2-28.3+18.3)/3=16.7，第2周期三种状态处最优订购量差的平均值为-11.8。此外，从横向时间方面来看，每一初始状态下的最优订购量差随着时间而随机波动，并且具有波动方式多样化和波动程度不均衡的特点。于是，在质量水平随机波动环境下，若决策者采取Q*的订购策略,则在其运营的过程中，可能面临一定的利润损失的风险。这说明在不完备质量的复杂环境下，模型(3)比模型(10)具有较强的适应性。

2.4 可靠性分析及其收益评估

假设某产品的供应商有甲、乙、丙等3家，每家供应商的产品质量水平都具有3个状态，其状态转移矩阵由表3所示。下面将讨论零售商在各供应商所提供的质量水平下，其最优期望订购量和最优期望利润的变化趋势是否具有可靠性以及评估系统的运作的收益性。以下所涉及到的参数和概率密度，如表2所示。

2.4.1 随机库存系统的可靠性分析

(12)

(13)

于是，根据式(12)和(13)可分别计算出各个周期的最优期望订购量与最优期望利润(详见表4中的数据结果)。

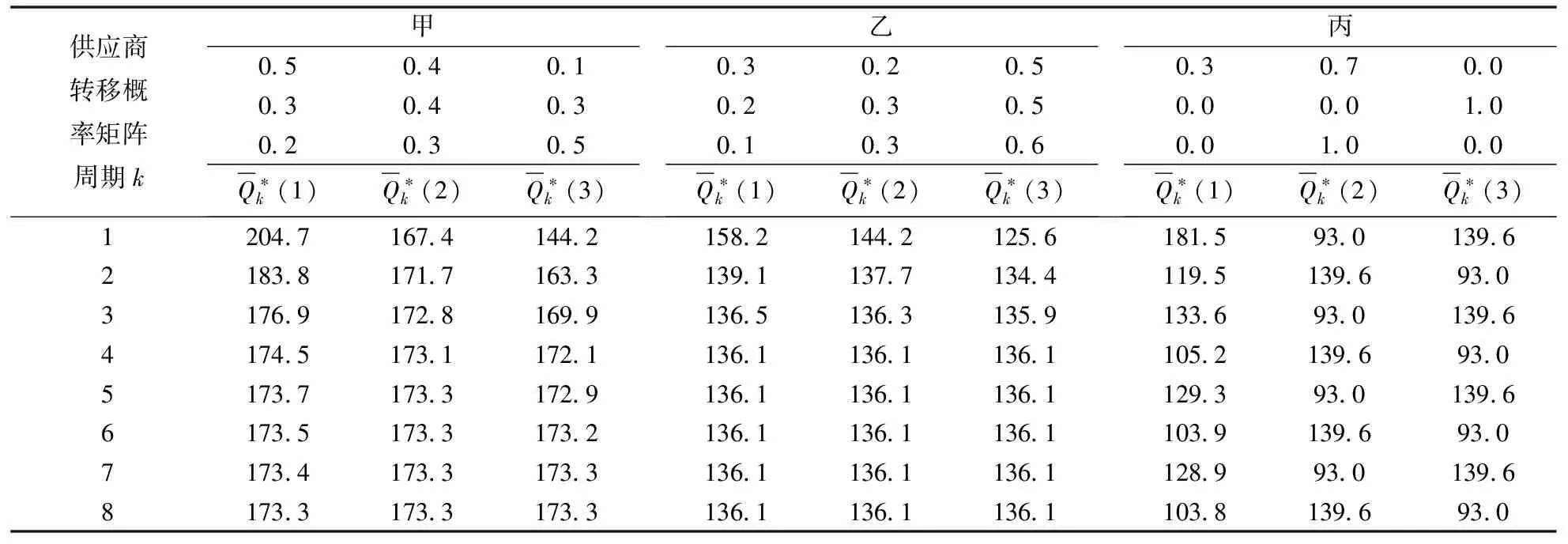
表4 不同供应商的产品质量水平对最优期望订购量的影响

根据表4的数值实验结果可知，在甲供应商的产品质量水平波动环境下，零售商从第8周期起各个初始状态下最优期望订购量的平稳值为173.3，而对乙而言，相应的最优订购量的平稳值为136.1。在丙供应商的产品质量水平波动环境下，零售商从第1周期起各个初始状态下的最优期望订购量不具有平稳性。事实上，由表4易知甲和乙的产品质量水平的各个状态都是互通和遍历的，故两者的质量水平随机波动过程为不可约的马氏遍历链。从而，甲和乙的产品库存系统具有良好的稳定性。再由丙供应商的产品质量水平的转移概率矩阵的属性，可知状态2和3互通，而状态1与2(或3)不互通，故其状态集可分解为两个闭集{1}和{2,3}，可见该供应商的产品质量水平的随机波动过程不满足不可约性。因此，该供应商产品下所对应的库存系统不具有可靠性，从中也表明了若销售商以丙供应商作为货源，其在运作与管理过程中所面临的潜在风险性较大。

2.4.2 随机库存系统的收益评估

在随机库存系统的优化和控制过程中，往往以该系统的若干状态构成一个目标状态集，进而通过系统到达目标状态集的可能性，间接评估系统的未来收益趋势。以下利用数据模拟和仿真的方式，给出不同供应商产品的质量水平随机过程，并以系统的状态1和2作为目标状态集，考察系统到达利润目标的情况，进而评估随机库存系统的运作绩效性。为了消除初始状态对系统的决策机制所产生的差异性，不妨假设各个供应商产品的初始质量状态都为3。各供应商的产品质量水平的转移概率矩阵如表5所示。

表5 不同供应商的产品质量水平的转移概率矩阵

根据表5中的参数与(6)式进行数值计算，并拟合出各供应商下加权平均准则的运动曲线，据此对库存系统的决策机制的长期效应和短期效应进行分析，具体结果如图1所示。

由图1可知，在不完备质量环境下，虽然丙供应商所提供的商品使得零售商的获益水平具有下降的趋势，但是在1至5.5期间内较于其他供应商而言，其预期累积利润的加权平均准则的取值是最大的。然而，随着周期数的增大，在5.5周期之后，乙供应商下的预期累积利润的加权平均准则的取值在其他供应商的取值之上。由此表明，当零售商面临着三个供应商的供货选择时，在短期决策行为下，应该选择丙供应商作为进货渠道，然而在长期决策行为下，应该选择乙供应商作为长期合作的供货方。

3 结论

在实际问题中，库存系统供给侧中的商品质量水平对顾客的需求具有重要的影响。为此，本文从需求依赖于质量水平的视角，利用马氏理论拟合了质量水平与需求之间关联性的动态演变过程，进而将“不完备质量”的决策理念纳入报童模型的理论框架，提出了新的随机库存系统的决策模型及其绩效的评估体系。本研究得出的结论及其管理意义如下：

其二、在不完备质量的环境下，供给侧中质量水平的运动属性确定了随机库存系统的可靠性。当质量水平波动随机过程{Yk,k≥0}为不可约遍历马氏链时，库存系统具有良好的可靠性，否则反之。这意味着当随机过程{Yk,k≥0}不满足不可约性或遍历性时，该系统在运作过程中将面临一定的潜在风险。决策者应根据马氏链{Yk,k≥0}的转移概率矩阵的属性完善系统的决策机制，以达到规避风险的经营目标。

其三、决策者可以通过本文所提出加权平均准则评估随机库存系统在运作与管理过程中的收益问题，从中揭示不完备质量下随机库存系统的运动趋势，以解决供应商的最佳选择问题。因此，决策者可根据加权平均准则来获取的预期收益信息进而设计相应的供货契约机制，使得本方获益最大化。