台风灾害预警—应急响应两阶段决策方法
2022-02-16周朋杨付江月
陈 刚, 周朋杨, 付江月
(贵州大学 管理学院,贵州 贵阳 550025)
0 引言
台风灾害发生频率高、破坏强度大、影响范围广,是最严重的自然灾害之一。台风领域的科学家长期致力于提高台风的预报精度,近年来取得显著成效,但预报的精准性与预报时效通常成反比[1]。因此,气象部门通常会提前24~36小时发布台风的预报信息,以及提前3~4天对台风未来的强度、动向和可能影响的地区发布信息。应急管理部门可根据以上信息预测可能出现的灾害情景以及其发生概率,提前制定防灾减灾措施,以较低的成本和较小的伤亡损失完成应急响应任务。这时就可以采用两阶段决策,即在能够预测灾害情景及其发生概率时的预警阶段就采取一定的防灾减灾措施,缓解应急响应阶段人员紧急转移安置时由于资源短缺和时间紧迫带来的风险,且预警阶段由于资源和时间充裕,单位转移安置成本往往比应急响应阶段成本低。此外,由于灾害的复杂性和不确定性,方案的决策信息往往不能给出精确值。因此,如何根据这些不确定情景的预测信息及不确定的决策信息,对台风灾害进行有效的应对,以降低其对经济和社会的影响,是一个具有一定理论价值和现实意义的课题。
目前针对不确定环境下的应急决策方法已有一些研究成果。例如,Ding等[2]利用毕达哥拉斯模糊语言变量表示不确定性,提出一种基于前景理论的动态应急决策方法;Zhan等[3]用毕达哥拉斯模糊粗糙集表示不确定性,提出一种基于PF-TOPSIS的非常规突发事件决策方法;徐选华等[4]利用非均衡语言D数表示不确定性,提出一种大数据环境下的大群体风险性应急决策方法;杨乃定和吴静杰[5]采用直觉模糊软集描述不确定性,提出一种基于TOPSIS的煤矿应急救援决策方法;陈雪龙和王亚丽[6]采用语言术语集描述不确定性,提出一种基于证据理论的多属性应急决策方法;张磊等[7]运用贝叶斯网络扩展知识元模型的不确定性,提出一种面向突发事件应急决策的情景建模方法;Liu等[8]以不同情景的发生概率描述不确定性,提出一种基于累积前景理论的应急风险决策方法。
后悔规避是应急决策者常见的一种心理行为,后悔理论自1982年提出以来受到学者的广泛关注,近年来也开始应用于应急决策。例如,徐选华等[9]利用后悔理论计算各个方案在不同状态下的感知效用值,提出一种面向冲突风险熵和后悔规避的大群体应急决策方法;袁媛等[10]针对突发事件存在多种可能情景的应急决策问题,提出一种考虑后悔规避的应急响应风险决策方法;钱丽丽和刘思峰[11]针对实施不同方案各情景发生概率不同的应急决策问题,提出基于后悔理论和区间灰数信息的应急决策方法;姜艳萍等[12]同时考虑决策者的后悔心理行为和失望心理行为,提出一种针对具有混合多指标信息的应急方案选择方法。
已有的研究大多是针对灾害或突发事件发生前的防灾减灾措施决策或发生后的应急响应措施决策,然而,针对一些可预测的自然灾害,可提前采取一些预警措施,以减轻应急响应阶段的压力,又由于受资源及时间等方面的限制,应急响应措施的实施效果往往与灾害发生前的预警措施相关,因此需要同时考虑事前预警措施及事中应急响应措施两阶段的应急决策问题。目前,虽然已有一些关于两阶段应急决策方法的研究[13,14],但都只是将决策流程分为两个阶段,本质上还是针对一次性决策方案的选择问题。针对事前—事中两个阶段的应急决策,只有刘洋等[15]在考虑决策者过度应对后悔和应对不足后悔行为基础上,提出一种事前防灾减灾措施选择及事中应对措施选择的两阶段应急决策方法。因此,本文基于后悔理论的思想,进一步考虑决策信息和情景概率的不确定性,提出一种考虑不确定情景预测信息的台风灾害预警—应急响应两阶段决策方法。
1 问题描述
台风灾害的应对一般分为预警与应急响应两个阶段,预警阶段一般为台风过境前的3~4天,该阶段的决策时刻记为t1,应急响应阶段一般为台风过境前的24~36小时,该阶段的决策时刻记为t2。虽然各阶段的决策时刻不同,但各阶段不是孤立的,需要全局考虑。为方便起见,记M={1,2,…,m},N={1,2,…,n},H={1,2,…,h}。
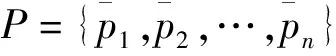


2 原理与方法
2.1 应急响应阶段的决策
2.1.1 决策矩阵规范化
(1)
(2)
2.1.2 成本向量规范化
(3)
2.1.3 综合效用计算

i∈M,j∈N,l∈H,k=1,2,…,mi
(4)
i∈M,j∈N,l∈H,k=1,2,…,mi
(5)
(6)
(7)
2.2 预警阶段的决策
2.2.1 后悔—欣喜值计算
构造后悔—欣喜函数R(Δv),函数R(Δv)是单调递增的凹函数,满足R′(Δv)>0、R″(Δv)<0且R(0)=0,表示应急管理部门对于后悔和欣喜都是风险规避的,且对于两个结果没有差异的方案即不感到后悔也不感到欣喜。根据后悔理论,R(Δv)可以表示为R(Δv)=1-exp(-δΔv),其中,δ为应急决策部门的后悔规避系数,δ>0,且δ越大,表示后悔规避程度越大。Δv表示关于两个方案结果效用值之差的变量,R(Δv)表示后悔—欣喜值,当Δv>0时,R(Δv)>0,R(Δv)表示欣喜值;当Δv<0时,R(Δv)<0,R(Δv)表示后悔值。且Δv>0当时,有|R(-Δv)|>R(Δv)成立,表示应急管理部门对后悔的心理感知比对欣喜的心理感知更加敏感,是后悔规避的。
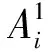
(8)
2.2.2 区间概率转化
(9)
最大熵法可以在仅使用现有信息的条件下推断出最有可能出现的概率分布,在决策分析中广泛应用。因此,本文采用最大熵法进行区间概率转化,通过求解如下最优化模型获得点概率向量。
2.2.3 综合后悔—欣喜值计算
(11)
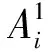
2.3 决策方法步骤
综上,考虑决策者风险规避和后悔规避心理行为的台风灾害预警—应急响应两阶段决策方法的步骤如下:

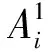
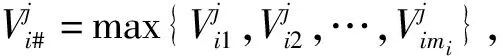
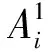


3 算例研究
3.1 算例描述
以2019年浙江省W市应对台风“利奇马”过境时,人员转移安置方案选择问题为背景给出算例。2019年8月7日9时(t1时刻),W市应急管理部门综合各类数据,预计台风过境时,最大风速可出现“6~7级(S1)”、“8~9级(S2)”、“10~11级(S3)”、“12级及以上(S4)”等4种情景,各情景的概率分别为P={[0.4,0.6],[0.2,0.4],[0.1,0.2],[0.05,0.1]},此时实施预警措施。预计台风8月10日凌晨过境,8月9日6时(时刻)预测精度将进一步提高,可确定台风的具体情景,并采取相应的应急响应措施。预警—应急响应措施方案及成本如表1所示。在进行方案选择时,主要考虑以下3个指标:I1为死亡失踪人口,I2为直接经济损失,I3为社会影响,其中I1和I2为成本型指标,I3为效益型指标。所有指标都可通过专家判断给出,但由于灾害的不确定性,I1和I2用区间数表示,又由于社会影响不好量化,故I3可用语言变量表示。依据专家判断,确定了决策矩阵,如表2所示,其中语言变量与区间数之间的对应关系如表3所示。由于应急管理的弱经济性及人道主义精神,假设决策者给出的权重向量W=(wC,w1,w2,w3)=(0,1,0.5,0.1,0.3)。根据文献[12,15],取风险规避系数α=0.8,后悔规避系数δ=0.3。
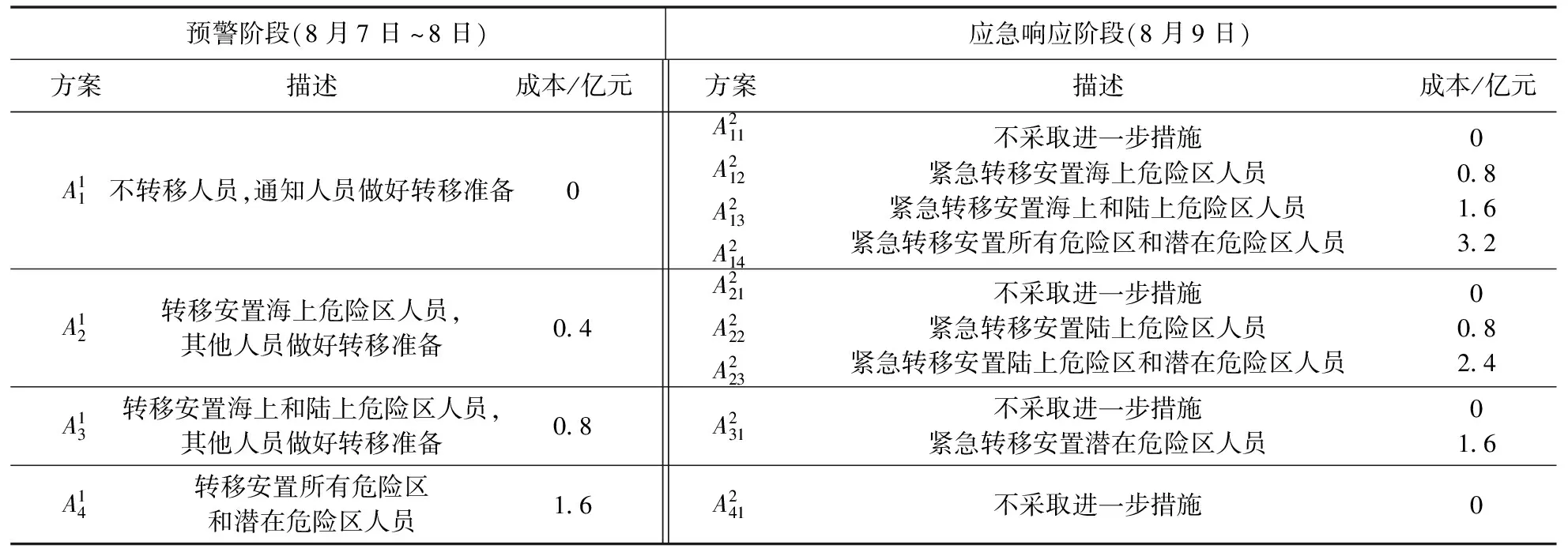
表1 台风灾害预警—应急响应措施方案及成本

表2 算例的决策矩阵
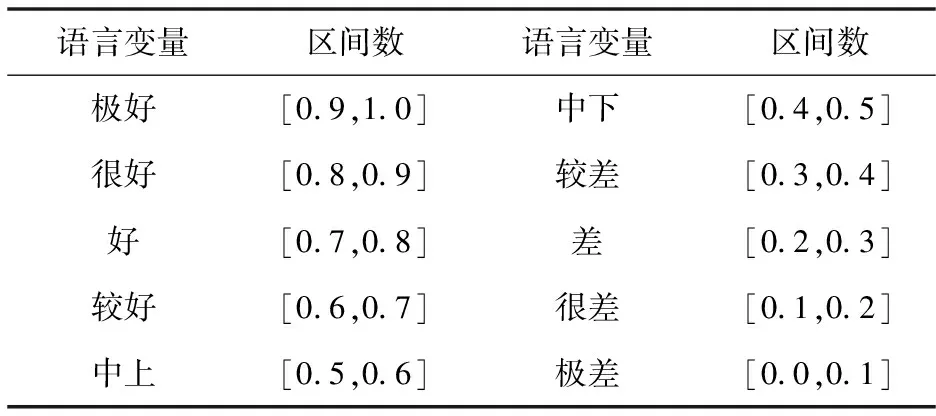
表3 语言变量与区间数之间的对应关系
3.2 结果分析
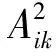

表4 t2时刻实施应急响应措施来应对情景Sj的综合效用
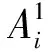

表5 t2时刻出现情景Sj时预警措施相对于预警措施的后悔—欣喜值
3.3 对比分析
3.3.1 不同决策者偏好的对比


表6 不同权重下的方案排序与最优措施
3.3.2 不同决策方法的对比
4 结论
本文针对台风灾害的应急响应决策问题,提出一种不确定环境下预警—应急响应两阶段应急决策方法。该方法运用不确定情景及区间数描述不确定信息,并采用逆序法进行分析。首先考虑决策者的风险规避行为,通过计算应急响应阶段各措施的实施效用来确定针对不同预警措施和灾害情景下的最优应急响应措施;然后考虑决策者的后悔规避行为,计算任意两个预警措施相比较的后悔—欣喜值;最后通过最大熵法,将不确定情景的区间概率转化为点概率,进而计算出各预警措施的综合后悔—欣喜值及排序值;在此基础上确定最优的预警措施和针对各灾害情景的应急响应措施。
值得一提的是,本文所提出的方法不仅适用于台风灾害,也适用于其他可预测自然灾害(如洪涝、风雹、泥石流等)的应急响应决策,两阶段决策法的核心思想是提前做好预警措施,并针对可能出现的灾害情景制定相应的应急响应措施,最大程度降低灾害造成的人员伤亡及财产损失。此外,本文考虑了决策者的风险规避和后悔规避行为,符合决策者针对现实应急决策问题的心理感知,可为应急管理部门的决策提供辅助支持。
