基于核主成分空间支持向量机的过程监视方法
2022-02-16郭金玉
郭金玉,李 涛,李 元
(沈阳化工大学 信息工程学院,辽宁 沈阳 110142)
随着现代工业生产过程日益复杂,有效提高控制系统的故障检测性能变得尤为重要。在工业生产过程中,基于数据驱动的控制系统故障检测方法快速发展。近年来,以主成分分析 (principal component analysis, PCA) 为代表的多元统计方法发展迅速,并衍生出了众多故障检测方法[1-5]。PCA是一种线性降维方法,在数据满足单一分布的基本假设下,解决相关过程变量引起的线性问题,对数据的信息提取和压缩也取得很好的效果。但实际工业生产过程中存在众多非线性、多模态和非高斯特征的数据,不满足单一分布的假设,PCA方法难以得到令人满意的检测效果[6]。核主成分分析(kernel principal component analysis,KPCA)[7-9]将低维空间中的非线性数据映射到高维特征空间,在高维特征空间中建立PCA模型进行故障检测,在一定程度上扩大了PCA方法的使用范围,提高了对非线性数据的处理能力。为了解决工业生产过程中的数据非线性和动态性等问题,王亚君等[10]提出一种多动态核主成分分析的故障检测方法,构造了适合批量生产过程的多模态、非线性和动态模型建立方法。针对复杂工业系统中的动态非线性故障检测方法精度低和计算量大的问题,翟坤等[11]提出一种改进的动态核主成分分析的故障检测方法,提高了KPCA的故障检测性能,同时对微小故障的检测也更为敏感。
支持向量机(support vector machine, SVM)被提出后,因强大的泛化能力和在解决分类问题方面的优势,受到国内外学者[12-14]的广泛关注,成为机器学习中的经典方法。SVM的分类思想是找到最大分离超平面,进而将样本有效分类。针对非线性过程中SVM的检测性能不足问题,Zhang等[15]结合核独立成分分析(kernel independent component analysis, KICA)、KPCA和SVM的优点,开发了一种非线性动态检测方法。Yu[16]提出基于支持向量聚类的概率方法,通过支持向量建立超球面,将故障数据和正常数据分开,实现故障检测。为了进一步提高SVM的故障检测性能,Hsu等[17]将独立成分分析(independent component analysis, ICA)和SVM方法相结合,提高了SVM在多变量过程中的监测能力。王东等[18]提出基于核主成分分析和最小二乘支持向量机(kernel principal component analysis and least squares support vector machine, KPCA-LSSVM)的故障识别方法,比传统的分类方法故障识别速度快、分类准确率高。后续的研究与应用多集中在提高SVM的故障检测性能和丰富其应用场景上。
为了提高SVM在工业过程中的故障检测性能,提出一种基于核主成分空间支持向量机的过程监视方法。运用KPCA对数据进行处理,计算Hotelling′sT2统计量;在T2统计量基础上加入时滞特性和时差特性,将三者组合成增广矩阵,作为输入训练SVM模型;运用训练的SVM模型对测试数据进行故障检测。本研究通过增加模型输入的复杂度在一定程度上去除样本间的自相关性,提高SVM的故障检测性能。
1 基于核主成分空间支持向量机的过程监视
1.1 支持向量机
SVM在处理工业数据时,往往会面临着众多的非线性数据,由于非线性数据无法处理,需要将其投影到高维空间,去除数据非线性,建造最大分离超平面,使数据能够被有效分类。由于分离平面是基于支持向量构造的,所以SVM是解决高维问题的一种很好方案。核函数的引入,也避免了高维计算的复杂度。
假设给定的样本训练集为H={(x1,y1),(x2,y2),…,(xm,ym)},yi∈{-1,+1},其中有两类样本,需要找到最大分离超平面将两类样本进行有效分类,这是分类学习最基本的思想。要建立超平面,就要获得权重向量w和位移项b,两者决定了超平面的划分,影响样本的分类准确率。找到有最大间隔的超平面,也就是要找到满足条件的参数w和b,使得分类间隔γ最大,使两类样本最大程度分开,得到更好的分类效果。因此,SVM基本模型可表示为:
(1)
s.t.yi(wTxi+b)≥1-ξi,i=1,2,…,m。
其中:C>0是惩罚参数,其引入能够在一定程度上解决SVM对一些样本分类出错的问题;ξi是松弛变量,用于表征样本不满足最大分离超平面的约束程度。
为了求解式(1),需要将其转化成“对偶问题”,使用拉格朗日乘子法求解。该问题的拉格朗日函数表示为:
(2)
其中,αi≥0,μi≥0是拉格朗日乘子。在求解过程中,数据往往具有较强的非线性,为了更好地解决这一问题,需要通过非线性映射φ投影到高维空间。为了避免高维运算,引入核函数:
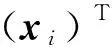
(3)
通过核函数能够避免在高维特征空间中内积的计算,对偶问题可表示为:
(4)
求解后的支持向量展式为:
(5)
因此,SVM在对数据进行分类时,对训练数据进行模型训练,求解式(5)的判别函数。当测试数据输入模型时,判别函数能够对其进行有效分类。无论数据是线性还是非线性,SVM都可以进行有效转化,通过模型训练学习数据变化特征,进而高效准确地对数据进行分类。
1.2 基于核主成分空间的支持向量机方法
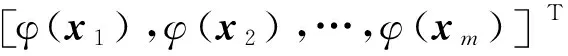
(6)
对协方差矩阵S进行特征向量分析,即
(7)
式中,λi为协方差矩阵的特征值,Pi是特征值对应的特征向量,即
(8)
其中a=(a1,a2,…,am),ai为核函数矩阵的第i个特征向量。根据累计方差贡献率(cumulative percent variance,CPV)[19]求取核主成分个数z,如下式:
(9)
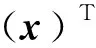
(10)
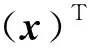
Ka=mλia。
(11)
φ(x)在特征向量Pi上的投影为:
(12)
故在核主成分空间中T2统计量定义为:
T2=yTΛ-1y。
(13)
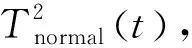
(14)
在故障操作条件下获取故障数据,同样在核主成分空间中建立故障数据的增广矩阵:
(15)
将正常数据与故障数据的增广矩阵作为SVM模型的训练数据,定义为:
(16)
将包含正常和故障数据的增广矩阵输入SVM模型,进行模型训练,获得判别函数。训练后的SVM能学习到正常和故障数据的特性,对数据进行正确分类。将测试数据输入模型,通过超平面划分,正常数据划分成一类,将其定义为标签0;故障数据划分成另一类,将其定义为标签1。
1.3 基于核主成分空间支持向量机的过程监视
基于核主成分空间支持向量机的过程监视主要包括离线模型建立和在线故障检测两个部分。
离线模型建立步骤为:
1) 收集正常操作条件下的历史数据集X1和故障操作条件下的历史数据集X2;
2) 运用核主成分分析方法在核主成分空间分别建立正常和故障数据的T2统计量;
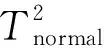
5) 对SVM模型进行训练,获得判别函数。
在线故障检测步骤为:
1) 对于测试数据集xnew,利用离线建模数据的均值和方差对其进行标准化处理;
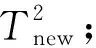
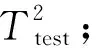
4) 通过SVM模型对测试数据进行分类,实现对故障的检测。分类标签为0的数据为正常样本,而标签为1的数据为故障样本。
2 仿真结果与分析
2.1 非线性数值例子
构造由两个变量组成的非线性数值例子,生成模型如下:
(17)
式中,e1和e2分别是服从均值为0、标准差为0.01的正态分布的白噪声,t服从[-2,2]的均匀分布。
由该模型产生200组正常数据,并分别对变量1和变量2施加0.01×(i-100)和0.5的阶跃故障,产生300组故障数据。由于SVM模型训练需要加入正常和故障数据,因此,本例中由200组正常数据和200组故障数据共同组成训练数据集,其余100组故障数据用于模型测试。PCA、KPCA和KPCA-LSSVM方法的主成分个数由85%累计方差贡献率确定,SVM方法中的惩罚参数C和核窗宽参数g通过寻优测试分别设置为0.8和0.25。图1是样本散点图。图2是5种方法的故障检测对比图,从图中可以看出PCA和KPCA两种方法的故障检测效果并不理想,在控制限上方的故障样本数较少,说明这两种方法对故障样本的检测效果较差。传统的SVM方法在训练时加入了故障数据,模型训练时能够有效学习到故障的变化特征,因此检测效果优于PCA和KPCA。但是样本间的时刻相关性会影响传统SVM的检测效果,因此传统SVM方法不能得到满意的分类效果。传统SVM方法把标签为1的故障样本识别为标签0的正常样本数量多于本方法,即漏报样本较多,因此传统SVM方法对故障样本的识别能力不如本方法。在漏报的故障样本数量方面,KPCA-LSSVM好于传统SVM方法,但比本研究方法差。本研究方法通过引入时滞和时差输入特性,在一定程度上增加矩阵的复杂度,去除样本间的自相关性,使数据特征更加显著,能够识别出更多的故障样本,检测效果优于传统的SVM和KPCA-LSSVM方法。

图1 样本散点图Fig. 1 Scatter plot of samples

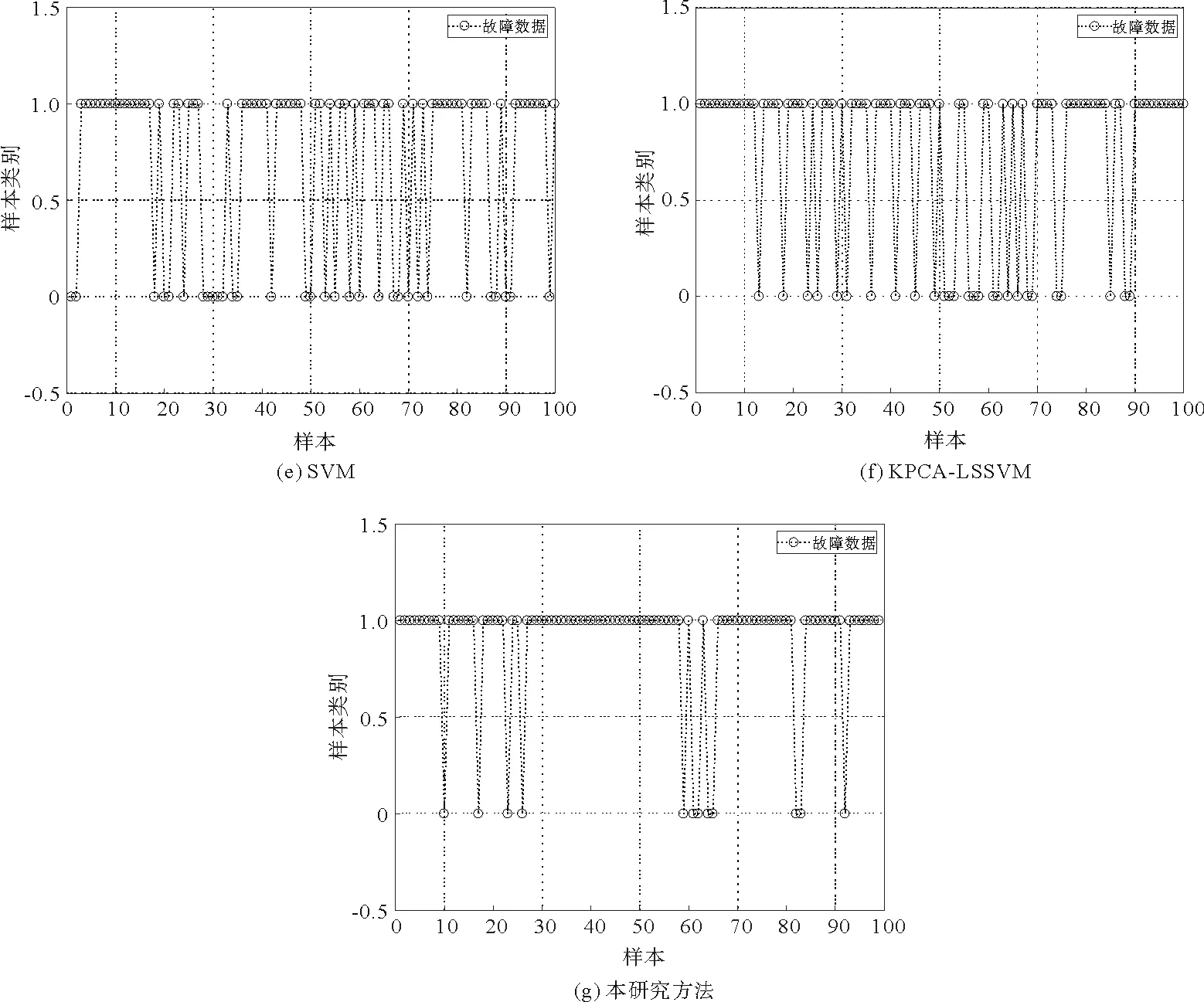
图2 5种方法的检测结果Fig. 2 Detection results of five methods
表1是5种方法故障检测率的对比。从表1中可知,PCA的T2、SPE的检测率分别为9%和13%,KPCA的T2和SPE的检测率分别为14%和12%,传统SVM的检测率为68%,KPCA-LSSVM的检测率为73%,而本研究方法的故障检测率为87.88%。原因在于:PCA缺乏对非线性数据的处理能力,难以得到满意的检测效果;KPCA寻找方差差异最大化的方向投影,其残差空间和主成分空间在一定程度上会丢失部分数据特征,故不能获得较好的检测效果;而SVM具有一定的学习能力,对故障样本的分类准确性高于PCA和KPCA;KPCA-LSSVM结合两者的优点,检测效果略高于传统SVM方法;本研究方法通过引入时滞和时差输入特性,在核主成分空间上建立增广矩阵,增强输入矩阵的复杂度,去除样本间的自相关性,故障检测效果优于传统SVM和KPCA-LSSVM方法。综上,相较于其他4种方法,本研究方法的故障检测率最高。

表1 5种方法的故障检测率对比Tab. 1 Comparison of fault detection rates of five methods
2.2 田纳西-伊斯曼(Tennessee Esatman,TE)过程仿真
TE过程仿真平台已成为国际上通用的工业过程模型仿真平台[21-23],在故障检测和诊断领域得到广泛使用。TE过程变量众多,其中2个气液放热反应会产生2种主产品,与5个主要操作单元等共同组成TE过程。利用TE过程模拟21种预编程故障,丰富多样的故障类型可真实反映实际工业过程中的众多问题。
在TE过程仿真中,以故障类型3、8、9、10、12、13、15、16和19为例,分别从每个故障类型中选取500组故障数据和500组正常数据共同组成训练数据集用于SVM模型的训练,另外选取160组故障数据作为测试数据。在本例中,PCA、KPCA、SVM、KPCA-LSSVM和本研究方法的参数设置与非线性数值例子保持一致。图3是4种方法对故障9的检测结果,其中传统SVM、KPCA-LSSVM和本研究方法都将正常样本的标签定义为0,故障样本的标签定义为1。
由图3可知,KPCA-LSSVM的检测效果优于PCA、KPCA和传统SVM方法,能够检测出更多的故障样本,这得益于KPCA方法对非线性特征的提取,但样本间时刻相关性仍影响故障检测的效果,而本研究方法能够有效地克服这一缺点,检测效果优于其他几种方法。
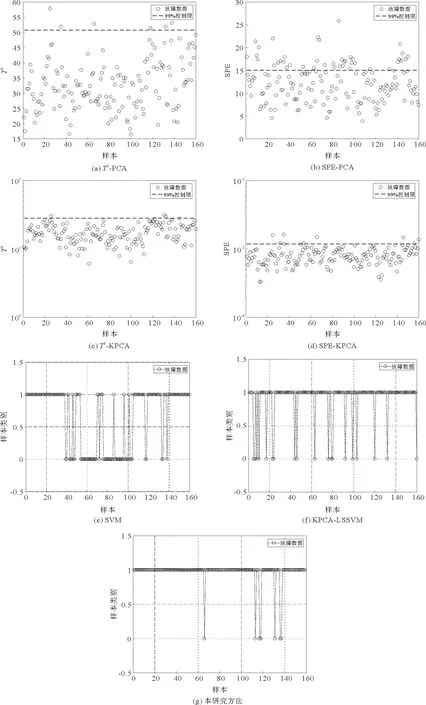
图3 5种方法对故障9的检测效果Fig. 3 Detection results of five methods for Fault 9
表2是5种方法对9种不同类型故障的检测率对比。由表2可知,对于9种不同类型的故障,本研究方法的故障检测率比PCA、KPCA、传统SVM和KPCA-LSSVM方法均有不同程度的提高,验证了该方法的有效性。
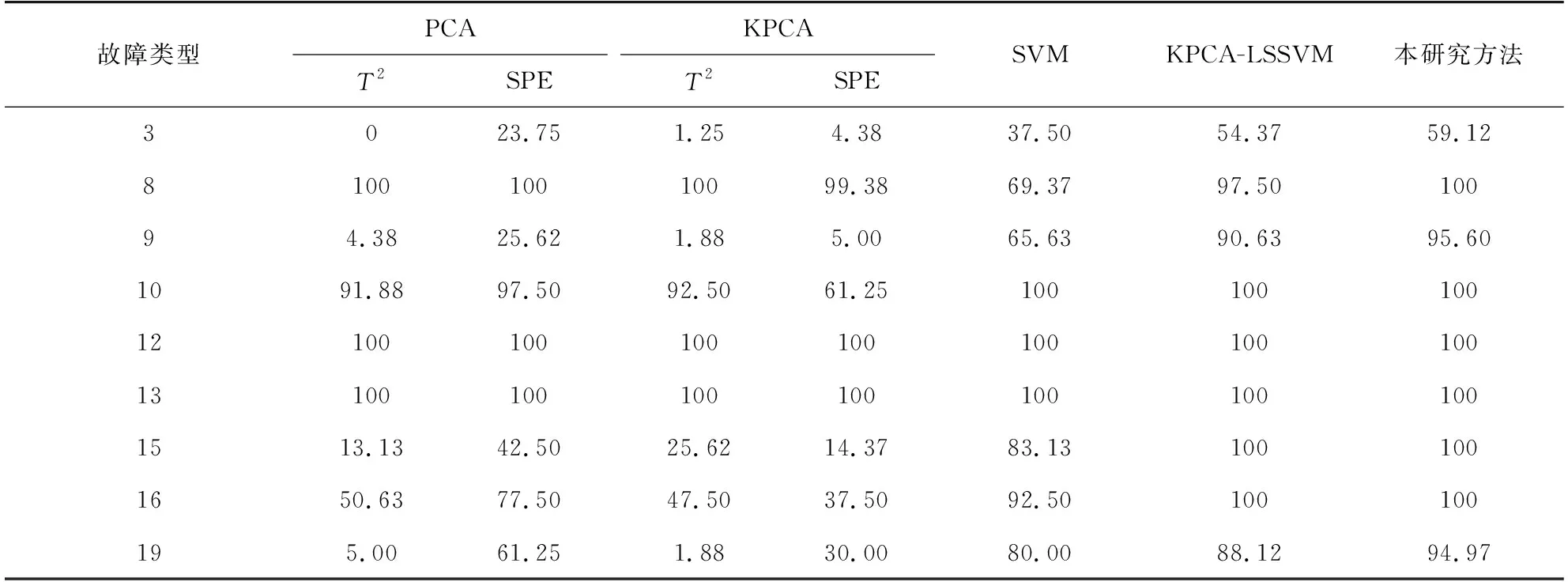
表2 5种方法的故障检测率对比Tab. 2 Comparison of fault detection rates of five methods
3 结论
本研究提出一种基于核主成分空间支持向量机的过程监视方法。运用KPCA方法在低维核主成分空间建立T2统计量,并引入时滞输入特性和时差输入特性作为SVM模型的输入,通过增强模型输入矩阵的复杂度能够有效地降低样本间的自相关性,提高了SVM的故障检测性能。将本研究方法应用于非线性数值实例和TE过程仿真,仿真结果表明,与PCA、KPCA、传统SVM以及KPCA-LSSVM方法相比,该方法能够有效地提高故障检测率。
