镐型截齿不同截割速度对煤岩截割过程影响研究
2022-02-16刘晋霞咸方新
刘晋霞,咸方新,张 超
(1.山东科技大学 交通学院,山东 青岛 266590; 2.山东科技大学 机械电子工程学院,山东 青岛 266590)
镐型截齿具有齿身线条流畅、耐磨损等优点,被广泛应用于采煤机中。镐型截齿煤岩截割过程中,其截割速度直接影响镐型截齿寿命、滚筒装煤效率以及采煤机工作效率等,因此研究镐型截齿不同截割速度对煤岩截割过程的影响具有重要的实际意义。
目前,由于受到实际工作条件的限制,关于镐型截齿截割速度对煤岩截割过程影响的研究,大多学者基于截割试验台试验及数值模拟的方法进行分析。Muro等[1]以及李国华等[2]利用自制截割试验台模拟了镐型截齿不同等速截割煤岩的过程,分别得到不同截割速度对镐型截齿寿命、截割效率以及比能耗的影响规律。应用的数值模拟方法主要有有限元法与离散元法两种;姬国强等[3]与杜鑫等[4]基于有限元数值模拟法,在ANSYS中模拟镐型截齿不同等速截割煤岩时截齿的受力情况;贾嘉等[5]与史小军[6]基于离散元数值模拟法,用PFC3D模拟镐型截齿不同等速截割煤岩过程,分别得到截割比能耗及截割阻力随截齿截割速度的变化规律。
以上镐型截齿截割速度对截割过程影响的研究,均基于等速截割状态进行。然而,在采煤机实际工作中,镐型截齿截割速度不仅随采煤机牵引速度、滚筒角速度变化[7],且在截割过程中也一直处于变化的状态。由于离散元法在模拟煤岩破碎状态、裂纹的萌生、扩展等方面具有明显优势[8],因此本研究基于离散元法,考虑采煤机牵引速度和滚筒角速度对截割速度的影响,建立不同截割速度的镐型截齿煤岩截割模型,分析不同截割速度下截齿截割力以及煤岩内部裂纹扩展的变化规律,从而得到截割速度对镐型截齿截割煤岩过程的影响。
1 镐型截齿截割煤岩过程的截割速度
1.1 截割速度计算
采煤机采煤时,镐型截齿截割煤岩的过程如图1所示。镐型截齿以γ角安装于滚筒上,形成的截割半径为R。当采煤机牵引速度为vq、滚筒角速度为ω时,形成镐型截齿沿截割轨迹切线方向的截割速度va,可由式(1)计算得到[9]。坐标系xOy固定于滚筒轴心,x轴指向采煤机牵引运动方向;O、O1点分别为镐型截齿开始截割煤岩的瞬间以及旋转截割一周期后滚筒轴心的位置。1、2为镐型截齿截割一个周期前、后的截割轨迹,由式(2)、式(3)计算[10]。

图1 镐型截齿煤岩截割过程Fig. 1 Cutting process of conical pick
(1)
(2)
(3)
式中:t为截割时间;T为截割周期,T=2π/ω;H为进给量,H=2πvq/ω;m为滚筒上同一截线的截齿数,本研究基于单齿截割过程进行,因此假设m=1。
1.2 截割过程中截割速度的变化
由式(3)可知,截割速度va不仅与采煤机牵引速度vq与滚筒角速度ω、截割半径R有关,而且还随截割过程t变化。在实际工作过程中,为满足采煤效率以及装煤能力,采煤机牵引速度vq及镐型截齿截割速度va一般分别控制在1~6 m/min和2~4 m/s[11-12]。设镐型截齿的安装角为45°,取截割半径R为0.5 m,将牵引速度、滚筒角速度所表征的截割速度在以上范围内按等差方式取值,以得到不同截割参数下截割过程中其截割速度变化规律。按表1所示采煤机牵引速度vq与滚筒角速度ω分别计算牵引速度与滚筒角速度对镐型截齿截割过程中截割速度的影响情况,如图2所示。下文所述速度序号均与表1对应。

表1 镐型截齿截割速度选取Tab. 1 Selection of cutting speed of conical pick

图2 截割过程中截割速度随牵引速度、滚筒角速度的变化Fig. 2 Changes of cutting speed with traction speed and drum angular velocity in the cutting process
由图2可知,镐型截齿在截割过程中,截割速度总体呈非线性减小趋势,且在T/4时刻减小速率最快;由表1中序号1、2、3不同参数下的变化曲线可知随牵引速度的增加,其非线性增强。当牵引速度为6 m/min时,截割速度在截割过程中的变化可达0.2 m/s以上;由表1中序号4、1、5的变化曲线可知随滚筒速度增加,截割速度明显增大。
2 镐型截齿煤岩截割模型
2.1 镐型截齿模型的选取及建立
选择U94型镐型截齿作为煤岩模型截割工具,其外形如图3(a)所示,使用CAD软件画其外轮廓如图3(b)所示。

图3 U94镐型截齿及外轮廓尺寸Fig. 3 Conical pick U94 and its external dimension
2.2 煤岩样品的三轴压缩模拟试验
根据高为100 mm、直径为50 mm的煤岩样品,在10和20 MPa围压下的三轴压缩试验应力-应变曲线[13],利用PFC内嵌的FISH语言编写颗粒流程序模拟该压缩试验过程,设置煤岩颗粒力学性质参数见表2[14]。

表2 煤岩颗粒力学参数Tab. 2 Mechanical parameters of coal rock particles
为更加接近煤岩的力学性质,选择平行黏结模型模拟煤岩模型中颗粒间的接触方式。在煤岩模型中,选取的颗粒半径越小,越能真实反映煤岩样品的宏观力学性质;但半径过小,会造成颗粒数量过多,影响仿真效率。根据模型最小几何尺寸方向的颗粒数不应小于20的要求[15],颗粒半径范围确定为1.6~2.6 mm。
对试验过程煤岩模型的各黏结参数进行反复调整,最终使模拟压缩试验与文献[13]试验的应力-应变曲线重合度达到95%以上。以围压为10 MPa为例的三轴压缩模拟试验,模型内部各阶段裂纹形成如图4所示。模拟试验应力-应变曲线与试验曲线对比如图5所示,此时煤岩模型的黏结参数见表3。

图4 三轴压缩模拟试验过程各阶段裂纹形成Fig. 4 The formation of cracks during the triaxial compression simulation test
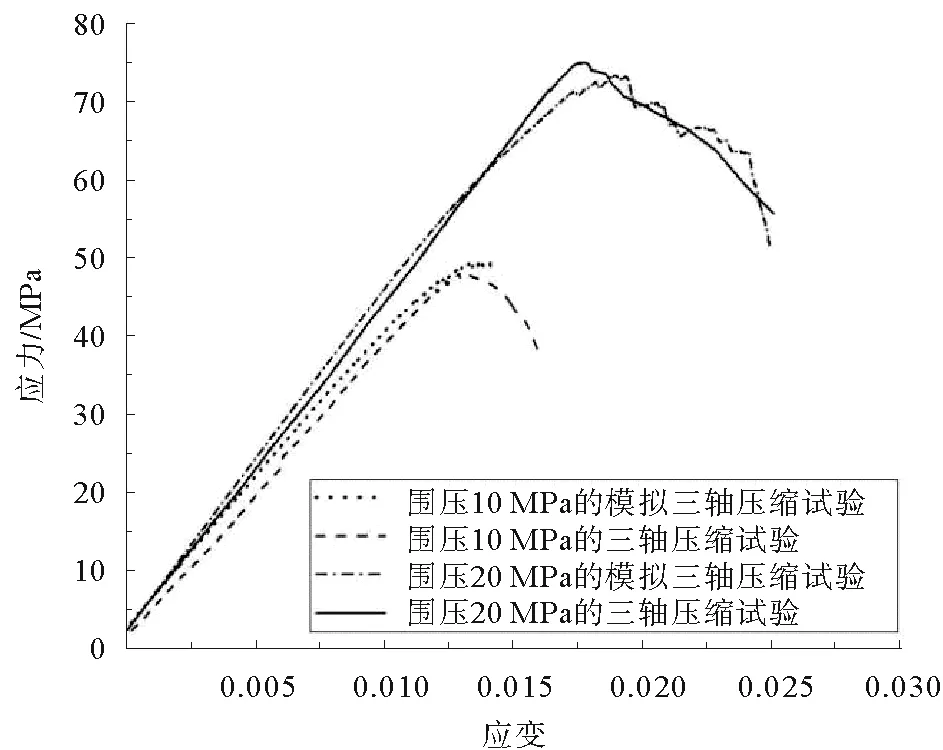
图5 三轴压缩及模拟试验应力-应变曲线对比Fig. 5 Comparison of stress-strain curves between triaxial compression and simulation test

表3 煤岩颗粒微观黏结参数Tab. 3 Micro bonding parameters of coal rock particles
2.3 煤岩截割模型的建立
根据滚筒截割半径R确定煤岩的宏观尺寸,长、高分别为800、1 300 mm,并由表2~3煤岩颗粒力学和黏结参数,建立煤岩宏观几何结构。根据式(2)及表1截割参数计算得到截齿截割表面。将镐型截齿外轮廓CAD图形导入PFC中,建立镐型截齿煤岩截割模型。为简化计算过程,模型建立过程中假设煤岩截割过程为单齿截割,且在截割过程中截齿无磨损;同时假设煤岩为均质煤岩,截割过程中煤岩受到镐型截齿截割作用发生脆性断裂,镐型截齿煤岩截割模型如图6所示,图中蓝色区域即为煤岩体。

图6 镐型截齿煤岩截割模型Fig. 6 Model of cutting coal rock of conical pick
3 镐型截齿煤岩截割过程仿真
表1中5种截割速度下,镐型截齿截割煤岩模拟过程大致相同。以表1序号1参数为例,其截割过程如图7所示。图7(a)~7(i)分别表示镐型截齿在接触到煤岩的瞬间及截割至7°、25°、50°、75°、90°、115°、140°、165°、180°时的煤岩破碎状态,绿色、红色分别为拉伸、剪切裂纹。由图7可知,在镐型截齿接触到煤岩瞬间,没有煤屑形成及脱落,而齿尖周围出现极少量拉伸、剪切裂纹;截割至25°时,有少量煤屑及裂纹形成;截割至50°~90°阶段时,大量的小块煤屑形成并崩落,出现大量拉伸、剪切裂纹;截割至115°~180°阶段时,出现大量大块煤屑及拉伸、剪切裂纹。综上可知,镐型截齿截至0°~90°阶段时,形成的煤屑以小块为主;当镐型截齿截过90°后,形成的煤屑以大块为主。
4 不同截割速度的镐型截齿截割力
4.1 截割力在截割过程中的变化
表1中5种截割速度时镐型截齿截割力在截割过程中的变化如图8中黑色线所示。在接触煤岩瞬间产生一个超过4 kN(图8中4 kN以上数据未显示)的大幅脉冲,在整个截割过程中呈无规则波动,与文献[16]单齿截割试验中截割力波动频率相似;对截割力曲线进行二阶拟合(红色曲线),拟合曲线在不同截割速度的变化趋势与文献[17]一致。进一步分析图8可发现,在截齿截割至约90°之后,频繁出现局部截割力明显降低的特点,推测其原因可能是在T/4时刻前后截割速度明显下降,造成煤屑在脱落前产生堆积,当大块煤屑脱落时,截割力出现明显的降低现象。

图8 截割力在不同截割速度截割过程中的变化Fig. 8 Changes of cutting force with various cutting speeds in the cutting process
4.2 不同截割速度时截齿截割力的统计
忽略镐型截齿接触煤岩瞬间产生的大幅脉冲,统计不同截割速度的截割力变化,见表4。由表4可知,当牵引速度、滚筒角速度最大时,镐型截齿在截割过程中的截割力均值、峰值及波动分别最大、最小。
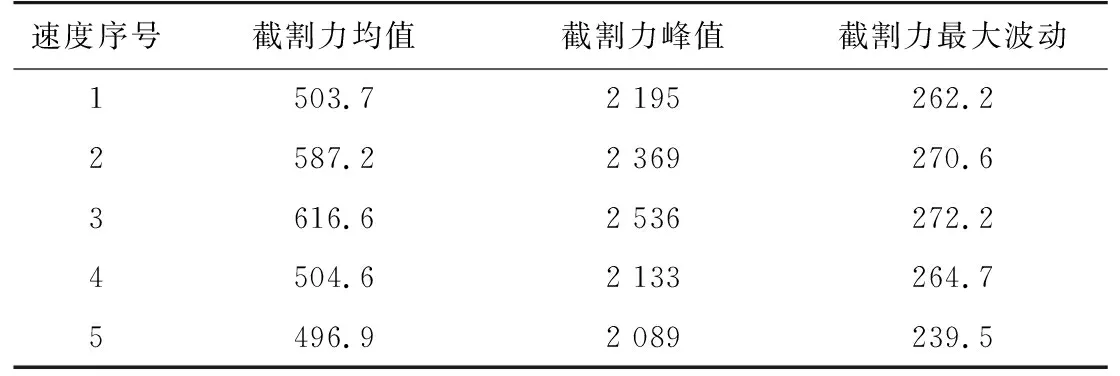
表4 不同截割速度截割过程中的截割力统计Tab. 4 Statistics of cutting force with various cutting speeds in the cutting process N
由表4中序号1、2、3截割力统计参数可知,滚筒角速度一定时,截割力均值、峰值及最大波动均随牵引速度的增加而增大。由表4中序号4、1、5截割力统计参数可知,牵引速度一定时,截割力均值及其最大波动均随滚筒角速度的增大而减小,其峰值呈无规律波动,但相差不大。由此可知在一定牵引速度下,提高滚筒角速度可改善截齿的受力情况。
5 不同截割速度的裂纹数量生成
5.1 裂纹数量在截割过程中的变化
表1所示5种截割速度时生成的裂纹数量在截割过程中的变化如图9所示。由图9可知,拉伸、剪切裂纹在不同截割速度的截割过程中均近似线性增加,且拉伸裂纹数量波动更为明显。进一步分析图9可知,当牵引速度、滚筒角速度分别增大时,镐型截齿煤岩截割过程中的拉伸、剪切裂纹数量的波动分别增多、减少。

图9 裂纹数量在不同截割速度截割过程中的变化Fig. 9 Changes of crack number with various cutting speeds in the cutting process
5.2 不同截割速度时生成裂纹数量统计
统计不同截割速度截割过程中的裂纹数量变化,见表5。由表5可知,当牵引速度、滚筒角速度最大时,在镐型截齿截割过程中生成的裂纹数量分别最大、最小。
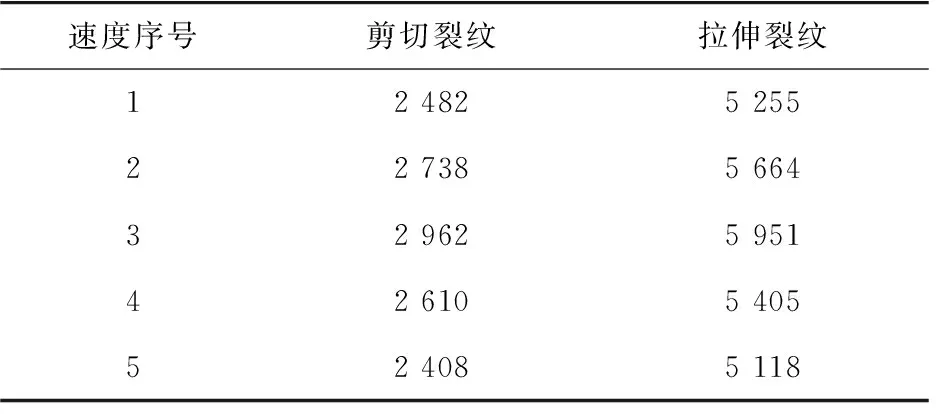
表5 裂纹数量在不同截割速度截割过程中的统计Tab. 5 Statistics of crack number with various cutting speeds in the cutting process
由表5中序号1、2、3裂纹数量统计可知,滚筒角速度一定时,拉伸、剪切裂纹数量均随牵引速度的增大而增加。由表5中序号4、1、5裂纹数量统计可知,牵引速度一定时,拉伸、剪切裂纹数量均随滚筒角速度的增大而减小。
结合表4中序号1、2、3及表5中序号1、2、3推断,随牵引速度的线性增加,截割力均值及产生的裂纹数量均非线性增加,截割比能耗也随之呈非线性减小趋势。
6 结论
主要研究了镐型截齿截割速度对煤岩截割过程的影响,主要考虑牵引速度、滚筒角速度对截割速度的影响,利用PFC建立不同截割速度的煤岩截割模型,模拟镐型截齿煤岩截割过程。得出如下结论:
1) 镐型截齿在截割过程中,其截割速度总体呈非线性减小趋势。滚筒角速度一定时,随牵引速度的增大,截割速度的非线性减小趋势增强;牵引速度一定时,截割速度随滚筒角速度的增大而明显增大。
2) 镐型截齿截割过程中截割力均值、峰值及最大波动均随牵引速度、滚筒角速度的增加分别增大、减小。在一定牵引速度下,提高滚筒角速度可改善截齿的受力情况。
3) 截割过程中产生的拉伸、剪切裂纹均随牵引速度、滚筒角速度的增加分别增大、减小,且截割力均值及产生的裂纹均随牵引速度的线性增加而呈非线性增加。滚筒角速度一定时,增大牵引速度可降低截割比能耗。
