巧用网格求锐角三角函数值
2022-02-16陈俊
陈俊

我们常常在网格图中利用垂直、平行关系构造直角三角形,通过勾股定理等方法求出任意两个格点间的距离来解决锐角三角函数值问题。
一、连接关键格点,构造直角三角形
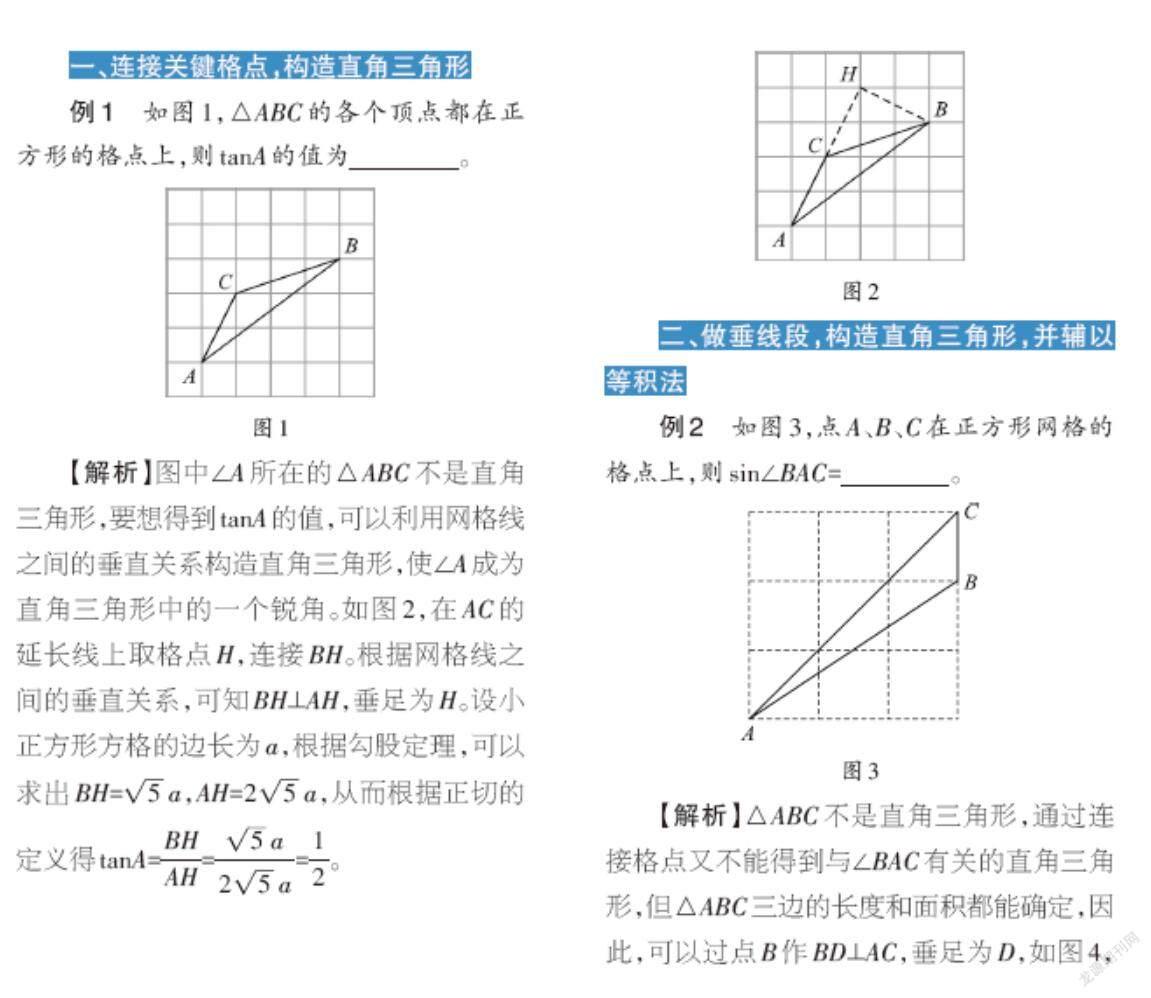
例1 如图1,△ABC的各个顶点都在正方形的格点上,则tanA的值为 。
【解析】图中∠A所在的△ABC不是直角三角形,要想得到tanA的值,可以利用网格线之间的垂直关系构造直角三角形,使∠A成为直角三角形中的一个锐角。如图2,在AC的延长线上取格点H,连接BH。根据网格线之间的垂直关系,可知BH⊥AH,垂足为H。设小正方形方格的边长为a,根据勾股定理,可以求出BH=[5a],AH=[25a],从而根据正切的定义得tanA=[BHAH]=[5a25a]=[12]。
二、做垂线段,构造直角三角形,并辅以等积法
例2 如圖3,点A、B、C在正方形网格的格点上,则sin∠BAC= 。
【解析】△ABC不是直角三角形,通过连接格点又不能得到与∠BAC有关的直角三角形,但△ABC三边的长度和面积都能确定,因此,可以过点B作BD⊥AC,垂足为D,如图4,则∠ADB=90°。根据△ABC面积的两种不同的表示方式,可以求出垂线段BD的长,从而在Rt△ABD中求出sin∠BAC的值。
设小正方形方格的边长为a,则根据勾股定理得AB=[(2a)2+(3a)2]=[13]a,由等积法可得BD=[22]a,所以在Rt△ABD中,sin∠BAC=[BDAB]=[22a13a]=[2626]。
三、通过图形平移,进行等角转化
例3 如图5,在正方形方格纸中,每个小的四边形都是相同的正方形,A、B、C、D都在格点处,AB与CD相交于点O,则tan∠BOD的值等于 。
【解析】∠BOD不是某一直角三角形的锐角,顶点O也不是格点,不满足利用定义求锐角三角函数值的条件。根据平移的性质,我们可以平移CD到C′D′,C′D′与AB交于点O′,如图6所示,平移后,∠BO′D′=∠BOD,且O′在格点上,这样tan∠BOD=tan∠BO′D′。
设小正方形的边长为a,则O′B=[5]a,O′D′=[22]a,BD′=3a,O′F=2a。
过点B作BE⊥O′D′,垂足为E。利用等积法,得S△BO′D′=[12]·BD′·O′F=[12]·O′D′·BE,则BE=[322]a。
由勾股定理,得O′E=[O′B2-BE2]=[22]a,
∴tan∠BO′E=[BEO′E]=[322a22a]=3,
∴tan∠BOD=tan∠BO′E=3。
本题通过平移CD,将原问题进行转化,然后利用等积法和勾股定理求出关键线段的长,再根据三角函数的定义求解。
在网格中求锐角三角形函数值,关键是利用锐角边上的格点找到直角三角形或构造直角三角形来进行求解。当锐角所在的三角形是直角三角形时,根据锐角三角函数的定义就可以直接求解;若锐角所在的三角形是非直角三角形时,常需要通过作垂线、平移线段等方式构造直角三角形,并辅以等积法求关键线段来解决。
(作者单位:江苏省南京外国语学校方山分校)
