“平面图形的认识（一）”常见错误解析

裴玲燕

平面图形的认识（一）是对平面图形的初步探索。在学习本章时，同学们容易出现概念、性质理解不清，线段、角度计算考虑不全面，漏解等错误。下面列出一些易错题，希望同学们能引以为戒。

一、概念、性质理解不清

1.下列说法正确的是（ ）。

A.延长射线AB到C

B.若AM=BM，则M是线段AB的中点

C.两点确定一条直线

D.过三点能作且只能作一条直线

本题考查了直线、射线和线段。熟练掌握相关概念和性质是解题的关键。我们要注意下列概念：直线是点在空间内沿相同或相反方向运动的轨迹，向两个方向无限延伸;过两点有且只有一条直线;直线上的一点和它一旁的部分所组成的图形称为射线，可向一方无限延伸。

A.射线本身可以无限延伸，不需延长，原说法错误;

B.若AM=BM，此时点M在线段AB的垂直平分线上，原说法错误;

C.两点确定一条直线，原说法正确;

D.只有三点共线时才能作一条直线，原说法错误。

2.下列说法：①两点确定一条直线;②两点之间，线段最短;③若AB=BC，则点B是线段AC的中点;④若∠1+∠2=180°，则∠1与∠2互为补角;⑤连接两点之间的线段叫作两点间的距离。其中正确的有（ ）。

A.1个 B.2个

C.3个 D.4个

本题出错原因是同学们不理解直线的性质、中点、补角、两点间的距离等知识，也就是对概念不清楚。熟练掌握这些基础知识是解题的关键。

①过两点有且只有一条直线，原说法正确;

②两点之间，线段最短，原说法正确;

③若AB=BC且三点共线，则点B是线段AC的中点，原说法错误;

④若∠1+∠2=180°，则∠1与∠2互为补角，原说法正确;

⑤连接两点的线段的长度叫作两点间的距离，原说法错误。

故说法正确的有3个。

二、线段、角度计算考虑不全面

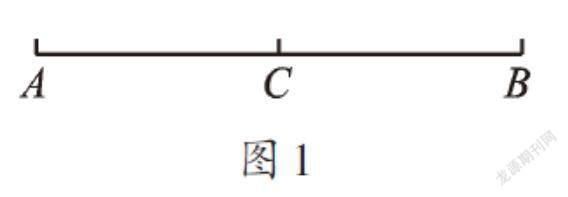
3.已知：如图1，线段AB=10，C是AB的中点。（1）求线段BC的长;（2）若点D在直线AB上，BD=2.5，求线段CD的长。

本题考查了两点间的距离。在求线段的长度时，若没有给出图形，则要注意分类讨论;若给出图形，就不需要分類讨论了。

（1）∵线段AB=10，C是AB的中点，

∴BC=AC=5。

（2）当点D在线段AB上时，

∵BC=5，BD=2.5，

∴CD=BC-BD=2.5;

当点D在线段AB的延长线上时，

∵BC=5，BD=2.5，

∴CD=BC+BD=7.5。

综上所述：线段CD的长为2.5或7.5。

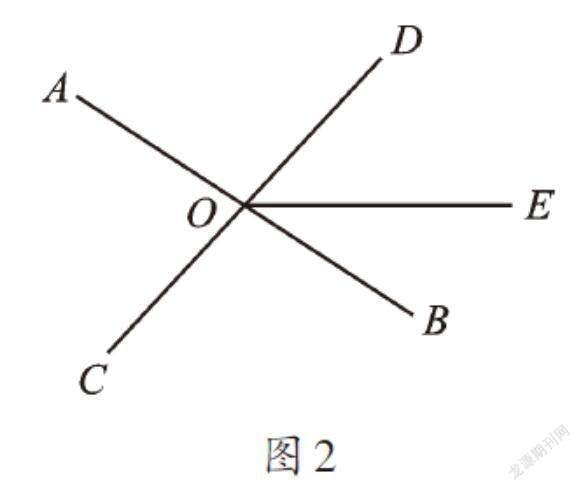
4.如图2，直线AB、CD相交于点O，已知∠AOC=80°，射线OE把∠BOD分成两个角，且∠BOE∶∠EOD=3∶5。（1）求∠BOE的度数。（2）过点O作射线OF⊥OE，求∠BOF的度数。

本题考查了对顶角相等的性质、角的计算，熟记概念并准确识图是解题的关键。这里射线OF有两种可能，即OF可能在∠AOD的内部，也可能在∠BOC的内部。

（1）∵∠AOC=80°，∠BOD=∠AOC，

∴∠BOD=80°。

∵∠BOE∶∠EOD=3∶5，

∴∠EOB=80°×[38]=30°。

（2）∠BOF=60°或120°。

三、画图分析能力弱导致漏解

5.在直线AB上任取一点O，过点O作射线OC、OD，使OC⊥OD，当∠AOC=30°时，∠BOD的度数是 。

在解没有给出图形的几何题时，我们需要考虑图形的所有可能，确保不重不漏。由于题目没有明确给出OC、OD的位置，故需要分情况讨论。

①当OC、OD在直线AB同侧时，∠BOD=60°;

②当OC、OD在直线AB异侧时，∠BOD=120°。

（作者单位：江苏省常州市新北区新桥初级中学）