2021年高考试题数学建模素养考查情况探析

吴凌菲 胡典顺

摘    要：数学建模是连接数学世界和现实世界的桥梁，是高中数学的六大核心素养之一.基于综合难度模型，从情境、运算、推理、建模工具和建模层次五个维度，对2021年高考全国甲卷（理科）、全国乙卷（理科）、新高考Ⅰ卷和新高考Ⅱ卷考查数学建模素养的试题进行统计与分析，有助于明确高中阶段对学生数学建模素养的培育程度.而采用融合试题与情境以发展学生应用意识、整合知识主题以建构完整知识体系、设置创新型情境以展现建模完整过程三个策略，可以有效考查并提升学生的数学建模素养.

关键词：2021年高考数学试题;数学建模;素养考查

高考作为我国选拔人才的主要方式，其作用不应局限于检测学生对理论知识的掌握情况，还应考查学生是否能够灵活运用所学知识，解决实际生活中的问题. 《普通高中数学课程标准（2017年版2020年修订）》（以下简称“《课程标准》”）提出了高中数学的六大核心素养——数学抽象、逻辑推理、数学建模、数学运算、直观想象和数据分析，并将“数学建模活动与数学探究活动”作为一个单独的主题，强调它是“高中阶段数学课程的重要内容”. PISA 框架也强调学生运用数学应对个人生活、职业生涯以及公民生活等情境中的问题的能力[1].因此，作为连接数学世界和现实世界的桥梁，数学建模理应受到足够的重视.以下，笔者从数学建模素养的角度对2021年高考数学全国甲卷（理科）（以下简称“全国甲卷”）、全国乙卷（理科）（以下简称“全国乙卷”）、新高考Ⅰ卷、新高考Ⅱ卷这四套试卷（以下简称“四套试卷”）进行分析，以期得到一些启示.

一、分析框架的建立

《课程标准》从情境与问题、知识与技能、思维与表达、交流与反思四个方面将学生的数学建模素养分为三个水平，但没有提供评价试题中数学建模素养水平考查的方式.因此，笔者根据《课程标准》对数学建模素养的阐述，参考鲍建生提出的试题综合难度模型，即用探究、背景、运算、推理、知识含量五个因素分析数学题目[2]，提炼出五个分析试题的维度——情境、运算、推理、建模工具和建模层次，并对每个维度的不同水平赋予数值，进行量化分析.其中，运算和推理两个维度的水平划分与鲍建生综合难度模型一致，故不再赘述.下面具体介绍情境、建模工具和建模层次三个维度的水平划分依据.

（一）情境维度的划分

由于数学建模是围绕现实问题进行的，故本文根据PISA框架对情境的划分，将情境维度分为个人、职业、社会和科学四种.个人情境与学生的日常生活关系密切，是学生最为熟悉的情境.职业情境聚焦劳动，涉及测量、成本计算、调度库存、工作决策等学生难以亲历的问题[3].社会情境基于社会公共生活，包括投票、公共交通、公共政策等一系列活动.科学情境着眼于自然科学领域，例如气候、生态、医学等，往往出现学生难以理解的理论知识，最不贴近学生的实际生活.根据学生对以上四种情境的熟悉程度，笔者分别对个人情境、职业情境、社会情境、科学情境的水平赋值1，2，3，4.

（二）建模工具维度的划分

基于高中数学的五大主题——预备知识、函数、几何与代数、概率与统计、数学建模活动与数学探究活动，结合高中数学建模可能使用到的数学理论知识，笔者将建模工具划分为几何，不等式、函数与方程，数列，导数，概率与统计五个子维度.由于知识本身的难易程度难以划分，所以对每个子维度的水平赋值均为1，并根据试题涉及的建模工具的数量进行累加赋值.

（三）建模层次维度的划分

学生的数学建模素养可以通过解题过程反映出来，不同难度的试题也可以映射出要考查的素养水平.根据喻平对数学核心素养划分的三种水平——知识理解、知识迁移、知识创新，笔者将建模层次分为理解模型、应用模型、建构模型，分别赋值1，2，3.其中，理解模型指的是考查学生能否直接调用曾经学过的、熟悉的模型解决简单的数学问题，应用模型指的是考查学生能否筛选出合适的模型解决需要运用多种知识的常规性问题，建构模型指的是考查学生能否灵活运用或组织所学的定理、公式、法则等建构新的数学模型来研究问题、解决问题并进行模型检验.

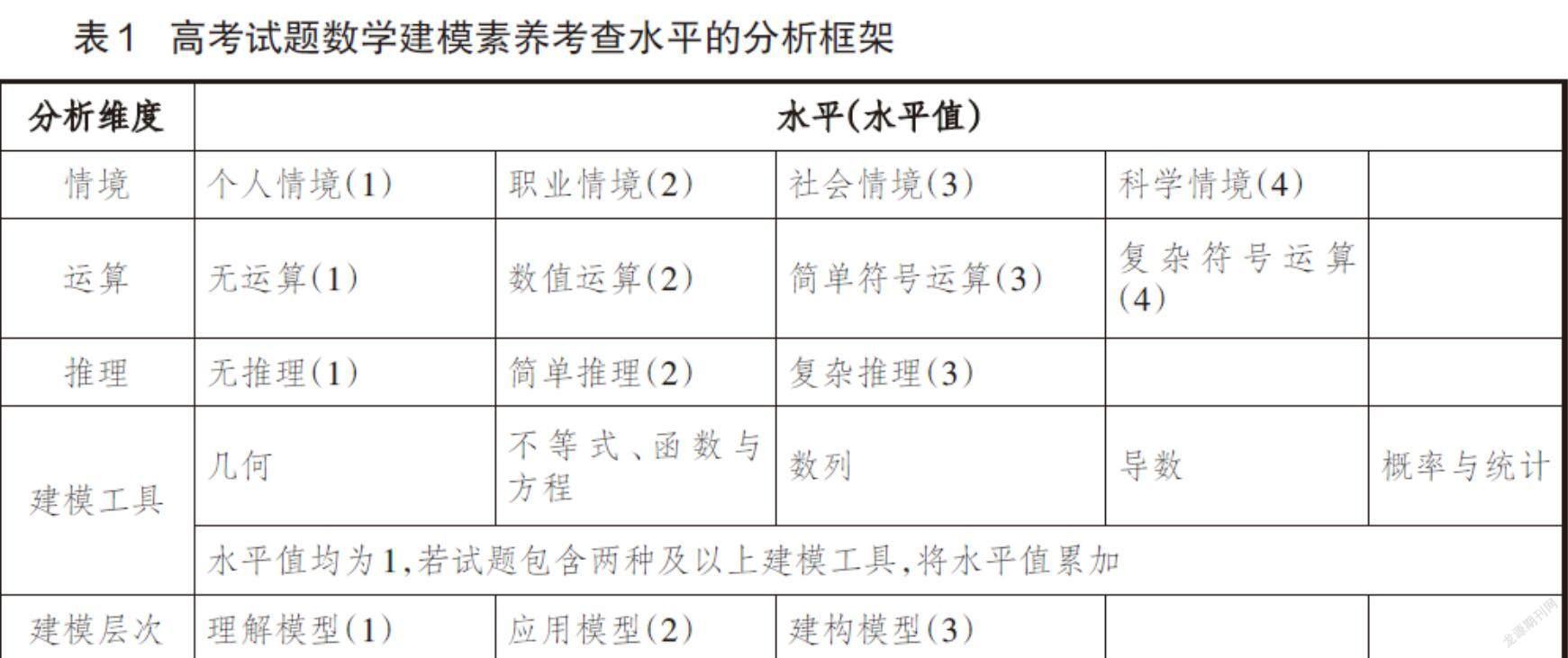
综合上述分析，可以得到2021年高考数学试题所考查的数学建模素养水平的分析框架，如表1.本文采用以下方法计算整套试卷某一维度的总体水平值：[di=jnijdijn]，其中，[di]代表第[i]维度的总体水平值，[nij]代表第[i]维度第[j]水平的试题数量，[dij]代表第[i]维度第[j]水平的賦值，[n]代表数学建模试题总数.

二、数据统计与分析

（一）数学建模试题统计

筛选四套高考试卷中考查数学建模核心素养的试题，统计试题题型、情境、分值等信息，得到表2.

根据表2可知，四套试卷中考查数学建模素养的试题的总分占比差距不大，但其占比总体来说都偏小，新高考Ⅰ卷更少.从试题类型上看，数学建模试题集中在选择题，且每套试卷都会有一道解答题考查学生对数学知识的应用能力.从试题情境上看，数学建模试题涵盖了个人情境、社会情境、职业情境和科学情境，大多以实际生活为背景，也有部分试题与数学史有关，如全国乙卷考查《海岛算经》中的测量方法.

（二）数学建模素养的考查水平

根据表1的分析框架对表2中的试题进行统计，可得到表3.需要说明的是，由于一道试题可能涉及多种建模工具的使用，对某一试卷使用某一类型的建模工具的试题数量所占百分比采用如下计算方式：[pj=mjjmj×100%]，其中[pj]代表使用第[j]种建模工具的试题数量所占百分比，[mj]代表第[j]种建模工具使用的次数.

下面根据表3的统计结果，对四套试卷在情境、运算、推理、建模工具、建模层次五个维度进行对比分析，最后对各维度的总体水平值作对比说明.

1.情境维度

由于考查数学建模素养的试题在试卷总题量中占比不高，四套试卷均只涉及两类或三类情境.全国甲卷和乙卷的情境集中在职业情境，而新高考Ⅰ卷和Ⅱ卷的情境则相对分布得更加均匀.具体而言，个人情境仅出现在全国甲卷，科学情境仅出现在新高考Ⅱ卷.四套试卷均涉及职业情境，考查的背景多以测量和产品质量的比较为主.除全国甲卷外，其他三套试卷均含有社会情境的试题，以我国社会经济发展与科技进步的重大成就为素材，例如新高考Ⅰ卷中的“一带一路”知识竞赛，在考查学生的数学建模素养的同时，引导学生关注社会发展，增强民族自豪感和自信心.

2.运算维度

四套试卷数学建模试题考查的运算能力均只涉及中间两个水平，不涉及无运算和复杂符号运算的试题，整体来说运算难度中等.相对而言，全国甲卷和新高考Ⅱ卷有更多的试题考查简单符号运算，而全国乙卷和新高考Ⅰ卷则更多地涉及数值运算，运算难度偏低.

3.推理维度

四套试卷数学建模试题在推理维度上表现出一致性，基本上以简单推理为主，对学生的逻辑推理能力要求不高，极少数试题处于复杂推理水平，没有不需要推理的试题.全国甲卷、全国乙卷和新高考Ⅰ卷的建模类试题仅考查简单推理，新高考Ⅱ卷则有33.33%的试题考查了复杂推理.

4.建模工具维度

四套试卷的数学建模试题涵盖了五种类型的建模工具，但它们所占的比例有明显差别.概率与统计模型的试题出现次数最多，每套试卷均有所涉及，不等式、函数与方程模型次之，在三套试卷中出现，几何、数列、导数模型虽有出现但占比较少.具体来看，全国甲卷和新高考Ⅱ卷涉及的模型类型有三种，比全国乙卷和新高考Ⅰ卷多.全国甲卷第8题考查学生能否正确运用线线关系、线面关系等几何知识将已知量转化到一个三角形中，涉及几何模型的应用，新高考Ⅰ卷第16题计算对折后的图形面积之和涉及数列模型的应用，新高考Ⅱ卷第21题考虑函数的单调性涉及导数模型的应用.概率与统计模型的试题涉及的知识点非常丰富，全国甲卷考查排列组合、频率的计算和独立性检验，全国乙卷考查平均数与方差的计算和应用，新高考Ⅰ卷考查随机变量的分布列和期望的应用，新高考Ⅱ卷考查正态分布和随机变量的分布列.不等式、函数与方程模型的试题存在和其他模型交汇考查的情况，例如新高考Ⅱ卷第21题需要学生综合运用概率与统计，不等式、函数与方程以及导数的知识，这与函数在高中数学的核心地位密不可分.

5.建模层次维度

总体上看，四套试卷的数学建模试题考查的建模层次处于中等水平，其中，理解模型和应用模型的试题占比最高，建构模型只出现在新高考Ⅱ卷中.全国甲卷以理解模型为主，例如第4题给出了具体的对數线性模型，用于描述五分记录法数据和小数记录法数据的关系，学生只要能读懂题意，将数值代入表达式即可.全国乙卷以应用模型为主，例如第6题考查分组分配问题，需要学生明确题目为不等分组的分配问题，应该先分组后排列.新高考Ⅰ卷在理解模型、应用模型两个水平分布均匀，新高考Ⅱ卷则在理解模型、应用模型、建构模型三个水平分布均匀.值得关注的是，反映建构模型水平的试题，不仅考查了学生将情境问题表达成数学问题的能力，还考查学生能否根据生命科学的真实情境对给出的数学结果作出解释的能力，较之其他试题能更完整地体现数学建模的过程，展现数学的应用之美，让学生体会理论与实际结合之妙.

6.各维度总体水平值

依据表3，可以得到四套试卷数学建模素养不同维度考查的总体水平值（图略）.新高考Ⅱ卷考查的数学建模素养水平在五个维度都相对最高，新高考Ⅰ卷与全国乙卷考查的素养水平相差不大，全国甲卷在情境、建模层次、推理维度上考查水平偏低，建模工具维度上考查水平居中，运算维度上考查水平相对较高.但简而言之，四套试卷各维度的水平都没有保持一个近似平衡的五边形，在建模工具和建模层次维度考查的水平偏低.究其原因，除了新高考Ⅱ卷第21题融合了三种建模工具以及全国甲卷第8题涉及两种建模工具的使用外，其他试题都仅仅考查学生单一主题的模型使用能力，并且大约一半的试题呈现了解题所需的模型.

为了进一步分析四套试卷考查的整体的数学建模素养水平，可以根据公式[d=idiki]对各维度的水平值进行加权平均.其中，[ki]代表第[i]维度所占的权重，以“情境”权重为1.00作为参考标准，各维度所占权重依次为1.00，1.19，1.53，0.91，1.35[4].将表3中的数据代入公式，得到全国甲卷、全国乙卷、新高考Ⅰ卷、新高考Ⅱ卷考查的数学建模素养的综合水平分别为10.91、11.33、11.47、13.96.由此，可以更直观地看出四套试卷考查的数学建模素养水平从高到低依次为新高考Ⅱ卷、新高考Ⅰ卷、全国乙卷、全国甲卷.

三、结论与启示

（一）结论

从整体上看，全国甲卷、全国乙卷、新高考Ⅰ卷和新高考Ⅱ卷考查数学建模素养的试题均只有2～3题，占试卷总分值的11.33%～14.67%，四套试卷数学建模素养的综合考查水平从高到低依次为新高考Ⅱ卷、新高考Ⅰ卷、全国乙卷、全国甲卷，但总体来说考查的内容都比较基础，不会使学生产生对数学建模试题的畏难情绪.从情境的角度看，四套试卷涵盖了PISA框架的四种情境，职业情境和社会情境相对较多，几乎每套试卷都有这两种情境.从运算的角度看，四套试卷的数学建模试题都仅涉及数值运算和简单符号运算，运算难度处于中等水平.从推理的角度看，试题的推理难度不高，大多处于简单推理水平，需要复杂推理的试题很少.从建模工具的角度看，概率与统计模型的试题占比最大，不等式、函数与方程模型次之，其他模型出现频率很低，并且大多数试题都只涉及一种类型的模型的使用.从建模层次的角度看，四套试卷对学生建模能力的要求不高，绝大多数试题考查的是学生能否理解模型和应用模型.

（二）启示

1.融合试题与情境，发展学生的应用意识

一方面，高考命题以数学核心素养为导向，情境的设计直接影响着数学核心素养的有效评价，数学建模核心素养作为六大数学核心素养之一，对其素养水平的评价与情境的复杂程度、真实程度密切相关[5].另一方面，数学建模过程需要将现实问题抽象为数学问题，将数学结果解释成现实结果，依赖具体情境的建构.因此，在高考数学试卷中绝大多数试题都是无情境试题的情况下，可以适当增加情境化的试题.在试题中融入情境，可以根据学生的认知发展情况选取学生熟悉的材料，例如社会经济发展过程中的热点问题、我国古代优秀的传统文化、简单的学科交叉问题等，对其加以利用、改编，不仅可以考查学生对真实情境问题的解决能力，还可以开阔学生的视野，帮助学生感悟数学的独特魅力，增强学生用数学知识解决问题的意识.但需要注意的是，将试题与生活结合，不仅要关注情境的真实性，还要考虑情境与试题结合的有效性，不能出现脱离情境也可以解决问题的情况.

2.整合知识主题，建构完整的知识体系

希尔伯特曾说：“数学科学是一个不可分割的有机整体，它的生命力正是在于各个部分之间的联系.”数学知识之间存在深刻的内在联系，《2019年普通高等学校招生全国统一考试大纲（理科数学）》（2021年沿用）也指出，命题设计要围绕知识网络的交汇点，使对数学基础知识的考查达到必要的深度.教材中各章节内容相对独立，学生在知识学习的过程中也可能出现学后忘前、不能整合的情况，因此局限于考查学生对于某一类主题知识的应用能力，难以实现高考的选拔性要求.此外，相对于高考数学建模试题的情境，现实生活中需要运用数学知识解决的问题往往要复杂得多，因此，高考试题特别是数学建模试题，应考查学生的综合应用能力.通过试题的编制，将不同主题的知识联系起来，有助于学生系统、全面地理解数学知识，提高迁移数学知识的能力，以及分析、解决现实问题的能力.

3.设置创新型情境，展现建模完整过程

一个完整的数学建模过程包括将现实情境简化成现实模型，再将其数学化，形成数学模型，然后对数学模型进行求解得到数学结果，将数学结果解释成现实结果，再对现实结果进行检验并改进模型，如此循环，不断修正[6].在理想的情况下，一道结构良好的考查数学建模素养的试题，应涉及数学建模的全过程，但由于考试的局限性，数学建模试题往往聚焦于学生对数学知识的应用能力，以应用模型、求解模型为考试的重点.而让学生经历完整的数学建模过程，可以使学生积极思考、敢于质疑，培养数学思维和创新意识，积累数学活动经验，实现“用数学的眼光观察世界，用数学的思維思考世界，用数学的语言表达世界”的数学学习的最终目标.因此，考试试题的命制也应尽量考虑到数学建模的全过程，可以建构创新情境，每一题设置多个小问题，分别对应数学建模的每个子过程，从而更加有效地考查学生的数学思维和数学建模能力.考虑到数学建模的开放性，还可以设置开放性试题，适当渗入一些需要学生作出判断的不确定性知识[7].

参考文献：

[1][3]于国文，陈鹏举，冯启磊，等.PISA数学测评内容和情境演变及其启示[J].数学教育学报，2019（4）：17-23.

[2]鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望，2002（9）：48-52.

[4]武小鹏，张怡.中国和韩国高考数学试题综合难度比较研究[J].数学教育学报，2018（3）：19-24，29.

[5]常磊，鲍建生.情境视角下的数学核心素养[J].数学教育学报，2017（2）：24-28.

[6]BLUM W， LEI D. How Do Students and Teachers Deal with Modelling Problems？[A]. HAINES C. et al.Mathematical Modelling： Education，Engineering and Economics. Chichester： Horwood， 2007：225.

[7]喻平.发展学生学科核心素养的教学目标与策略[J].课程·教材·教法，2017（1）：48-53.