周期性基础地震波衰减性能及其试验验证
2022-02-15赵春风MO
赵春风,曾 超,MO Y L
(1.合肥工业大学土木与水利工程学院,安徽 合肥 230009;2.Department of Civil and Environmental Engineering,University of Houston,Houston 77051,USA;3.中国地震局工程力学研究所中国地震局地震工程与工程振动重点实验室,黑龙江 哈尔滨 150080)
引 言
基础隔震系统(橡胶支座和摩擦摆系统)是目前应用广泛并且较为实用的隔震方法。它通过在上部结构底部和基础顶面之间设置小刚度和高阻尼隔震系统,以减小结构的地震响应[1-2]。基础隔震系统已较为广泛地应用于房屋和桥梁等基础设施建筑中,然而传统基础隔震系统仍然存在水平位移大,无法竖向隔震,需设置隔震沟等问题[3-5]。因此亟需开发一种新型的隔震技术来克服上述困难。
固体物理学中的研究表明,某些频段的弹性波在周期性复合介质中传播时,由于Bragg 散射导致的相消干涉,使得该频段的弹性波无法穿过周期性结构,这些频率范围称为弹性波禁带。Kushwaha等[6]在研究镍-铝二维周期性复合介质时首次提出声子晶体概念,并指出声子晶体的滤波特性在构造无振动环境方面具有巨大潜力。Liu 等[7]通过在软性基体材料中嵌入铅制单元,突破传统质量定律,实现小尺寸控制大波长,极大地拓宽了声子晶体结构在低频研究领域的可设计性和应用范围。
基于声子晶体的带隙特性,研究者已经将周期性复合材料介质广泛应用于隔声降噪、声隐身、声学斗篷、热绝缘等工程物理器件的设计中[8-9],这些研究领域的频率范围主要覆盖kHz 到THz。如何利用声子晶体的滤波特性阻隔主要频率段为0.1~50 Hz的地震动,显然是一项充满挑战且有意义的研究。文献[10-11]率先将声子晶体的概念引入到土木工程领域,提出周期性隔震基础的设想,利用其带隙特性来阻隔水平和垂直方向上的地震波。Cheng 等[12]基于周期结构的方向衰减域特性,设计了一种复合周期性基础,并通过数值仿真验证其在核电厂结构隔震中实现多维衰减的可能。Witarto 等[13-14]和Zhao 等[15-16]通过数值分析和振动台试验,进一步探讨了一维和三维周期性基础的带通特性,设计并完成了含周期性基础的小型模块化反应堆模型试验。为周期性基础从理论设计、数值模拟走向实践提供了参考。
基于作者前期对周期性基础衰减域特性及其隔震性能的研究,本文利用橡胶和混凝土两种材料构造一维复合层状周期性基础。根据Bloch-Floquet理论推导理想一维周期性基础的频散方程,对比分析周期性基础和叠层橡胶支座隔震机理的差异。通过频域分析和瞬态分析,对含有一维周期性基础和普通钢筋混凝土基础的三层钢框架的衰减效果进行研究,并利用小型振动台试验进行验证。结果表明,外部激励频率处于周期性基础频率带隙内时,可以有效减小上部结构的动力响应。因此,通过调节周期性基础频率带隙宽度可使其覆盖地震波的主要频段。
1 一维层状周期性基础的理论解
根据各层介质在交界面处的位移和应力的连续性,并结合Bloch-Floquet 定理,利用传递矩阵法可得到理想一维层状周期性结构的频散关系,具体推导过程如下。
如图1(a)所示,考虑由两种均质、各向同性的弹性介质沿着z方向交替排布的一维周期性基础。为简化分析,假设基础在xoy平面内为无限大,两种材料在交界面处粘结完好,并忽略材料阻尼的影响。利用结构的周期特性,可只取一个典型单元进行分析[13-16]。如图1(b)所示,典型单元的两种材料厚度分别为h1和h2,单元总厚度为h=h1+h2。不失一般性,以xoy平面内沿着z方向传播、x方向振动的剪切波为例,分析一维层状周期性基础的频散特性。
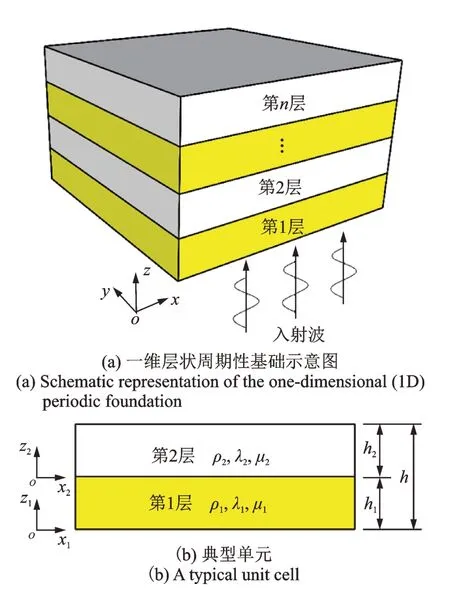
图1 n 层一维周期性基础及其典型单元Fig.1 1D periodic foundation and its unit cell with n layers
二维平面内弹性波波沿z方向在第n层介质中传播的波动方程为:

式中un和zn分别表示物质点在第n层介质中沿x方向的位移和局部坐标,Cn表示波速,t为时间。P波和S 波在第n层介质中的波速表示如下:
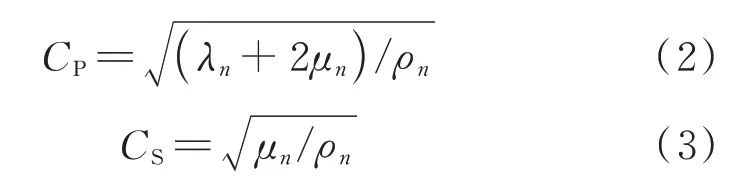
式中λn和μn称为Lame 系数,ρn表示第n层介质的密度。
根据Bloch-Floquet 定理,理想周期结构中波具有如下形式的解:
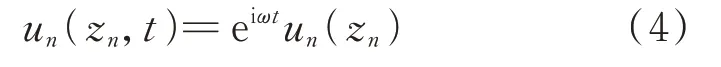
式中ω为角频率,i2=−1。
将方程(4)代入方程(1)得到关于un(zn)的二阶齐次微分方程,求解该微分方程得到第n层的位移为:
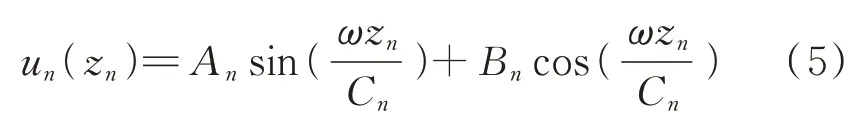
利用几何方程和物理方程得到第n层的剪应力为:
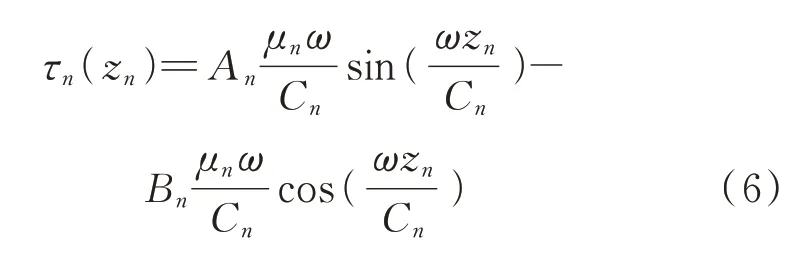
记Un(zn)=[un(zn),τn(zn)]T为状态函数向量,Ψn=[Kn,Qn]T为待定系数向量,联立方程(5)和(6),得到Un(zn)和Ψn的函数关系为:
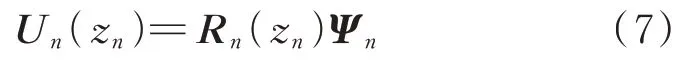
其中:

简记第n层介质底部和顶部的状态向量分别为和Ubn,则有:

式中Tn=Rn(zn)[Rn(zn)]−1称为第n层的传递矩阵,Tn起到将状态函数向量向下一层传播的作用。由于各层介质在交界面处的位移和应力是连续的,根据方程(9)可得:
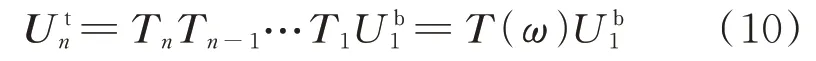
其中,典型单元的传递矩阵T(ω)为角频率ω的函数。
根据单胞的周期性,位移和应力在zn∈[0,h]是周期性重复的,由Bloch 定理有:

式中k为波数。联立式(10)和(11)有:
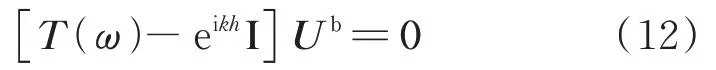
式中 I 为单位矩阵。方程(12)若有非零解,必须满足:
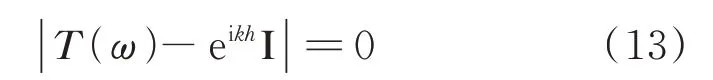
通过求解方程(13)可得到波数k和频率ω之间的关系,即频散关系。针对由两种材料组成的一维层状周期性基础,频散方程可化简为:
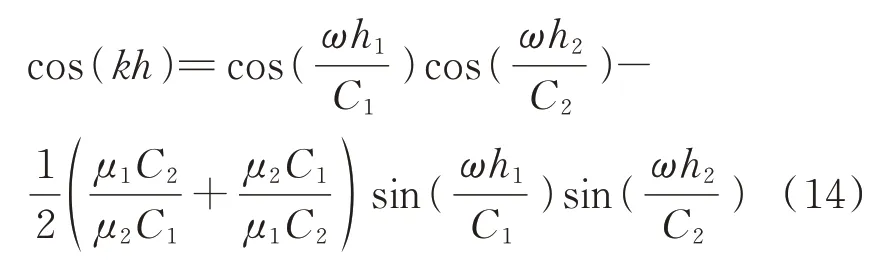
选择土木工程中常用的混凝土和橡胶两种材料构成一维层状周期性基础。混凝土的密度、杨氏模量和泊松比分别为2300 kg/m3,25 GPa,0.33,橡胶的物理参数对应为1300 kg/m3,147 kPa,0.463。根据前期预分析,选取混凝土层和橡胶层厚度均为0.2 m。通过扫描方程(13)中的波数k,即可得到一维层状周期性基础关于S 波的频散关系(见图2(a))。值得说明的是,第一布里渊区内的波数可对应周期结构中所有的波动模态,而第一布里渊区又可以通过对称操作获得最小不可压缩区域,称为第一不可约布里渊区。因此为了确定周期结构的带隙范围,任意波数k只需限制在第一不可约布里渊区边界,即k∈[−π/h,π/h]。同理,结合波动方程和周期性边界条件,扫描波数k,可获得一维层状周期性基础关于P 波的频散曲线(见图2(b))。
由图2(a)可知,S 波前三阶频率带隙分别是6.8~15.54 Hz,18.45~31.08 Hz 和32.75~46.62 Hz,P 波的第一带隙为25.93~59.21 Hz。这4 段频率带隙均处于较低频范围,基本位于地震波的主要频段(0.1~50 Hz),因此一维层状周期性基础有望用于工程结构的隔震减震。
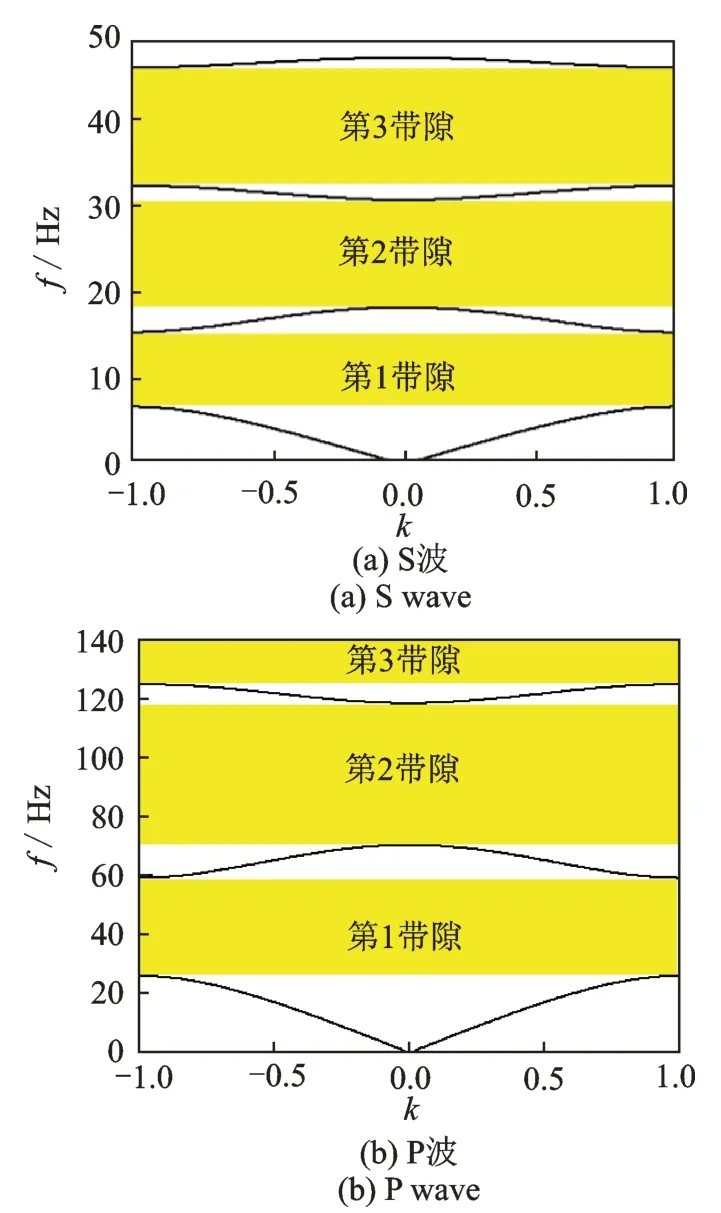
图2 一维周期性基础的频散关系图Fig.2 Dispersion curve of 1D periodic foundation
2 叠层橡胶隔震支座的频散特性
2.1 几何参数和物理参数
叠层橡胶隔震支座是由薄层橡胶和钢板交替叠加,通过橡胶硫化而成的一种隔震支座。本文中一维层状周期性基础的结构形式类似于叠层橡胶隔震支座。为了明确一维层状周期性基础与叠层橡胶隔震支座的隔震机理差异,有必要对叠层橡胶隔震支座的频散关系进行分析。
选取标准正方形叠层橡胶隔震支座,支座的几何参数如表1所示。钢板的密度、杨氏模量和泊松比分别为7850 kg/m3,205 GPa,0.28,橡胶的物理参数与第1 节相同。
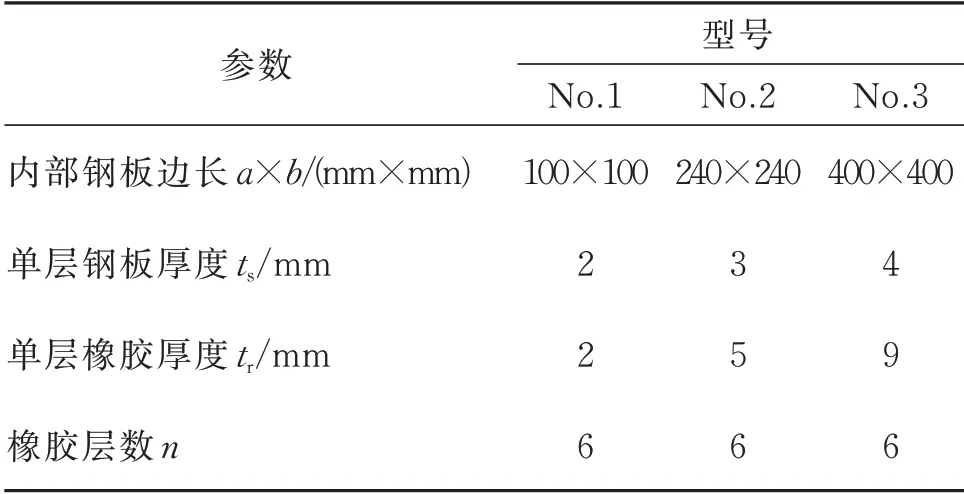
表1 标准叠层橡胶隔震支座Tab.1 Standard laminated rubber bearing
2.2 频率带隙
参考第1 节中的传递矩阵方法,可计算得到三种型号叠层橡胶隔震支座关于S 波的频散关系(如图3所示)。
由图3(a)可知,叠层橡胶隔震支座No.1 的前三阶频率带隙分别为391.58~1553.91 Hz,1651.88~3107.97 Hz和3159.39~4662.42 Hz。由图可知,叠层橡胶隔震支座No.1第一带隙的起始频率(391.58 Hz)远超过地震波的频率范围,即叠层橡胶隔震支座No.1 无法阻隔低频段(0.1~50 Hz)的地震波。同理,叠层橡胶隔震支座No.2 和No.3 的第一频率带隙分别为198.8~621.57 Hz 和126.42~345.27 Hz,也都远高于地震波的主要频段。
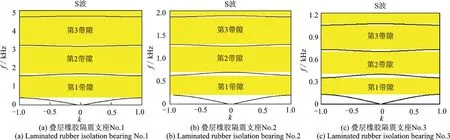
图3 叠层橡胶隔震支座频率带隙Fig.3 Frequency bandgap of the laminated rubber isolation bearing
上述分析表明,三种叠层橡胶隔震支座的频率带隙处于高频段,而地震波属于低频波。叠层橡胶隔震支座的减震机理应归结为:通过减小侧向刚度,延长结构自振周期,增加阻尼耗能来达到减小结构地震响应的目的。因此,无法利用叠层橡胶隔震支座的带隙特性来阻隔地震波,这与本文中的一维层状周期性基础隔震机理存在本质区别。
3 周期性基础动力响应数值分析
3.1 有限元模型
为了验证周期性基础的隔震效果,采用ANSYS 分别建立含有一维周期性基础(One Dimensional Periodic Foundation,1D PF)和固定基础(Fixed Foundation,FF)的三层钢框架有限元模型(Finite Element Model,FEM)并分析其动力特性。
一维层状周期性基础的平面尺寸为1 m(长)×1 m(宽),每层厚度为0.2 m,材料属性如第1 节所述。钢框架柱子为方形空心截面,截面尺寸为6 cm(宽)×6 cm(高)×0.32 cm(厚);矩形空心截面梁的截面尺寸为3 cm(宽)×6 cm(高)×0.32 cm(厚);楼板厚度为0.3 cm。钢框架每一层的高度是30 cm,平面尺寸为60 cm×60 cm,每层楼配重20 kg。如图4所示,具体的有限元模型采用BEAM188 单元模拟框架的梁和柱,SHELL163 单元模拟楼板,SOLID45 模拟周期性基础,MASS21 单元模拟附加质量。另外,由于SOLID 单元和SHELL 单元的节点自由度不一致,需要额外定义三个耦合方程来实现共节点。
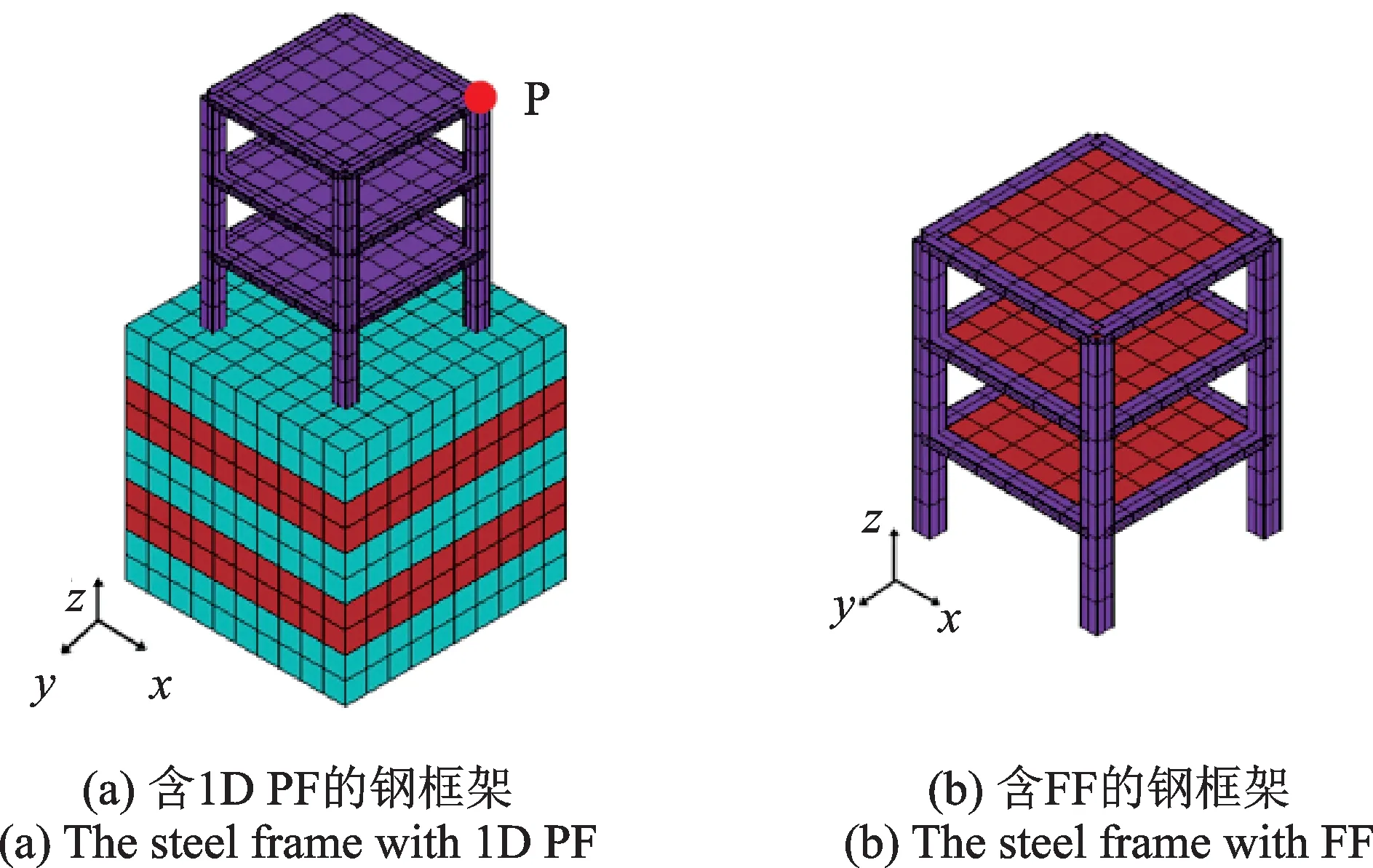
图4 含有不同基础的钢框架的有限元模型Fig.4 FEMs of steel frames with different foundations
3.2 频域分析
首先对含有一维周期性基础的钢框架有限元模型(FEM-PF)和直接固定在地基上的钢框架有限元模型(FEM-FF)进行频域分析。定义了频率响应函数(Frequency Response Function,RFRF)来衡量FEM-PF 动力响应的衰减效率[13-16]。频率响应函数的表达式为20lg(Ai/A0),其中Ai和A0分别是模型顶部P 点的位移幅值和输入谐波的幅值。为了模拟S 波的激励,固定基础其他方向约束,仅沿x方向输入幅值为A0频率为f的简谐波。通过扫描f,即可获得各个频段模型顶部P 点的位移响应。
由图5(a)可知FEM-FF 顶部P 点的RFRF值都大于0。这表明上部结构的位移响应大于输入的谐波位移幅值,即固定基础的上部结构动力响应增大。相反地,由于输入波的频率大部分位于周期性基础的频率带隙(6.8~15.54 Hz,18.45~31.08 Hz,和32.75~46.62 Hz)内部,FEM-PF 顶部P 点的RFRF值基本小于0;在0~6.8 Hz 频段(处于带隙外部)RFRF大于0。这表明周期性基础能有效阻隔频率带隙内的谐波,减小上部结构的动力响应。
同理,为了模拟P 波输入,固定基础其他方向约束,仅沿竖直z方向输入幅值为A0的简谐波,考查有无周期性基础的钢框架的动力响应。如图5(b)所示,当简谐波的输入频率处于周期性基础带隙(25.93~59.21 Hz,70.3~118.41 Hz)内部时,结构的动力响应明显降低。
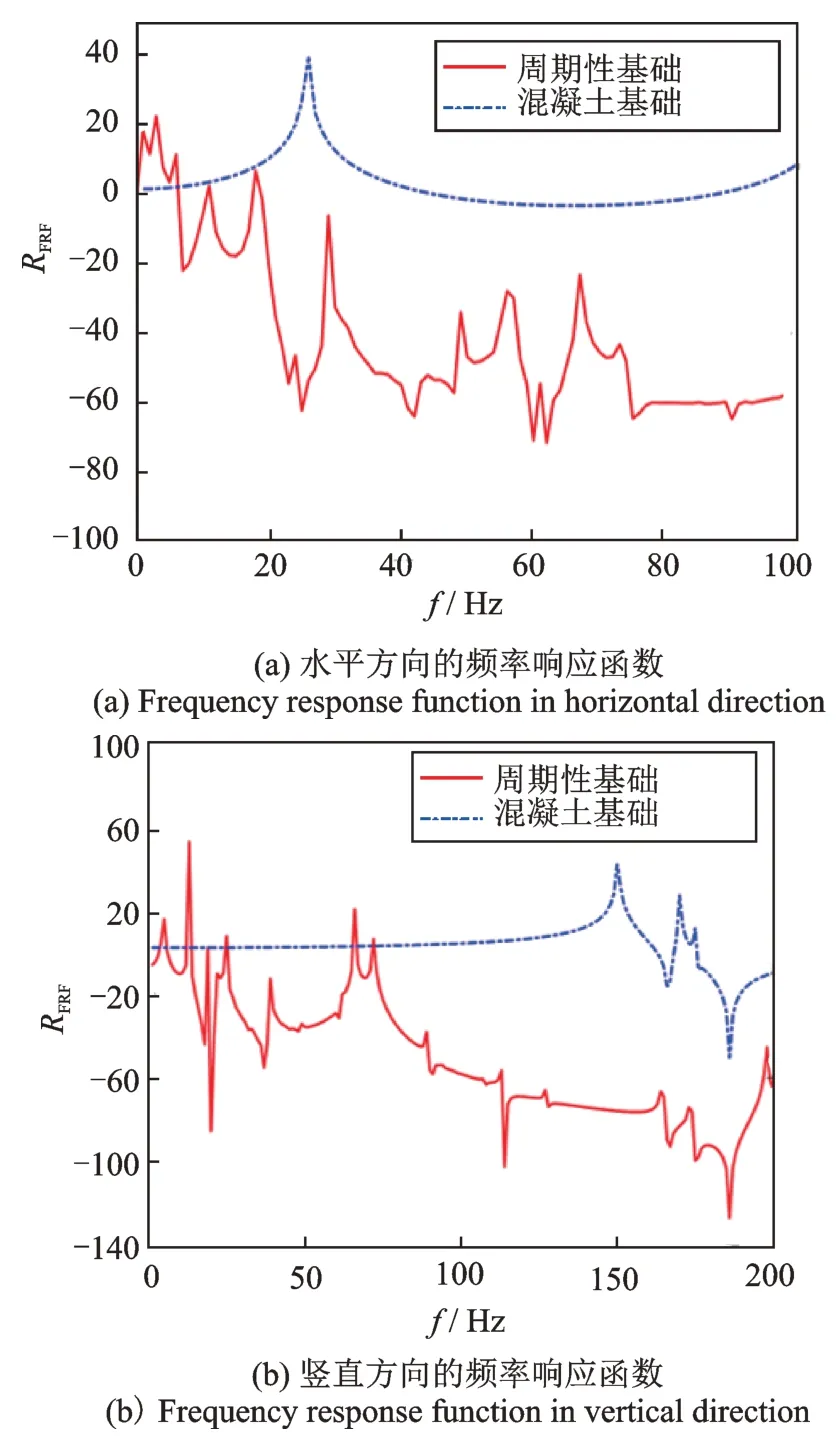
图5 上部结构顶点P 的频率响应函数Fig.5 Frequency response function of superstructure at point P
结果表明,当简谐波的频率处于周期性基础频率带隙内时,周期性基础对S 波和P 波均具有很好的阻隔作用。
3.3 瞬态分析
为了进一步验证周期性基础的带通特性,对FEM-PF 和FEM-FF 进行瞬态分析。选取Oroville,El-Centro 和Saguenay 三条水平向地震记录作为输入地震动[17],地震波的峰值加速度(Peak Ground Acceleration,PGA)均调整为1g,实际输入的地震波峰值调整为0.4g。下面分别分析三条地震波作用下,上部结构顶点P 的加速度响应。
3.3.1 Oroville 地震波
图6表示Oroville 地震波的加速度时程及其傅里叶谱。由图6(b)可知,地震波的主要频率(7~9 Hz)落在周期性基础的第一频率带隙(6.8~15.54 Hz)内。图7表示的是FEM-PF 和FEM-FF 钢框架顶部P 点沿水平x方向的加速度响应。由图可知,周期性基础钢框架P 点的峰值加速度是0.39g,而固定基础钢框架峰值加速度是0.61g,峰值加速度相对降低约36.1%。图8表示的是顶点P 的加速度反应谱。由图可知,地震波主频12.5 Hz 处于周期性基础的频率带隙内时,周期性基础可以有效地减小上部结构的加速度响应;相反,固定基础则增大了钢框架的加速度响应。
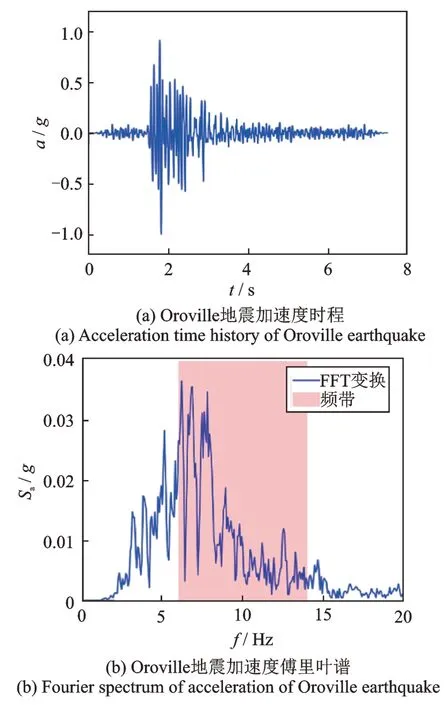
图6 Oroville 地震加速度时程及其傅里叶谱Fig.6 Acceleration time history and Fourier spectrum of Oroville earthquake
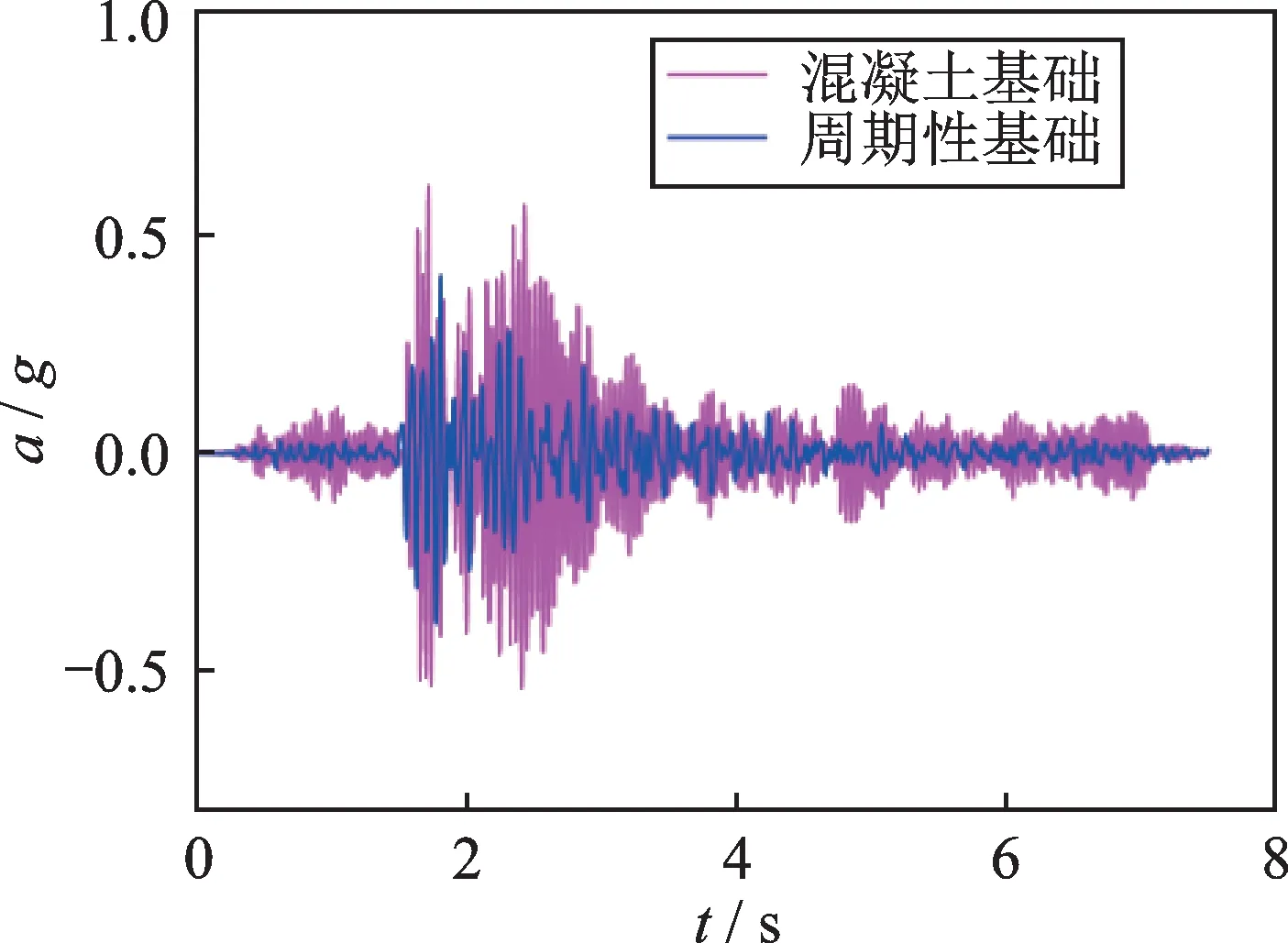
图7 Oroville 地震作用下有限元模型顶部的水平加速度响应Fig.7 Horizontal acceleration response at the top of FEM subject to Oroville earthquake
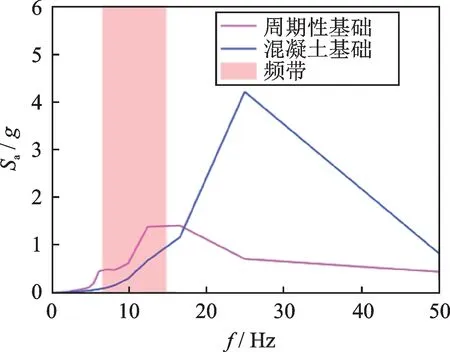
图8 Oroville地震作用下有限元模型顶部的水平加速度反应谱Fig.8 Horizontal acceleration response spectrum at the top of FEM subject to Oroville earthquake
3.3.2 El-Centro 地震波
图9是El-Centro 地震波加速度时程及其傅里叶谱。由图9(b)可知,El-Centro 地震波的主频(1~4 Hz)在周期性基础的频率带隙之外。图10表示El-Centro 地震波激励下有限元模型顶点水平方向加速度响应。不难发现,周期性基础上部结构的加速度响应大于固定基础上部结构的动力响应。类似地,周期性基础结构的加速度反应谱远大于固定基础的加速度反应谱(如图11所示)。
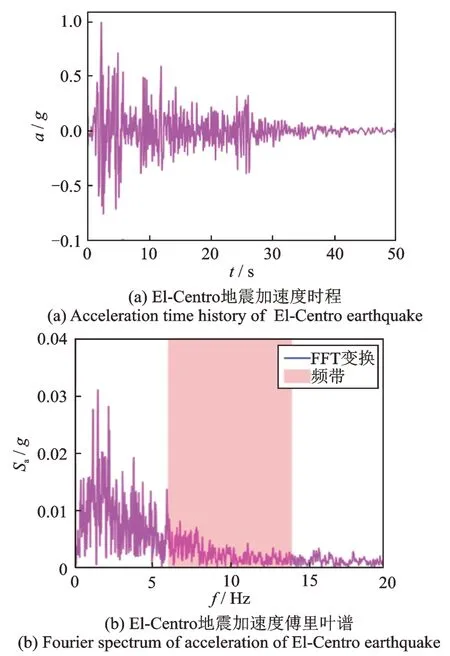
图9 El-Centro 地震加速度时程及其傅里叶谱Fig.9 Acceleration time history and Fourier spectrum of the El-Centro earthquake
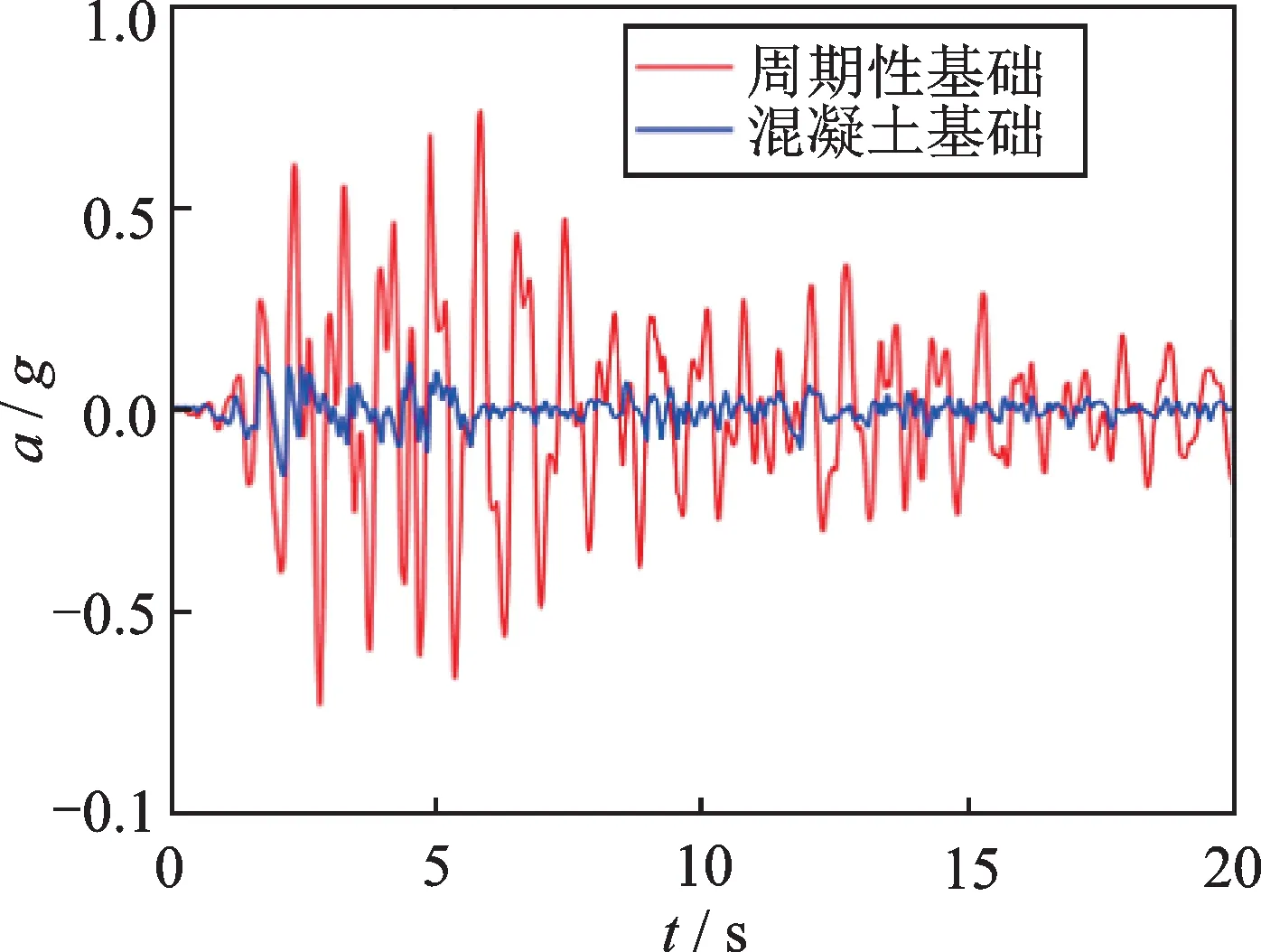
图10 El-Centro地震作用下有限元模型顶部的水平加速度响应Fig.10 Horizontal acceleration response at the top of FEM subject to El-Centro earthquake
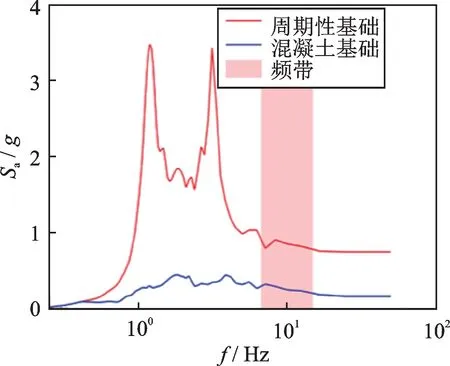
图11 El-Centro 地震作用下有限元模型顶部的水平加速度反应谱Fig.11 Horizontal acceleration response spectrum at the top of FEM subject to El-Centro earthquake
为了解释这一现象,本文分别对FEM-PF 和FEM-FF 进行模态分析。根据模态分析结果,FEM-PF 的前三阶自振频率分别为1.207,1.265 和1.816 Hz。FEM-FF 的前三阶自振频率为25.71,28.16 和45.19 Hz。根据结构动力学中振型叠加法可知,上部结构的动力响应主要是由前几阶振型叠加而成。由于El-Centro 地震波的主频与FEM-PF的前三阶自振频率非常接近,故而产生了明显的共振放大现象;相反,FEM-FF 的前三阶自振频率与El-Centro 地震波的主频相距甚远,上部结构的动力响应也随之变小。因此,当低频地震波处于周期性基础的频率带隙之外时,无法减小上部结构的动力响应,反而会增大结构的动力响应。
3.3.3 Saguenay 地震波
图12表示Saguenay 地震波加速度时程及其傅里叶谱。由图12(b)可知,Saguenay 地震波的一个主频段(10~14.5 Hz)在周期性基础的频率带隙(6.8~15.54 Hz)内,周期性基础有望减小上部结构的加速度响应。图13表示水平Saguenay 地震波激励下上部钢框架顶点P 的水平加速度响应。由图13可知,周期性基础结构顶点的峰值加速度为0.40g,而固定基础结构的顶点加速度峰值为0.87g,周期性基础的加速度峰值减小约54%。图14中的加速度反应谱也验证了地震波主频(12.6 Hz)处于周期性基础的频率带隙内时,周期性基础极大地阻隔地震波的向上传播,从而减小了上部结构的动力响应。
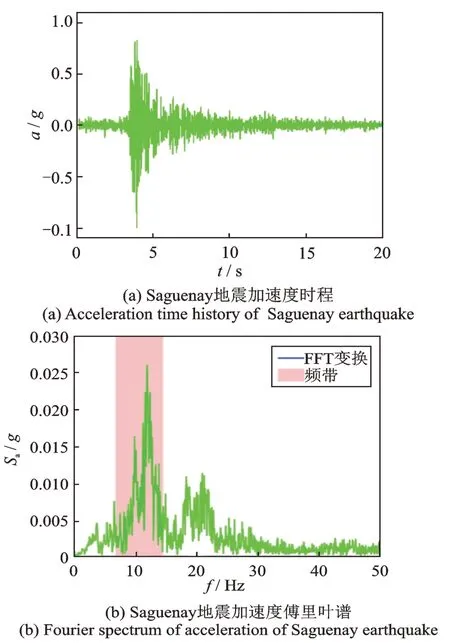
图12 Saguenay 地震加速度时程及其傅里叶谱Fig.12 Acceleration time history and Fourier spectrum of Saguenay earthquake
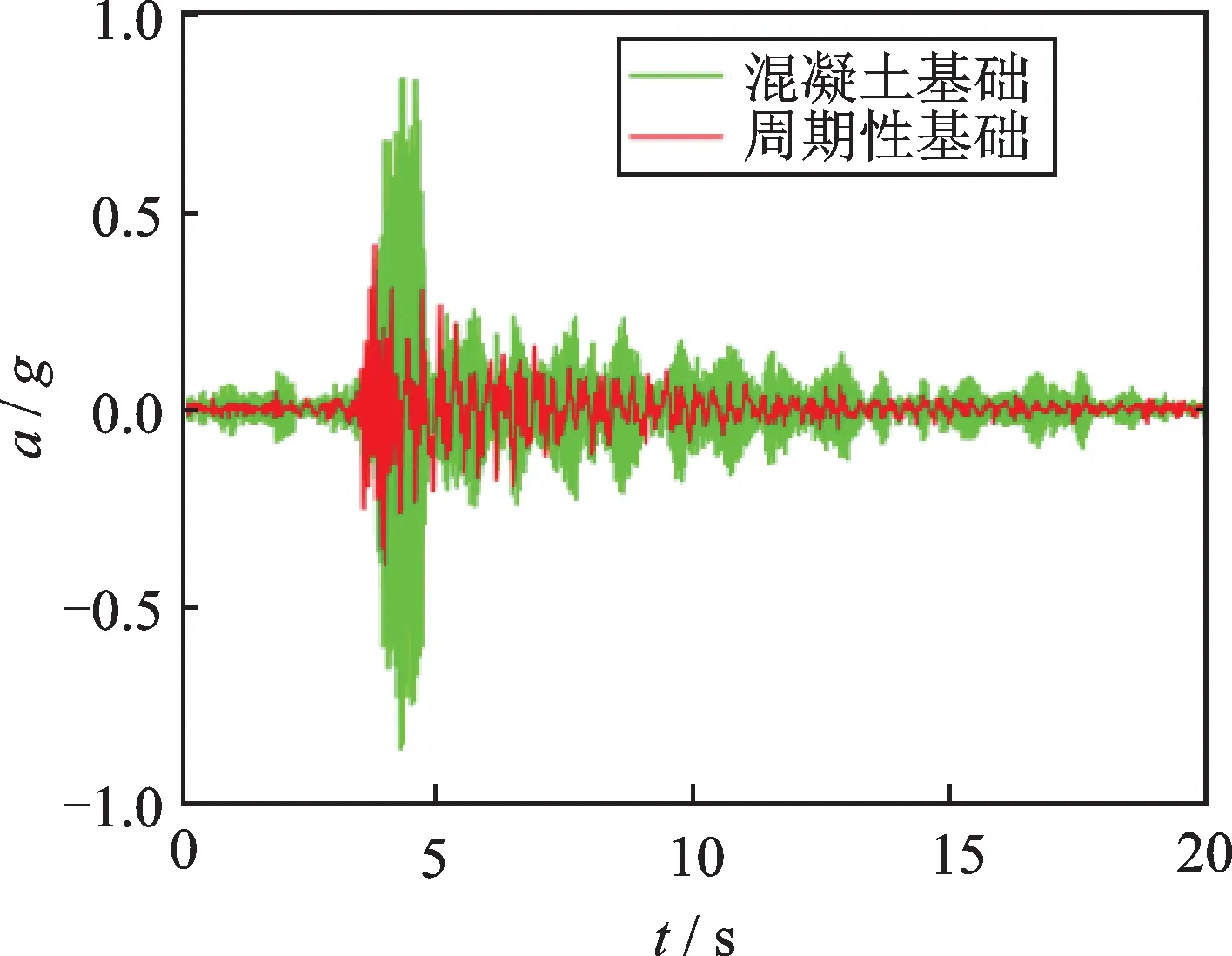
图13 Saguenay 地震作用下有限元模型顶部的水平加速度响应Fig.13 Horizontal acceleration response at the top of FEM subject to Saguenay earthquake

图14 Saguenay 地震作用下有限元模型顶部的水平加速度反应谱Fig.14 Horizontal acceleration response spectrum at the top of FEM subject to Saguenay earthquake
数值分析结果表明,当地震波的主频段处于周期性基础的频率带隙内时,周期性基础可以有效减小上部结构的加速度响应;当低频地震波处于周期性基础的频率带隙外时,由于周期性基础刚度降低,可能导致共振放大现象。
4 周期性基础隔震试验
设计三层钢框架小型振动台试验,验证一维层状周期性基础的隔震效果。
4.1 试件材料属性和几何参数
图15是钢框架的试件布置和试验装置,试件A代表一维层状周期性基础钢框架,试件B 代表固定基础钢框架。周期性基础由两层橡胶和三层混凝土组成。橡胶层与混凝土层之间通过聚氨酯胶粘结,经材料性能试验验证,橡胶与混凝土之间胶水的抗拉力和抗剪力分别大于1000 kN 和6000 kN,确保橡胶和混凝土粘结良好。试件的材料属性和几何参数如表2和3 所示。此外,钢框架的柱、梁和楼板的几何尺寸与第4 节中有限元模型保持一致。

图15 试件布置和试验装置Fig.15 Specimen arrangement and test setup
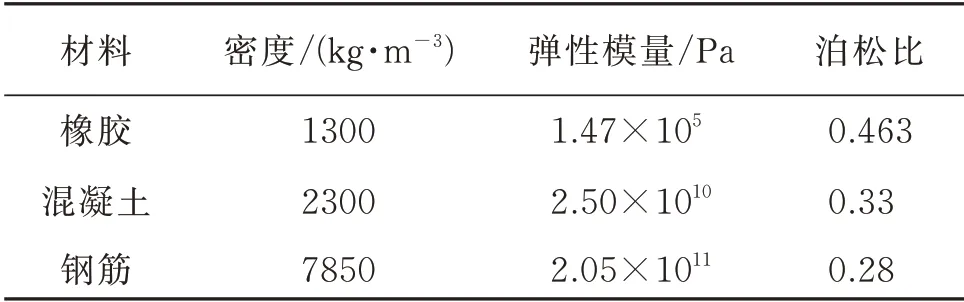
表2 一维层状周期性基础试件的材料属性Tab.2 Material properties of 1D PF test

表3 试件的几何参数Tab.3 Geometric parameters of the specimens
4.2 振动台试验
图16为振动台试验布置图。振动台的平面尺寸为5 m×5 m,可同时提供三个平动自由度和三个转动自由度的动力加载。振动台试验主要包括环境振动测试、地震波测试和单频正弦波测试。用加速度计和位移计装置,分别测量一维层状周期性基础和固定基础上部结构的动力响应。
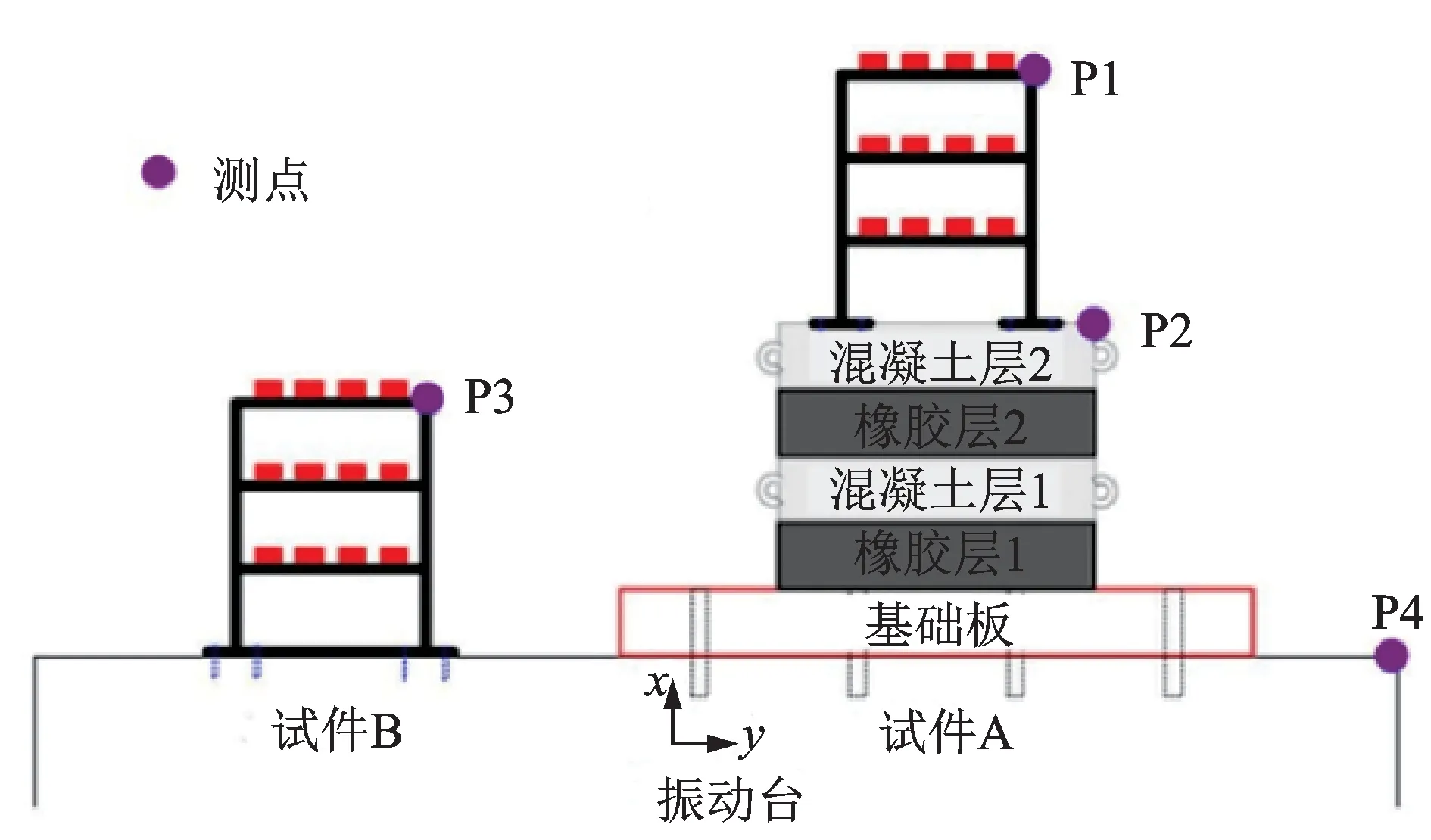
图16 振动台实验布置图Fig.16 Schematic diagram of the shaking table test
4.2.1 环境振动
图17表示的是50 Hz 环境振动激励下周期性基础和固定基础钢框架顶部水平加速度响应。由图可知,周期性基础钢框架顶部(试件A)的水平加速度响应远小于固定基础钢框架顶部(试件B)的动力响应。由于振动台的振动频率处于S 波频率带隙(47.78~62.16 Hz)内,因此周期性基础能有效阻隔弹性波传播。
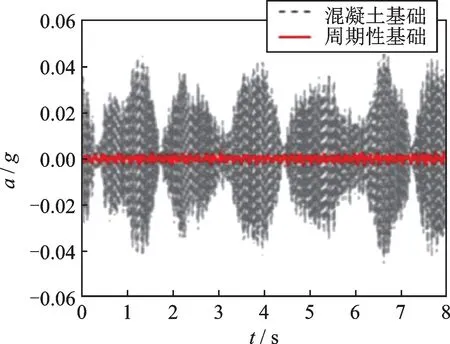
图17 环境振动激励下钢框架顶部水平加速度响应Fig.17 Horizontal acceleration response of the steel frame roof subject to ambient vibration
4.2.2 Oroville 地震波
选择Oroville 地震波进行地震动测试。实验时,振动台仅在一个水平方向输入峰值(PGA)为0.418g的水平地震波,并记录各个测点(见图16)的动力响应。由图18可知,该地震动的主频段(18.1~20 Hz)基本处于周期性基础的第二频率带隙(18.45~31.08 Hz)内。图19表示周期性基础和固定基础上部结构的P1 点和P3 点的水平加速度响应及其反应谱。试验结果表明,试件A(含有周期性基础的钢框架)上部结构峰值加速度相对于试件B(无隔震基础的钢框架)减小了接近49%。
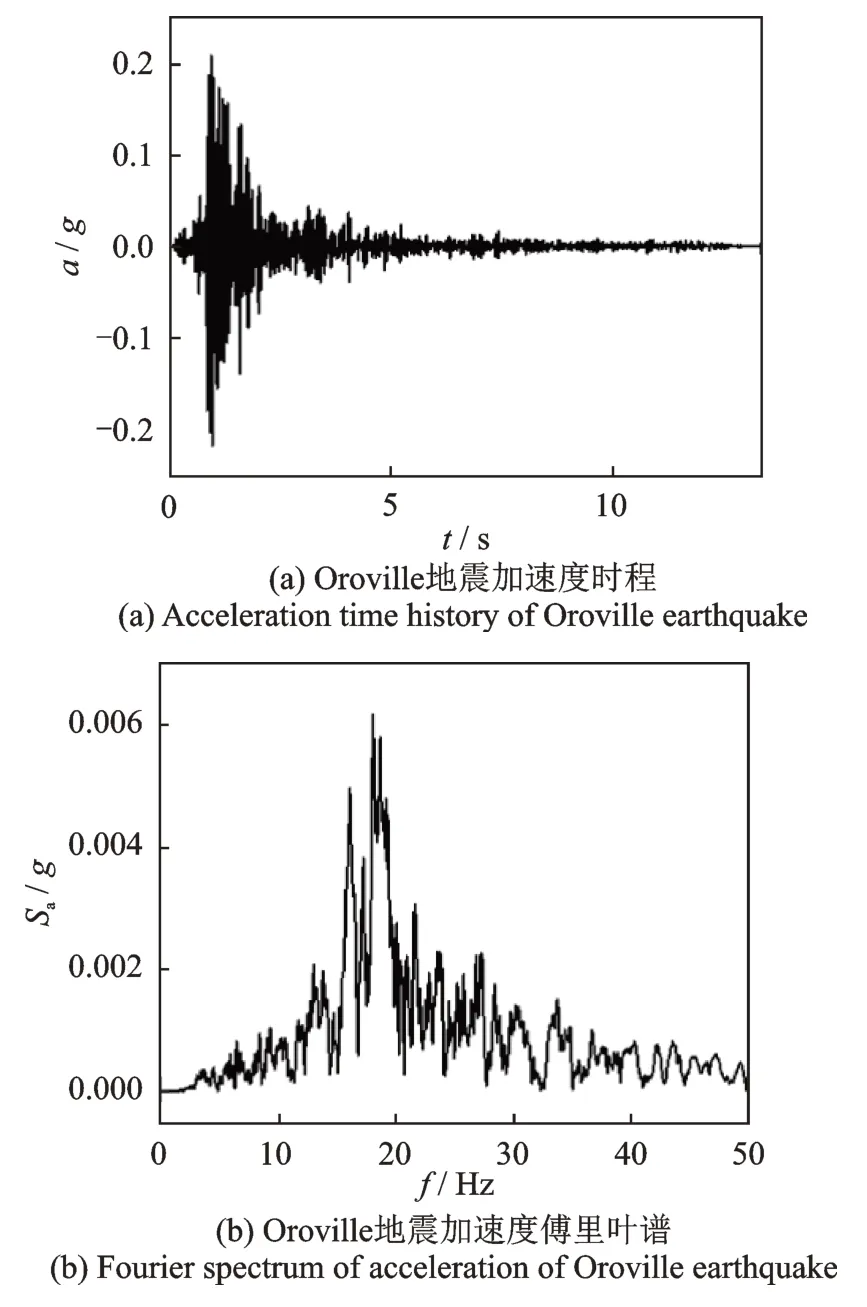
图18 Oroville 地震加速度时程及其傅里叶谱Fig.18 Acceleration time history and response spectrum of the Oroville earthquake
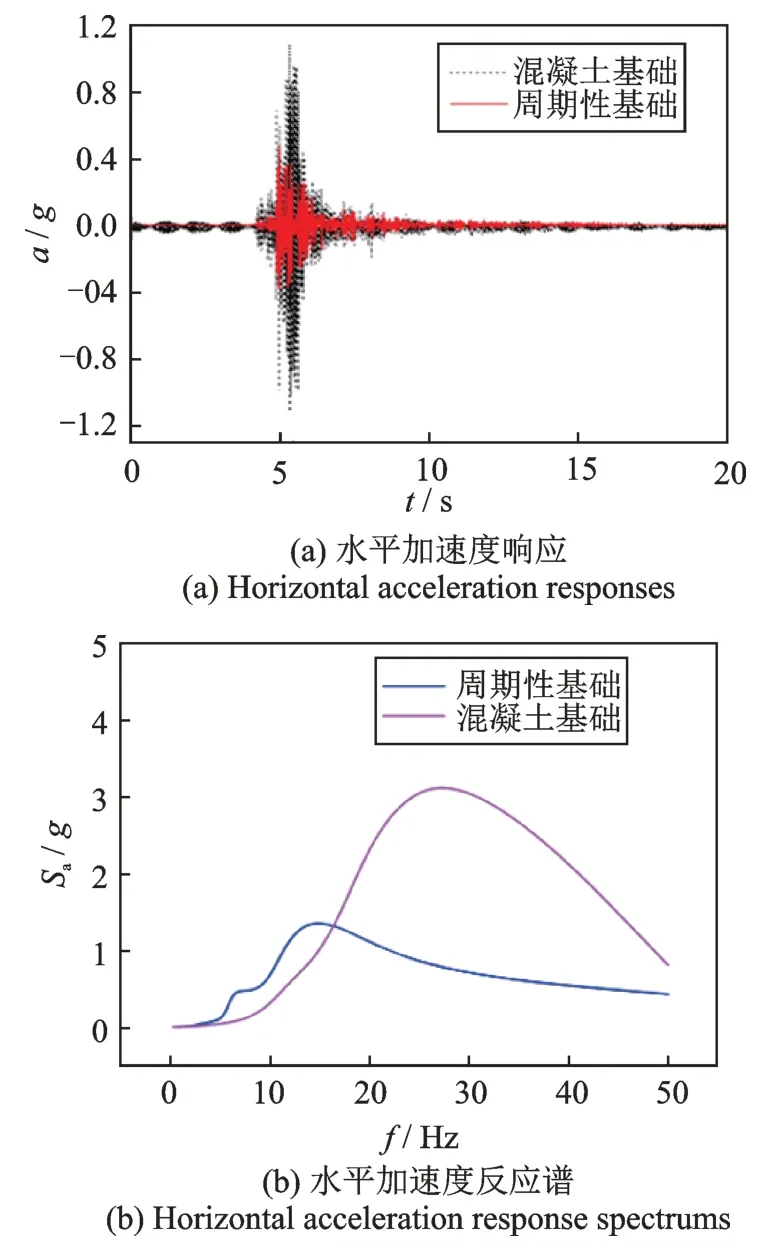
图19 Oroville 地震作用下钢框架顶层水平加速度响应及其反应谱Fig.19 Horizontal acceleration responses and spectrums at the top of steel frame subject to Oroville earthquake
图20是有无周期性基础情况下上部结构顶层的P1 点和P3 点的竖向位移响应。由图可知,试件A(含有周期性基础的钢框架)上部结构竖向位移相对于试件B(固定基础的钢框架)减小了约15.8%。可见,周期性基础不仅可以减小上部结构的加速度响应,同时也可以减小竖向位移。
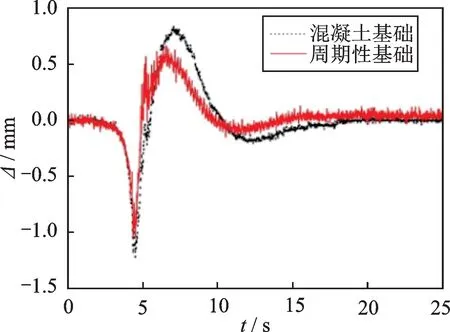
图20 Oroville 作用下钢框架顶层竖向位移响应Fig.20 Vertical displacement response at the top steel frame subject to Oroville earthquake
4.2.3 正弦波
环境振动测试、地震波测试的结果均表明,周期性基础对处于频率带隙内部的输入波具有很好的阻隔效果,极大地衰减了水平方向的动力响应,同时也能减小竖向动力响应。为了全面反映周期性基础的带隙特性,选择处于频率带隙外(f= 6 Hz)的正弦波作为输入波,测试上部结构的动力响应。图21表示两个试件顶部水平方向加速度响应。周期性基础框架顶部峰值加速度为0.53g,固定基础框架顶部峰值加速度为0.46g。因此,正弦波频率处于频率带隙之外时,周期性基础框架结构的动力响应无法减小,反而略有放大,这一现象也与第3 节的数值分析结论相一致。
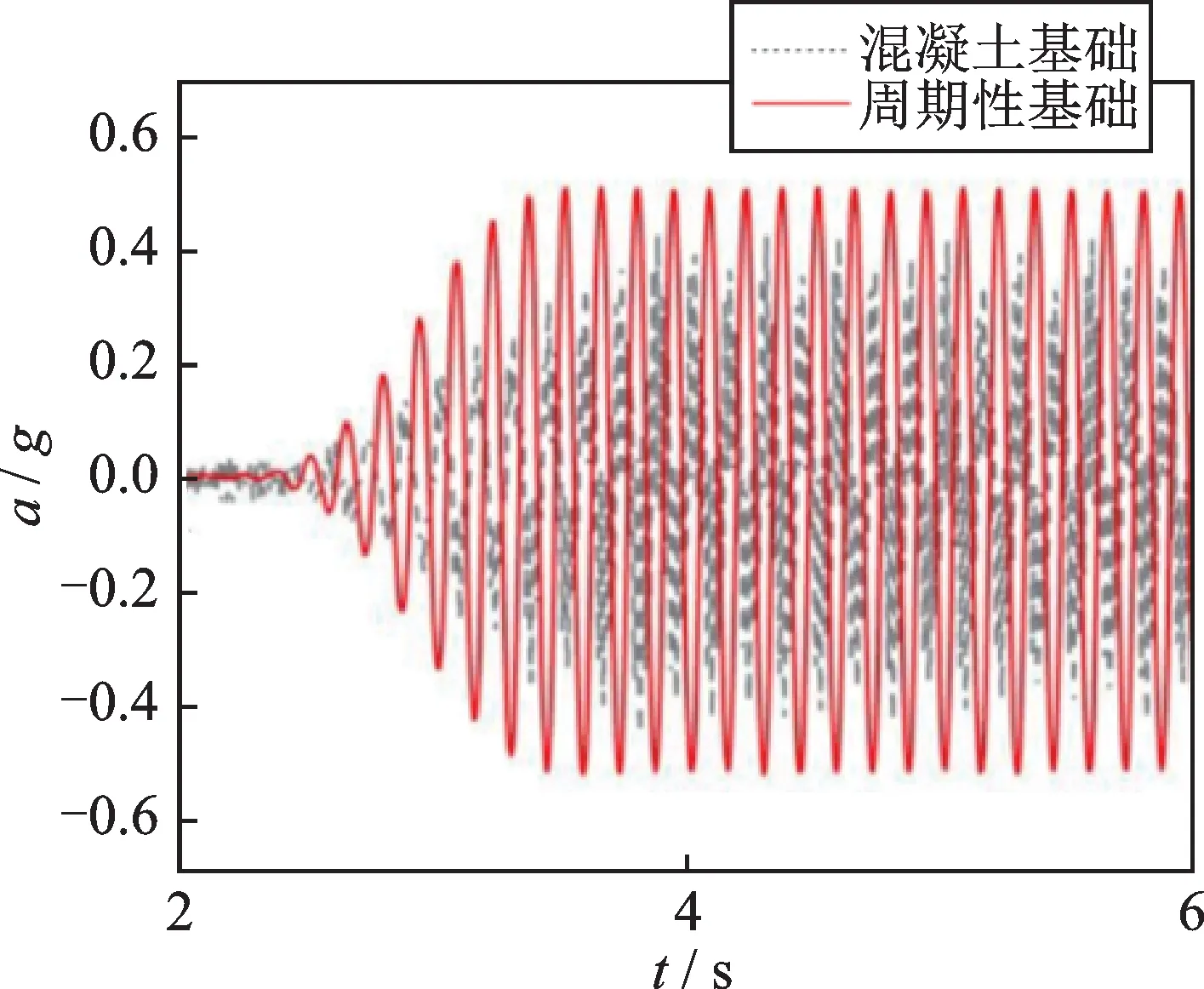
图21 正弦波作用下钢框架顶部水平加速度Fig.21 Horizontal acceleration at the top of steel frame subject to sine wave
5 结 论
本文借鉴固体物理学中声子晶体的概念,选择橡胶和混凝土两种材料构造一维复合周期性基础,并建立频散方程分析其带通特性。通过数值方法,对含有一维周期性基础和普通钢筋混凝土基础的三层钢框架的衰减效果进行研究,并设计小型振动台试验进行验证。主要结论如下:
1)与普通叠层橡胶支座的隔震机理不同,基于固体物理学中的周期理论设计的一维层状周期性基础可产生频率低于50 Hz 的弹性波带隙,基本覆盖地震动的主要频段。
2)振动台试验结果表明,相对于固定基础的上部结构,含周期性基础钢框架的水平峰值加速度降低约49%,竖向位移减小约15.8%,即周期性基础不仅可以减小上部结构的加速度响应,同时也可以减小竖向位移。
3)理论分析、数值模拟和试验均表明,当激励频率处于周期性基础的频率带隙内时,所提出的一维层状周期性基础可有效地阻隔环境振动或地震波的传播,从而减小上部结构的动力响应。
4)尽管关于周期性基础的初步研究表明其具有传统隔震技术无法比拟的优异性能,但是目前的理论研究和数值分析大都局限于线弹性理论,周期性基础的非线性特征、上部结构与基础的相互作用、场地条件等因素对周期性基础动力特性和衰减域的影响仍需要进一步研究。
