高速列车抗蛇行减振器作用机制与频变刚度应用研究

姚 远，程 俊，张名扬，沈龙江

（1.西南交通大学牵引动力国家重点实验室，四川 成都 610031；2.中车株洲电力机车有限公司转向架研发部，湖南 株洲 412001）

引 言

抗蛇行减振器是实现机车车辆安全稳定运行的关键悬挂元件，尤其针对高速列车动力学设计，抗蛇行减振器力学建模、参数优化及其对整车动力学性能影响等问题需要进行系统深入的分析。目前国内典型高速列车采用的转向架悬挂参数和车轮踏面有所不同，所匹配的抗蛇行减振器结构参数也大相径庭［1-2］，因此需要对高速列车抗蛇行减振器作用机制进行理论研究从而对最优减振器参数选配提供指导。关于抗蛇行减振器作用机制，朴明伟等［3-5］针对国内引进欧系高速列车的横向稳定性问题及改进措施进行了深入理论研究，基于抗蛇行减振器频带吸能机制和高频阻抗特性，提出抗蛇行减振器并联组合应用方案以提高车辆横向稳定性裕度和鲁棒性。除机理研究外，国内外针对抗蛇行减振器的性能测试与力学建模［6-11］、参数优化及其对整车动力学性能影响［12-20］等相关研究较为普遍。此外，针对列车不同运行工况对减振器阻尼和刚度参数的不同需求，文献提出采用半主动控制对抗蛇行减振器实现变参数［21-23］。

本文首先分析油液减振器的频变特性和最优能量耗散条件；然后建立两类典型高速列车横向动力学模型并对抗蛇行减振器参数进行多目标优化，基于整车线性稳定性和模态能量分析，总结抗蛇行减振器的作用机制。研究表明，抗蛇行减振器的参数优化需要兼顾高低等效锥度、不同轮轨接触状态下的车辆横向稳定性，而传统固定参数抗蛇行减振器无法较好地实现该目标。为解决该矛盾，提出应用频变刚度抗蛇行减振器的思路，对提高车辆自适应稳定性和改善高速列车在极端轮轨接触状态下车辆横向动力学性能等方面起到积极作用。

1 最优耗散理论

目前铁道车辆上使用的减振器大多为油液减振器，其通过节流孔对油液节流形成阻尼力，从而衰减系统振动。油液减振器在理想情况下，可以用一个阻尼（黏壶）单元来描述力学模型，但实际中需要考虑到油液压缩刚度、阀门变形刚度，以及串联橡胶关节刚度，因此还需引入刚度单元，即黏弹性模型，能同时描述减振器的储能和耗能特性。根据抗蛇行减振器测试数据，采用阻尼和刚度串联的Maxwell 等效参数模型可较好地模拟正常工作条件下减振器的动态特性，相较于考虑流-固-热耦合的三维结构模型，该简化模型在很大程度上节省了计算时间，更加适用于高速列车的动力学仿真计算。减振器阻尼c及串联刚度k组成Maxwell 模型如图1所示，可以描述为：

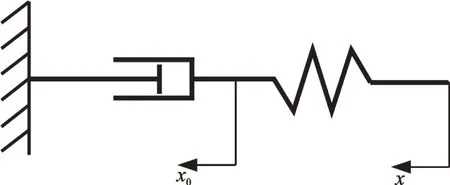
图1 Maxwell 等效参数模型Fig.1 Maxwell equivalent parameters model

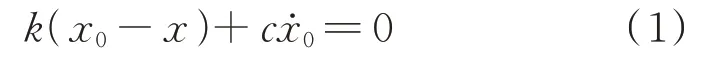
式中x和x0分别为模型端部和中间位置的位移。根据拉普拉斯变换，在复数域内表示为：

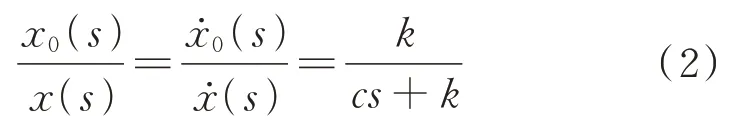
式中s=jω，ω为圆频率，j 为虚数单位。减振器的作用力F可表示为：

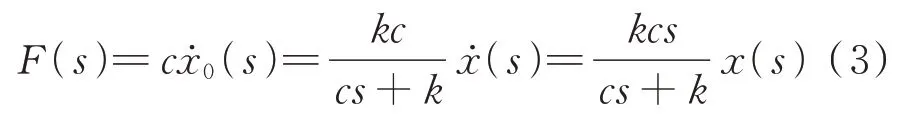
得到减振器两端的等效刚度ke和等效阻尼ce为：

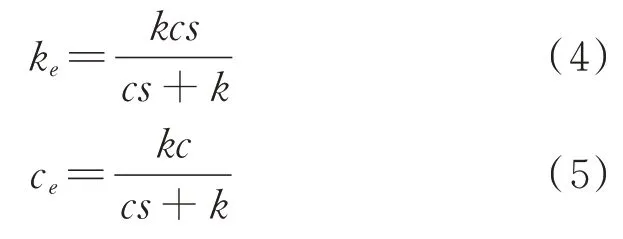
可知等效刚度和等效阻尼都与减振器作用频率有关，称为动态刚度与动态阻尼，其频变特性如图2（a），（b）所示。可见低频工况（如列车蛇行频率2～4 Hz）作用下，减振器的动态刚度ke约为其串联刚度k的一半。随着减振器作用频率增加，减振器等效刚度也增加，而等效阻尼减小。

将s=jω代入式（4），得到ke的复刚度形式：

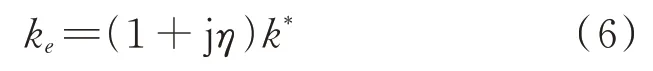
式中 实部k*=，称为储能模量；虚部ηk*为耗能模量，其中η=k/（cω），为损耗因子；ϕ=arctanη为损耗角。储能模量和耗能模量分别表示减振器通过弹性变形储存能量和阻尼将机械能转化为热能的能力，其频变特性如图2（c），（d）所示。随着频率增加，由于等效刚度增强，减振器储能作用增强；耗能作用先增加后减小，即减振器存在最优的能量耗散条件。

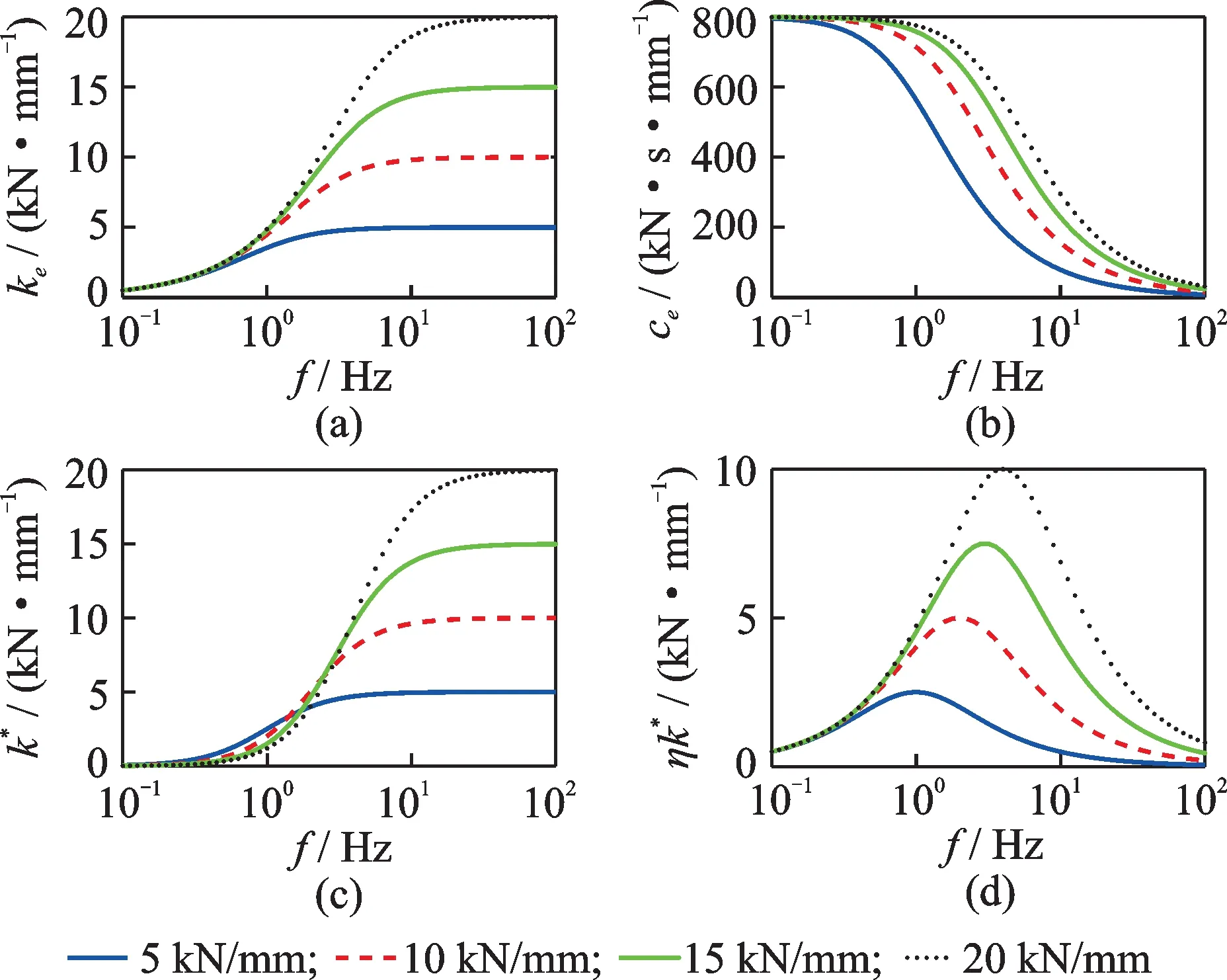
图2 减振器Maxwell 黏弹性模型频变特性Fig.2 Frequency-dependent characteristics of Maxwell viscoelastic model for dampers

当减振器端部受到位移激励x=Asin（ωt）时，设中间位置响应为x0=A0sin（ωt+ϕ），则：

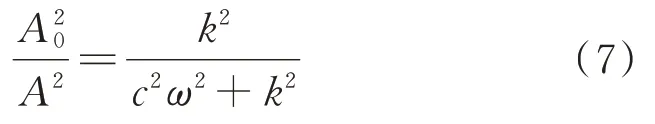
减振器在单位周期内的耗散功W为：

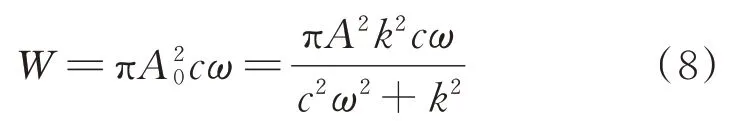
即当减振器作用圆频率ω等于减振器串联刚度k与阻尼c的比值时，减振器的能量耗散功率最大，此时减振器的储能模量等于耗能模量，损耗因子η=1，损耗角ϕ=45°。

2 车辆横向稳定性

2.1 车辆横向动力学模型

为了研究抗蛇行减振器对车辆横向稳定性的影响及其作用机制，建立车辆横向动力学分析简化模型，如图3所示。该模型包括1 个车体，2 个构架，4个轮对，共7 个刚体。车体和构架具有横移、摇头和侧滚自由度；轮对具有横移和摇头自由度。轮对与构架之间为一系悬挂，由横向、纵向和垂向定位刚度组成，模型同时考虑到一系悬挂转臂长度的影响。车体与构架之间设有横向、纵向和垂向二系悬挂刚度和阻尼，以及抗侧滚刚度。抗蛇行减振器和二系横向减振器采用弹簧和阻尼串联而成的Maxwell 等效参数模型，并含单自由度的减振器等效质量刚体。该车辆横向动力学模型共有25 个自由度。本文针对线性模型进行线性稳定性分析，轮轨接触几何采用等效锥度来表示，轮轨切向力采用Kalker 线性理论计算，系统动力学方程如下：

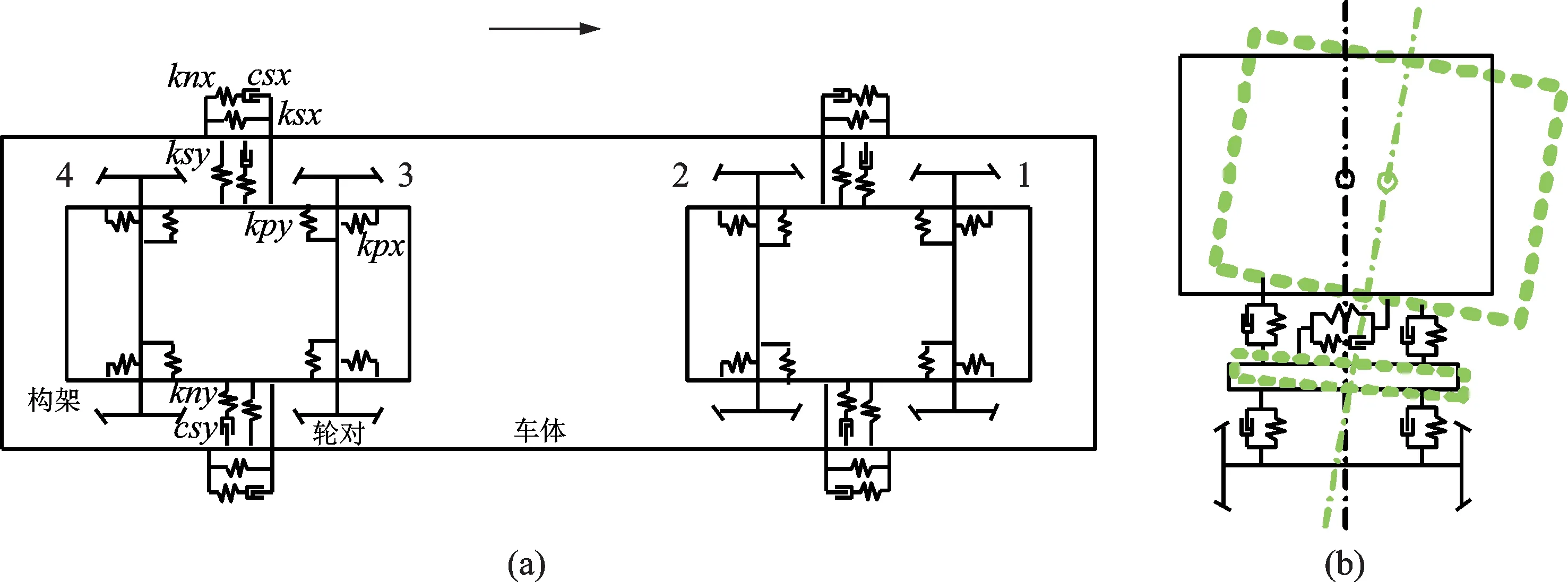
图3 车辆横向动力学简化模型Fig.3 Simplified model of vehicle lateral dynamics

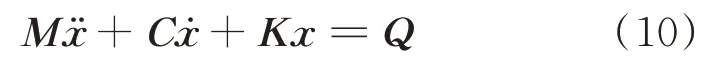
式中x为系统的自由度矢量；矩阵M，C，K和Q分别为系统的质量、阻尼、刚度和外力矩阵。采用复模态计算方法，将上式整理成状态空间形式，计算系统矩阵的特征向量和特征值，得到系统模态振型和模态阻尼。

2.2 线性稳定性

针对目前国内两类典型高速列车进行分析，部分除抗蛇行减振器以外差别较大的悬挂参数如一系纵向刚度kpx、一系横向刚度kpy和二系横向减振器阻尼值csy如表1所示，其他结构参数相同，分别记作Type 1 型和Type 2 型。根据已有研究，该两类列车动力学设计理念不同，Type 1 以较大的抗蛇行减振器阻尼匹配较小的一系纵向刚度，保证较低轮轨接触锥度下的车辆稳定性，而Type 2 采用较小的抗蛇行减振器阻尼，并匹配驱动系统弹性悬挂，其车辆稳定性的等效锥度健壮性较好，随等效锥度在较宽范围变化其横向稳定性裕度变化较小，且车轮型面磨耗较均匀［2］。

表1 两类高速列车悬挂参数Tab.1 Two types of high-speed train suspension parameters

根据公式（10）进行线性特征根分析，求解低频蛇行运动模态对应特征根的实部与特征根的模之比，即蛇行模态阻尼比，定义为系统线性稳定性指标ζ，通常阻尼值为正表明该线性系统为稳定状态。本文选取较小值作为优化方向，故定义ζ为负值时系统为稳定状态。

为了分析抗蛇行减振器的串联刚度kncsx和阻尼csx参数对车辆稳定性的影响，对比两类高速列车模型在不同运行速度和等效锥度时csx和kncsx组合对应的车辆线性稳定性指标，结果如图4所示。其中横轴为变化的kncsx，纵轴为变化的csx，图中的每条曲线代表车辆线性稳定性指标的等高线，颜色越深，代表稳定性指标越小，车辆横向稳定性越好。图中虚线表示不同频率满足公式（9）对应最优耗散条件时，csx和kncsx的匹配关系。图4（a），（b），（c）针对Type 1 型列车，图4（d），（e），（f）针对Type 2 型列车，等效锥度λ分别为0.05，0.17 和0.3 的计算工况，考虑到低锥度工况车辆低速运行时横向稳定性较差，前者计算速度v=200 km/h，后两者v=350 km/h。从图中可以看出，随着等效锥度的增加，两类列车都需要增大串联刚度kncsx以提高车辆蛇行稳定性；对于Type 1 可选用较宽范围内的csx，而对于Type 2，最优csx取值在1000 kN·s/m 左右，且最优csx随等效锥度的增加而增加。另外，图中最优的抗蛇行减振器参数kncsx和csx取值满足公式（9）的最优耗散条件，Type 2 更为明显，最优的kncsx和csx的比值接近车辆蛇行运动圆频率；车辆蛇行运动频率随λ和v的增加而增加，此时抗蛇行减振器的作用频率增加，对应最优kncsx和csx的比值增大。

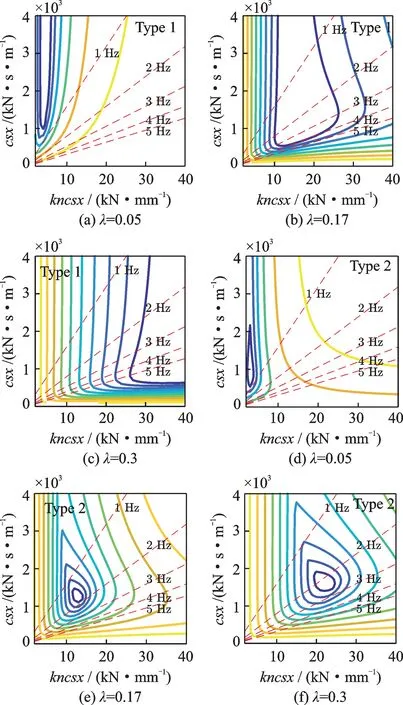
图4 不同抗蛇行减振器阻尼和串联刚度对应的车辆稳定性Fig.4 Vehicle stability corresponding to different damping and stiffness of yaw dampers

总之，两类悬挂参数的高速列车抗蛇行减振器最优刚度都与其轮轨接触等效锥度即对应蛇行频率有关，最优串联刚度随着蛇行频率减小而降低，尤其在低轮轨接触锥度工况，需要较小的串联刚度值，可理解为车体与转向架之间在水平方向需要较小的牵连作用。两类高速列车的抗蛇行减振器作用机制有所不同，在较大数值范围内，抗蛇行减振器阻尼对Type 1 的稳定性影响不明显，而串联刚度的影响显著，即抗蛇行减振器的刚度特性对车辆系统稳定性影响较大；Type 2 除了高频时需要较大串联刚度以外，其稳定性与抗蛇行减振器的最优耗能规律一致，减振器能量耗散越大车辆蛇行运动越稳定，可以基于最优耗散理论实现串联刚度与阻尼的匹配，即串联刚度与阻尼比值等于车辆蛇行运动圆频率。

3 抗蛇行减振器参数多目标优化

3.1 多目标优化设计

机车车辆悬挂参数设计主要是寻找一类折衷的悬挂参数，使其同时兼顾车辆横向稳定性、曲线通过和乘坐平稳性等性能指标。对于横向稳定性而言，当轮轨接触锥度较低时，如新轮、新轨状态，较低的车辆蛇行频率与车体悬挂引起的固有振动频率接近，车辆在低速时容易发生一次蛇行运动（或称车体蛇行），车体出现低频晃动现象，主要影响乘坐平稳性；而车轮踏面或轨距角磨耗后出现较高的轮轨接触锥度使得车辆横向稳定性裕度不足，发生二次蛇行运动（或称转向架蛇行），导致转向架出现高频横向剧烈抖动。为了描述两类不同轮轨接触状态对应的车辆横向稳定性裕度，分别定义低锥度工况车辆稳定性指标ζlow和高锥度工况车辆稳定性指标ζhigh，两种工况计算条件如表2所示。ζ为负值时表示系统在对应的锥度下是稳定状态，且ζ值越小，在该轮轨接触状态下的蛇行运动模态阻尼比越大，其横向稳定性就越好。现有研究发现，ζlow和ζhigh之间在一定程度上存在矛盾，即车辆低锥度稳定性越好，则高锥度稳定性越差，反之亦然［24-26］。高速列车由于运行速度高、线路条件好，传统低速轮轨车辆存在的直线稳定性与曲线通过性能的矛盾并不突出，取而代之的是车辆横向稳定性适用不同轮轨几何接触状态的矛盾。因此，高速列车悬挂参数设计主要是针对不同轮轨接触状态车辆稳定性多目标优化问题。

表2 两个优化目标的工况设置Tab.2 Calculating conditions for two optimization objectives

多目标优化问题通常存在着一个解集，称为Pareto 最优解，其在目标函数空间中的像被称为Pareto 前沿。Pareto 前沿为优化后的目标值，每个点都具有其他点所不具有的优势，可以从中寻找规律，根据设计侧重点不同，可以人为在Pareto 集中选取满足性能要求的优化解。NSGA-Ⅱ算法能够保持类群的多样性，提高计算效率，是目前解决多目标优化问题常用的一类有效算法［27］。本文选用带有精英策略的快速非支配排序遗传算法NSGA-Ⅱ进行多目标优化设计。

将抗蛇行减振器阻尼csx和串联刚度kncsx作为优化对象，两者的参数取值范围分别为100～4000 kN·s/m 和5～20 kN/mm。以车辆低锥度稳定性指标ζlow和高锥度稳定性指标ζhigh为优化目标。该多目标优化问题可以描述为：

3.2 多目标优化结果

图5（a）为得到的Pareto 优化目标前沿，图中的横轴和纵轴分别为车辆的低锥度稳定性指标ζlow和高锥度稳定性指标ζhigh，ζ值越小，对应的稳定性越好。图中清晰地体现了目标ζlow和ζhigh的矛盾关系，即车辆的低锥度稳定性越好，其高锥度稳定性就越差。在给定的抗蛇行减振器csx和kncsx参数取值范围内，Type 1 型列车可实现的最小ζlow和ζhigh分别为−0.3 和−0.3，Type 2 型列车由于模型中未考虑到电机弹性悬挂的影响，仅考虑到抗蛇行减振器参数优化在系统稳定范围内（ζ<0）可实现的最小ζlow和ζhigh仅为−0.1 和−0.1，Type 1 的可实现低锥度稳定性裕度和高锥度稳定性裕度均大于Type 2。

为进一步探究抗蛇行减振器具体参数对车辆横向稳定性的影响，依次假定Maxwell 模型中的刚度值和阻尼值为无穷大（inf）。当刚度无穷大时，抗蛇行减振器可以被当作是一个纯阻尼力元；反之，当阻尼无穷大时，则可当作纯刚度力元。结果如图5（b），（c）所示。对于Type 1，抗蛇行减振器纯阻尼和纯刚度条件下都可实现较好的ζhigh，而纯阻尼条件下ζlow较差；相反纯刚度条件下可实现较好的ζlow。对于Type 2，抗蛇行减振器纯阻尼条件下可实现的ζlow和ζhigh都较差；纯刚度条件下可实现的ζhigh较差，但可实现ζlow与减振器黏弹性模型对应结果相当。由此可见，抗蛇行减振器不仅阻尼起到蛇行能量耗散作用，其小串联刚度值对应的减振器弹性，尤其是低锥度轮轨接触状态对车辆横向稳定性影响更显著。

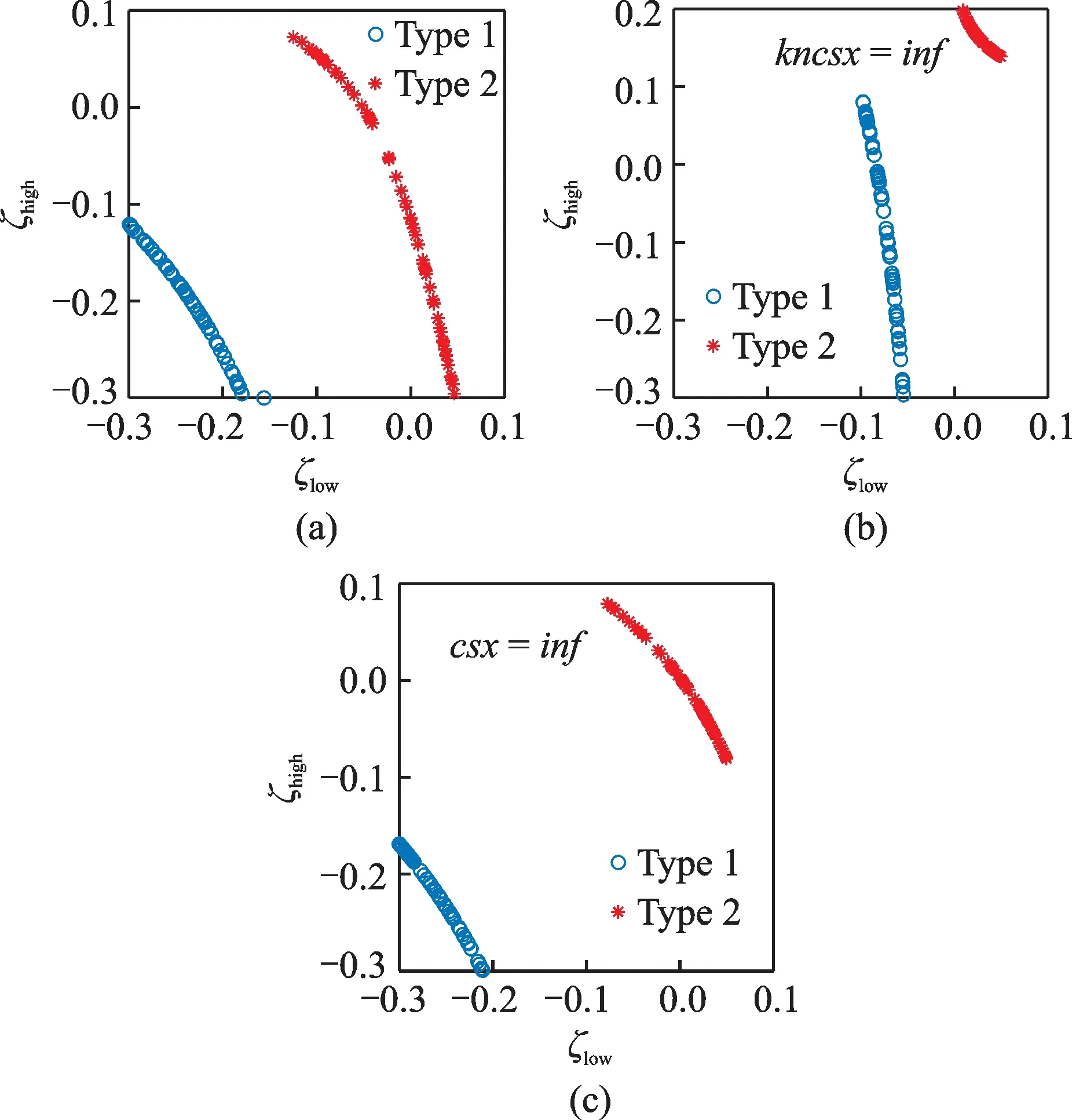
图5 两类列车对应的最优线性稳定性指标Fig.5 Optimal linear stability indexes of two types of vehicle

图6（a），（b）是对两类列车抗蛇行减振器参数进行多目标优化后得到的Pareto 集，反映优化后参数与目标之间的关系。各子图的横轴为低锥度稳定性指标ζlow，纵轴分别为抗蛇行减振器阻尼csx和串联刚度kncsx。对于Type 1，csx最优解分布较为集中，为给定优化参数范围的上限（与图4中较大范围的csx优化值不同，说明了多目标优化方法对寻找次优化解的局限），为保证Type 1 良好的稳定性，需要较大的csx；对于Type 2，csx最优解取值较小，分布在600～1000 kN·s/m。计算得到最优解与两类列车实际抗蛇行减振器阻尼值相吻合，说明了简化动力学模型与分析方法的合理性。更为重要的是，对应不同轮轨接触锥度，Type 1 和Type 2 抗蛇行减振器串联刚度kncsx对车辆稳定性的影响规律一致，即kncsx随ζlow值的减小而减小。由此可知，为提高车辆低锥度稳定性，应减小kncsx取值，而增大kncsx则有利于高锥度稳定性。图6（c），（d）分别为抗蛇行减振器采用纯阻尼和纯刚度模型对应的最优csx和kncsx，减小csx和kncsx有利于列车低锥度横向稳定性。

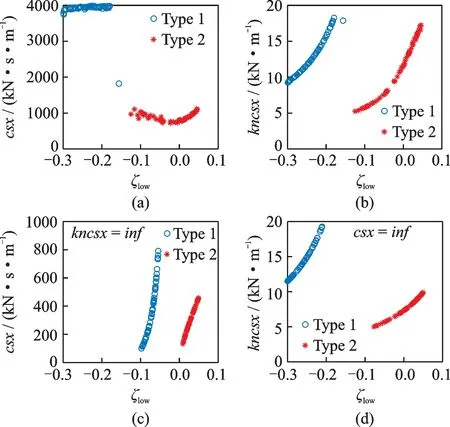
图6 最优抗蛇行减振器参数Fig.6 Optimal parameters for yaw damper

3.3 最优悬挂参数影响因素分析

高速列车抗蛇行减振器最优阻尼参数选取主要受二系横向减振器阻尼值的影响，与一系定位刚度关联不大［25］。现选取二系横向减振器阻尼csy，分析其取值对抗蛇行减振器参数优化结果的影响。图7为不同csy计算得到的Pareto 集，csy取值范围为10～50 kN·s/m。图7（a），（c）呈阶梯状分布，随着csy取值的增大，对应的抗蛇行减振器阻尼csx最优解会由较小值突变到较大值。即csx最优解取决于csy，当csy数值较小时，csx最优解取值较小，一般不超过1000 kN·s/m；csy数值较大时，csx最优解集中在优化区域上限4000 kN·s/m 附近。因此，为保证车辆良好的蛇行运动稳定性，在进行悬挂参数优化设计时，要注意抗蛇行减振器阻尼和二系横向减振器阻尼之间的匹配，即二者数值同时取较小或者较大值。csy对抗蛇行减振器刚度kncsx优化解的影响不大，在csy较小时可实现的低锥度稳定性裕度小于csy取值较大时能达到的低锥度稳定性裕度，由此得出表1中两类高速列车悬挂参数匹配的主要差别。图7中反映的kncsx对车辆稳定性的影响与前文一致，增大kncsx，车辆低锥度稳定性随之降低，高锥度稳定性提升。

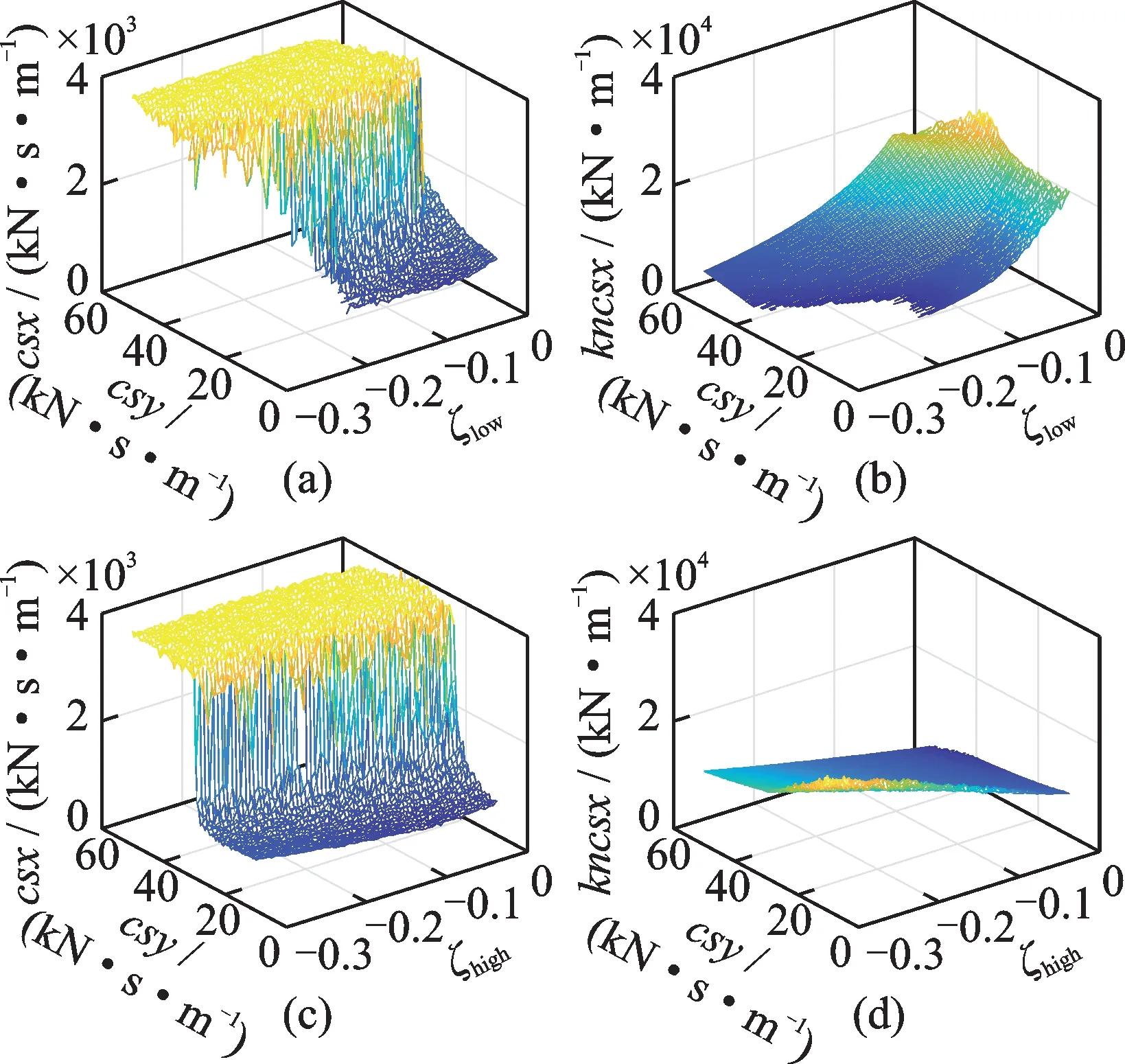
图7 不同csy 对应的csx 和kncsx 最优解Fig.7 Optimal solutions of csx and kncsx corresponding to different csy

4 系统根轨迹与模态能量分析

为了深入研究高速列车抗蛇行减振器作用机制，对两类列车的车辆横向动力学线性模型根轨迹与蛇行模态能量进行分析。Type 1 和Type 2 在不同轮轨接触等效锥度λ和抗蛇行减振器刚度kncsx对应的车辆线性系统根轨迹曲线如图8和9 所示，两类列车csx采用图6（a）中的优化结果。图中每个‘+’号代表某个振型在某个速度下的振动频率和模态阻尼比，较大的‘+’号表示较大的运行速度，图中速度为20～800 km/h。图中横轴表示模态阻尼比，为系统矩阵特征值的实部与特征值的模数之比，-ζ为负值表示稳定状态，值越小，车辆横向蛇行运动越稳定。当> 0 时，车辆系统发生蛇行失稳。纵轴表示模态频率f，对应特征值虚部。文中重点分析频率小于10 Hz 范围内振动模态的根轨迹。

图8 Type 1 随着运行速度变化的根轨迹曲线Fig.8 Root locus curves of Type 1 varying with operating speed

对于Type 1，其车辆横向稳定性由两条首尾相接的类似“S”形的蛇行运动根轨迹曲线决定，其低锥度稳定性较好。对于λ为0.05 的低锥度工况，频率约为1 Hz 的低频蛇行模态（一次蛇行）的阻尼比靠近0 点，决定了车辆蛇行稳定性，减小kncsx有利于提高车辆蛇行稳定性，如图8（b）所示；对于λ为0.17 和0.3 的高锥度工况，高速工况频率大于5 Hz的蛇行模态（二次蛇行）稳定性较差，增大kncsx有利于提高车辆蛇行稳定性，如图8（c），（d）所示。根轨迹分析得出该类列车具有高低频率的两条蛇行模态根轨迹曲线，低轮轨接触锥度时车辆低频蛇行模态（一次蛇行）决定了系统稳定性，高轮轨接触锥度时高频蛇行模态（二次蛇行）决定了系统稳定性。随着速度或轮轨接触等效锥度增加，车辆临界失稳模态由低频一次蛇行跃迁为高频的二次蛇行，即对应于车辆非线性动力学范畴的亚临界分岔特性。

对于Type 2，其车辆横向稳定性由单条类似“C”形的蛇行运动根轨迹曲线决定，该车蛇行模态阻尼比随着速度变化其变化范围较Type 1 小，即具有较好的等效锥度健壮性。同样，在较低速和较高速工况，其车辆低频一次蛇行和高频二次蛇行稳定性较差，位于中间速度的蛇行运动稳定性较好。如图9所示，与Type 1 规律一致，减小kncsx有利于提高车辆低频一次蛇行稳定性，而增大kncsx有利于提高车辆高频二次蛇行稳定性。与Type 1 不同的是，该类列车横向稳定性由单条根轨迹曲线的蛇行模态决定，即随着速度或轮轨接触等效锥度增加，车辆临界失稳模态由低频一次蛇行逐步演变为高频的二次蛇行，不会出现蛇行频率跃迁情况，对应车辆非线性动力学范畴的超临界分岔特性。

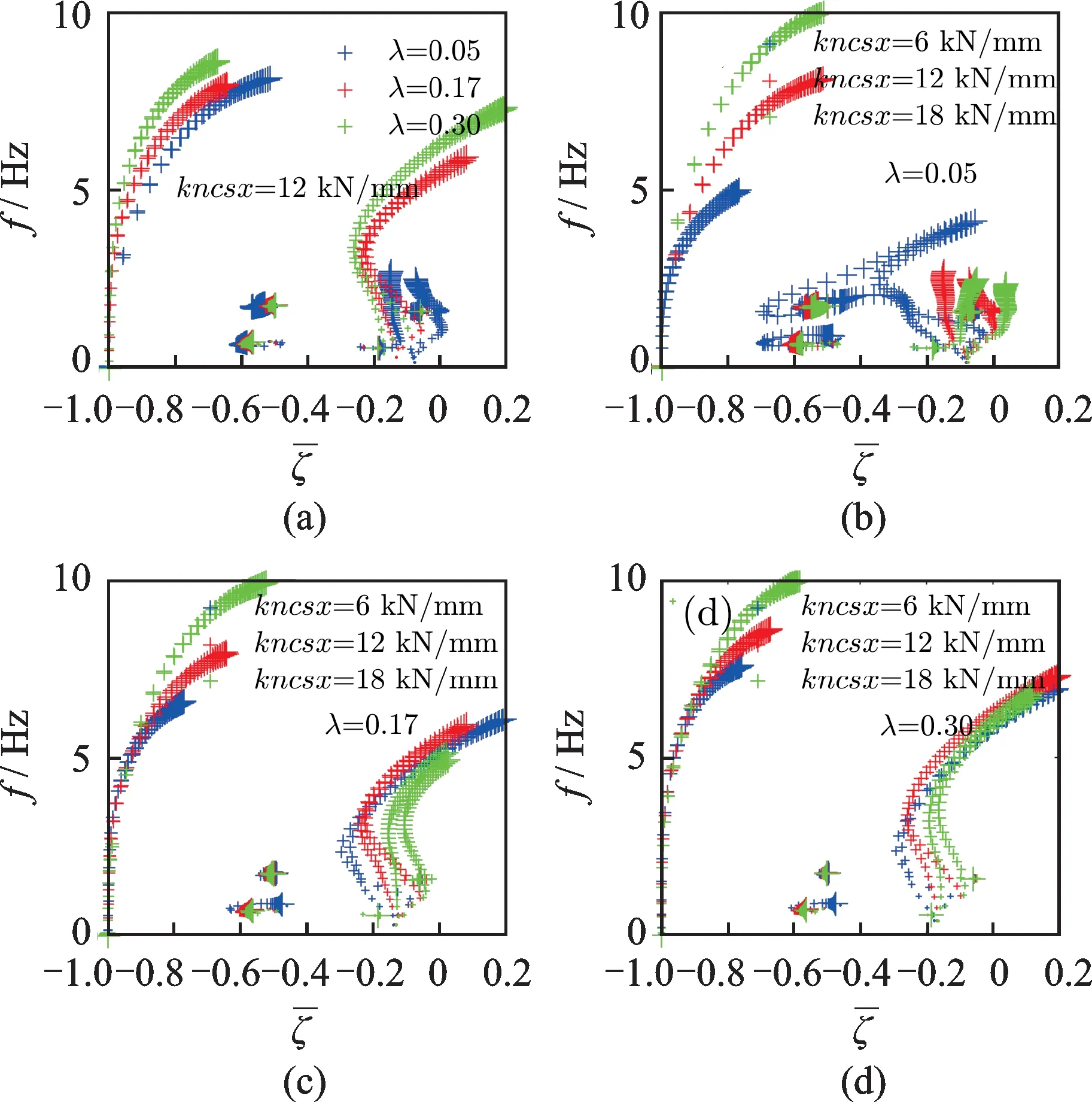
图9 Type 2 随着运行速度变化的根轨迹曲线Fig.9 Root locus curves of Type 2 varying with operating speed

采用该两类匹配模式的悬挂参数对应车辆线性系统根轨迹曲线具有较大差别。根据模态能量分析，两类列车在不同运行速度时对应的车体和转向架蛇行能量占比如图10所示。图中暗红色表示车体蛇行能量占整车的100%，反之，蓝色部分表示转向架蛇行能量占比较高。可见，两类列车低频一次蛇行车体蛇行运动能量较大，而高频二次蛇行以转向架蛇行运动为主。列车实际运行中，当横向稳定性较差或发生失稳时，前者以低频车体蛇行造成的“晃车”现象为主；后者以高频转向架蛇行造成的“抖车”现象为主。根据不同频段车辆蛇行能量占比及抗蛇行减振器参数优化规律，可以归纳高速列车抗蛇行减振器的作用机制：轮轨接触等效锥度较低时，车辆蛇行运动为以车体蛇行能量为主的低频一次蛇行，较小的抗蛇行减振器刚度减小了车体与转向架之间的牵连作用，有利于转向架稳定运行；而当等效锥度较高时，以转向架蛇行能量为主，较大抗蛇行减振器刚度有利于相对静止的车体抑制转向架蛇行运动，提高列车运行横向稳定性。转向架蛇行频率与能量随轮轨接触等效锥度增大而增大，基于抗蛇行减振器的最优能量耗散条件，相应的抗蛇行减振器串联刚度需增加。

图10 车体与转向架模态能量占比Fig.10 Proportion of modal energy between carbody and bogie

5 抗蛇行减振器频变刚度及影响

传统固定刚度及阻尼参数油液抗蛇行减振器，其随作用频率增加的动态刚度幅度增加有限，不易兼顾较大轮轨接触等效锥度范围内车辆横向稳定性的要求，极端轮轨接触状态车辆横向稳定性较差。频变刚度抗蛇行减振器通过串联频变刚度弹性元件，在一定频率范围内可实现减振器较大幅度的动刚度。低锥度工况条件下较小的抗蛇行减振器串联刚度满足车辆低锥度稳定性要求；同时，高锥度工况条件下较大的减振器刚度有利于提高车辆高锥度稳定性。因而频变刚度抗蛇行减振器可自动调整参数，使高速列车在不同轮轨接触状态下具有较强的横向稳定性。

针对Type 1 和Type 2 型高速列车，优化两种频变刚度曲线如图11所示，减振器刚度随着频率增加而增加，Type 1 相对于Type 2，其动刚度幅值需求较大。液压橡胶关节（衬套）内设有液体腔和阻尼通道，如图12所示，通过液体阻尼特性实现其低频低刚度和高频高刚度的动态特性，其频变刚度特性正适合高速列车抗蛇行减振器于不同作用频率下提高车辆横向稳定性的要求。通过改变液体腔的大小、流道的位置、数量和形状等方式实现不同频变刚度特性。液压橡胶关节（衬套）在汽车发动机和底盘控制臂等领域有着成熟的应用，将其通过适应性改进后，应用于高速列车抗蛇行减振器两端橡胶关节具有结构可行和技术可靠的优点。将液压橡胶关节替换原高速列车采用的固定参数抗蛇行减振器橡胶关节，以满足不同轮轨接触状态下车辆稳定性对抗蛇行减振器频变刚度特性的要求。除此以外，利用减振器内部特殊阀结构，可以实现减振器的频变刚度和阻尼特性，如KONI 公司的FSS 和FSD 系列减振器。

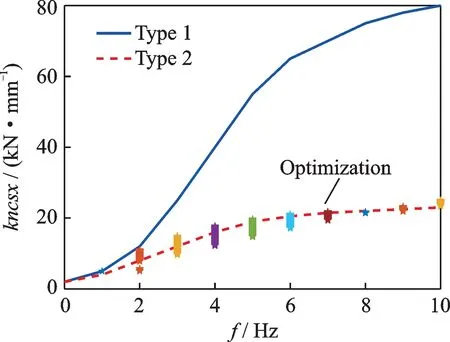
图11 抗蛇行减振器频变串联刚度Fig.11 Frequency-dependent series stiffness of yaw damper

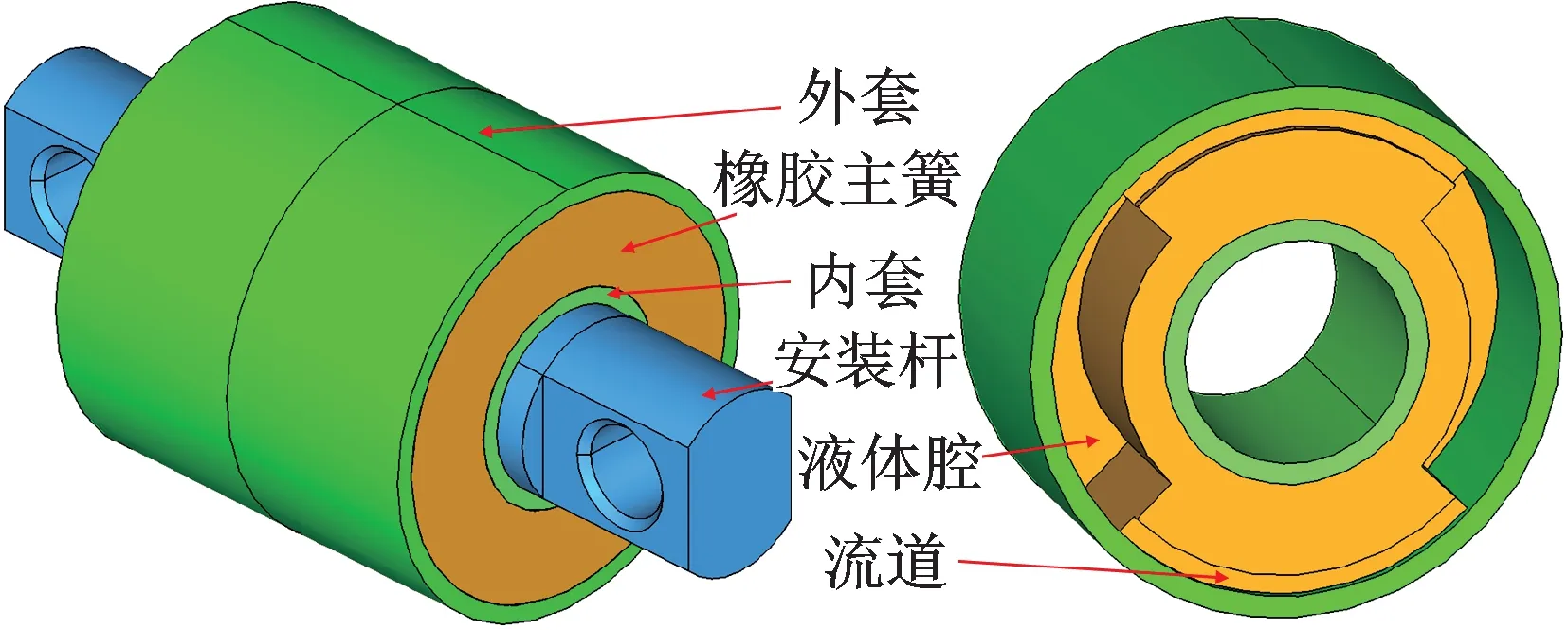
图12 液压橡胶关节结构示意图Fig.12 The structure of hydraulic rubber joint

保持车辆其他悬挂参数不变，抗蛇行减振器分别采用图11中频变刚度曲线（SDF）和定刚度（Const）参数对两类列车的横向稳定性进行分析。对于频变刚度模型进行线性系统分析，可沿着频变刚度曲线通过迭代方法搜索到稳定的系统振动频率与串联刚度值。绘制随轮轨接触等效锥度变化的车辆系统根轨迹曲线，如图13所示。图中较大符号圆表示较大等效锥度λ，其计算范围为0.02～0.6。重点分析频率低于10 Hz 车辆蛇行模态根轨迹曲线，如图13（c），（d）所示。

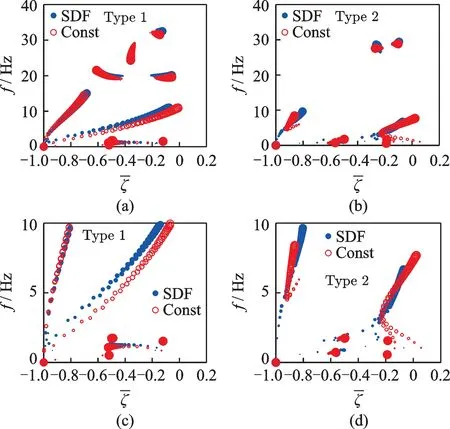
图13 车辆等效锥度变化的根轨迹曲线Fig.13 Root locus curves of vehicle varying with equivalent conicity

对比可知，采用具有频变刚度特性的抗蛇行减振器可以明显改善极端轮轨接触锥度状态下车辆的横向稳定性，尤其对于Type 2 型列车，其车辆低锥度横向稳定性显著增强，减小了列车低频晃车的风险；同样，车辆高轮轨接触锥度时横向稳定性也有改善。因此，频变刚度抗蛇行减振器对于高速列车具有实际工程意义，能够自动调整参数，对改善不同轮轨接触状态高速列车稳定性具有显著的效果。

6 结 论

（1）考虑实际结构及其他影响因素，抗蛇行减振器具有阻尼和刚度双重特性，采用阻尼和刚度串联的Maxwell 黏弹性模型可以模拟正常工作条件下减振器的频变特性；减振器存在最优能量耗散条件，即当减振器作用圆频率等于串联刚度与阻尼的比值时，减振器的能量耗散功率最大。

（2）针对国内运行的两类典型高速列车进行抗蛇行减振器参数优化和车辆横向稳定性分析，对于Type 1，抗蛇行减振器阻尼在较大范围内对车辆稳定性影响不明显，而Type 2 阻尼参数的影响较大，减振器能量耗散特性对车辆稳定性影响明显，基于最优耗散理论实现抗蛇行减振器串联刚度与阻尼的匹配，即刚度与阻尼比值等于车辆蛇行运动圆频率。

（3）随着车辆蛇行运动频率增加，两类高速列车优化的减振器刚度值需增加。轮轨接触等效锥度较低时，车体蛇行能量较大，较小的抗蛇行减振器等效刚度减小了车体与转向架之间的牵连作用，有利于转向架稳定运行；而当等效锥度较高时，以高频转向架的蛇行能量为主，较大抗蛇行减振器等效刚度有利于车体对转向架蛇行运动的抑制。

（4）提出串联液压橡胶关节增强抗蛇行减振器频变刚度特性的结构方案，针对高速列车优化频变刚度曲线，对整车稳定性进行分析。结果表明，应用频变刚度抗蛇行减振器可实现列车在不同车轮踏面磨耗阶段和轮轨接触状态的自适应稳定性，改善极端轮轨接触状态下车辆的横向动力学性能，并可降低对车轮踏面和钢轨廓形维护的要求，减小高速列车运维成本。