含分布式单向单颗粒阻尼器的减震结构体系有限元模拟及性能分析

王宝顺，何浩祥，闫维明，兰炳稷

（北京工业大学工程抗震与结构诊治北京市重点试验室，北京 100124）

1 概 述

颗粒阻尼减振是将颗粒材料按某一填充率放入结构内部或特定的空腔容器中，当受控结构振动时颗粒与颗粒及腔体之间将不断地发生碰撞和摩擦，通过动量交换及消耗系统的振动能量来减轻结构振动［1-3］。由于传统颗粒的直径过大，若将如图1（a）所示的单颗粒阻尼器直接应用于土木工程结构［4］，难以满足工程需求。尽管如图1（b）所示的多颗粒阻尼器满足工程需求［5］，但是在振动工程中颗粒的堆积效应会限制颗粒运动，导致颗粒与受控结构之间动量交换效率及减振效果偏低。有鉴于此，闫维明等［6］提出了如图1（c）所示的并联式单向单颗粒阻尼器（Parallel Single-dimensional Single Particle Damper，PSSPD），能够分布式布置在结构中，具有机理明确、减振频带宽、减振效率更高且适合应用于建筑结构减振等优点。

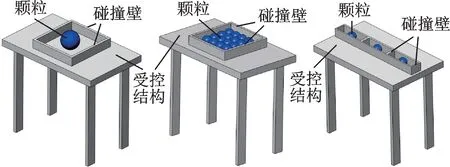
图1 颗粒阻尼器示意图Fig.1 Schematic diagram of particle damper

近年来，有关颗粒阻尼器的研究主要针对阻尼器的减振机理、减振性能与减震效果，减振对象基本是单自由度结构。例如在理论分析方面，Masri等［7-8］推导了附加单颗粒阻尼器的受控结构在周期激励下稳态振动时的解析解。王宝顺等［9-10］在Masri所建力学模型的基础上，考虑了颗粒与受控结构之间摩擦的影响，并对其性能进行对比研究，结果表明考虑摩擦效应之后其减振效果有所降低。在试验研究方面，闫维明等［11］做了一系列多颗粒阻尼器减振机理与性能的试验研究，明晰了其减振性能以及各因素对性能的影响规律。鉴于分析多颗粒阻尼器中颗粒之间相互作用的复杂性，因而学者研究出了一些数值模拟方法，如多相流体理论［12］及离散单元法［13］等。Saeki［14］以在水平激励下的单自由度结构为研究对象，采用离散单元法研究了相关参数对多颗粒阻尼器性能的影响，并进行了试验验证。在颗粒阻尼器有限元模拟方面，程杨［15］通过使用离散元软件EDEM 模拟分析了颗粒阻尼器自身参数对阻尼比的影响并进行了优化。黄韵文［16］通过ANSYS LSDYNA 实现对单层颗粒阻尼器性能的模拟，但计算效率低，且当颗粒个数较多时，计算结果不收敛，该方法已无法胜任；而颗粒阻尼器对多自由度结构进行减振控制时，将有限元（FEM）与离散单元法（DEM）相结合应用于多自由度结构的减振控制设计是一种行之有效的途径。例如Xia 等［17］基于FEM和DEM 耦合算法，利用颗粒阻尼对车辆的旋转制动鼓控制其噪声和振动，实现了颗粒阻尼器的设计与计算。夏兆旺等［18］针对带颗粒阻尼器的旋转平板叶片结构提出基于FEM 和DEM 的耦合仿真算法，证明了所提出的耦合仿真算法在很宽的频带范围内都是可行的。Rong 等［19］也采用FEM 和DEM 的耦合算法研究调谐型颗粒阻尼器对输电塔的减震效果，其中输电塔采用ABAQUS 软件进行有限元分析，基于Python 语言模拟阻尼器的性能。但是FEM 与DEM 耦合对使用者的理论水平要求较高，并且建模难度大、建模环境复杂，很难获得宏观规律，目前只能适用于简单结构，因此不适用于颗粒阻尼器在实际土木工程应用中的推广。

目前关于附加颗粒阻尼器的多层结构的减振机理和性能研究较少，也不够深入。Li等［20］将一种缓冲型碰撞阻尼器设置于三自由度结构体系中，通过自由振动和强迫振动试验评价了该型阻尼器的碰撞和阻尼特性。鲁正等［21］将颗粒阻尼器设置于多自由度结构体系中进行结构动力响应的振动台试验研究，结果表明颗粒阻尼器对多自由度结构的第一振型控制效果较好，但是对高阶振型的控制作用无法保证。该现象主要是由于将颗粒阻尼器集中布置在结构顶层造成的，并没有充分发挥颗粒阻尼器分布式布置的优势。关于颗粒阻尼器布置方案的研究，王瑾等［22］通过对附加颗粒阻尼器的多层钢筋混凝土框架结构的振动台试验研究阻尼器布置位置对其减震效果的影响，结果表明该阻尼器宜布置于结构位移响应较大的位置，然而该结论是基于试验和工程经验得到的，缺乏坚实的理论依据，尚需进一步验证。

纵观现有颗粒阻尼器研究成果，国内外学者已对其减振机理、性能和效果开展了富有成效的理论分析、数值模拟和试验研究。然而仍存在诸多不足，主要体现在颗粒阻尼器的数值模拟一般需要利用专用离散元软件或自主编程才能实现，建模难度大且计算效率低；虽然颗粒阻尼器对多层结构具有良好的减震效果，但是缺乏阻尼器布置方案的理论研究，导致并未实现颗粒阻尼器分布式减震的优势，且现有阻尼器减震效果评价方法无法细致而全面地表征其离散控制效果。上述不足导致设计人员、施工人员与业主无法有效掌握颗粒阻尼器的设计方法及准确评价其减震性能，严重阻碍了颗粒阻尼器的实际工程应用和推广。究其实质，颗粒阻尼器与受控结构之间的碰撞现象与桥梁及隔振结构的碰撞类似，已有学者对桥梁碰撞效应［23］及隔振结构的碰撞现象［24］进行了有限元模拟，这为颗粒阻尼器在通用有限元软件中的性能模拟提供了技术支持。

鉴于此，本文以PSSPD 为研究对象，通过对其减振机理及颗粒运动状态的分析，构建PSSPD 在通用有限元分析中的复合模拟单元，并讨论该单元中各参数取值，之后验证了有限元模型的精度及合理性。进一步在PSSPD 的颗粒质量、颗粒运动间距与其减震效果之间关系理论分析的基础上确定最优颗粒布置方案，并提出PSSPD 减震结构的离散减震效果的评价方法。最后通过算例分析验证了最优颗粒布置方案以及动态附加等效阻尼比评价PSSPD 离散减震效果的合理性和可行性。

2 PSSPD 模拟单元及有限元建模

PSSPD 力学模型如图2所示，图中m，k及c分别为受控结构质量、刚度与阻尼系数；mp为颗粒质量；d为颗粒运动间距。PSSPD 中颗粒运动间距与阻尼器腔体尺寸均可在实际工程中实现，更加适用于建筑结构的振动控制。由于PSSPD 中不存在颗粒间的相互作用，只有颗粒与结构之间的碰撞，这样的优势在于颗粒与受控结构之间的相互作用可以通过现有通用有限元软件模拟，下文将从PSSPD 的减振机理及颗粒运动状态着手，逐步分析在通用有限元软件中模拟颗粒运动间距、碰撞效应、摩擦效应及颗粒质量所需的单元及参数设置方法。

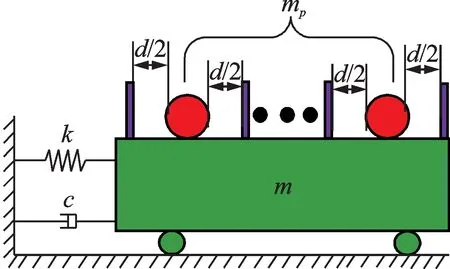
图2 PSSPD 力学模型Fig.2 Mechanical model of PSSPD

2.1 颗粒运动间距

颗粒与结构之间存在间距，当受控结构在振动时的位移超过预留间距时，颗粒与受控结构就会发生碰撞。对于该间距可以采用有限元软件中的缝（Gap）单元来模拟，如图3（a）所示，图中kp为碰撞刚度，δ0为碰撞间距。Gap 单元的力学模型为：

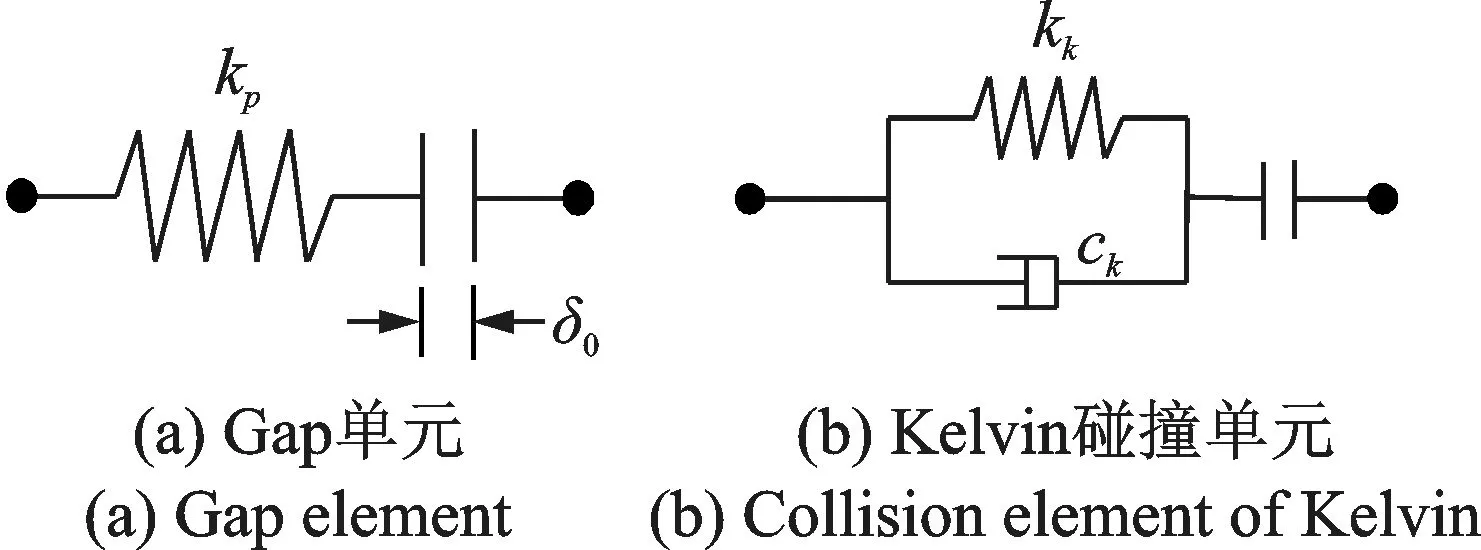
图3 有限元模拟单元Fig.3 Finite simulation element

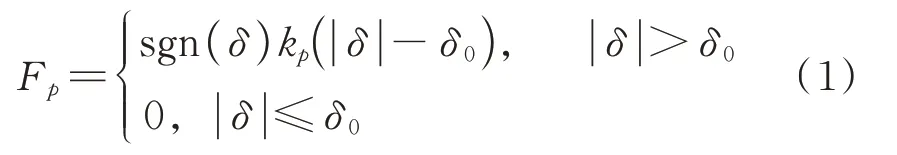
式中Fp为碰撞力，δ为颗粒与受控结构的相对运动位移，sgn(δ)=

2.2 碰撞效应

在颗粒与受控结构发生碰撞的过程中，虽然Gap 单元中可以设置碰撞刚度，但两者之间的碰撞过程实际为非完全弹性碰撞过程，该碰撞过程中应该考虑法向碰撞刚度和接触阻尼，而Gap 单元无法考虑接触阻尼的影响。文［10］的研究结果表明Hertz-damper 模型可以较准确地模拟颗粒与阻尼器腔体之间的碰撞过程。但是Hertz-damper 模型中弹性力项及黏性力项与相对侵入位移之间均为非线性关系，且恢复系数与碰撞前的相对速度相关。而在现有的有限元分析软件中仍然无法精准实现Hertz-damper 模型的模拟，且模拟过程复杂、繁琐，不易被设计人员接受。因此颗粒与受控结构之间的碰撞过程可以通过如图3（b）所示的Kevin 模型进行表征。其中Kevin 模型的接触弹性力为：

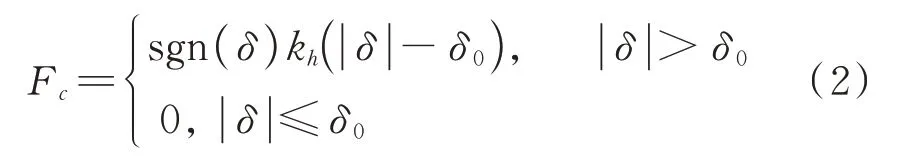
式中Fc为接触弹性力，为Kevin模型碰撞刚度，其中r为颗粒半径，与E分别为阻尼器材料的泊松比与弹性模量。

Kevin 模型中接触阻尼力为：

式中Fck为接触阻尼力，为颗粒与受控结构在碰撞时的相对运动速度，ck为阻尼系数，计算公式如下：

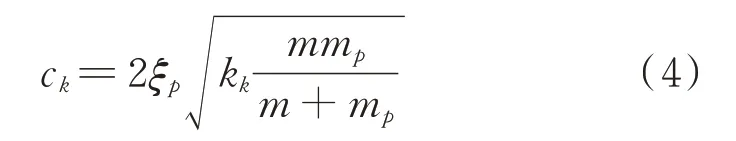
式中ξp为与碰撞恢复系数e相关的阻尼比，其计算公式为：

在通用有限元软件中，针对碰撞单元的Kevin 模型，可以在两碰撞物体之间同时设置弹簧单元和黏滞阻尼单元，单元的端点与节点完全相同，弹簧单元与黏滞阻尼单元在几何空间上形成并联状态，即成为Kevin模型。例如在SAP2000 中可以用Link 单元中的Linear单元模拟碰撞刚度，用Damper单元模拟碰撞阻尼。在该模拟过程中有两方面需要特别注意：如用Linear单元模拟碰撞刚度，则Gap 单元的作用就只是模拟颗粒的运动间距，为了消除Gap 单元中刚度对模拟结果的影响，取kp=ηkh，其中η不小于100；此外，Damper单元中的刚度应设置与Gap单元中刚度类似，也取ηkh。

2.3 摩擦效应

在颗粒与受控结构未碰撞时，颗粒受到的摩擦力包含静摩擦力、滑动摩擦力及滚动摩擦力，而当颗粒在起振之后，颗粒受到的摩擦力主要为滚动摩擦力。在现有通用有限元软件中关于摩擦力的模拟有直接模拟与间接模拟两种方法。直接模拟法如SAP2000 中的Friction isolation 单元，也可以通过摩擦阻尼器对其进行间接模拟。已有研究表明颗粒与受控结构之间的摩擦效应会降低阻尼器减震效果，但是影响较小，因此在实际工程中应该使用光滑材料，尽量减小两者之间的摩擦力，甚至消除。故在有限元模拟中可以不考虑摩擦效应的影响，这样也可以极大地方便设计人员操作。

2.4 颗粒质量

在实际工程中，颗粒的形状为球体，阻尼器的腔体为钢板，因此颗粒与受控结构之间是点与面的碰撞。若消除了颗粒与受控结构之间摩擦效应的影响，则PSSPD 中的多颗粒可以用一个质点进行模拟，便于建立有限元模型。在实际工程中用多颗粒是因为颗粒太大会影响建筑的使用空间。

综上所述，本文最终建立的PSSPD 在通用有限元中的复合模拟单元如图4所示。该单元的特点在于现有通用有限元软件均可以实现，为实现颗粒阻尼器的分布式布置及实际工程应用推广提供了必要的技术支持。但是PSSPD 减震结构体系有限元模拟的精度如何仍需进一步研究，因此下文将通过PSSPD 的数值分析方法对有限元模拟的精度进行对比和验证。

图4 PSSPD 复合模拟单元Fig.4 Combined simulation element of PSSPD

3 减震结构体系有限元模拟验证

在前文基础上，再结合PSSPD 减震结构系统性能的数值分析可对其有限元模型的精度进行验证。文［6］在剖析PSSPD 减振机理且全面考虑颗粒受力状态的基础上建立了PSSPD 性能数值分析流程，文中将不再赘述。直接利用PSSPD 数值模拟方法与其有限元模拟结果进行比较，从简谐激励与地震动激励两个方面分别检验有限元模型的合理性与精度。

3.1 简谐激励

可以从共振和非共振简谐激励两个角度对PSSPD 减震结构体系有限元模型的精度进行验证，利用SAP2000 建立的单层单跨钢结构及其详细尺寸如图5所示，受控结构参数为：m=27385.3 kg，k=28088 kN/m、阻尼比ξ=0.02 及第一周期T1=0.196 s。颗粒为实心钢珠，两种工况的相关参数选取如表1所示。表1中μ=mp/m，r为颗粒半径，np为颗粒个数，p0为简谐激励幅值，g1=ω/ωn，其中ω为简谐激励频率，ωn=此外，表1中简谐激励下颗粒运动间距是根据文［6］方法计算获得的颗粒最优运动间距。

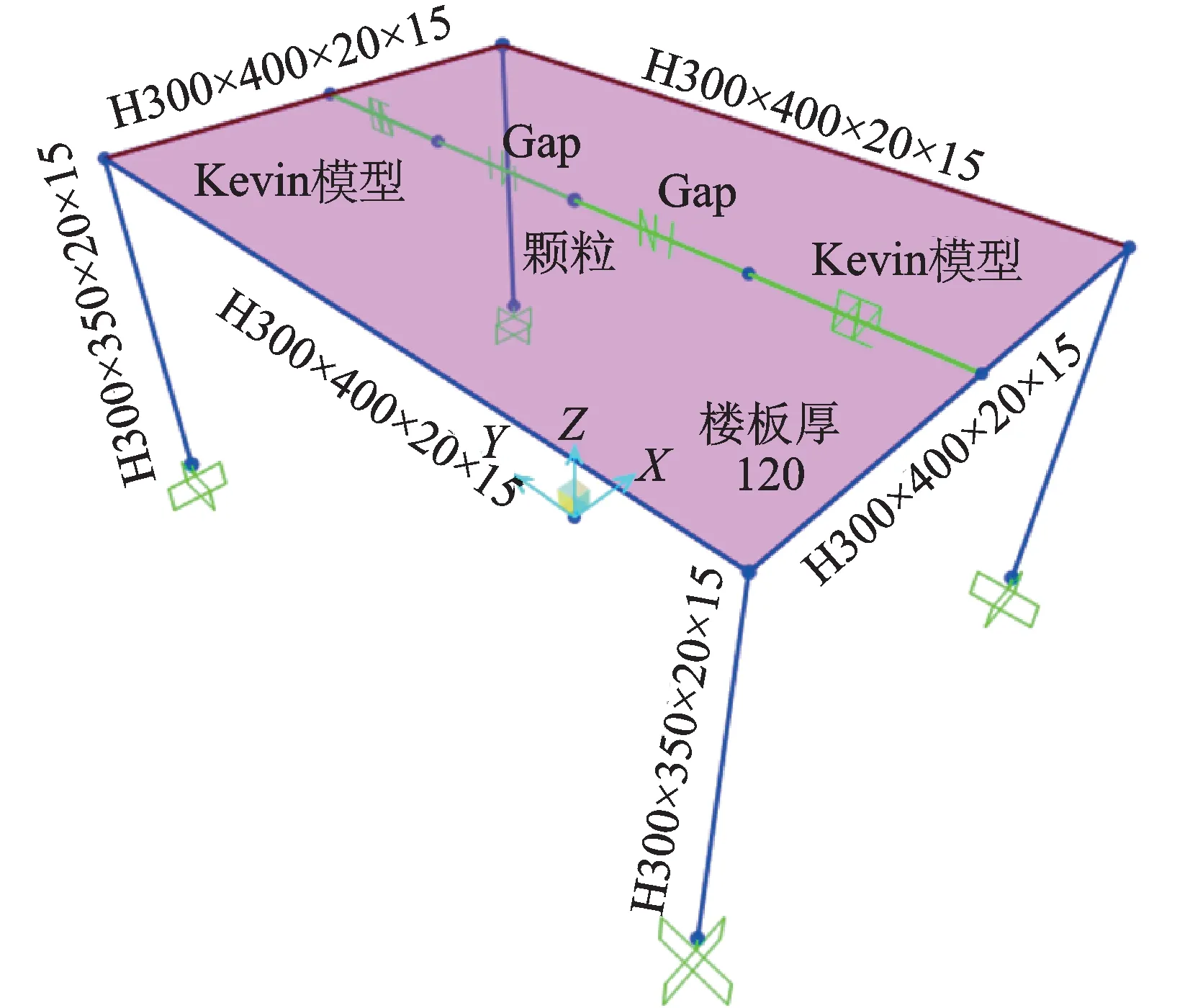
图5 受控结构有限元模型（单位：mm）Fig.5 Finite element model of controlled structure（Unit：mm）

表1 工况信息Tab.1 Case information

在选择的受控结构及颗粒参数下，通过式（1）～（5）计算获得PSSPD 减震结构体系有限元模型中各单元中参数的取值分别为：Linear 单元中kh=5.87×107kN/m，Damper 单元中刚度为100kh，ck=3772817.8 N•s/m 及速度指数为1，Gap 单元中kp=100kh及δ0=d/2。最终建立PSSPD 减震结构体系有限元模型如图5所示。两种工况下无控结构、受控结构数值分析结果及SAP2000 有限元模拟结果（FEM）如图6和7 所示。无控结构的数值分析结果与有限元模拟结果基本重合，分别计算受控结构数值分析与有限元模拟的位移峰值及速度峰值的相对误差如表1所示，其结果显示具有较高的精度。在Case Ⅰ工况下，有限元模型中Linear 单元（Fc）及Damper 单元（Fck）的受力情况分别如图8（a）和（b）所示，结果表明PSSPD 的减振机理主要为动量交换，这与文［6］的研究结论一致。为了进一步说明PSSPD 有限元模型的合理性和准确性，对其与数值分析模型在碰撞过程中的碰撞力进行对比，其结果如图8（c）所示，其中在有限元模型中，碰撞力Fp=Fc+Fck，而在数值分析模型中，虽然不能直接获得碰撞过程中的碰撞力，但是可以间接通过碰撞时受控结构的加速度值并利用牛顿第二定律获得。分析图8（c）可知两种方法计算的碰撞力数值之间尽管存在小幅误差，但是两种方法中颗粒与受控结构发生碰撞的时间基本一致，这也说明了本文有限元模拟的合理性和准确性。在数值分析模型与有限元模型中存在误差的主要原因是受控结构在数值分析中是一个集中的质量点，而有限元模拟中受控结构虽然是单层结构，但其是分布式多质点体系，因此在结构与颗粒发生碰撞的过程中碰撞效应存在差别。另外，在数值模拟中是通过恢复系数表征碰撞过程，而在有限元模拟中是通过接触单元表征碰撞过程，两种方法之间的差异也会造成结果有一定的偏差。

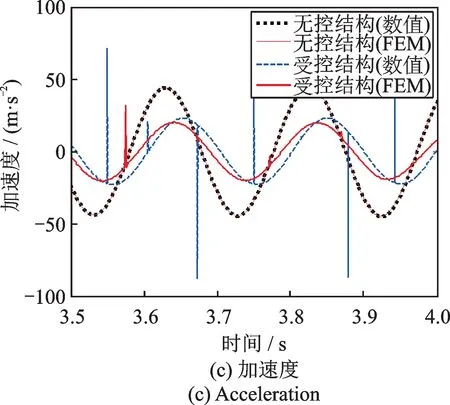
图6 Case Ⅰ时程结果对比Fig.6 Comparison time history results of Case Ⅰ

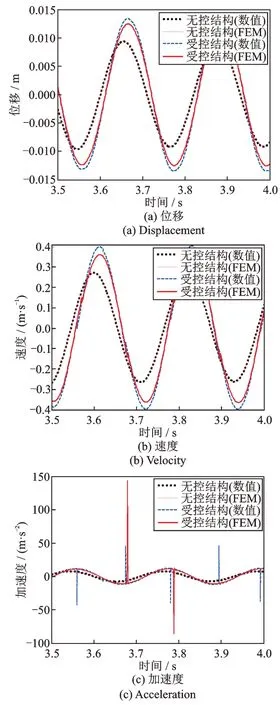
图7 Case Ⅱ时程结果对比Fig.7 Comparison time history results of Case Ⅱ

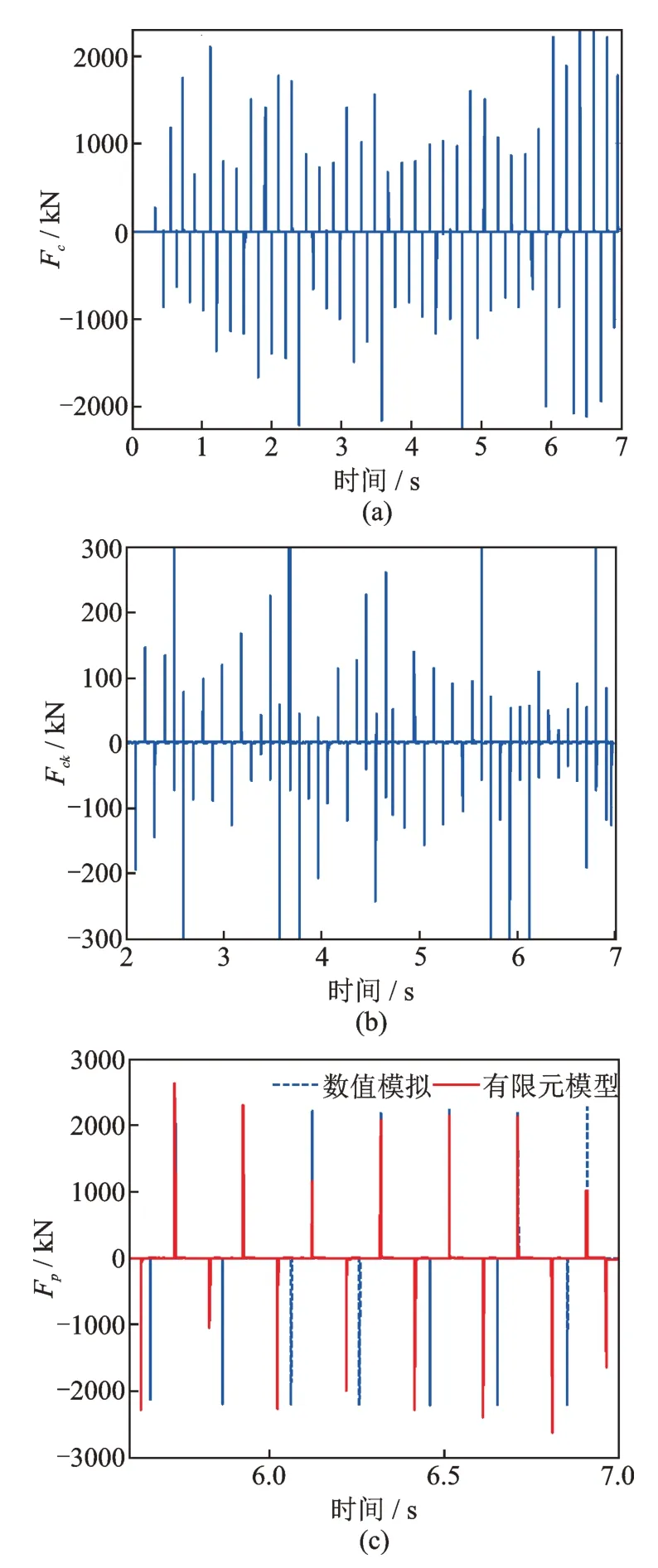
图8 Case Ⅰ工况下碰撞单元受力对比Fig.8 Force comparison of collision elements of Case Ⅰ

3.2 地震动激励

为了进一步验证PSSPD 减震结构体系有限元模拟的精度和合理性，仍以图5有限元模型及表1中颗粒为例，选取表2所示的地震动，其中表2中地震动激励下颗粒运动间距是根据文［6］计算获得的颗粒最优运动间距。分析时将地震动加速度峰值均调整至0.25g。

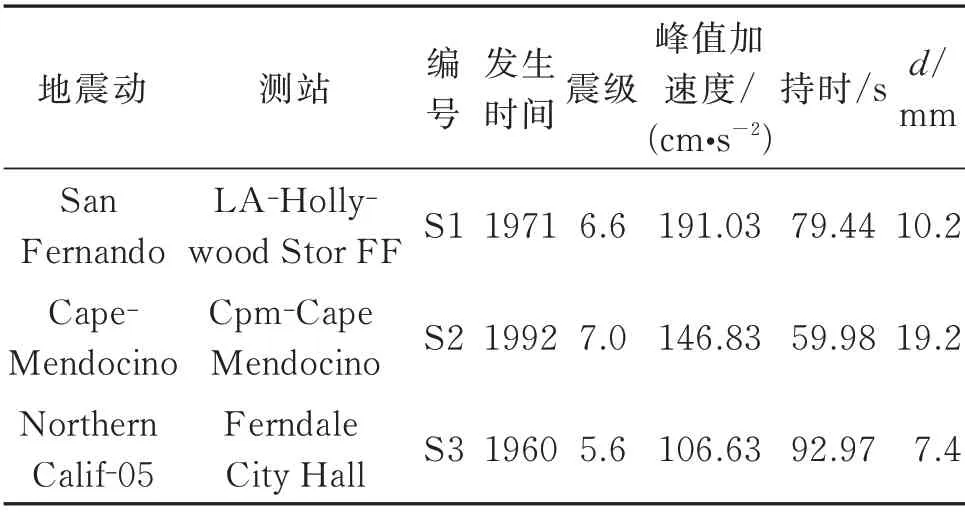
表2 地震动信息Tab.2 Ground motion information

S1 波下无控结构、受控结构数值分析时程结果及SAP2000 有限元模拟时程结果如图9所示，本文构建的PSSPD 减震结构体系有限元模型能够较好地模拟结构与颗粒之间的碰撞效应，数值分析结果和有限元模拟结果位移波形吻合、峰值接近，且两者在结构与颗粒发生碰撞的次数与时刻也比较接近，其他波的结果均与之类似。进一步计算三条地震动下的减震效果如表3所示。对比分析可得有限元模拟的减震效果比数值分析的减震效果略低，这是因为受控结构在数值分析中是一个质量点，而有限元模拟中受控结构是分布质量体系，与颗粒发生碰撞时，分布质量体系参与碰撞的质量主要是楼板的质量，导致碰撞过程中动量交换的效率较低。考虑到实际工程结构的质量也为分布式，因此通过有限元模拟得到的减震效果更加接近实际减震控制效果。

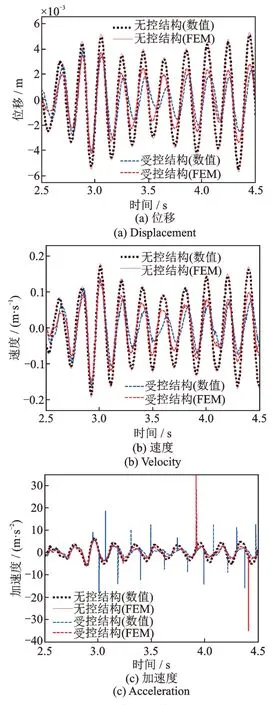
图9 S1 波时程结果对比Fig.9 Comparison time history results of S1

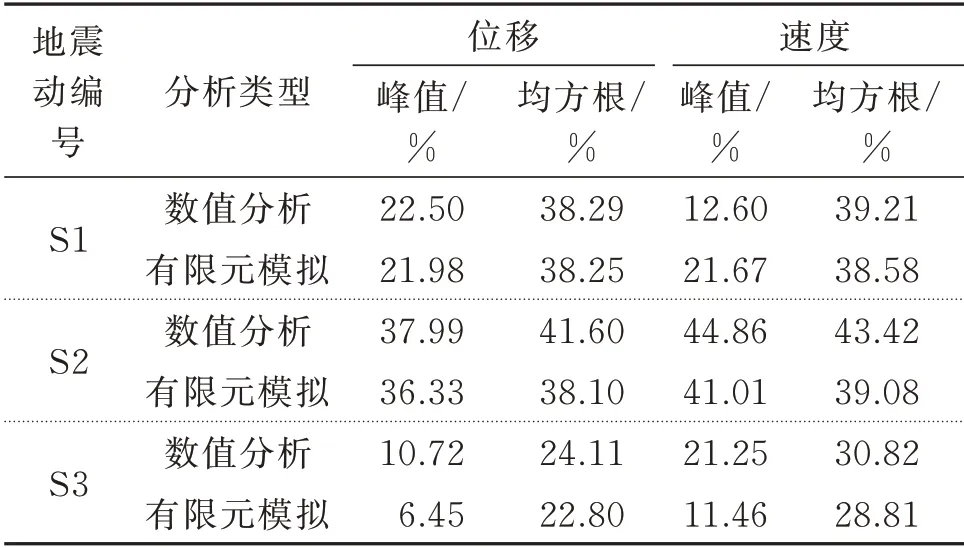
表3 减震率结果对比Tab.3 Comparison of damping rate

上述研究从时域角度对比分析了PSSPD 减震结构体系数值分析结果与有限元模拟结果的差异，为了深入剖析两者之间的差异及PSSPD 的减振机理，对数值分析与有限元模拟中无控结构的位移、受控结构的位移进行功率谱分析，结果如图10所示。图10表明PSSPD 在整个频域上均有良好的减震效果，基本不会改变结构基频，且数值分析结果与有限元模拟结果曲线的吻合度较高。在S2 波下，各单元的受力情况分别如图11（a）和（b）所示，并对数值分析模型与有限元模型在碰撞过程中的碰撞力进行对比，其结果如图11（c）所示。以上结果均表明本文提出的PSSPD 减震结构体系有限元模拟方法可行且准确，可应用于简谐激励和地震激励下的结构动力分析。下文将继续讨论如何对PSSPD 减震结构的减震性能进行设计。

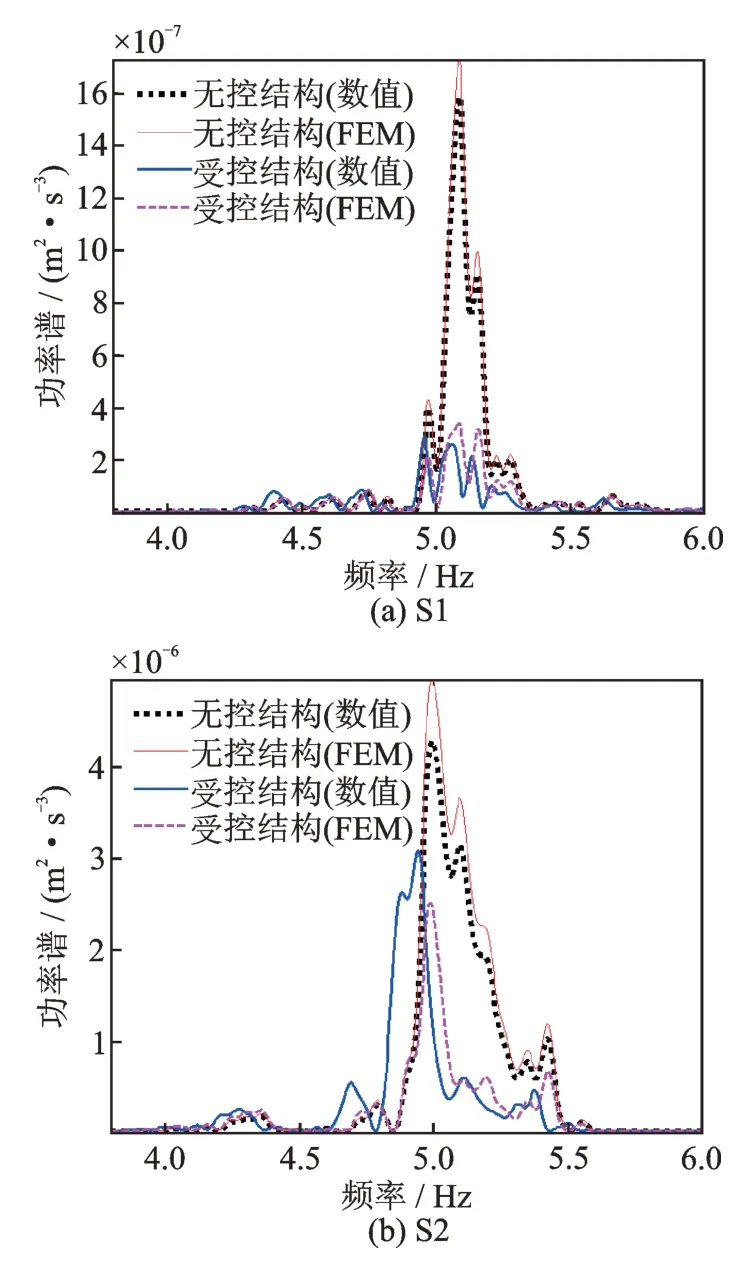
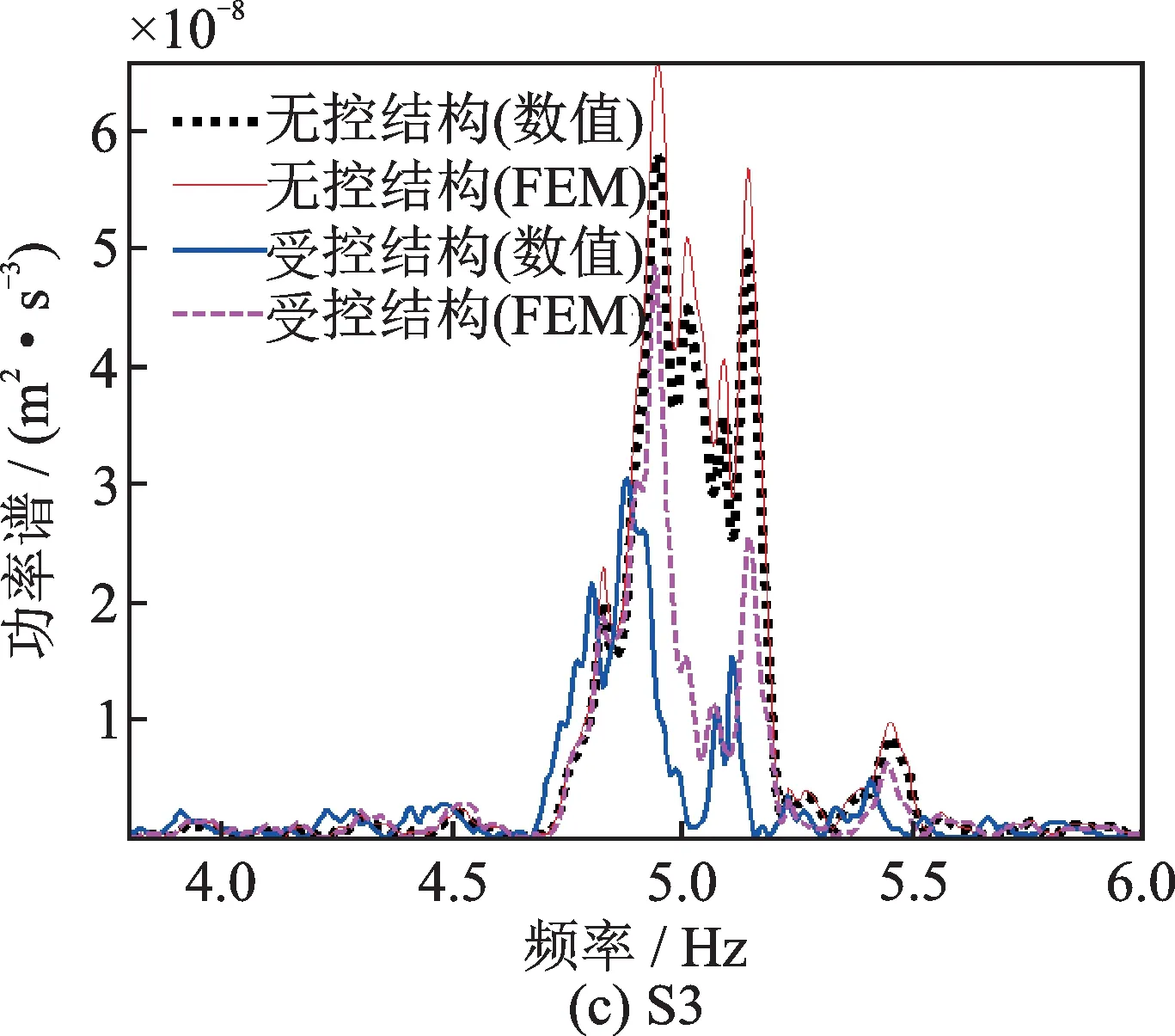
图10 地震动下位移功率谱Fig.10 Displacement power spectrum under ground motion

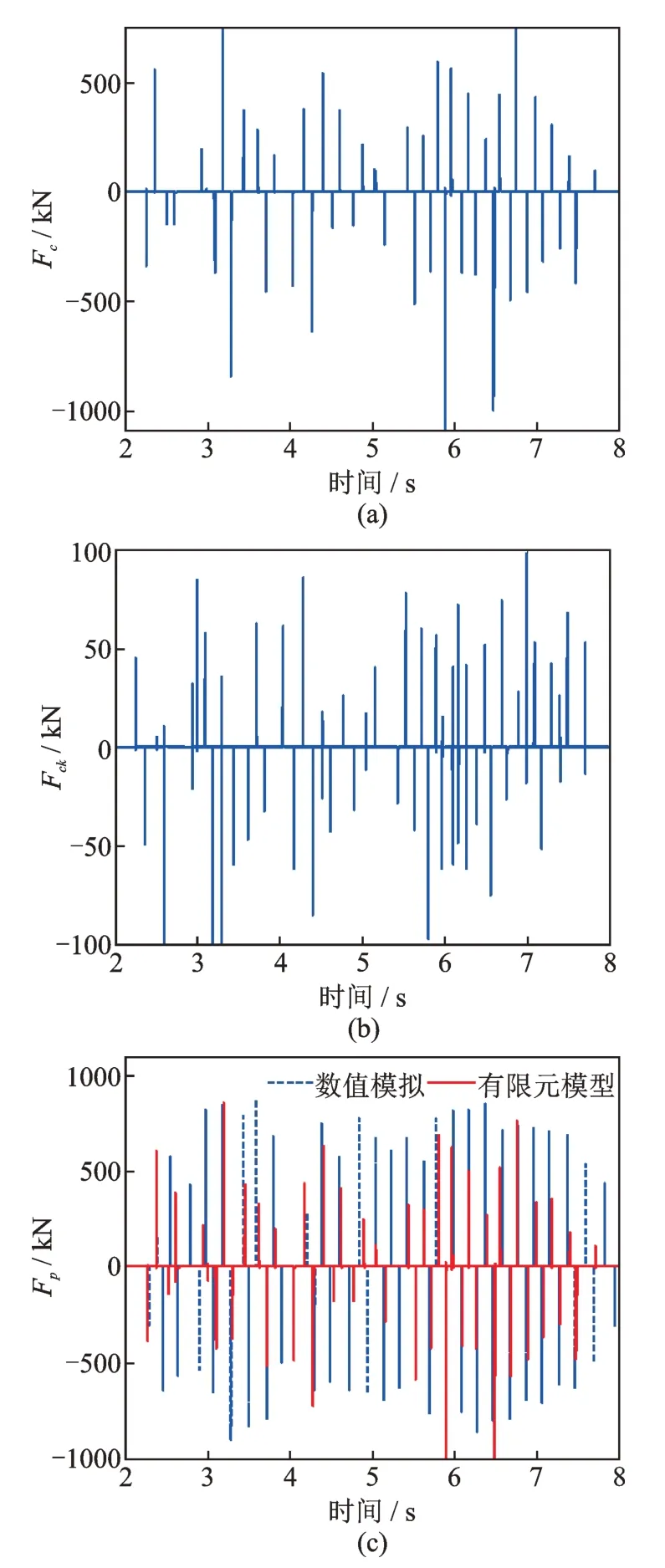
图11 S2 波下碰撞单元受力对比Fig.11 Force comparison of collision elements of S2

4 PSSPD 多自由度减震结构性能设计

PSSPD 在单层结构中的布置位置确定，而颗粒的最优运动间距也可根据文［6］中的研究结果获得。对于多层结构而言，由于其多振型的影响导致结构每层的动力响应存在差别，故不同结构层对PSSPD减振性能的需求也不尽相同。这主要体现在PSSPD 中颗粒质量在每层的分布以及相应的颗粒运动间距设置上。此外，由于PSSPD 为加速度（力）相关型阻尼器，其减振效果不依赖于结构的振型，其优化布置方法需结合力学特性综合分析。下文将探究如何对PSSPD 中颗粒质量进行优化分布并计算相应的颗粒运动间距。

4.1 颗粒质量分布

PSSPD 对受控结构的减振机理实质是通过两者的碰撞进行能量的交换，至于具有负效应的摩擦力影响可以通过工程技术手段消除。参考文［6］，可得颗粒与受控结构碰撞前后结构能量变化ΔE为：

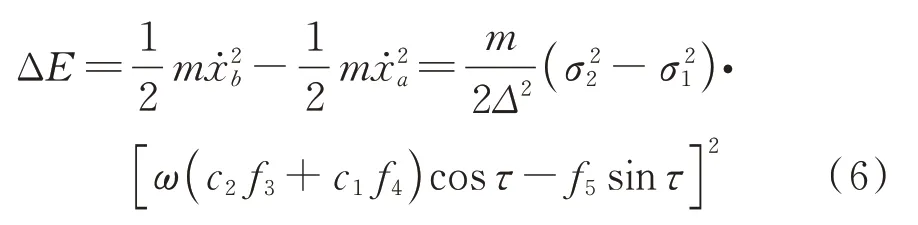
式中为受控结构碰撞前速度，为受控结构碰撞后速度，ω为激励频率，其中μ为颗粒相对结构的附加质量比。Δ，c1，c2，f3，f4，f5，τ参数中不含有颗粒质量项，具体计取值及计算方法可参考文［6］。为了更加清晰地呈现颗粒质量对碰撞前后受控结构能量的影响，本文将式（6）变换为：

由上式获得颗粒质量比对碰撞前后受控结构能量变化的影响曲线，并对两者的关系曲线进行线性拟合，如图12所示，可认为两者为正相关线性关系。多层结构在动力荷载作用下，变形越大的楼层对PSSPD 的减振需求也大，即要求颗粒转移该楼层的能量也越多。因此在多层结构中，颗粒的质量可以按照动力荷载下楼层动力响应的分布进行比例分配。关于多层结构在动力荷载作用下楼层动力响应的分布可以通过振型来表征，而在不同的动力荷载下，楼层位移存在差异。为了使颗粒质量在多层结构中的分布结论具有普遍性和通用性，振型可以通过结构模态分析选取第一阶模态结果。假设颗粒的附加质量比为μs，即μs=mp/M，其中M为多层结构的质量；多层结构的振型为z=[z1z2…zn]，则结构每层可优化布置的颗粒质量为：

图12 颗粒质量比对受控结构能量变化的影响Fig.12 Effect of μ on energy change of controlled structure

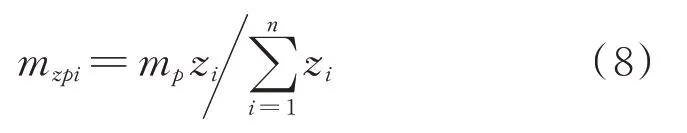
式中i表示多层结构的第i层。

为了进一步说明多层结构中颗粒质量按振型分配方式（标记为“A”）的合理性及优越性，在下文算例分析中增加了两种质量分布对比设置。对于层间刚度均匀的多层结构，在颗粒质量按振型分配的布置中，楼层颗粒质量从上到下依次减少。因此，其中一种对比设置是多层结构中颗粒质量在每层中均布方式（标记为“B”），即mapi=mp/n。另一种对比设置方式为楼层颗粒质量从上到下依次增加，可以依据多层结构第一阶模态分析结果获得层间位移的比例分配（标记为“C”），设多层结构的层间位移角为Dr=[Dr1Dr2…Drn]，则分布方式C 中结构每层布置的颗粒质量按下式计算：

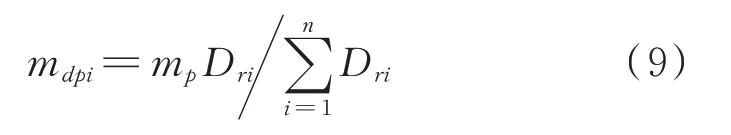
4.2 颗粒运动间距

若要使PSSPD 的减振效果达到最优，两个关键因素分别为颗粒质量与颗粒运动间距。上文通过颗粒质量对受控结构碰撞前后能量变化的影响呈现线性关系获得了颗粒质量在多层结构中的分布形式。同样，可以通过分析颗粒运动间距与颗粒质量之间的关系来指导多层结构中楼层颗粒运动间距的计算。若不计颗粒与受控结构之间摩擦效应的影响，由文［6］可知PSSPD 在简谐激励下颗粒的最优运动间距为：

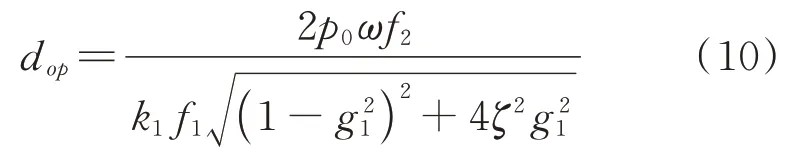
式中k1为受控结构刚度，ζ为受控结构的阻尼比，f1=σ2ωn[β(1+h2)+h1ζ]+σ1(h2θ1−h1θ2+θ1)，f2=h1(σ2−σ1)+σ1σ2[(βωn+θ1)(1+h2)+h1(ζωn−θ2)]。上述参数中只有f1中的σ1及f2中的σ2与颗粒的质量相关，其他参数的具体表达形式参见文［6］。在式（10）中颗粒质量比对颗粒最优运动间距的影响曲线如图13所示。对两者的关系曲线进行线性拟合，发现两者的关系也基本呈现线性负相关。因此，颗粒的最优运动间距与层间位移线性负相关。

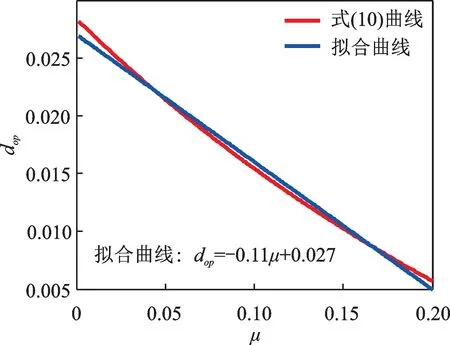
图13 颗粒质量比对颗粒最优运动间距的影响Fig.13 Effect of particle mass ratio on optimal particle motion distance

此外，颗粒的运动间距实质取决于多层结构的层间动力响应。首先需要确定所有楼层中最大的颗粒最优运动间距，可以将多自由度结构按第一阶振型等效为单自由度结构，然后利用文［6］中PSSPD在地震动中的优化分析计算出颗粒最优运动间距dopm，即为所有楼层中最大的颗粒最优运动间距。然后依据颗粒最优运动间距与层间位移呈负线性相关，计算多层结构中楼层颗粒的运动间距为：

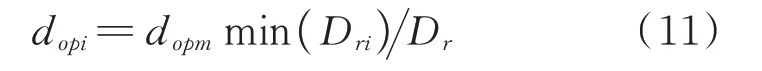
同样，为了进一步说明多层结构中楼层颗粒运动间距（标记为“a”）的合理性及优越性，在下文算例分析中增加了另外三种颗粒间距与之比较：第一种为每层颗粒的运动间距均为dopm（标记为“b”）；第二种为每层颗粒的运动间距按层间位移的比例分配（标记为“c”），如下式所示：

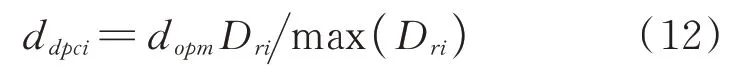
第三种颗粒运动间距是获得多层结构每层的质量、刚度以及颗粒质量，利用层间相对加速度以及文［6］的成果求得每层的颗粒运动间距（标记为“d”）。

上文中对PSSPD 在多层结构中颗粒质量分布与楼层颗粒运动间距进行了分析讨论，确定了最优PSSPD 减震结构减震性能设计方法，然而在如表4所示的3 种颗粒质量分布及4 种颗粒运动间距的布置方案中（共12 种），最优布置方案A+a 的合理性及可行性仍需验证，并且如何对PSSPD 减震结构的减震性能进行合理和准确评价也需要进一步研究。

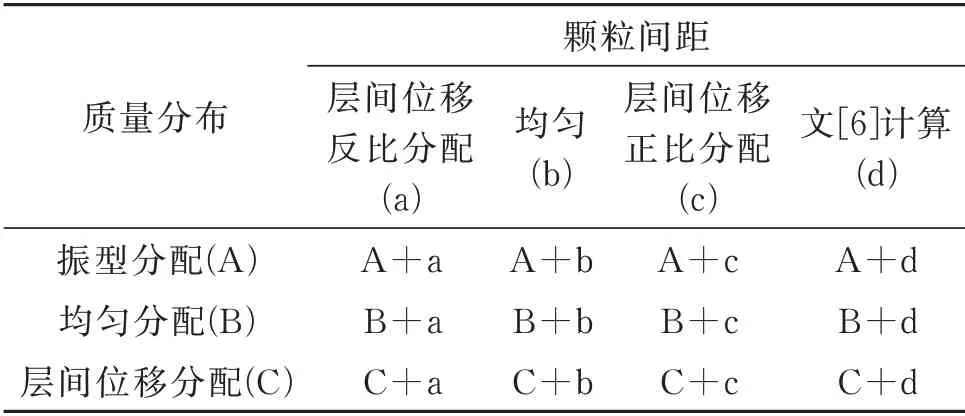
表4 PSSPD 布置方案Tab.4 Layout scheme of PSSPD

5 PSSPD 减震结构的性能评价

从能量角度分析PSSPD 减振机理，其实质就是通过碰撞对受控结构能量的耗散与转移。因此，传统阻尼器（位移型阻尼器、速度型阻尼器及调谐型阻尼器）在结构振动的时程上是能够连续工作的，而PSSPD 是对受控结构进行时域离散控制。如图2所示的PSSPD 力学模型在水平地震作用下受控结构的振动方程如下：

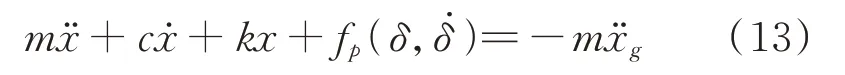
式中和分别为结构相对于地面的位移、速度和加速度；为地面加速度，fp(δ，)为颗粒与结构的碰撞力。

在地震荷载下，PSSPD 的减震效果可以用位移、速度、加速度及层间剪力等指标进行间接评价，但颗粒与受控结构在每次碰撞时转移的能量各不相同，因此其减震效果具有时变与离散的特性。对于减震结构而言，附加阻尼比是评价其减震性能最直接及全面的指标。因此本文对文［25］的研究进行改进和拓展，提出适合表征地震动下PSSPD 离散控制效果的动态附加等效阻尼比计算方法。在PSSPD 中颗粒与受控结构发生碰撞的过程中，tj-1时刻两者开始接触，tj时刻两者发生碰撞，tj+1时刻两者碰撞结束，即颗粒与受控结构的每一次碰撞经历了3 个时间步长。为了计算获得动态附加等效阻尼比，需要在时程结果中选取各局部时间段进行计算，将式（13）在地震动持时范围［tj-1，tj+1］内进行积分：

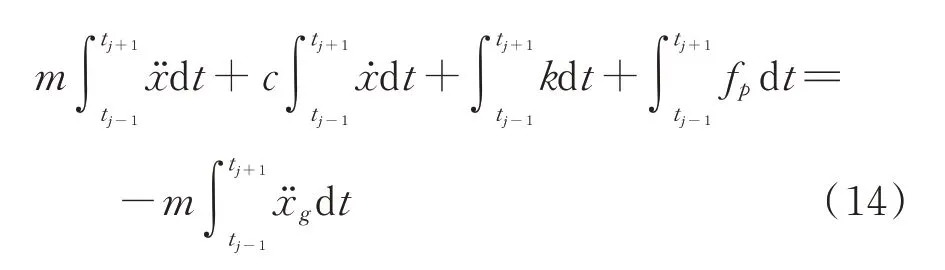
将上式写为能量的形式，可得：

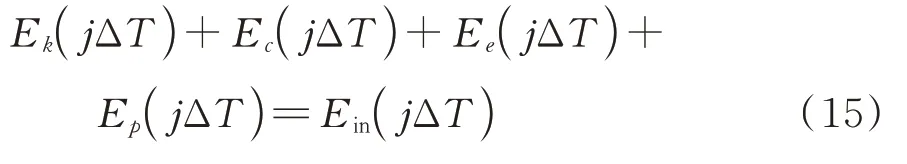
式中Ek为结构动能；Ec为结构固有阻尼耗能；Ee为结构弹性应变能；Ep为PSSPD 转移能量；Ein为地震输入能量；ΔT=tj+1−tj-1，j表示第j次碰撞。可获得PSSPD 附加在结构上的动态附加等效阻尼比为：

式中ζ0为结构的固有阻尼比。

在PSSPD 颗粒转移能量Ep的计算过程中，就是在［tj-1，tj+1］内对每层颗粒与受控结构碰撞后受控结构能量的变化值进行求和，具体的计算公式如下式所示：

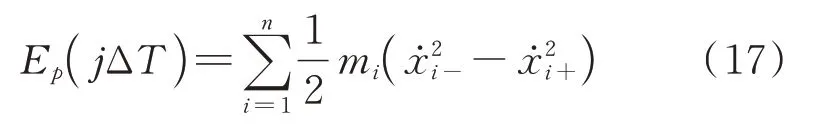
式中及+分别表示第i层结构在与颗粒碰撞前和碰撞后的速度。

为了确保PSSPD 在土木工程结构的减震控制中具有良好的减震效果，各重要参数的取值应满足下列条件：

（1）颗粒宜选用钢材，且应做防腐处理，恢复系数宜在0.4～0.8 之间。

（2）颗粒质量比的取值范围在0.5%～5% 之间，颗粒直径宜在20～60 mm 之间。

（3）颗粒最优间距在实际工程中的误差应控制在±15%以内。

（4）颗粒滑槽的直线度、平整度及光滑度应满足PSSPD 的正常工作要求，且PSSPD 与主结构之间应固结连接，保证阻尼器腔体与结构共同运动。

（5）颗粒应布置在结构质心位置，对控制结构扭转的情况，宜偏心布置，可以减轻主结构的扭转效应。具体可以选择楼板、墙体、梁和楼梯等位置。

因此，总结提出PSSPD 在多自由度结构中的设计流程如图14所示。

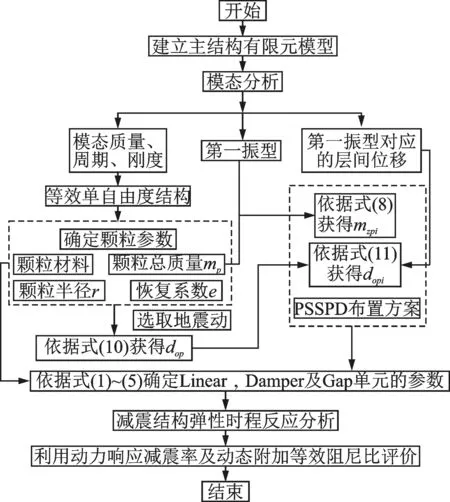
图14 PSSPD 减震结构设计流程Fig.14 Design process of damping structure with PSSPD

上文中已经验证了PSSPD 减震结构体系有限元模拟具有良好的精度并确定了颗粒的最优布置方案，也提出了评价地震动下PSSPD 离散减震效果的方法与性能设计流程，下文将结合具体算例进一步验证最优布置方案的合理性及对PSSPD 减震结构的减震性能进行评价。

6 算例分析

为了验证PSSPD 在多层结构中最优布置方案的合理性与最优性及其在地震动下对多层结构的减震效果，以一典型钢框架结构为例进行分析。该结构共9 层，层高均为4 m，跨度均为6 m，其中钢梁的横截面为H 形，其型号为W36×135；钢柱的横截面也为H 字形，其型号为W14×665；楼板厚度为120 mm，上述构件钢材均为Q345。建立该结构的有限元模拟如图15所示，各材料的属性直接使用SAP2000 软件中的默认本构。该结构8 度抗震设防，场地类别为Ⅱ类，抗震等级为一级。设计地震分组为第二组，设计基本地震加速度值为0.20g。

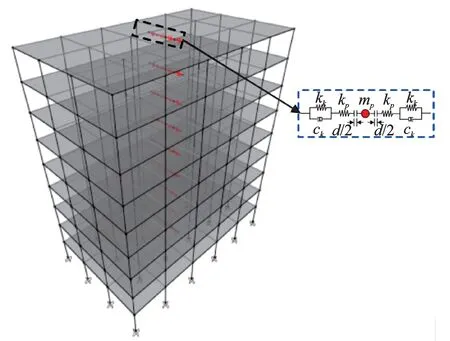
图15 9 层钢框架结构有限元模型Fig.15 Finite element model of 9-storey steel structure

首先对该钢框架结构进行模态分析，可获得其模态质量为M=5.19×106kg，第一阶模态沿短轴方向振动，周期为T=1.098 s，第一阶模态所对应的刚度K=1.70×105kN/m，结构的振型阻尼比为0.02；楼层质量mi=5.77×105kg，通过试算层间刚度使其结果与第一阶周期相同，可获得层间刚度ki=1.75×104kN/m。通过分析获得第一阶振型及相应的层间位移角的分布情况如图16所示，图中两者结果均进行了归一化处理。

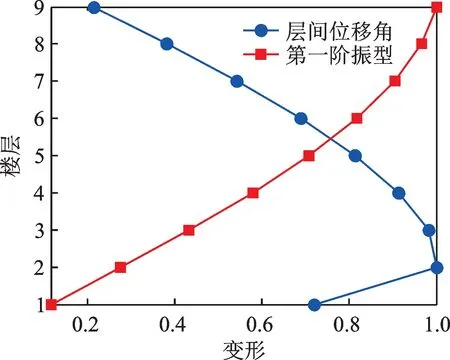
图16 无控结构变形Fig.16 Deformation of uncontrolled structure

在上述获得无控结构动力特性之后，选取2 条实际地震波及1 条人工波进行PSSPD 最优布置方案的验证，其中2 条实际地震波可以选取表2中的S1 波和S2 波，人工波按照二类场地生成即可，并标记为“RG”。分析时将所有地震动加速度峰值均调整至0.25g。颗粒的信息如表1所示，按本文第4 节PSSPD 减震结构减震性能设计可获得不同PSSPD布置方案下颗粒质量分布与楼层颗粒运动间距，如表5和6 所示。

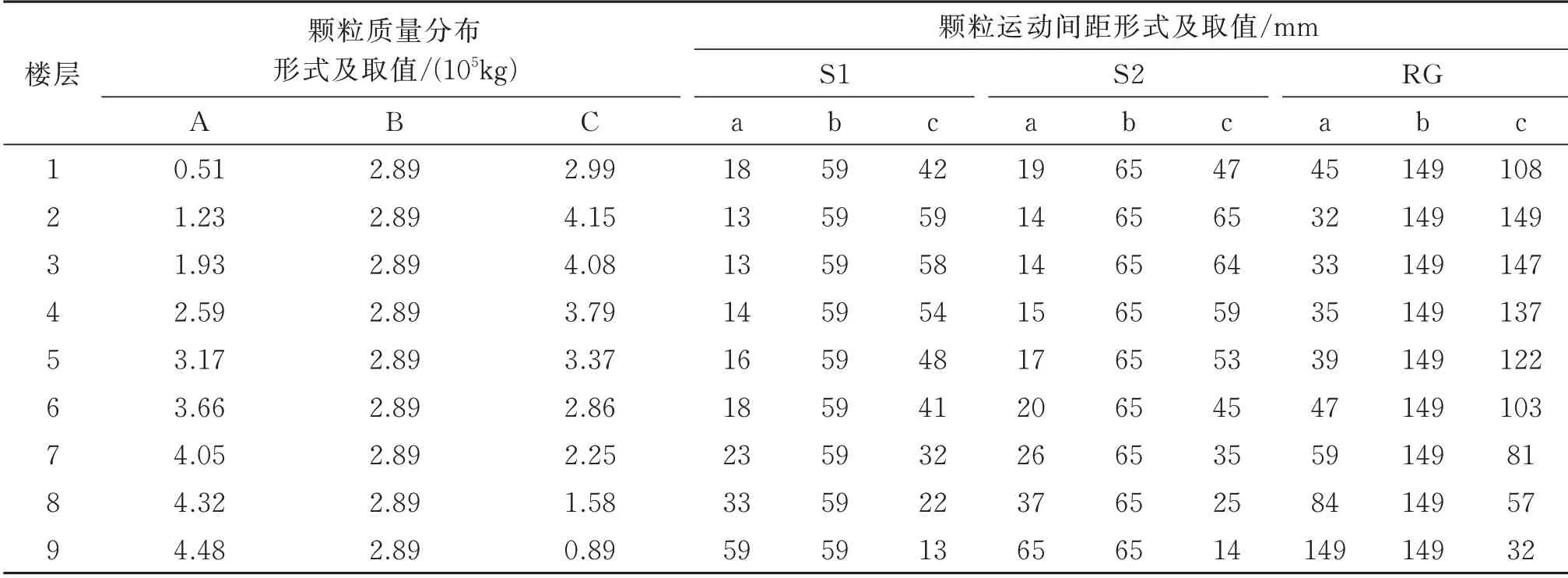
表5 PSSPD 布置方案信息Tab.5 Layout scheme information of PSSPD

最终在SAP2000 中建立相应的PSSPD 减震结构体系有限元模型如图15所示。对每条地震波及每种布置方案下PSSPD 的减震效果进行分析，并以地震动下受控结构楼层位移及速度的平均减震率来评价其减震效果，其中各布置方案下楼层位移（速度）峰值及均方根平均减震率如图17～19所示。

图17～19 对不同的PSSPD 布置方案进行了减震效果对比，结果表明当楼层颗粒运动间距按a 设置时在不同的颗粒质量分布下均取得最优减震效果。进一步对楼层颗粒运动间距按a 设置下的三种颗粒质量分布进行对比，如图20所示。结果表明PSSPD 在颗粒布置方案A+a 下确实取得最优减震效果，证明了前文中颗粒质量分布与楼层颗粒运动间距取值理论分析的正确性和合理性。该方案下PSSPD 对受控结构每层楼均有良好的减震效果，并且其对所有楼层的最高减震率与最低减震率相差在4%以内，证明了分布式PSSPD 减震性能的优良性和鲁棒性，这是对各楼层的颗粒质量及颗粒运动间距优化的结果，也说明了颗粒质量与颗粒运动间距在楼层中的分布对PSSPD 减震效果影响的重要性。

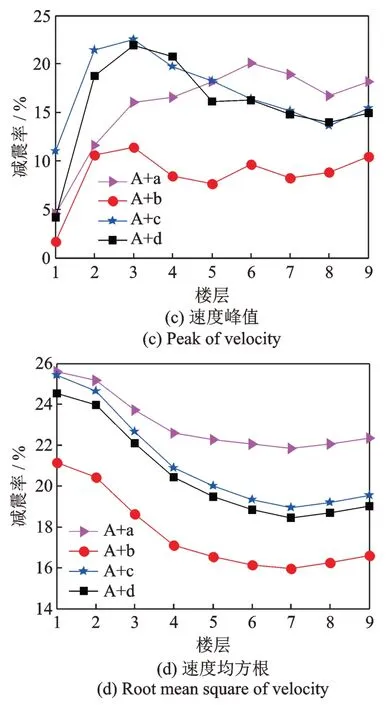
图17 颗粒质量振型分配（A）时的减震效果Fig.17 Damping effect of particle mass distribution by vibration mode（A）

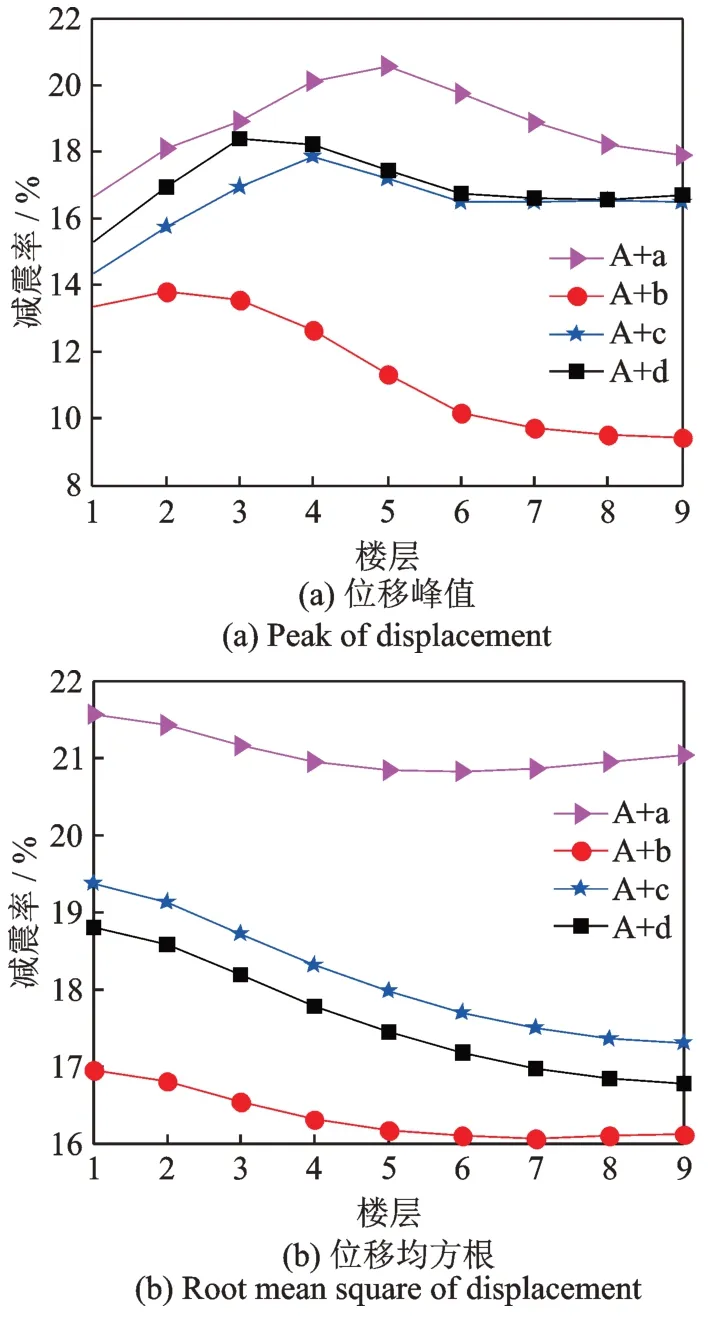
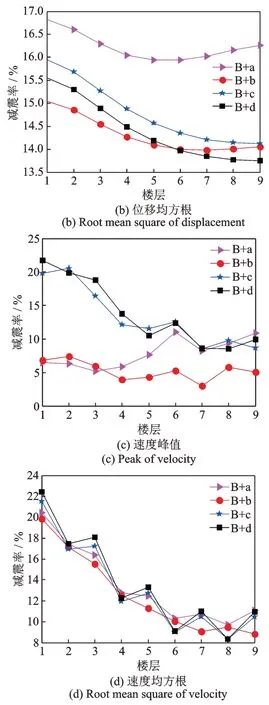
图18 颗粒质量均匀分配（B）时的减震效果Fig.18 Damping effect of particle mass distribution by evenly distributing（B）

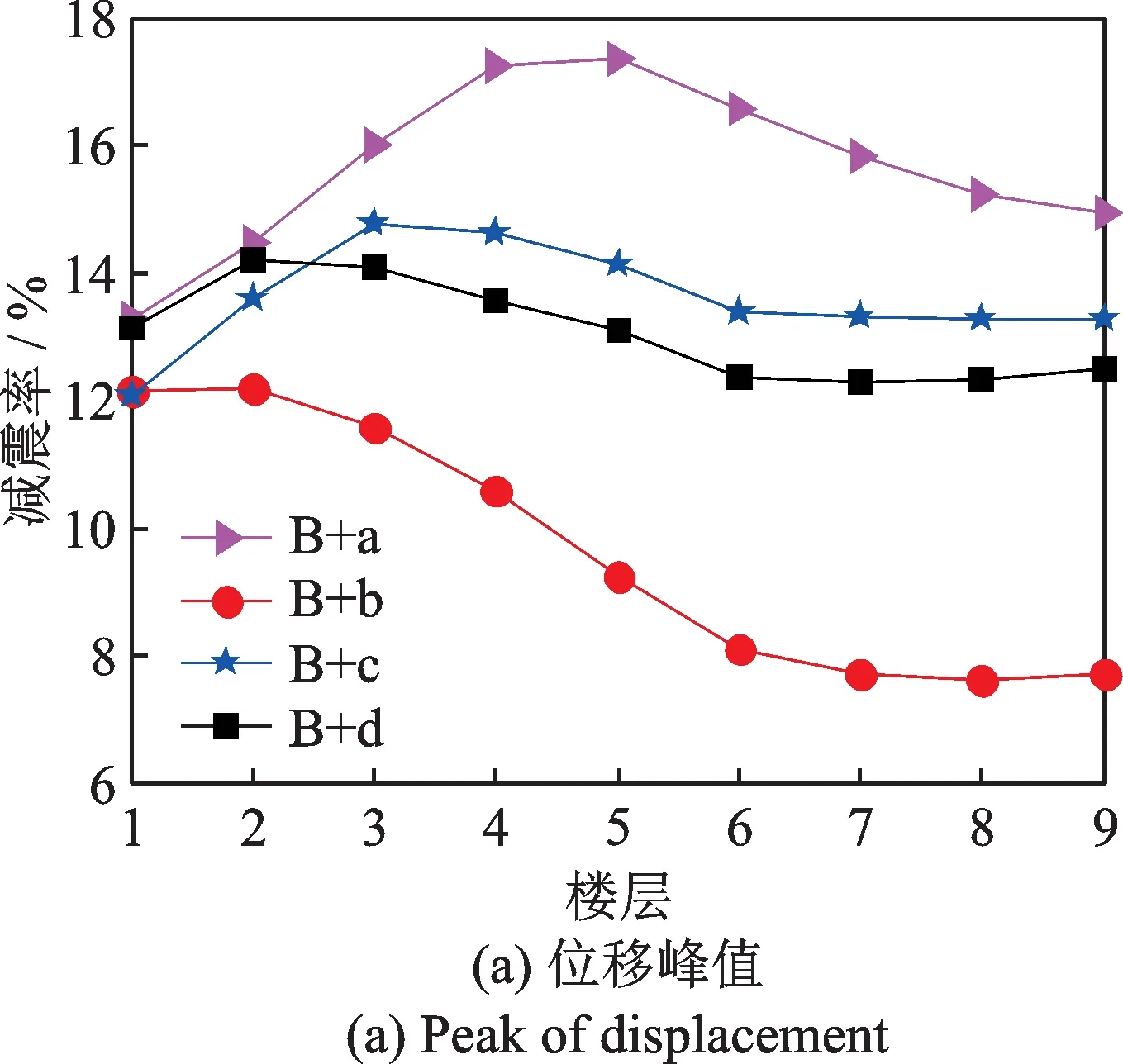
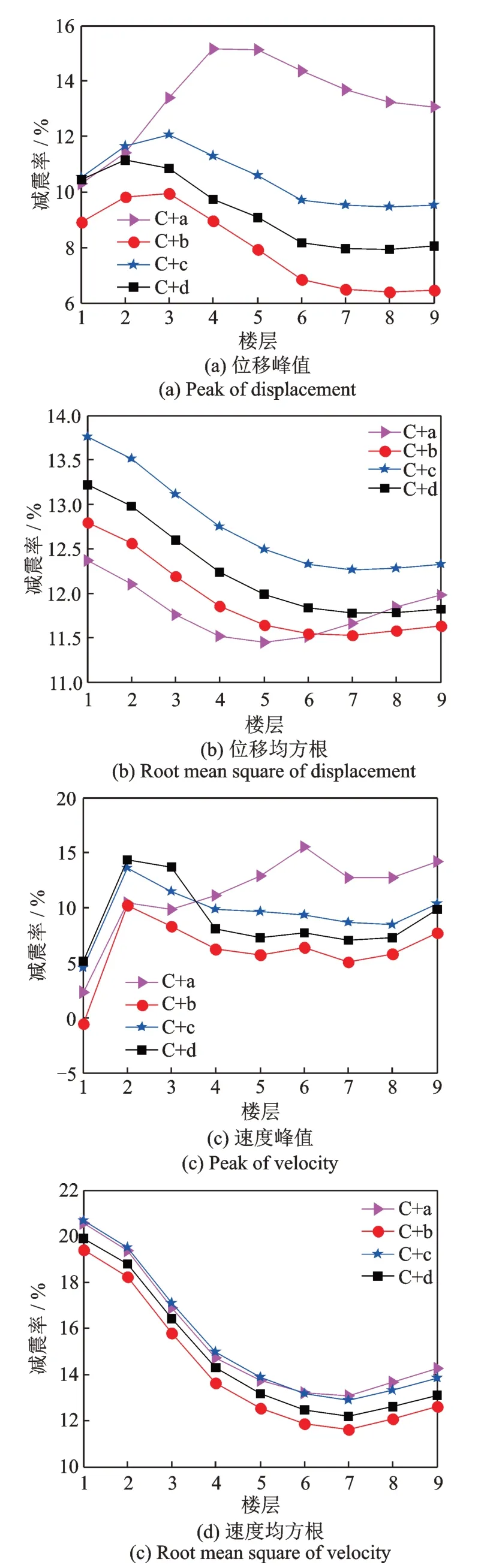
图19 颗粒质量层间位移分配（C）时的减震效果Fig.19 Damping effect of particle mass distribution by interlayer displacement（C）

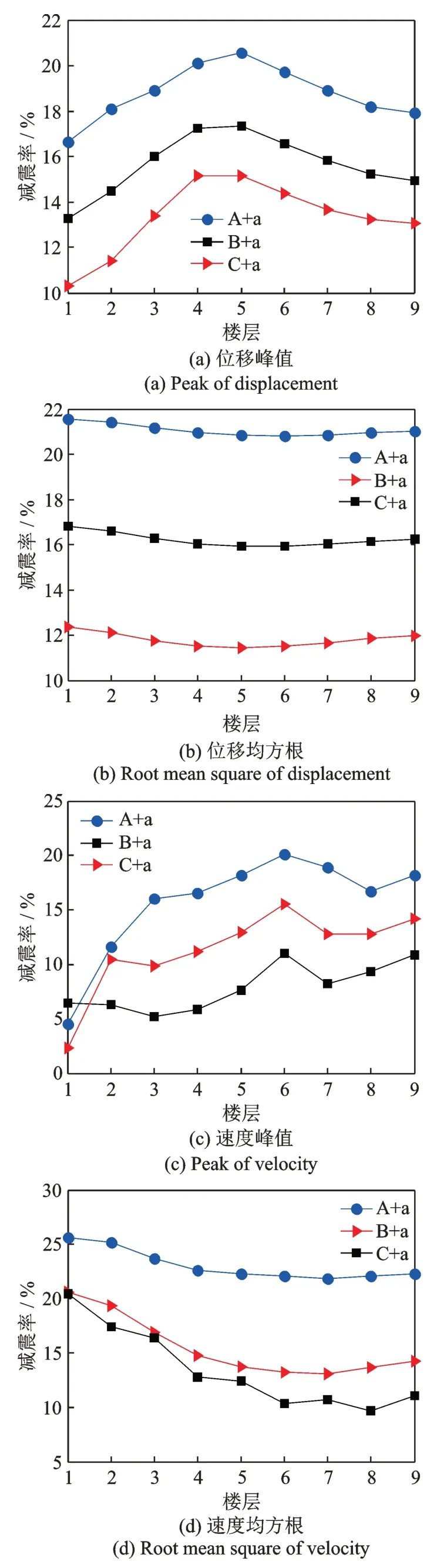
图20 PSSPD 布置方案综合减震效果比较Fig.20 Comparison of comprehensive damping effect of PSSPD layout schemes

表6 文［6］计算颗粒运动间距（d）/mmTab.6 Calculation of particle movement distance in reference［6］（d）/mm

为了直观且全面地表征PSSPD 对受控结构的减震效果，采用本文提出的计算地震动下PSSPD 动态附加等效阻尼比的方法对其减震性能进行评价，当楼层颗粒运动间距按a 设置时，三种颗粒质量分布下PSSPD 在S1 波作用时动态附加等效阻尼比的计算结果如图21（a）所示。结果表明PSSPD 在碰撞瞬时能够提供较大的附加等效阻尼比，所以对受控结构的位移和速度具有良好的控制效果，其他地震波的结果与之类似。

虽然图21（a）的结果能够细致全面地体现PSSPD 的离散减震效果，但是三种布置方案减震效果的差异仍不够清晰。为了弥补该不足，可以选取一定时间段内的附加等效阻尼比求平均值，即用该时间段内的附加等效阻尼比之和除以颗粒与受控结构碰撞的次数可获得PSSPD 平均动态附加等效阻尼比。若取三条地震动的时间段均为0.6 s，S1 波作用下PSSPD 平均动态附加等效阻尼比如图21（b）所示。平均动态附加等效阻尼比能够体现出三种PSSPD 布置方案时变减震效果的差异，并且布置方案A+a 有明显的减震优势。结合地震动的加速度时程曲线分析可知，在地震反应剧烈时，PSSPD 的附加等效阻尼比较大，这是因为地震动越剧烈受控结构的动力响应就越大，颗粒与受控结构之间转移的能量也就越多。此外，也可通过动态附加等效阻尼比之和除以总碰撞次数获得在整个时间历程上PSSPD 的平均减震效果，如图21（c）所示。该结果进一步凸显了PSSPD 最优布置方案A+a 的合理性和可行性。

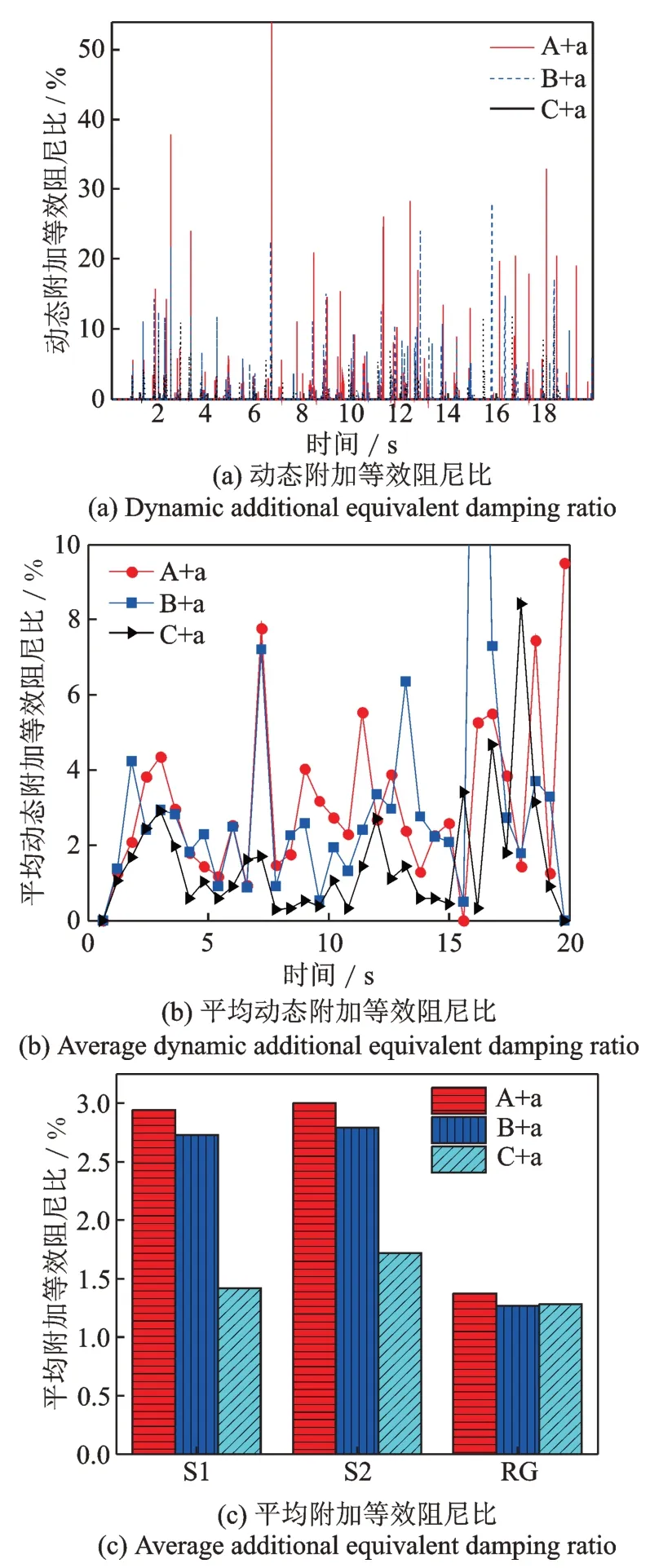
图21 PSSPD 减震效果评价Fig.21 Evaluation of damping effect of PSSPD

通过算例分析可知PSSPD 在颗粒质量振型分布及楼层颗粒间距层间位移反比分配的组合方案下减震效果达到了最优，其减震率高达25%，具有良好的工程应用价值。在PSSPD 减震结构的减震性能评价中，离散附加等效阻尼比能够细致且准确地表征PSSPD 的减震效果，而平均附加等效阻尼比能够显著体现不同PSSPD 布置方案减震效果的差异。

7 结 论

为了弥补目前PSSPD 减震结构在有限元模拟中的空白及其减震性能评价的不足，本文通过对其减振机理及颗粒运动状态的分析，构建了PSSPD 在通用有限元中的复合模拟单元，确定了PSSPD 在多层结构中的最优布置方案，并提出了减震结构的减震性能评价方法及设计流程，继而对PSSPD 在多层结构中的布置方案及减震效果进行了深入研究。得到的主要结论为：

1）通过深入剖析PSSPD 的减振机理及颗粒的运动状态，用Gap 单元、Linear 单元、Damper 单元和集中质量形成的复合单元对PSSPD 的减振性能进行模拟，并与数值模拟结果进行对比分析，验证了复合单元模拟PSSPD 减振性能的合理性、可行性及准确性。

2）基于对颗粒质量、颗粒运动间距及PSSPD减震效果之间关系的理论分析，确定了颗粒质量按振型分布及颗粒运动间距按层间位移反比分布的最优布置方案，通过不同PSSPD 布置方案减震效果的对比，证明了最优布置方案的合理性和可行性。

3）通过对PSSPD 减震结构碰撞过程及其能量变化的分析，提出了地震动下PSSPD 离散控制效果的动态附加等效阻尼比计算方法，该方法能够全面而细致地评价PSSPD 减震结构的减震性能。

4）PSSPD 减震结构有限元模拟的分析结果表明PSSPD 能够有效减轻受控结构楼层的动力响应，且具有灵活布置、鲁棒性强和可更换等特点。