面向多性能目标的广义肘节机构优化设计方法及减震应用

何浩祥，兰炳稷，陈易飞，吴 山

（北京工业大学工程抗震与结构诊治北京市重点实验室，北京 100124）

引 言

在中小震或强风下，工程结构的层间位移较小，传统的位移相关型和速度相关型阻尼器难以充分发挥作用，减震效率偏低。通过位移放大机构提高减震效率即为一种良好的改进方案［1-6］，肘节式位移放大机构作为一种构造简单、成本低廉的变形放大装置被广泛研究与应用。Constantinou 等［7］提出了初始状态下阻尼器及其支撑与下连杆垂直的肘节机构，推导了肘节相对初始位置有微量侧移时阻尼器轴向变形与肘节侧移量间的比例关系，本文称其为位移放大系数的小变形解。该机构的上、下连杆与结构连接位置分居结构层顶与层底，占据空间较大，在应用时有一定局限。Hwang 等［8］改进了肘节机构的几何构造，本文称为传统肘节机构，并推导了其位移放大系数小变形解，但该机构仍需占用较大空间。此后传统肘节机构成为研究主流，位移放大系数小变形解更是成为肘节机构的唯一性能描述参数，但位移放大系数小变形解并不能反映肘节机构随侧移量变化时位移放大能力的时变特性。尽管一些研究者［9-11］进一步推导了大偏移时阻尼器轴向变形与肘节侧移间的比例关系（本文称之为位移全量放大系数），且部分反映了时变特性，但其并非对肘节机构位移放大能力的直接描述。鉴于肘节机构性能的复杂性与性能描述参数的不完备性，目前尚未能建立其位移放大能力的评价标准，以此为基础的几何参数优化研究更是少见。赵昕等［12］以最大化位移放大系数小变形解为目标对传统肘节机构的几何构造进行迭代寻优，但在约束条件与优化目标选取上缺乏依据，且不易直接指导工程设计。有鉴于此，完善肘节机构性能描述参数与评价标准，并据此提出适用于肘节机构的几何优化设计方法成为亟需解决的理论和工程问题。

优化肘节机构位移放大能力旨在提高耗能元件效率，黏滞阻尼器是目前肘节机构中最常使用的阻尼元件，而附加等效阻尼比则是量化与评估减震体系耗能效果的重要指标。采用应变能法［13］、自由振动衰减法［14］与模态耗能法［15］均可求解耗能体系的附加等效阻尼比。应变能法理论假设存在局限，计算精度偏低，但因其可根据目标附加等效阻尼比方便地估算肘节机构中的黏滞阻尼器参数，因而在相关减震方案设计中得到广泛应用。自由振动衰减法的适用范围有限，难以推广，在应用性方面存在缺陷。模态耗能法根据结构自身模态阻尼耗能与阻尼器耗能的比例关系计算阻尼比，机理明确且严谨，适合推广，但尚不能细致反映阻尼比的动态演变过程，可对其进行拓展，以便为计算地震作用下减震体系的时变附加等效阻尼比提供技术支持。

针对上述问题，本文首先拓展了传统肘节机构的形式，提出广义肘节机构形式。其次，针对广义肘节机构提出位移增量放大系数概念，并基于此进一步给出肘节机构位移放大能力的标准与简化参数，为广义肘节机构的几何构造优化提供理论基础与实现方法。基于增量位移放大系数的性质研究了肘节机构耗能能力随侧移量的变化规律，提出了肘节机构耗能的简化计算参数，改进了基于应变能法计算肘节机构附加等效阻尼比的理论。最后结合时变阻尼比与上述成果提出了面向多级性能设防目标的广义肘节机构减震方案优化设计方法。

1 广义肘节机构及其位移增量放大系数

1.1 传统肘节机构与广义肘节机构

传统肘节机构如图1所示，其上、下连杆与结构连接处分居层顶与层底，占用空间较大。针对其不足，本文提出广义肘节机构，构造如图2所示，其上、下连杆与梁、柱连接处位置可依据建筑结构空间需求予以确定，布置灵活且节省空间，而传统肘节可视为广义肘节机构的一种极端形式。此外，肘节机构根据自身与梁、柱所呈四边形的凹凸性可分为凸肘型与凹肘型。凸肘型如图1（a）与图2（a）所示，凹肘型如图1（b）与图2（b）所示。

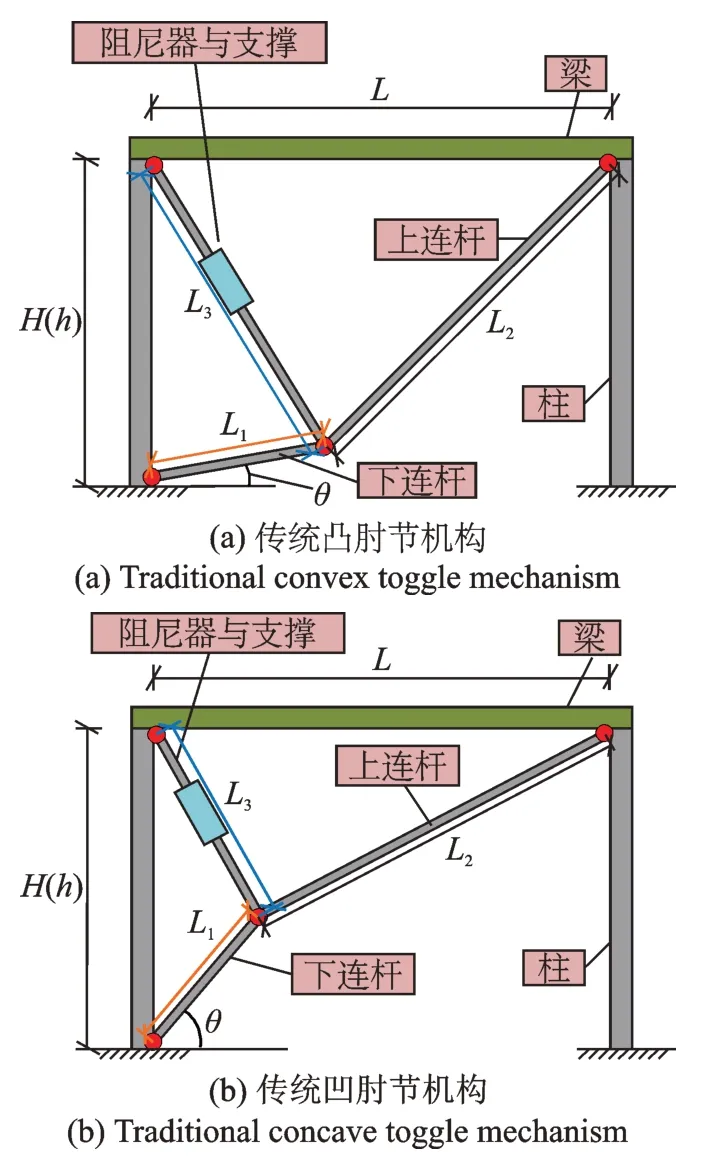
图1 传统肘节机构Fig.1 Traditional toggle mechanism

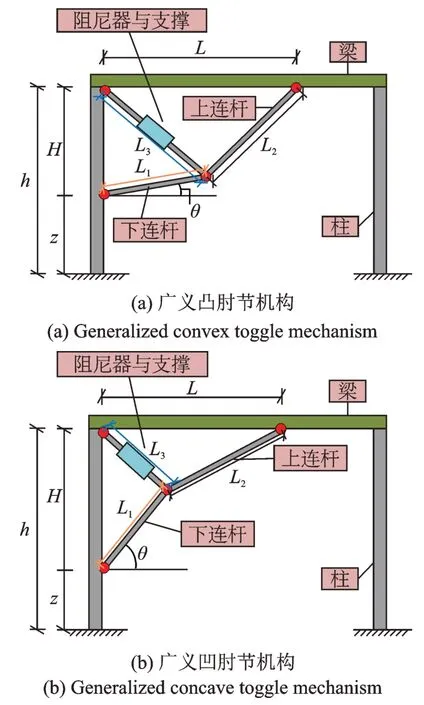
图2 广义肘节机构Fig.2 Generalized toggle mechanism

1.2 广义肘节机构位移增量放大系数

对于如图2所示的广义肘节机构，框架区格高度为h，下连杆端部距柱底的距离为z，上连杆端部、下连杆端部至阻尼器支撑和结构连接处的距离分别为L和H，下连杆与水平线夹角为θ，上连杆长度为L2，下连杆长度为L1，无层间位移（初始状态）时阻尼器与支撑总长为L3。当框架产生侧向变形时，广义肘节机构上、下连杆端部水平相对距离产生变化，进而带动梁、柱与上、下连杆所组成的四边形对角线长度发生变化，随即阻尼器发生轴向变形并耗能。若定义肘节机构上、下连杆端部间水平相对距离较初始状态改变量为u时阻尼器相对初始长度变形量为Δd，且u在两点相对距离变大时取正，则|Δd/u|即为位移全量放大系数，记为fq，而fq在u趋近于0 时的极限值即为位移放大系数小变形解fs。因而位移全量放大系数为小变形解在u定义域内的推广，表现了肘节机构位移放大能力的时变特性，但其是对于（0，u）区间内机构位移放大能力的平均反映，以该值直接描述或评价肘节机构位移放大能力是不直观且不恰当的。有鉴于此，引入位移增量放大系数d，其定义为Δd关于u偏导数的绝对值。d更为直观的物理意义为肘节机构发生单位侧移时阻尼器的轴向变形量，该系数描述了肘节机构在u定义域内任意一点的位移放大能力，是描述位移放大能力的良好指标，可依据侧移区间内d的幅值直接判断位移放大能力强弱。若设机构侧移为u时θ值变化为θ*，且假设结构侧移时肘节机构上、下连杆及梁柱所构成四边形各边两端点间距离保持不变，则上述位移放大系数可由下式计算；

式中A=H2+L（L+2u）−（L1−L2）2，B=H2+L（L+2u）−（L1+L2）2，C=H2+L2+2Lu+L12−L22，D=−i（H2−u2）0.5+L+u，i 为虚数单位。需要说明的是，梁的挠曲变形也会对fq与d产生影响，可将上连杆与梁连接处的竖向位移等效为u的变化，从而利用式（1）进行求解，但其值在风或地震作用下幅值较小，且呈强随机性，难以准确量化。

式（1）描述了机构侧移与阻尼器轴向变形间的定量关系，对于广义肘节机构，其层间位移放大能力与相联柱的侧向变形模式直接相关，可假定机构侧移与层间位移间存在恒定的比例关系，并定义该比例关系为层间位移利用率γ，其值主要由机构相联柱所在楼层、柱端约束情况及下连杆与柱的连接高度等因素确定，可依据改进D值法进行求解，具体计算如下式：

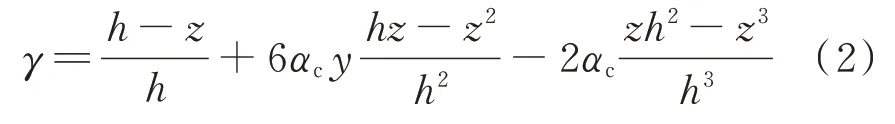
式中h为层高，y为柱反弯点高度占层高的比例，αc为侧向刚度折减系数，具体求解方法可参见文献［16］。需要注意的是，采用上式求解γ时忽略了下连杆轴力对柱侧移形态的影响，但经大量模拟分析表明式（2）具有较高精度。若设层间位移量为U，则广义肘节机构所利用侧移量为u=Uγ，将其代入式（1）即可得到层间位移全量放大系数Fq与层间位移增量放大系数D的解析解，具体计算如下式所示；

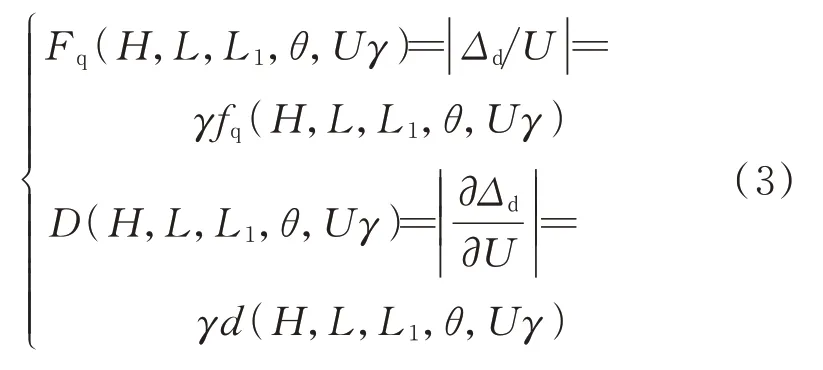
由式（3）可知，广义肘节本身的位移放大系数与层间位移放大系数间具有简单的转换关系，因此下文仅对广义肘节机构的位移增量放大系数d做进一步研究。

1.3 广义肘节机构的几何约束条件

当肘节上、下连杆与结构连接处间相对水平距离增大时，连杆会趋于拉紧并存在被拉断的风险，因而有必要明确广义肘节机构侧移限值对其几何参数的约束。若设广义肘节机构u的最大侧移限值为umax，则根据几何关系可推知广义肘节位移放大机构的θ应符合如下式所示的约束条件：

式中E=Lumax，F=L1（H2+L2+2Lumax）0.5。显然当上、下连杆与结构连接处相对水平距离减小至一定程度时，广义肘节机构也将失效，但此时侧移量绝对值远大于umax，因而可不予考虑。根据式（4）可知，当广义肘节机构长度参数确定时，umax的值越小，广义凸肘节机构θ的上限值越大，而广义凹肘节机构θ的下限值越小，且均趋近于arctan（H/L）。

为方便研究广义肘节机构位移增量放大系数随几何参数及侧移量变化的规律，需进一步将肘节机构几何参数限定在合理的参数取值域内，定义广义凸肘节机构几何参数与侧移量的参数取值域如下：L与L1的取值范围分别为0.4H≤L≤4H，0.2H≤L1≤L，θ的上限值由式（4）第一项限定，下限值为0˚，umax与u的取值范围分别为0.0018≤umax/H≤0.03 和u≤|umax|。针对广义凹肘节位移放大机构的参数取值域如下：umax与u的取值范围与广义凸肘节机构相同，θ取值上限值为80˚，θ取值下限由式（4）第二项限定，L与L1的取值范围分别为0.4H≤L≤3H与0.2H≤L1≤H。上述参数取值域的取值理由可归结为：首先，对于框架结构而言，在罕遇地震作用下规范规定的层间位移角限值为0.02，本文将umax/H取值范围限定在［0.0018，0.03］区间内，该区间在上述限值基础上进行了大范围的上探与下探，充分考虑了层间位移利用率的影响。其次，参数取值域对θ所作限定主要是因为经研究发现在该取值范围外进行θ取值时，肘节机构几乎不具备位移放大能力。最后，对于L与L1的取值域规定则几乎将现存所有肘节机构的研究应用案例均囊括其中，并做了大范围外扩。因而以上广义肘节机构的参数取值域实际上覆盖了绝大部分机构的可能选型，完全可以保证后续研究的普适性。

2 广义肘节机构性能评价与几何参数优化

广义肘节机构的功能为通过位移放大效应增加阻尼原件的耗能效率，因而最大化其位移放大能力是合理的优化目标。若某一个肘节机构在某侧移量区间内各点位移增量放大系数均大于另一肘节机构的结果，方能充分证明前者性能更优，可以此作为广义肘节机构位移放大性能的评价标准。为实现上述优化目标，首先研究当广义肘节位移放大机构的长度参数确定时，其位移增量放大系数随侧移量u与下连杆角度θ的变化规律。可通过对d求关于u与θ的偏导，在对应参数取值域内求解偏导数最小值，并根据其正负性判别规律，相关结果如表1所示。

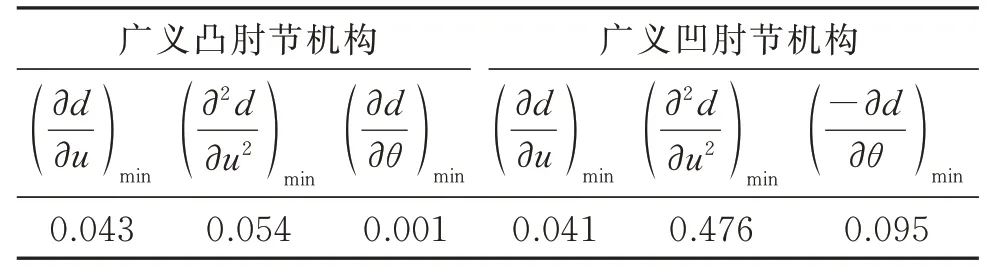
表1 位移增量放大系数最小偏导数值Tab.1 Minimum partial derivative values of displace⁃ment increment amplification factor

由表1可知，广义肘节机构的位移增量放大系数在机构几何参数确定时，为随u增大而单调递增的凹函数。且在H，L和L1确定时，其随θ趋近于arctan（H/L）而增大，但与此同时umax减小，因而对于长度参数固定的广义肘节机构，侧移量安全储备与位移放大能力是一对制衡量，对umax的合理估计是完成其机构几何参数优化的重要前提。因而针对长度参数固定的广义肘节机构，仅需将预先确定的H，L，L1和umax代入式（4），并直接以令式两端取等号的θ作为最优值，即可完成以最大化位移放大能力为目标的广义肘节机构下连杆角度优选。

为验证上述d随u与θ变化规律及优化方法的正确性，并以直观形式呈现fs，fq和d间的关系，对长度参数固定、umax=0.02H时的广义肘节机构进行分析，首先由式（4）合理确定θ的取值范围，并对比不同的θ取值时，［−0.02H，0.019H］侧移区间内上述放大系数。广义肘节机构各几何参数如表2所示，位移放大系数结果如图3所示。

表2 广义肘节机构几何参数Tab.2 Geometric parameters of generalized toggle mech⁃anism

图3 位移放大系数随θ 及u 的变化规律Fig.3 The variation law of displacement amplication factor with θ and u

图3中d随θ及u的变化规律与上文结论相一致，且随θ接近最佳取值，d（u）整体增大的同时时变效应会更加明显，广义肘节机构位移放大能力趋优。另外观察3 种广义肘节机构位移放大能力表征值随侧移量的变化趋势可知，位移放大系数小变形解无法反映位移放大能力的时变特性，位移全量放大系数因其平均属性并不直观和充分，而位移增量放大系数能够反映不同侧移量时肘节机构的位移放大能力，是一种物理意义更加明确的性能描述参数。

上文给出了当H，L，L1和umax确定后，以最大化位移放大能力为目标的θ选取方法，并证明了其合理性，这为在umax/H确定时比较各个长度参数配比下广义肘节机构的位移放大能力奠定了基础。然而通过穷举各长度参数配比的肘节机构，并依据d随侧移量的变化曲线幅值选取性能最优方案显然过于繁琐，因此亟需找到可以表征广义肘节机构位移放大能力的简化性能评价指标。

经研究发现，当umax/H确定时，以u=0 时的位移增量放大系数d（0）作为肘节机构的性能指标是合理的。为验证上述观点，在umax/H一定的情况下选取不同的H，L，L1配比方案并均使得θ取最优值，得到各方案的d（0），依据d（0）的幅值对各个配比方案进行排序，观测各方案在规定侧移区间内d（u）与d（0）大小关系的一致性。当umax为0.01H与0.02H时，对应的Δu（相邻两个取样点的间距）分别为0.002H与0.004H，则各方案d（u）与d（0）的结果如图4所示，图中等高线子图为较优构造方案的长度配比及对应d（0）。

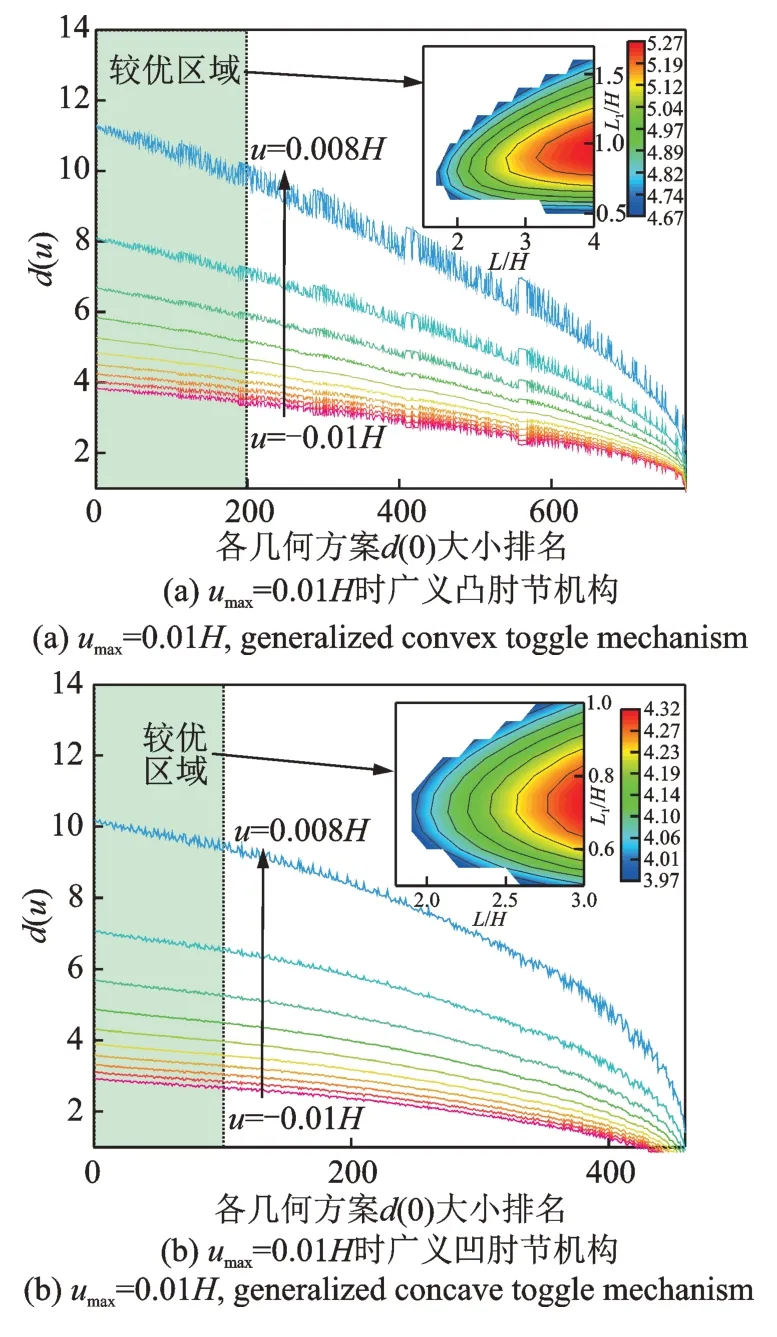
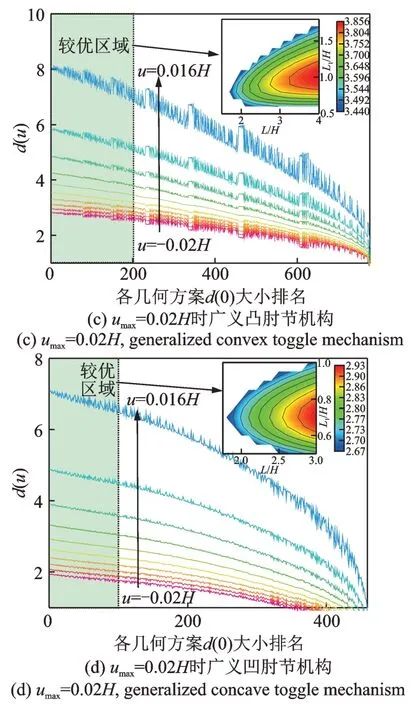
图4 耗能能力与d（0）大小的关系Fig.4 The relationship between energy dissipation capacity and d（0）

同时也可将不同umax方案按d（0）大小排序结果绘于同一图中，通过比较不同umax取值时d（u）的包络范围来直观表现正确选取umax对广义肘节位移放大机构几何参数优化的重要性，相关结果如图5所示，其中u的最小值取为−0.01H，u最大值取为0.009H。

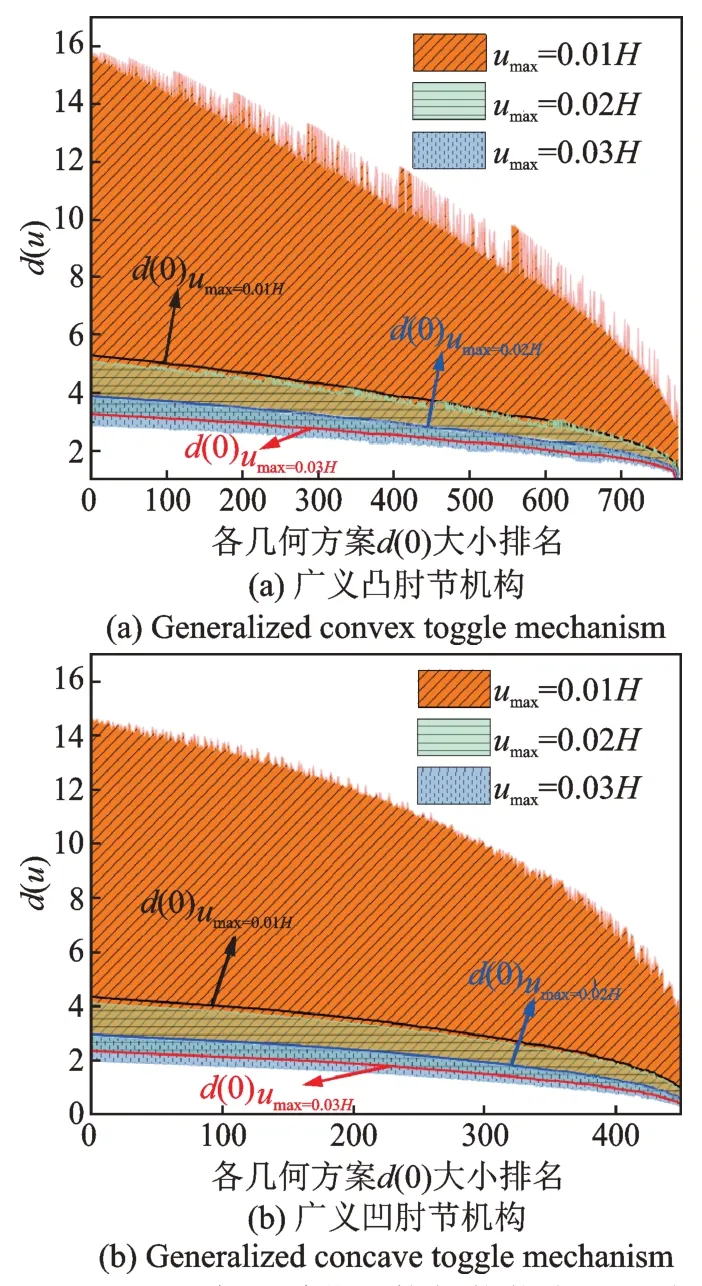
图5 umax对广义肘节机构耗能能力的影响Fig.5 The effect of umax on the energy dissipation capacity of generalized toggle mechanism

首先，由图4可知，在本文选取的广泛参数取值域内，umax/H相同的各个肘节方案中d（u）的大小关系与d（0）的大小关系具有较强一致性，这说明了以d（0）作为umax/H相同的广义肘节机构位移放大能力的评价指标具备合理性。其次，肘节机构位移放大能力越强，其增量位移放大系数的时变特性也愈明显。再次，根据等高线图结果可知：对于umax/H相同的各个几何配比方案，其d（0）随L/H增大而单调递增，结合计算分析可以证明对于广义肘节机构，其位移放大潜力会随L/H增大而增强。最后，针对umax/H不同的广义肘节机构，其较优的L1/H是较为固定的，对于广义凸肘节机构，其值随L增大而增大并趋近于1，对于广义凹肘节其值恒定在0.7 附近，可据此进行粗略的L1优选。

图5则说明了合理确定umax的重要性。当广义肘节机构umax/H不同时，直接依据d（0）大小比较其位移放大能力是错误的，这可能导致所设计肘节无法利用时变效应对位移放大能力的增益。因而对广义肘节机构的几何参数优化依赖于对其侧移量限值的准确预估，过大的估计umax会降低广义肘节机构的位移放大能力，反之则会降低机构侧移安全储备。

综上所述，以最大化位移放大能力为目标的广义肘节机构几何参数优化流程可归结如下：

（1）根据建筑结构形式与用户空间需求确定广义肘节形式，进行H，L选择，并根据减震控制目标合理确定umax取值。

（2）根据式（4）计算不同L1对应的最优θ，并将上述参数代入式（1）求解各方案所对应的d（0），最终以d（0）最大方案作为最优方案。

3 广义肘节机构的耗能特性及附加等效阻尼比计算

3.1 广义肘节机构的耗能特性及简化耗能计算参数

上文提出了位移增量放大系数概念且研究了其变化规律，并基于此给出了针对广义肘节机构位移放大能力的几何优化方法。以上述内容为基础阐明相关减震体系的耗能特性与耗能计算方法则可以进一步为结构减震设计提供理论支持。为深入分析广义肘节机构位移放大能力与耗能能力间的关系，构建如图6所示的单自由度体系。

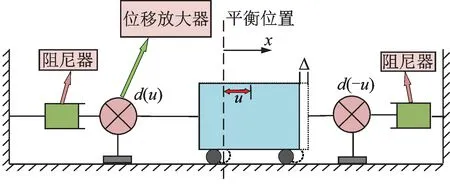
图6 对称布置广义肘节机构的单自由度体系Fig.6 Single-degree-of-freedom system of symmetrically arranged generalized toggle mechanism

该体系表示对称布置的两个广义肘节机构与结构串联，固结于地面的位移放大器代表广义肘节机构，其能够将结构相对于平衡位置的偏移放大并传递给阻尼器。规定位移放大器与结构间距增大时，位移增量放大系数增大。当结构由初始位置x=u移动极小位移Δ时，设该过程中阻尼器的耗能总量为W。由于Δ为微量，可视结构作匀速直线运动且位移增量放大系数保持不变，若阻尼器为黏滞阻尼器，且阻尼系数与速度指数分别为C与α，则W可由下式计算：

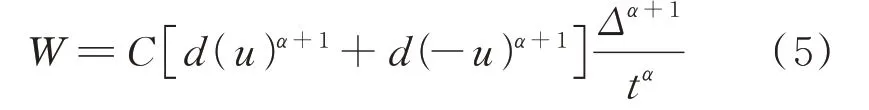
令g（u）=d（u）α+1，则g（u）的一阶导数为：

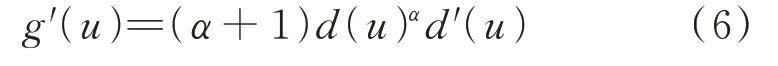
为比较不同侧移量时对称布置的广义肘节机构的耗能能力，令结构的初始位置分别位于x=u1和x=u2，且|u1|>|u2|，不妨设u1>u2>0，则由拉格朗日中值定理可知，（u2，u1）区间内一定存在u3，且（−u1，-u2）区间内一定存在u4使得以下关系成立：

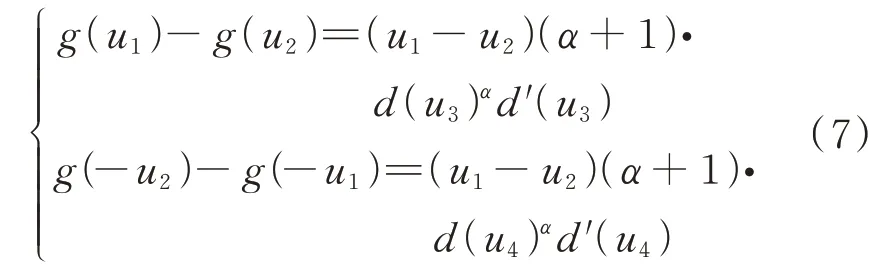
根据上文对于d（u）单调性与凹凸性的结论可知，式（7）中d（u3）>d（u4）且d′(u3)>d′(u4)，有下式成立：

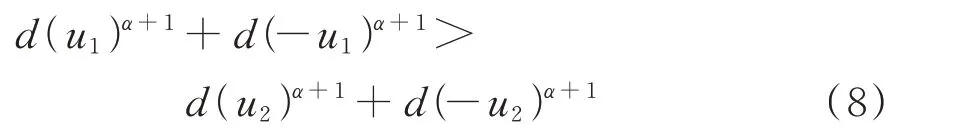
上式仅为预设u1，u2正负性的一种情况，但经分类分析后也可得到相同结论，即对于对称布置的广义肘节机构，理论上其侧移量越大则其耗能能力越强。采用金属屈服阻尼器与摩擦阻尼器作为肘节耗能元件时该性质同样适用，但受限于连杆刚度需求等原因，上述两种阻尼器在肘节式位移放大机构中应用较少，本文不展开讨论。因而结合上述证明可确定以d（0）作为对称布置的广义肘节机构的简化耗能计算参数是合理且保守的。另外，根据式（8）也可证明对于单侧布置的广义肘节机构，当其关于平衡位置做对称运动时，d（0）依然可作为其偏于保守的耗能计算参数。

故可结合应变能法建立结构自身属性、地震响应，以黏滞阻尼器作为耗能元件的广义肘节机构与等效附加阻尼比间的关系表达为以下形式：

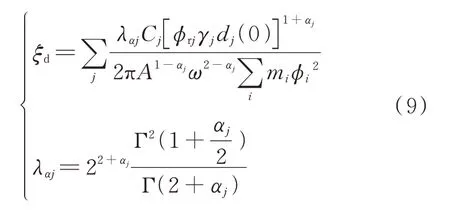
式中λαj为结构中第j个广义肘节机构中非线性黏滞阻尼器的折减系数，Cj为第j个广义肘节机构中黏滞阻尼器的阻尼系数，A为结构顶层最大位移，ϕrj为一阶振型下第j个肘节机构所在楼层层顶相对层底的水平模态位移，mi为第i层楼层质量，ϕi为第i层一阶振型下的归一化位移（顶层位移归一化为1），ω为一阶振型模态角速度。但应变能法本身推导过程中存在较多假设，加之广义肘节机构可能面临的层间位移利用率折减问题，式（9）仅可作为阻尼参数的初步估算式。

3.2 基于模态耗能的时变附加等效阻尼比计算方法

模态耗能法求解附加等效阻尼比概念清晰、结果准确，可指导减震方案中阻尼器的参数调整，从而实现精确控制阻尼比的效果。传统的模态耗能法作为一种时程平均无法考虑附加等效阻尼比随地震时程的演变，可在其理论基础上进行拓展，从而实现对于附加阻尼比时变特性的描述。单自由度体系在水平地震作用下的振动方程如下式所示：

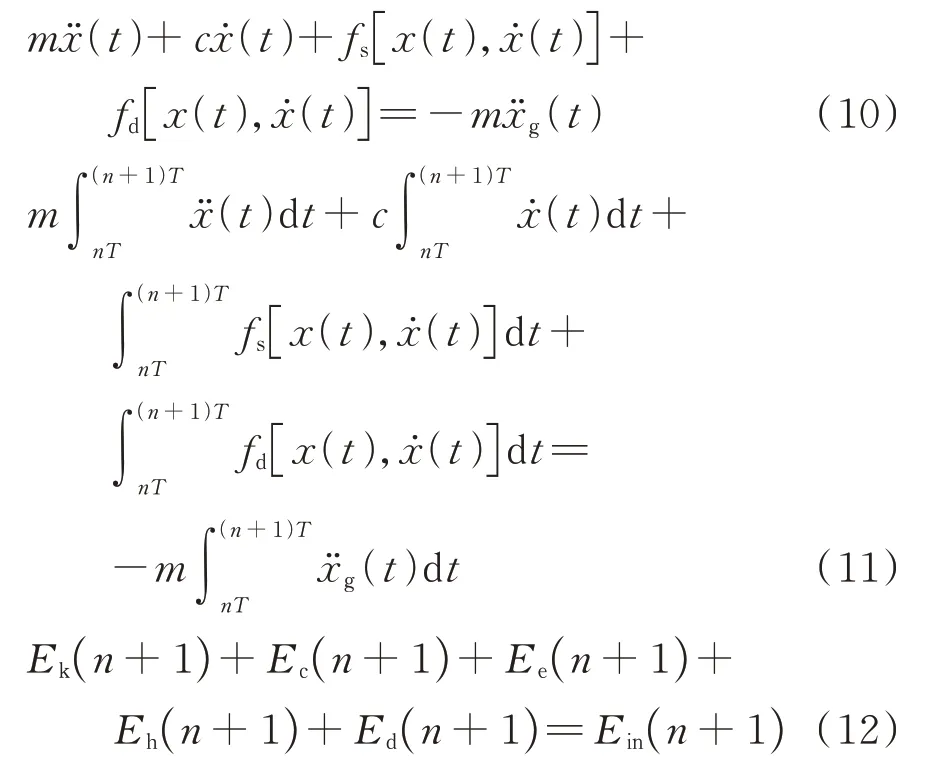
式（10）中，x（t），(t)和)分别为单自由度体系相对于地面的位移、速度和加速度为地面加速度；m，c分别为结构的质量及阻尼系数；fs[x(t)，(t)]为结构恢复力，fd[x(t)，(t)]为消能元件出力。对式（10）两端分别乘以(t)dt并在一定时间间隔内对两端求积分，同时设时间间隔为T，则可得到任一时间段内单自由度体系的相对能量方程，例如能量方程在第（n+1）个时间段［nT，（n+1）T］内有如式（11）形式，而其又可根据各项的物理意义写成式（12）形式。式（12）从左至右依次为第（n+1）个时间段内体系动能变化量、固有模态阻尼耗能量、弹性势能变化量、滞回耗能量、消能元件耗能量和输入体系能量。结构自身阻尼比可视为常数，而阻尼器所附加等效阻尼比可视为时间的函数，因而第（n+1）个时间段内消能元件附加等效阻尼比可用结构自身固有阻尼比、第（n+1）个时间段内阻尼器耗能量和结构固有阻尼耗能量加以表示，具体计算式如下：

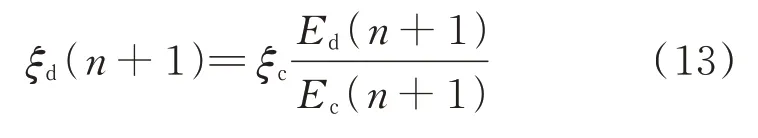
式中ξc表示结构自身阻尼比，ξd(n+1)表示阻尼元件于第（n+1）个时间段内附加等效阻尼比的时程平均值。该关系也可推广至多自由度体系，只需将Ed（n+1），Ec（n+1）与ξc分别做相应替换即可。另外由于结构在真实地震下很少呈现完整的滞回，且考虑到高阶振型周期的影响，T可以取为结构减震方向基本周期的1.0～1.8 倍。

显然时变阻尼比是一组时间序列数组，表征了结构耗能的演化特性。但为方便应用，可依据设计需求将其指定超越概率下的数值或数据均值作为代表值以表征附加等效阻尼比，显然当超越概率取值越高时，设计方案越保守和严格。本文以时变阻尼比数据均值作为附加等效阻尼比代表值指导减震方案设计。

4 广义肘节机构减震方案设计

上文已系统地阐明了以最大化位移放大能力为目标的广义肘节机构几何参数优化方法与以黏滞阻尼器为耗能元件的广义肘节机构附加等效阻尼比计算方法，据此可进一步提出广义肘节机构减震方案的优化设计方法。

现有消能减震结构设计方法的设防目标大多为确保结构层间位移角满足要求，但仅以此作为控制目标无法全面评价减震结构的耗能能力，在此基础上对多、罕遇地震作用下附加等效阻尼比进行控制，进而实现多级性能设防目标的减震设计则更为合理。有鉴于此，本文提出基于时变阻尼比与层间位移的面向多级性能设防目标的广义肘节位移放大机构减震方案设计方法，具体的设计步骤如下：

（1）对结构进行初步概念设计及传统抗震设计，基于结构抗震、减震需求及空间需求确定可布置广义肘节机构的位置，并根据可用空间确定各个广义肘节机构的H与L。若可利用空间平面接近矩形，则应采用广义凸肘节机构。若可利用空间平面接近三角形，宜采用广义凹肘节机构。并依据选取结果计算各层肘节层间位移利用率。

（2）对无控结构进行多条典型地震作用下弹塑性时程分析，提取各层最大层间位移并确定各层层间位移比例关系，将其写作归一化向量Φi，并近似认为受控结构第i层最大层间位移为UmaxΦi，其中Umax为罕遇地震作用下结构允许最大层间位移，随后根据目标安全余量st，i计算各层umax，i。广义肘节机构的实际安全余量定义为umax，i与罕遇地震作用下肘节所利用侧移最大值的差占其umax，i的比例，是衡量位移放大机构在罕遇地震作用下安全储备的指标，用si表示。引入安全余量的目的主要是为了考虑地震作用的强随机性并确保所设计减震方案在罕遇地震作用下可以稳定发挥作用，umax，i的初始值可设为γiUmaxΦi（1+st，i）。

（3）根据H，L和umax，i，采用本文前述方法对各个广义肘节机构进行几何参数优化。

（4）根据多遇地震作用下目标附加等效阻尼比，进行弹性反应谱分析得到结构顶部最大位移并提取结构一阶模态振型侧移曲线，据此通过式（9）初步确定广义肘节机构中黏滞阻尼器阻尼参数。

（5）对减震结构进行多遇地震作用下弹塑性时程分析，判断层间位移角及时变阻尼比均值是否满足控制目标，若未达目标，则调整阻尼参数，直至两者均满足目标。在罕遇地震作用下也采用该方法进行阻尼参数调整。

（6）检验各层广义肘节机构安全余量是否满足要求，即si是否大于st，i。若安全余量不满足要求可采取两种方法进行设计方案调整：当安全余量与目标值差距较大时，应增大对应层广义肘节位移放大机构umax，i，即对步骤（2）中umax，i的估计值进行修正，并返回步骤（3）进行几何参数再优化；若安全余量与设定值较为接近，则可通过微调阻尼参数并重新进行罕遇地震作用下时程分析。若各层广义肘节机构安全余量均符合要求则设计完成。

上述设计步骤可概括为图7所示流程图。

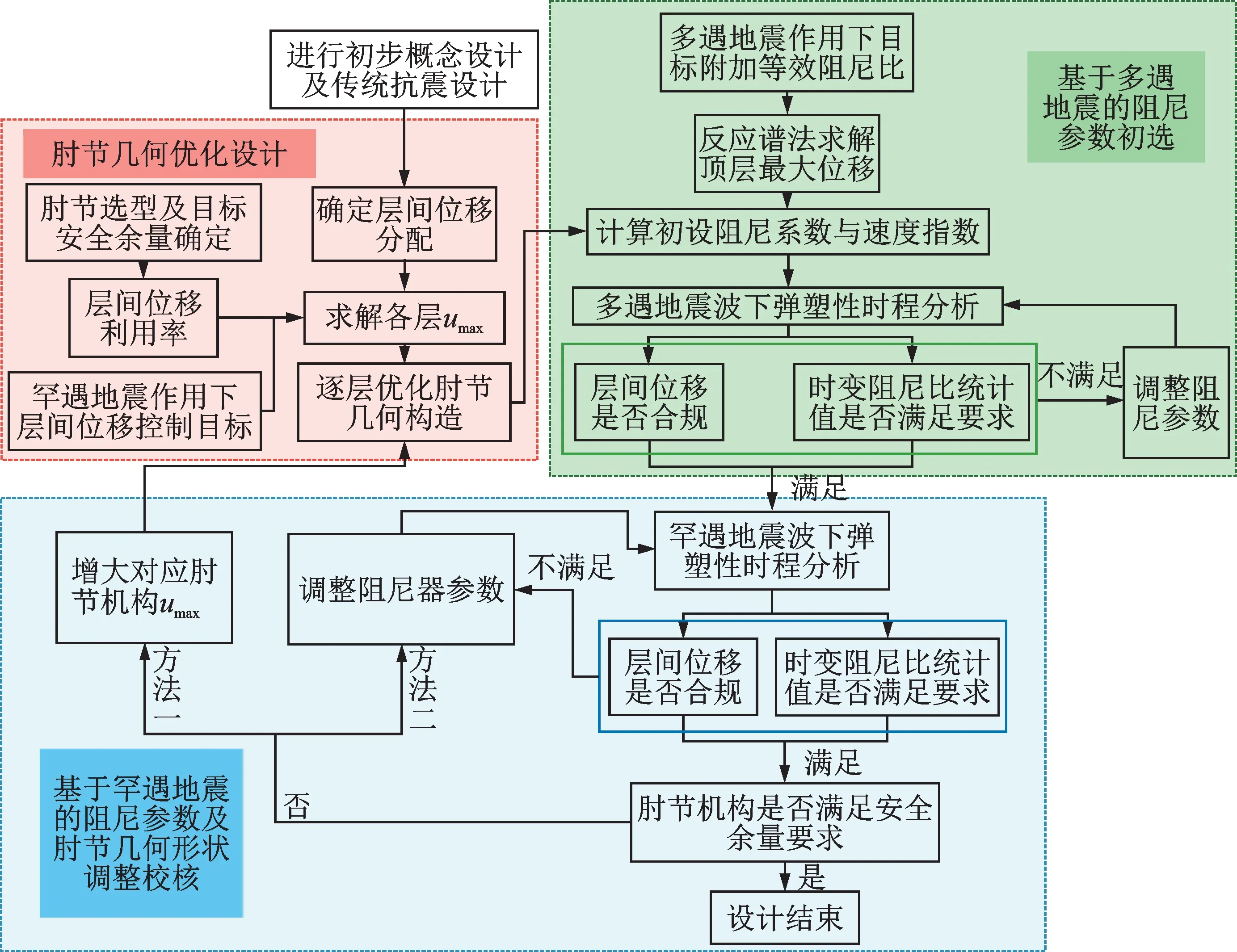
图7 设计流程图Fig.7 Design flow chart

该设计流程在广义肘节机构几何参数优化方面兼顾了其大震作用下的安全性及位移放大效率，面向多性能目标的阻尼参数选取方法普适于以黏滞阻尼器作为耗能元件的各种布置形式。

5 算例分析

为验证面向多性能目标的广义肘节机构优化设计方法的有效性，选取一个9 层的半刚性钢框架进行减震设计及分析。钢框架所在地设防烈度为8 度（0.3g），场地特征周期为0.55 s，结构自身阻尼比为0.02，结构尺寸与各层质量如图8所示。框架柱构件采用热轧H 型钢（截面高度×截面宽度×腹板厚度×翼缘厚度）400 mm×400 mm×45 mm×70 mm，梁构件采用热轧H 型钢800 mm×300 mm×14 mm×22 mm，对于梁柱的弹塑性变形可以通过塑性铰单元模拟，梁柱连接节点的半刚性连接由非线性连接单元模拟，非线性连接单元采用Kinamatic 滞回类型。结构自振周期为1.93 s，肘节连杆与阻尼器支撑均设为刚体。层间位移减震目标为：多遇地震作用下层间位移角限值为1/300，罕遇地震作用下层间位移角限值为1/60，因而罕遇地震层间允许最大位移Umax=66 mm。多遇和罕遇地震下阻尼器附加等效阻尼比目标分别为13%和7%。减震方案分别采用传统凹肘节方案、广义凸肘节方案和对角斜撑方案，规定各层肘节目标安全余量至少为10%，阻尼元件均采用非线性黏滞阻尼器，且为方便地对比各方案阻尼系数用以区分不同方案减震效率，速度指数统一选择为0.5。传统凹肘节机构L取为7.2 m，而对于广义肘节机构，为将其布置灵活、节省空间的优势加以展现，并兼顾较强的位移放大能力，本文广义肘节方案中机构的H与L分别选为1.8 m 和7.2 m。本文选用3 条天然地震波对结构减震方案进行设计，所选地震波信息如表3所示，所选地震波的平均反应谱与目标反应谱关系如图9所示。

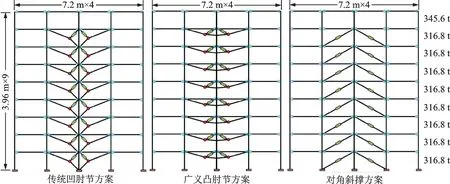
图8 三种减震布置方案Fig.8 Three types of damping arrangements

图9 目标反应谱和选取地震波的平均反应谱Fig.9 Target response spectrum and average response spectrum of selected seismic waves

表3 设计所用地震波Tab.3 Seismic waves used in design

根据无控结构模态分析结果与在上述地震波作用下结构响应结果可得如表4所示肘节优化所需参数。根据表4及前述预设参数可进行各层肘节机构几何参数优化，优化步骤可概括为：首先根据umax与H，L长度选取不同长度L1，并将长度参数结果代入式（4），求解各长度方案的最佳θ；随后令u=0，并将对应几何参数代入式（1）以计算d（0），选取d（0）最大的方案作为最佳几何构造。以结构中1 层、7 层、8层的传统肘节机构及广义肘节机构为例演示最优L1选取过程，结果如图10所示。

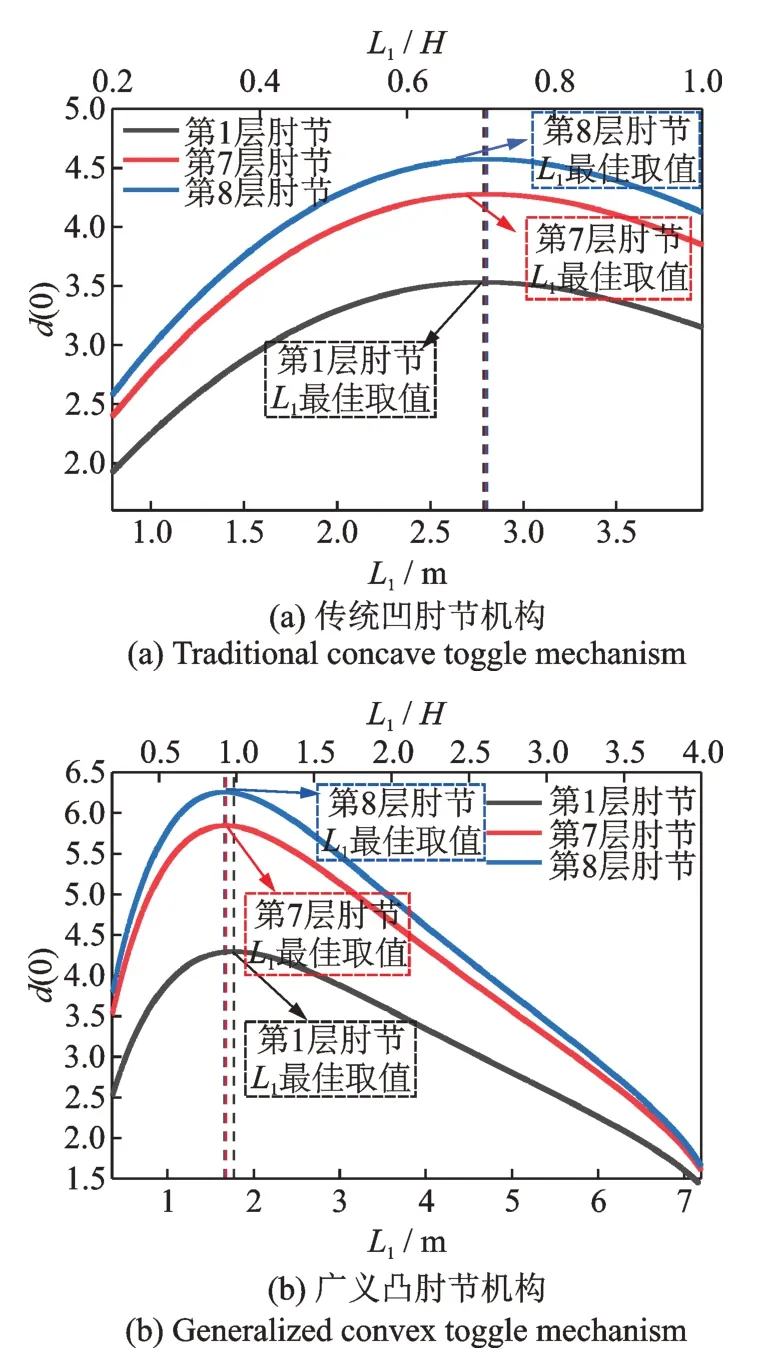
图10 减震方案L1长度优选Fig.10 Optimal length of L1 in vibration reduction scheme

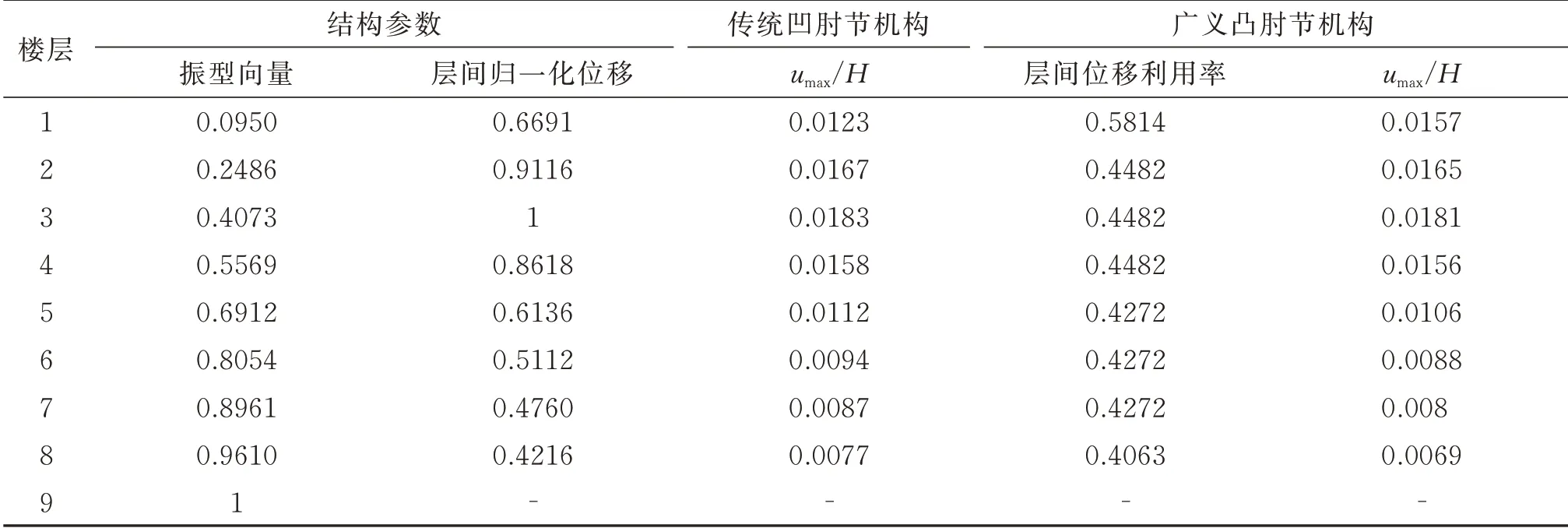
表4 肘节几何参数初步优化所需参数Tab.4 Parameters required for preliminary geometry optimization of toggle mechanism

在完成初步几何参数优化后，根据目标附加等效阻尼比、结构各层质量、一阶振型信息、层间位移利用率数据、各层肘节d（0）依照式（9）进行阻尼器参数初选，随后根据层间位移响应时程、时变阻尼比结果及各层肘节安全余量结果作为判据迭代调整肘节中阻尼器参数或修正各层肘节侧移限值，直至调整至上述3 个参数均满足控制目标，迭代过程限于篇幅在此省略。经初步优化得到肘节几何参数结果及最终肘节几何参数结果如表5和6 所示。由以上结果可知，虽然各层肘节机构umax/H并不相同，但最优L1长度与H的比值相对固定，传统凹肘节机构的L1/H的最优值在0.7 附近，广义凸肘节机构L1/H的最优值在1 附近，这与前文结论一致。各减震方案中黏滞阻尼器阻尼参数取值、阻尼器在上述地震波作用下阻尼器最大出力及安全余量结果如表7所示。

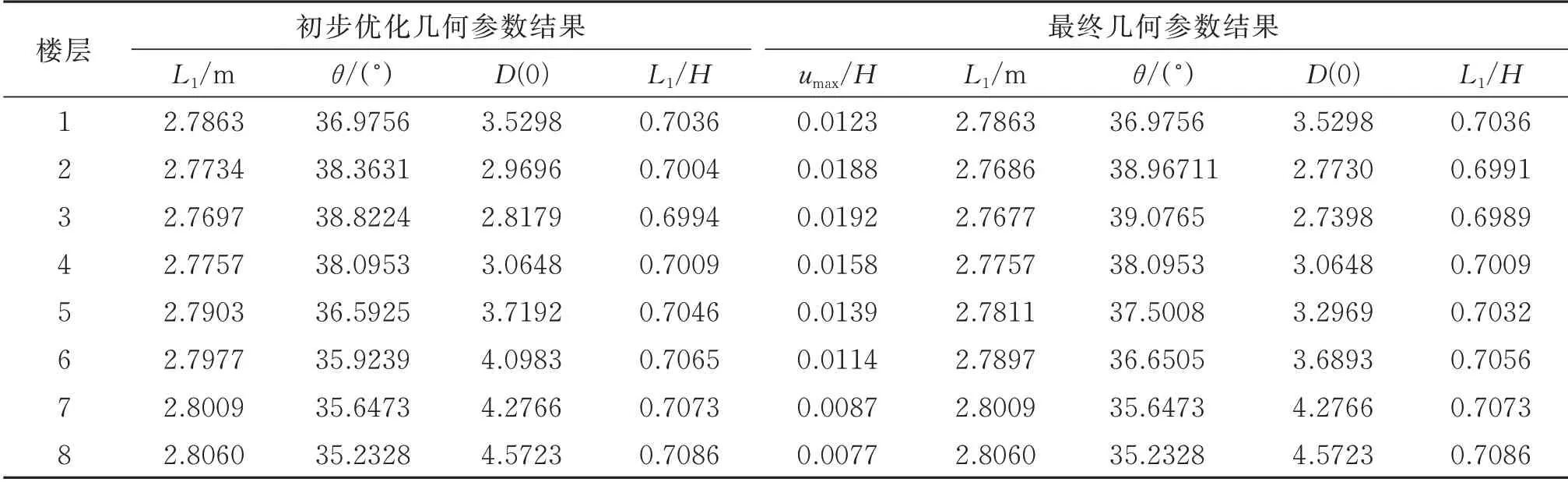
表5 传统凹肘节方案几何参数优化结果Tab.5 Geometric parameter optimization results of traditional concave toggle schemes

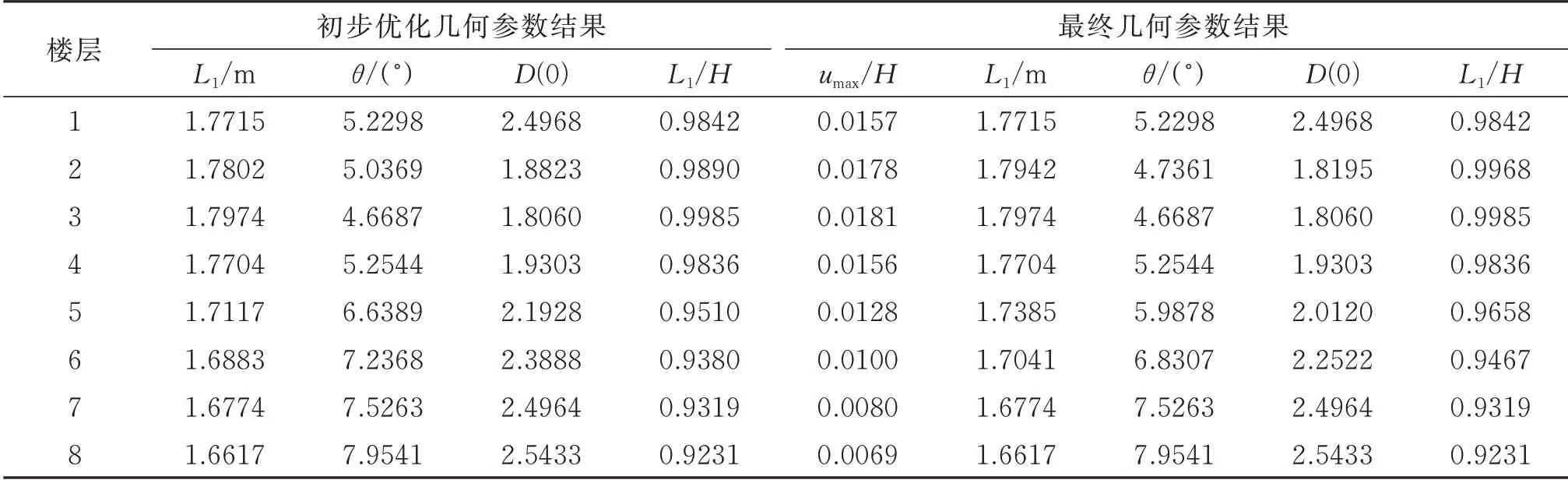
表6 广义凸肘节方案几何参数优化结果Tab.6 Geometric parameter optimization results for generalized convex toggle scheme

由表7可知，首先各层肘节机构在安全余量指标上均满足设计目标，这使得肘节机构在具有强随机性的地震作用下具有一定安全储备。另外在3 种最终减震方案中所采用黏滞阻尼器的阻尼系数及最大出力存在明显差异，两种肘节式布置方案因层间位移放大作用而使得黏滞阻尼器具有更高的耗能效率，阻尼器的阻尼系数需求及吨位需求均小于对角斜撑布置方案，黏滞阻尼器的成本相对较低。其中广义凸肘节布置方案因层间位移利用率较小因而在阻尼系数与吨位需求上大于传统凹肘节布置方案，但其在布置灵活性及空间节约性方面都更具优势。各减震方案的层间位移角结果、顶部位移及加速度时程结果与时变阻尼比结果如图11～13 及表8所示。

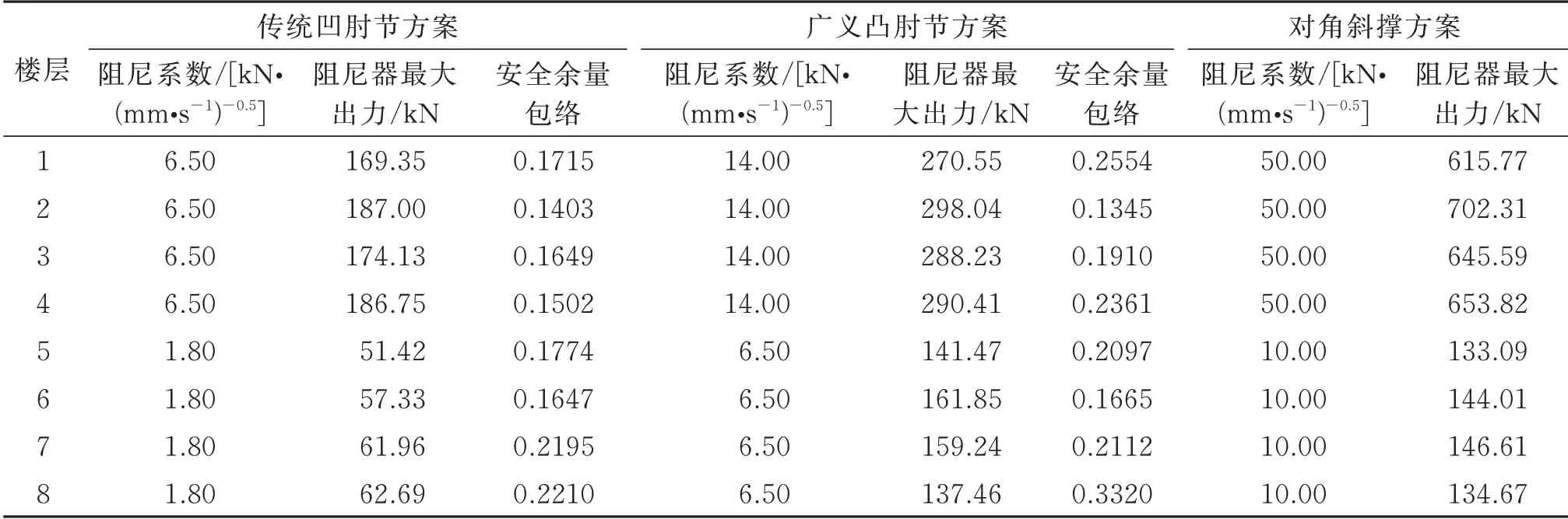
表7 阻尼系数取值、最大出力及安全余量结果Tab.7 Damping coefficient value，maximum output and safety margin results

表8 时变阻尼比均值结果Tab.8 Time⁃varying damping ratio average results

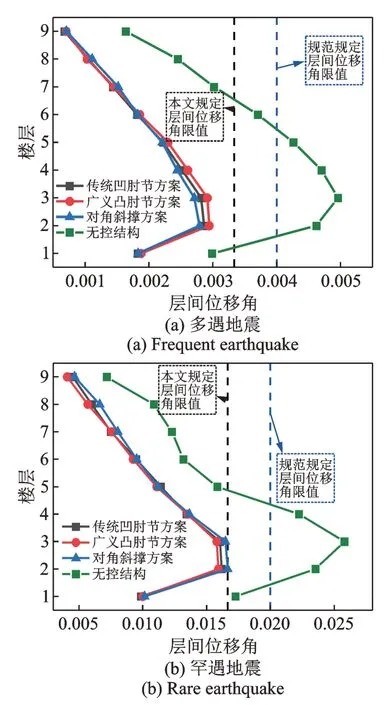
图11 层间位移角最大包络Fig.11 Maximum envelope of story drift ratio

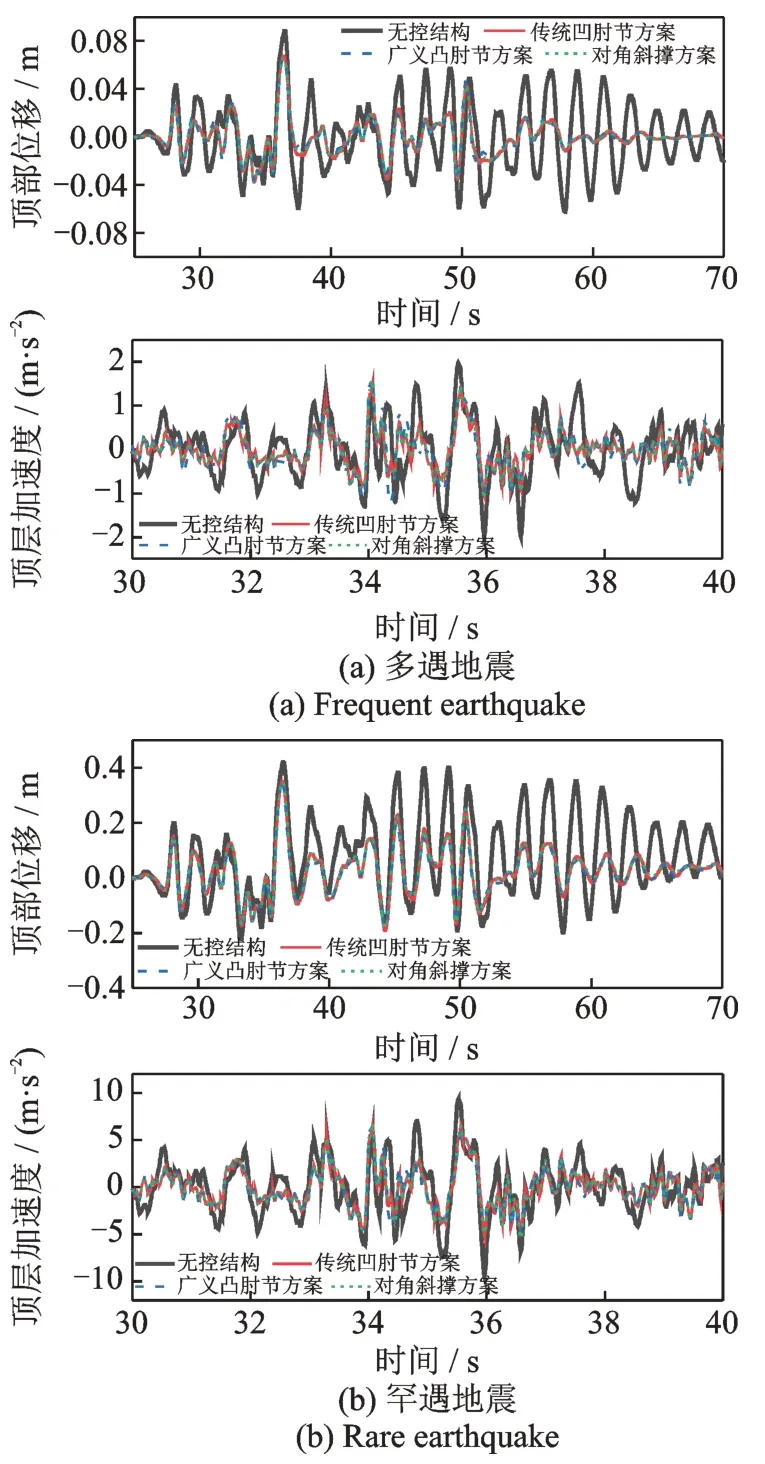
图12 RSN-1489 波作用下结构顶部位移及加速度时程Fig.12 Time history of displacement and acceleration at thetop of structure under the action of RSN-1489 wave

由层间位移及附加等效阻尼比结果可知按本文方法设计的3 种减震方案均满足目标要求。由阻尼比结果可知：对于3 种减震方案，罕遇地震作用下附加等效阻尼比相比多遇地震下的结果有一定衰减，其中广义凸肘节方案衰减最少，而对角斜撑方案衰减最多。附加等效阻尼比的衰减可归因于所使用阻尼器速度指数较小，这致使阻尼器在罕遇地震作用下出力不能线性增长，从而造成阻尼器周期耗能量的增幅相较于周期模态耗能的增幅偏小，该现象直观反映于图13的能量累积图中。至于肘节方案附加等效阻尼比衰减较小的现象可归因于对称布置的肘节机构的耗能能力会随侧移量增大而增强。两种肘节方案间阻尼比衰减量的差异则是因为当umax/H相近时，广义凸肘节机构具有比传统凹肘节机构更明显的时变效应，具有更大的耗能能力增幅。

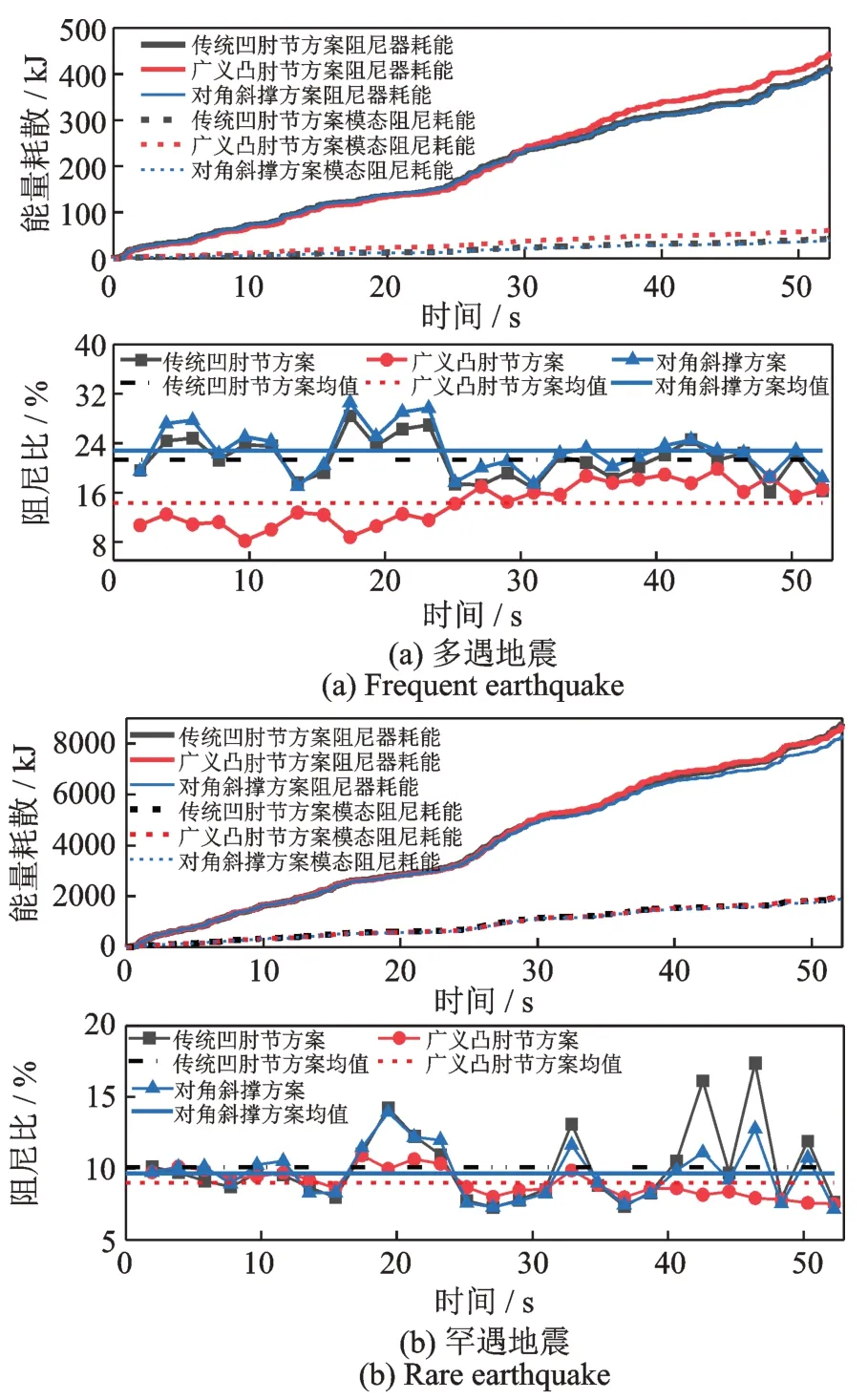
图13 RSN-169 波作用下耗能累积量与时变阻尼比Fig.13 Cumulative energy consumption and time-varying damping ratio under RSN-169 wave

综上，肘节减震方案的主要优势为：肘节机构通过将结构层间位移放大并加载至黏滞阻尼器两端，从而增大了其变形，进而增强了阻尼器的耗能效率，降低了阻尼器对吨位的需求，可显著降低减震方案成本。另外由于肘节机构增量位移放大系数的时变特性，对称布置的肘节机构的耗能能力会随肘节侧移量变大而增强，该增益效果是传统的阻尼器布置形式（对角斜撑式布置、人字支撑式布置等）所不具备的，因而理论上肘节方案的减震效果在大震下更具优势。

但需要指出的是，由于广义凸肘节的构造及出力方式，在地震作用下梁、柱局部可能由于上、下连杆轴力的作用而出现较强的附加剪力，本文广义凸肘节方案对应减震结构在三条地震波作用下各楼层的中柱所受最大剪力的均值结果如图14所示。

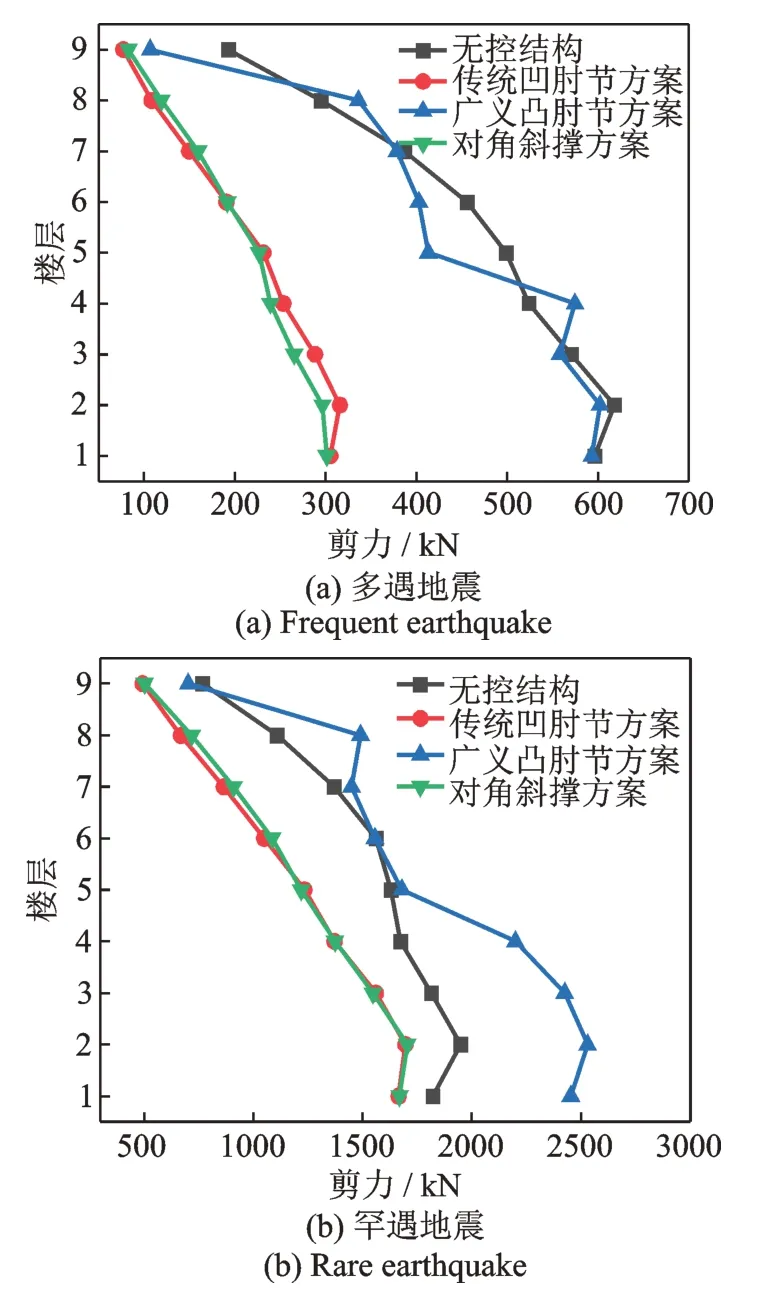
图14 结构中柱最大剪力均值Fig.14 Mean of maximum shear force of column in structure

上述结果表明广义凸肘节方案中部分楼层的中柱所受剪力甚至可能大于无控结构的中柱所受最大剪力，但考虑到减震结构的层间位移已得到有效控制且剪力增幅可以接受，因此方案仍然是安全可靠的。在进行广义肘节减震方案设计时，应对相关柱的抗剪承载力及稳定性进行严格验算，必要时可通过提高配筋率或增大柱截面面积等手段避免剪切破坏与失稳出现。

综上所述，本文提出的设计方法可保证肘节机构的安全性与高效性，并广泛适用于各种以黏滞阻尼器作为耗能元件的减震方案设计。另外，广义肘节机构兼顾了耗能高效性与空间节约性，且由于其自身形式的灵活性，不仅可单独使用，也可与传统肘节等其他形式的消能装置共同使用，具有广泛的应用前景。

6 结 论

针对传统肘节机构占用空间较大的缺点及目前研究中对肘节机构位移放大能力概念认识的不足。本文拓展了传统肘节机构的形式，提出了布置灵活、占用空间小的广义肘节机构。建立了以最大化位移放大能力为目标的广义肘节机构几何优化方法，分析了广义肘节机构位移放大能力与耗能能力的关系，得到了广义肘节机构的耗能简化计算参数，最后基于应变能法附加等效阻尼比计算方法与模态耗能时变阻尼比计算方法，给出了面向多性能目标的广义肘节减震方案设计方法。本文主要结论如下：

（1）位移增量放大系数d可准确描述不同侧移量时广义肘节机构的位移放大能力，其物理意义明确，相较于位移全量放大系数与位移放大系数常数小变形解可更好地描述广义肘节机构性能。

（2）对于umax/H相同的广义肘节机构，d（0）是合理的性能评价指标，可直接以d（0）大小比较同类肘节机构的位移放大能力。

（3）合理预估umax值对于广义肘节机构几何参数优化至关重要，高估umax会降低广义肘节机构的位移放大能力，低估umax会增加广义肘节机构的失效风险。

（4）广义肘节机构最优L1/H值随umax/H变化很小，对于广义凸肘节机构该值会随L增大而增大，最终稳定在1 附近，而对于广义凹肘节该值恒定在0.7附近。

（5）广义肘节机构随L/H的值增大其位移放大潜力会相应增强。

（6）对称布置的广义肘节机构其位移放大能力与耗能能力均会随侧移量增大而增强，可采用d（0）作为其偏于保守的简易耗能计算参数。

（7）本文提出的减震方案设计方法可兼顾广义肘节位移放大机构的安全与效率，是一种行之有效的设计方法。

（8）广义肘节机构相联柱在地震作用下承受剪力较大，在结构设计时应加以注意，并在设计完成后进行抗剪承载力及动力稳定性验算。