对称锥非线性互补问题的无穷范数宽邻域算法

赵花丽

(咸阳师范学院数学与统计学院，陕西 咸阳 712000)

0 引言

内点算法是求解对称锥互补问题的一类非常有效的方法，当今关于对称锥非线性互补问题的研究还处于不成熟阶段，相关的研究较少.2006年,Yoshise[1]扩展了Andersen等[2]提出的齐次模型,随后基于该模型提出了单调对称锥非线性互补问题的齐次算法[3].Zhao等[4]在新的SLC条件下估计了单调对称锥非线性互补问题的齐次算法的理论复杂度.笛卡尔P*(κ)对称锥非线性互补问题是一类非单调非线性互补问题，单调问题是该问题的特例，因此研究笛卡尔P*(κ)对称锥非线性互补问题就成为研究的热点，Zhao等[5-7]对不可行内点算法做了相关的研究.

一直以来，学者们都在研究如何改进宽邻域算法的理论复杂度.2005年，Ai等[8]定义了一个Frobenius范数宽邻域,得到了和窄邻域短步算法具有相同复杂性的宽邻域算法.随后该邻域被推广到半定规划和对称锥优化问题中[9-10].然而上述研究都是基于可行算法的，Liu等[11]将Ai等的邻域进行了简化,给出了宽邻域不可行内点算法并获得了较好的理论复杂度.随后,Yang等[12]将不等式中的Frobenius范数换成1范数,并且利用该邻域得到了较好的算法.2018年，Asadi等[13]进一步得到无穷范数宽邻域，分析了笛卡尔P*(κ)线性互补问题的内点算法的复杂度.本文基于Asadi等提出的无穷范数宽邻域,给出了笛卡尔P*(κ)对称锥非线性互补问题一个无穷范数宽邻域不可行内点算法.

1 欧几里得若当代数与对称锥

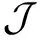
ⅰ)x∘y=y∘x；

ⅱ)x∘(x2∘y)=x2∘(y∘x),其中x2=x∘x；

ⅲ)〈x∘y,z〉=〈x,y∘z〉,其中x∘y为x和y的若当积.

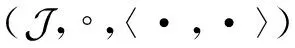
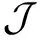
关于对称锥更为详细的介绍,请参考文献[14].

2 算法及预备知识

其中

I+={v:〈x(v)-y(v),φ(x)(v)-φ(y)(v)〉≥0}，I-={v:〈x(v)-y(v),φ(x)(v)-φ(y)(v)〉<0}.

本文假定严格可行集非空.考虑迭代点在以下宽邻域的情形：

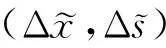
(1)

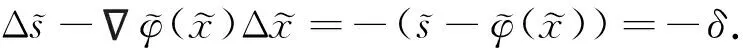
(2)

给定步长α∈[0,1],则新的迭代为

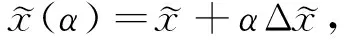
(3)

(4)

这里α满足:

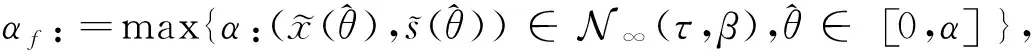
(5)

(6)

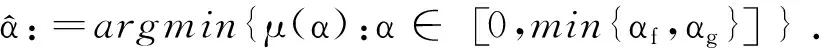
(7)

算法1(不可行宽邻域内点算法)

[步骤1] 如果μk≤ε,则停止.

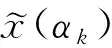
[步骤4] 令(xk+1,sk+1)=(x(αk),s(αk)),计算新的对偶间隙μk+1=〈xk+1,sk+1〉/n.令k:=k+1， 转步骤1.

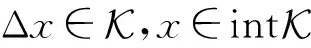
3 复杂度分析

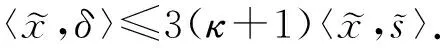
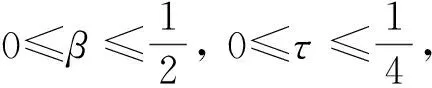
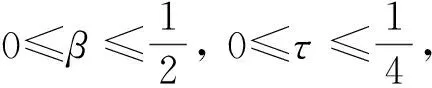
证明ⅰ)由引理1有

ⅱ)利用引理2和引理3有

所以ⅱ)成立.

ⅲ)由于

故成立.

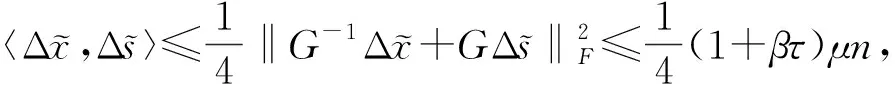
因此ⅳ)成立.

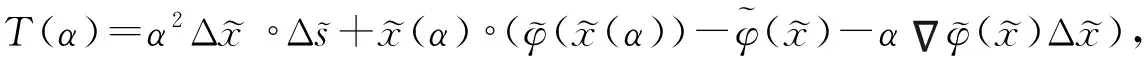
又由引理3,可知

令

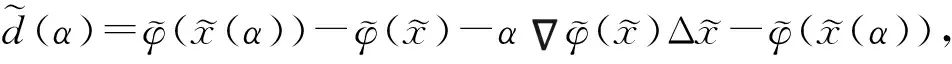
所以有

所以

ⅰ)μ(α)≤(1+α(τ-1+τβ)+Cα2n3/2)μ；

ⅱ)μ(α)≥(1+α(τ-1)-Cα2n3/2)μ.

证明ⅰ)经过简单计算可知

因为

所以有μ(α)≤(1+α(τ-1+τβ)+Cα2n3/2)μ.

ⅱ)因为

tr(h(α))≥nμ+α(τ-1)nμ=(1+α(τ-1))nμ，

所以μ(α)≥(1+α(τ-1)-Cα2n3/2)μ.

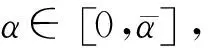
因此由引理5、引理6和引理7有

‖(τμ(α)e-h(α))+‖∞+‖(T(α))-‖∞≤

‖(τμ(α)e-h(α))+‖∞+‖T(α)‖∞≤βτμ(α),

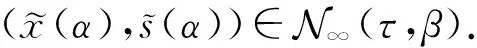
证明由引理8,可知

证明由引理8,有

μ(α)≤μ+α(τ-1+βτ)μ+Cα2μn3/2≤μ[1-(1-τ-βτ-Cαn3/2)α]≤

利用引理11,可获得下面的复杂度.

推论1当使用NT方向时,算法1至多O((2+κ)3n9/4logε-1)步终止.当使用xs方向时,算法1至多O((2+κ)3n4logε-1)步终止.当使用sx方向时,算法1至多O((2+κ)3n5/2logε-1)步终止.

4 数值实验

以下测试算法1的实际计算效果.在算法的执行中,取参数γ=0.000 1.算法的终止条件为max{r,mu}≤1e-6.可行性残差r=‖s-φ(x)‖F,互补间隙mu=〈x,s〉/n，k表示算法的迭代步数，t表示算法的运行时间.

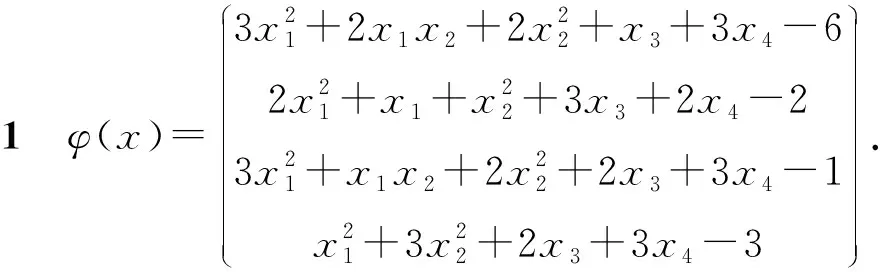
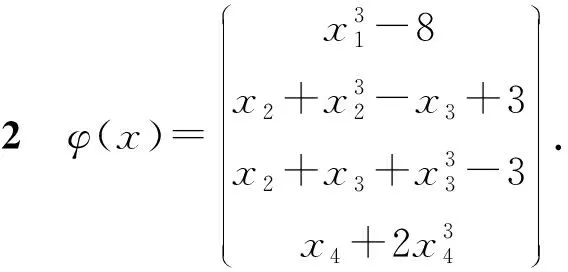
在这里，分别对n=500,n=1 000,n=1 500,n=2 000进行计算，结果列于表1.

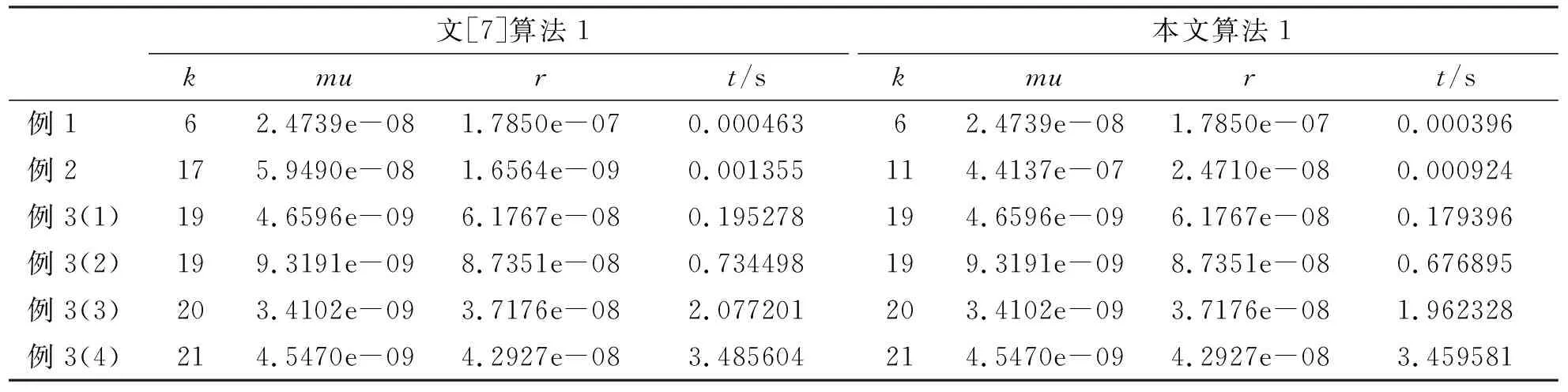
表1 非线性互补问题的数值结果Tab.1 The numerical results for nonlinear complementarity problems

从表1数据结果来看，本文提出的算法1与文献[7]中的算法1迭代步数基本相同，但是计算时间优于文[7]中算法1.