双层微金字塔结构耦合空间光调制的光子纳米射流研究
2022-02-15孙泽华刘卫国葛少博刘丙才吴春芳惠迎雪
孙泽华,刘卫国,葛少博,刘丙才,吴春芳,惠迎雪
(西安工业大学 光电工程学院 陕西省薄膜技术与光学检测重点实验室,西安 710021)
0 引言
当平面波照射介电材料微结构时,会在阴影面出现高强度能量聚集区域并向远场辐射,这就是光子纳米射流(Photonic Nanojet,PNJ)效应[1]。得益于PNJ 横向光场的高度空间局部化,可以将倏逝场向传播场转化,进而突破衍射极限,并且能在一定距离上保持近无衍射地传播。同时,PNJ 易与其他技术集成的属性也使其在超分辨成像、生化分析检测和超高密度光存储等各个领域展现出了巨大的应用价值[2]。
自2004 年CHEN Zhigang 等提出光子纳米射流的概念以来,研究人员通过改变各种参数探寻影响光子纳米射流性能特征的因素[3]。结果表明,光子纳米射流的形成与微结构形状、入射波长和微结构与背景折射率之比(即折射率对比度)等参数有关[4]。其中,折射率对比度的改变可以显著影响光子纳米射流的光场分布。例如,在波长为800 nm 时,对直径5 μm 的单粒子进行近场光场的建模,粒子处于水介质中比在空气中产生光子纳米射流的焦距增加了2λ[5]。此外,立足于微结构本身折射率的改变也是一种常用思路,例如,波长为400 nm,微球直径同为2 μm 的情况下不同结构产生的光子纳米射流,当微球为折射率1.59 的聚苯乙烯时,聚焦光场的纵向长度为4.7λ;当微球为折射率由1 到2 的100 层等厚同心壳梯度时,聚焦光场的纵向长度增加到11.8λ[6]。相关研究虽然能获取不同的光子纳米射流,但无法实现动态调控,而液晶凭借着外场可调的特性走入了学者们的视野。MATSUI T 等将液晶引入光子纳米射流领域,数值计算结果表明不同程度双折射的微圆柱可以调制光子纳米射流的焦点位置,为后续研究提供了更多的可能性[7]。随后,与液晶组合改变折射率对比度进而实现可调光子纳米射流的方式被接连提出[8-9]。如,将液晶分散到聚合物中形成自组装液晶微滴,在532 nm 的激光照射下产生的光子纳米射流在加电压后焦点横向宽度增加了0.38λ[10]。杜斌涛等将微球、双层微球浸入液晶改变背景折射率实现了光子纳米射流的开关,焦距最大达到17.5λ,聚焦光场的纵向长度最高可达26.25λ[11]。综上所述,液晶作为典型的空间光调制手段可以赋予光子纳米射流动态调控的特性,将液晶与微纳结构相结合,展现出低电压控制、低制备成本和灵活的外场调制等优点,在精密细胞手术的光学手术刀和纳米物体操作的光钳等场合具有巨大的应用潜力[12]。但是已有的液晶PNJ 大多围绕微球结构开展,当考虑到液晶结合异质材料梯度轮廓的微结构时,其光场可调谐特性值得进一步研究。
本文提出了一种双层微金字塔结构耦合空间光调制的光子纳米射流光学元件,将液晶引入到双层微金字塔阵列结构中,以具有导电能力的氧化铟锡(Indium Tin Oxide,ITO)作为上下电极,施加电压使液晶分子发生偏转,改变液晶折射率从而调节微结构与背景折射率之比,实现光子纳米射流聚焦光场的可调谐。利用时域有限差分方法(Finite Difference Time Domain,FDTD)改变液晶分子旋转角进行模拟仿真,分析了微结构背景折射率改变时,光子纳米射流的光场强度、衰减长度和半高全宽的变化规律。
1 理论与仿真设计
1.1 理论
液晶是一种介于液态和固态晶体温度区间内的物质相态,由具有有序性和电光各向异性的纳米级细长棒状有机分子组成[13]。液晶的结构决定了其具有可调谐、光、电、磁等独特的性质,外部因素如电场、磁场、光和温度等微小变化就会使液晶分子的排列结构发生改变,从而实现不同的功能[14]。液晶相态一般可分为三种,近晶向、胆甾向及向列相,其中向列相液晶具有单轴晶体的光学性质,对外界作用非常敏感,其分子排列基本沿着同一个方向,粘度小、流动性强,应用最为广泛[15]。向列液晶5CB 的液晶态范围为22~35 ℃,能够在常温条件下应用,本文中的液晶材料选用向列液晶5CB[16]。
FDTD 仿真软件中液晶分子在外部机制下沿xyz各平面的取向如图1,θ为液晶分子在xy平面的投影与x轴的夹角;φ为液晶分子在yz平面的投影与y轴的夹角,改变θ、φ的角度以模拟对液晶施加电压使液晶分子偏转从而改变液晶折射率。由于电场方向沿z轴,且在实验中有配向层约束液晶分子的排列,设置θ=90°,只考虑φ值变化。液晶为具有寻常光折射率no和非常光折射率ne的各向异性材料,对于向列液晶5CB,no=1.52,ne=1.67。液晶的有效折射率可表示为


图1 液晶分子在外部机制下沿xyz 各平面取向示意Fig.1 Schematic of liquid crystal molecules orientation along xyz planes under an external power
1.2 仿真设计
搭建的模型是在双层微金字塔结构阵列中加入液晶从而实现光子纳米射流的可调谐,液晶层采用向列液晶5CB;氧化铟锡作为施加电压的电极分别放置在微结构的底端与顶端,结构如图2,基底与微结构的总高度为6.5 μm。金字塔上层结构是折射率n1=1.45 的石英玻璃,高h2=1.3 μm,长与宽均为L2=3.8 μm;金字塔下层结构为折射率n2=1.99 的Si3N4,高h1=2 μm,长与宽均为L1=7.6 μm;下层基板为长10 μm、宽10 μm、高3 μm 的玻璃材质;上下ITO 极板的长和宽均为10 μm,高h3=0.1 μm。设置入射平面波波长λ=960 nm,网格精度为波长的1/10,x、y轴的仿真条件为周期性边界条件,z轴方向上为PML 边界条件终止计算空间并吸收反射波。
如图2,衡量光子纳米射流性能特征的参数主要有焦点位置、纵向长度、焦点处横向尺寸和光强。微结构表面到焦点的距离为焦距f;微结构表面到光子纳米射流末尾的纵向长度为衰减长度L;w为焦点横向尺寸,一般由焦点光强分布的半高全宽(Full Width at Half Maximum,FWHM)定义[17]。
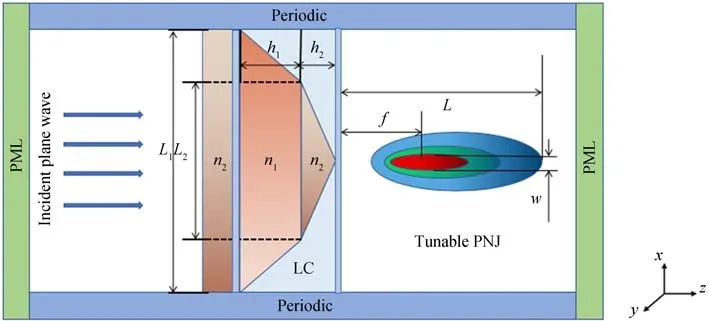
图2 填充液晶微金字塔结构产生光子纳米射流示意Fig.2 Schematic of a micropyramid structure filled with liquid crystals producing PNJ
2 结果与分析
为研究以液晶为背景介质时,液晶分子的偏转对光子纳米射流性能的影响,需要对不同液晶偏转角下的光场分布进行仿真分析。分别令φ=0°、φ=20°、φ=40°、φ=60°、φ=80°,得到的仿真结果如图3(a)~(e)。

图3 不同液晶偏转角下的光场分布Fig.3 Distribution of light fields at different liquid crystal deflection angles
如图3,光波照射双层微金字塔结构会在出射场形成多个焦点。当φ=0°时,微结构产生的光子纳米射流只有一个光强值较大的焦点。随着液晶分子偏转角的增大,光子纳米射流第一焦点的焦距增加,光强值减弱,第二焦点处的光强值增强。这说明液晶分子的偏转对光子纳米射流的聚焦性能具有调制作用,基于此,将从光强、衰减长度、半高全宽几个方面进行具体分析。
2.1 对光子纳米射流光强的调制作用
设置φ值分别为0°、20°、40°、60°、80°,观察焦点的光强变化,如图4,Focal1为第一个焦点处的光强变化,Focal2为第二个焦点处的光强变化。
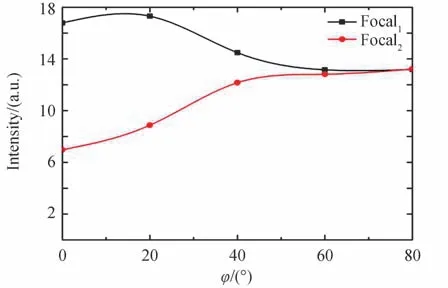
图4 不同φ 值对应的光子纳米射流光强值Fig.4 PNJ intensity values corresponding to different φ angles
由图4 可知,第一个焦点处,随着φ的增加,光强值趋于减小,由17.707 6 mW/cm2降为13.161 1 mW/cm2。第二个焦点处的光强值呈现上升趋势,由6.968 79 mW/cm2上升为13.489 8 mW/cm2。两个焦点的能量接近互补,并都在φ=50°左右时保持平衡,这是背景介质折射率增加,微结构与背景折射率之比变小引起的。微结构与背景折射率之比越大,焦点会越靠近微结构并嵌入微结构内部。相反,微结构与背景折射率之比越小,焦点越远离微结构,上述结论与前人研究相符[18]。并且由于入射条件相同,入射能量保持不变,根据能量转换定律,第一个焦点处的能量随微结构背景折射率的增加向第二个焦点处转移[19]。
2.2 对光子纳米射流衰减长度的调制作用
衰减长度是表征光子纳米射流的重要指标之一。φ值为0°、20°、40°、60°、80°时光子纳米射流沿z轴方向的焦距如表1 所示。其中,f1代表第一个焦点的焦距,f2代表第二个焦点的焦距。

表1 不同φ 值对应的第一和第二焦距Table 1 The first and second focal lengths corresponding to different φ angles
结合图4 与表1 可以看出,第一个焦点处的光强值达到稳定,即φ=50°左右时焦距变大,由9.3 μm 增加到12.3 μm,第二个焦点的焦距由24.4 μm 增加到24.8 μm。这表明随着微结构与背景折射率之比的减小,焦点也在逐渐远离微结构,实现了从6.1λ到22.3λ的可调焦范围。
将f1相同的φ=20°和φ=40°产生的光子纳米射流沿z方向强度分布进行对比,如图5(a)。f1不同的φ=0°和φ=80°产生的光子纳米射流沿z方向强度分布,如图5(b)。
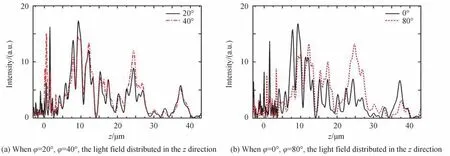
图5 不同液晶旋转角 φ 对光子纳米射流焦距和衰减长度的影响Fig.5 The effect of the different liquid crystal rotation angle φ on the focal length and attenuation length of the PNJ
由图5(a)可知,在z=9.3 μm 处φ=20°的光强值明显大于φ=40°,但第二个焦点z=24.4 μm 处,φ=40°的光强值反而远远大于φ=20°。这说明随着φ值的增大,第一焦点处的能量开始向第二焦点处转移。从图5(b)可以看出,当φ=0°时,焦距较小且能量聚集在第一个焦点上,衰减长度达到了36.5λ。当φ=80°时,焦点后移,能量平均分布在两个焦点上,使第二个焦点处的光强值也够大。但衰减长度只有25.9λ,且横向宽度也更大。结果表明,随着液晶折射率的增加,在保持较高光强值的前提下,焦距的延长是以牺牲纵向长度和横向宽度为代价的。
2.3 对光子纳米射流半高全宽的调制作用
φ值分别为20°、40°、60°、80°时两个焦点处的半高全宽与聚焦效率如表2。第一个焦点处的横向分布如图6。半高全宽为焦点处峰值一半的点之间的距离,聚焦效率为焦平面上以三倍半高宽为直径的区域内能量与总能量之比。

表2 不同φ 值对应的两个焦点处的聚焦效率和半高全宽Table 2 The focusing efficiency and half-height full width of the two focal points corresponding to different φ values

图6 不同φ 值光子纳米射流焦点处的横向分布Fig.6 Lateral distribution at the focal point of the PNJ corresponding to different φ values
由表2 和图6 可以看出,随着周围介质折射率的增加,两个焦点处的FWHM 和聚焦效率都呈现出上升的趋势。第一个焦点处FWHM 调节范围为0.89λ~1.23λ,聚焦效率调节范围达到了29.4%~40.1%。第二个焦点处FWHM 调节范围为0.90λ~1.19λ,聚焦效率调节范围达到了16.9%~43.2%。针对f1,微结构与背景介质折射率之比越大,光子纳米射流会变窄以提供更强的聚焦[20]。减小微结构与背景介质折射率之比,光强值减弱,FWHM 增加,聚焦效率也会随之增加。
2.4 纳米射流特征变化的理论分析
对比分析有无液晶这一背景介质对光子纳米射流的影响,无液晶与ITO 极板的微结构光场分布仿真结果如图7。

图7 无液晶微结构光场分布结果Fig.7 Result of the light field distribution produced by the microstructure without liquid crystal
根据仿真结果,不加液晶时的焦距为2.3λ,衰减长度为5.8λ,远小于加液晶的最大焦距22.3 μm 与最大衰减长度36.5λ。且不加液晶时的光强值为19.3 mW/cm2,FWHM 为0.88λ,与加液晶的最大光强值与最小FWHM 相近。综上所述,不加液晶的微结构光场的强度与半高全宽与液晶存在时的光场结果相近,其焦距与衰减长度远小于液晶存在时的结果,并且液晶能赋予光场多样性,具有对光场的调控能力。
光子纳米射流由于尺寸与波长相当,不能用几何光学来解释,只能用Mie 散射近似解释,目前只有微球粒子有相关理论被提出。对于微球粒子,Mie 散射理论有两个重要的强度分布函数

式中,a=2πr/λ为尺度参数(r为粒子半径,λ为入射光的波长),m为粒子的相对折射率,即粒子与所处介质的折射率之比,θ为散射角。
强度分布函数中的系数

当粒子被一束非偏振光照射时散射光强度分布为

利用Mie 散射理论,可以得出相对折射率越小,光场的光强度最大峰值越小的结论[21],与本文结果一致。
3 结论
本文提出了一种异质材料双层微金字塔结构耦合空间光调制的光子纳米射流光学元件,通过FDTD 数值模拟,改变液晶分子的旋转角,减小微结构与背景折射率之比,实现光子纳米射流的动态可调谐。仿真分析结果表明,折射率对比度减小对异质材料双层微金字塔结构光子纳米射流的影响主要体现在焦点处横向宽度和聚焦效率变大、焦距增加、能量后移并出现多焦点等方面。焦距变化范围由6.1λ达到了22.3λ,衰减长度最长达到36.5λ,与双层微球结构耦合液晶PNJ 相比提高了10λ。随着微结构与背景介质折射率之比的减小,焦点逐渐远离微结构,能量向远场传输。此时,半高全宽增大,聚焦效率的调节范围可以达到16.9%~43.2%。可见,借助于液晶这一空间光调制手段,双层微金字塔结构光子纳米射流实现了大范围的焦距调节和超长的传播长度,在微粒操纵和光电探测领域表现出广阔的应用潜力。
