基于交叉椭圆飞秒激光光束的多丝阵列全光调控

曾涛，许龙，吴正茂

（1 西南大学 物理科学与技术学院，重庆 400715）

（2 微纳结构光电子学重庆市重点实验室，重庆 400715）

0 Introduction

Femtosecond filamentation phenomenon has attracted extensive interest during the last two decades.Due to extended plasma channels，high intensity preserving for a long distance and fruitful nonlinear interaction processes，femtosecond filaments have appeared as a promising medium for a wide range of applications，such as terahertz generation［1-3］，remote sensing［4-5］，lightning control［6-7］，waveguiding［8-9］，pulse shortening［10-11］，and light induced breakdown spectroscopy［12-13］.

When femtosecond laser beam power is much larger than the critical power for self-focusing，the beam breaks up into multiple filaments，which originates from the modulation instability of the wave-front and leads to random filament spatial distribution［14-15］.Multiple filaments are quite essential for multichannel white-light radiation［16］，terahertz generation［17-18］，phase-matched ultrafast Raman frequency conversion［19］，and waveguiding of microwave radiation［20］.These applications rely on the tailoring of filament parameters.It is worth mentioning that one of the most challengeable problems is to obtain high reproducibility and regular localization of multifilament pattern.Nowadays，the multifilament array has been realized based on amplitude masks［21］，beam ellipticity［22］，focusing with an axicon［23］，diffractive optical elements or a spatial light modulator［24-26］.

In Ref.［21］，Two-dimensional（2-D）arrays of filaments were created in water by launching the beam through appropriate apertures such as slits and meshes，superimposing a regular diffraction structure that could influence the multiple filaments pattern.Moreover，all filaments evolve nearly identically as if there were no competition.It has been demonstrated that an intense，highly elliptical laser beam could break up into highly reproducible periodic two-dimensional arrays of laser filaments，whose periodicity may be easily controlled by the input beam intensity［22］.By focusing on an axicon，regularization of multiple filaments in methanol solution could be realized and filaments located at the core and ring structures of the quasi-Bessel beam created by the axicon［23］.Femtosecond laser filament arrays consisting of two，four and eight filaments are generated in air by using step phase plates with π phase lag.Geometric features of the filament array，including the number of filaments and the distance among the filaments，could be controlled with an additional focusing lens［24］.A computer-controlled spatial light modulator has been used to manipulate the patterned optical fields and control the multi-focal spots in the focal plane.Thereby，femtosecond multi-filamentation with designable locations of filaments and strength of interaction between filaments has been realized［26］.In general，these approaches depend on control of beam wave-front amplitude，initial phase distribution or spatial waveshape by a kind of optical tuning devices.However，an all-optical switching approach to control the multifilament array has not been considered up to now，which would be particularly important for 2-D all-optical switching device or pumpprobe experiments based on multifilament arrays.

Recently，it has been demonstrated that，by using a second laser beam together with a nonlinear medium，people could realize an active control of laser beam polarization［27-29］.The modulation of the nonlinear medium refraction index by overlapping two laser beams results in the polarization transfer between the laser beams.This fact inspires us to consider that the two-beam style refraction index modulation would also allow for the manipulation of the transversal multifilament pattern without worrying about optics damage when the nonlinear medium is a plasma in air.

In this paper，a new type of optical control of switching on and off the multifilament array pattern based on two noncollinear elliptical femtosecond laser beams has been proposed.It is predicted that a reproducible and regular multifilament array pattern could be generated by overlapping the femtosecond laser beam with a second laser beam of both different and identical wave frequencies in air.The filament cluster number and spatial distribution of the multifilament array could be tuned by the crossing angle，laser beam power，ellipticity and frequency of the second femtosecond laser beam.Moreover，the multiple filaments could be significantly elongated by using this method.Cross-Phase Modulation（XPM）and the cylindrical symmetry breaking in the initial beam profile contribute to the 2-D multifilament array generation from the two noncollinear elliptical femtosecond laser beams with different frequencies.In comparison，interference plays a dominant role in the situation of the two femtosecond laser beams with identical frequencies.

1 Two noncollinear femtosecond laser beams with different frequencies

The schematic of studying the propagating of two noncollinear femtosecond laser beams in air are shown in Fig.1（a）.Fig.1（b）depicts the cross section of the initial input of two elliptical laser beams.The central wavelengths of beam 1 and beam 2 were chosen to be 800 nm and 700 nm，respectively.Since we mainly

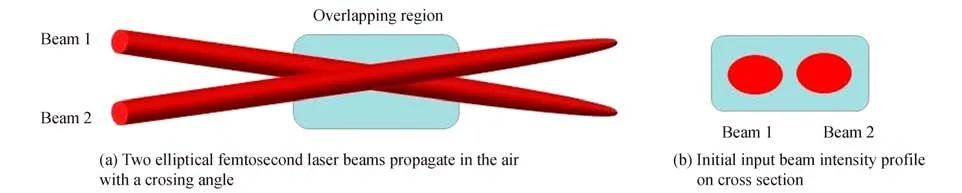
Fig.1 Schematic of the simulation process

focused on the spatial distribution of the two noncollinear femtosecond laser beams in air，the temporal aspects of the propagation could be ignored.The validity of this processing method has been demonstrated by previous studies［24，30-31］.Thus，the total electric field can be expressed as

whereA1andA2denote the amplitude of the laser beam 1 and 2，ω1andω2represent the frequencies of the two laser beams，k1andk2denote the wave number.

A three-order nonlinear polarization in a nonlinear medium could be produced by the laser field，given by

For slowly varying amplitude approximation，the propagation of laser beam 1 in a nonlinear medium obeys the wave equation

According to Eqs.（1）and（2），we can obtainPNL(ω1) as follows

Introducing Eq.（4）into Eq.（3）and bringing in the defocusing of plasma item，the equation of laser beam 1 propagating in the nonlinear medium can be expressed as

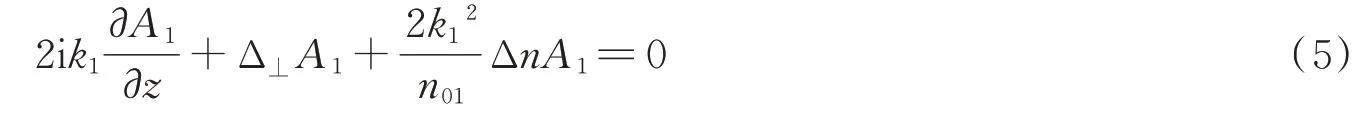
wherek1andn01represent the wave number and refractive index of beam 1 propagating in air，respectively.Δndenotes the intensity dependent refractive index，given by

The first item on the right of the above equationn2I1corresponds to the nonlinear refractive index induced by optical Kerr effect.n2is chosen to be 2.0×10-19cm2/W in air［32］.The second item denotes the nonlinear refractive index induced by intensity of beam 2 and indicates the effect of cross-phase modulation.The third item corresponds to the nonlinear refractive index induced by plasma defocusing effect andmis chosen to be 8，which is the effective nonlinearity order of multiphoton ionization rate［32］.αis an empirical parameter which gives rise to a clamped intensity of 5.0×1013W/cm2in our simulation［31］.Plasma defocusing has been considered as the counteracting effect to the self-focusing and cross-phase modulation.

Similarly，the wave equation of laser beam 2 propagating in air can be expressed as

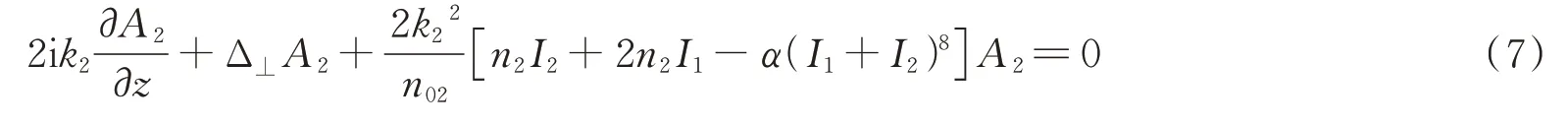
On the cross section of propagation distancez=0 as shown in Fig.1（b），the complex amplitudeA1andA2of laser beam 1 and 2 can be expressed as

wherer1xandr1yrefer to the radii of the initial elliptical beam 1 alongxlong-andyshort-axis directions，respectively.Similarly，r2xandr2ycorrespond to the radii of the initial elliptical beam 2 alongxlong-andyshort-axis directions.his the distance between the center of beam 1 and beam 2，which is set to be 0.2 mm.θis the angle between the two noncollinear laser beams.

In simulation，bothr1xandr2xare chosen to be 0.9 mm，whiler1yandr2yare 0.6 mm.The angleθis chosen to be 0.44°.The input powers of beam 1 and beam 2 are both set to be 10Pcr.HerePcrrefers to the critical power for self-focusing and is defined as

whereλis the wavelength，nandn2refer to the refractive index and nonlinear refractive index of air，respectively.

The numerical simulation of the two noncolinear femtosecond laser beams with central wavelengths of 800 nm and 700 nm propagating in air is carried out based on Eqs.（5）and（7）synchronously.The simulation result is shown in Fig.2.The initial elliptical profile of the two laser beams at distancez=0 is given in Fig.2（a）.Figs.2（b）～（h）depict the evolution of the beam profile obtained by the incoherent superposition of two laser beam intensity distribution on the cross section at different propagation distances.In detail，Figs.2（b）～（e）show that the maximum beam intensity increases versus the propagation distance，indicating the self-focusing process of the two elliptical laser beams in air.As shown in Fig.2（e），the beam intensity is clapped at around 4.5×1013W/cm2fromz=35 cm，indicating the occurrence of laser filaments.Meanwhile，multiple filament stripes are produced at this distance.The two laser beams start to intersect at aboutz=10 cm in Fig.2（b）and depart from each other atz=45 cm as in Fig.2（f）.Thus，the overlapping region is between 10 cm and 45 cm，almost corresponding to the whole self-focusing process.The two laser beam centers overlap atz=26 cm in Fig.2（d），where the two laser beams intersect thoroughly.Fig.2（f）shows that multiple filaments are observed as multiple laser spots atz=45 cm.And then a regular 2-D multifilament array was formed at the distance of 50 cm as in Fig.2（g）.Further，the filament cluster number in the multifilament array increases with the propagation distance as shown in Fig.2（h）.

Fig.2 Simulation results of two elliptical femtosecond laser beams propagating in air with a crossing angle 0.44°.Transverse pattern of laser beams intensity distribution at different distances

Since the spatial asymmetric distribution of the initial input laser pulse could result in the beam breaking up，the ellipticity of the initial laser beams contributes to the formation of multiple filaments.Also，cross-phase modulation could significantly enhance the asymmetry of the laser beams' phase front in another way when two laser beams overlap.Therefore，the generation of the 2-D multifilament array originated from both the ellipticity and cross-phase modulation of the two femtosecond laser beams.

Since the critical power for self-focusingPcris related to the beam wavelength，as indicated by Eq.（10），the input power of beam 1 with wavelength of 700 nm is slightly less than that of beam 2 with wavelength of 800 nm.As shown in Fig.2（a），the intensity distribution of two beams are not symmetrical withx=0.This indicates that the electric field distributions of two beams is not symmetrical withx=0 as well，including both the amplitudes and the frequencies.For the nonlinear propagation of two beams based on Eqs.（5）and（7），the nonlinear refractive index induced by optical Kerr effect for the two beams are different，which rely on the beam intensities of beam 1 and 2.Moreover，nonlinear refractive index induced by the effect of cross-phase modulation for the two beams are different as well.In addition，the self-focusing distances of the two laser beams propagating individually without interaction are also different，which rely on the position for the occurrence of filaments.The self-focusing distance could be deduced from the following equation.

Here，zfis the self-focusing distance of the beam.Pin/Pcris the ratio between the input power and critical power for self-focusing of the laser beam，which is chosen to be 10 for both beams in our simulation.LDFis the Rayleigh diffraction length，which depends on the wavenumber and size of the laser beam.Therefore，all the above factors result in the fact that the intensity distribution is not symmetrical withx=0 for the Figs.2（e）～（h）.

In order to investigate the effect of beam ellipticity on the multifilament pattern generation，the propagation of two noncollinear Gauss femtosecond laser beams without ellipticity in air has been simulated.Fig.3（a）shows the initial input beam profile of the two laser beams atz=0，whose beam widths are both 0.73 mm alongxandydirections.The angle between two crossing laser beams is set to be 0.44° as well.The overlapping region is between 10 cm and 35 cm，which is similar to that in Fig.2.Laser filaments occur at aroundz=35 cm with a clapped beam intensity of about 4.5×1013W/cm2.As shown in Fig.3（h），multifilament array pattern is clearly produced atz=55 cm，mainly resulting from cross-phase modulation effect.Compared with two crossing elliptical beams，the multifilament array generated by two crossing Gauss beams in Fig.3（h）is less regularly distributed than those in Fig.2（h）.

Fig.3 Simulation results of two Gauss femtosecond laser beams propagating in air with a crossing angle 0.44°.Transverse pattern of laser beams intensity distribution at different distances

For a Gauss beam with laser power of many times the critical power，the input beam modulational instability leads to beam breaking up and multiple filaments occur.Under this condition，the number and the location of the filaments are unpredictable.For an elliptical laser beam，the multiple filamentation pattern induced by small input beam ellipticity appears as a result of nucleation of annular rings surrounding the central filament.Moreover，the input beam ellipticity can dominate the effect of transverse modulational instability，regularizing the nucleation of annular rings and resulting in predictable and highly reproducible multiple filamentation patterns.

The focused beam of a Gauss laser beam by means of a focal lens would have a small intrinsic ellipticity.The elliptical beam can be formed by insertion of a slightly off-axis iris into the beam path.The ellipticity can be tuned by changing the position of the iris in the transverse plane.Another method to yield the elliptical beams has been used by adjusting the beams to the edges of the lens and concave mirror［33］.In addition，by focusing a laser beam with a cylindrical lens，a highly elliptical beam would be obtained.

Considering the propagation of the two elliptical femtosecond laser beams individually without any interaction effect between two beams，the result is depicted in Fig.4.Fig 4（a）is the initial profile of the two beams atz=0 whose parameters are the same with those in Fig.2.Fig.4（d）shows that a laser filament is produced by beam 2 with central wavelength of 800 nm atz=35 cm，while beam 1 with wavelength of 700 nm breaks up and the filament occurs atz=40 cm as in Fig.4（e）.Fig 4（f）shows that beam 1 and beam 2 tends to split atz=45 cm.Moreover，two laser filament spots are formed in both horizontalxdirection and verticalydirection for beam 2，while three laser filament spots occur alongxdirection for beam 1 as illustrated in Figs.4（g）and 4（h）.This result indicates that without cross-phase modulation effect between two crossing laser beams，much fewer multifilament laser spots can be observed from the elliptical laser beams.

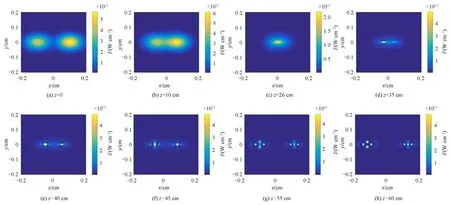
Fig.4 Simulation results of two elliptical femtoseoncd laser beams propagating in air individually with a crossing angle 0.44° and without any interaction between two laser beams.Transverse pattern of laser beams intensity distribution at different distances

The filament cluster number as a function of propagation distance for the above three conditions of Figs.2～4 are depicted in Fig.5（a），including two crossing elliptical beams as the black solid line，two crossing Gauss beams as the red dot line and two individual elliptical beams without cross-phase modulation as the blue dashed line.Here，a filament cluster is thresholded to a fixed beam intensity of 1.0×1013W/cm2on the cross section.Generally，the filament cluster number increases with the propagation distance step by step.The sharp increase in one step indicates the filament splitting process due to transverse modulation instability of wave-front.For the condition of two crossing elliptical beams，the splitting of one filament cluster starts at 30 cm，while this splitting process for the other two conditions starts at around 35 cm.Both the ellipticity of beams and crossphase modulation intensify the wave-front perturbations，leading to the filament splitting for two crossed elliptical beams at an early stage.In addition，the filament cluster number for two Gauss beams is slightly less than that of two elliptical beams，while the filament cluster number for two individual elliptical beams without cross-phase modulation is less than that of the other two conditions.

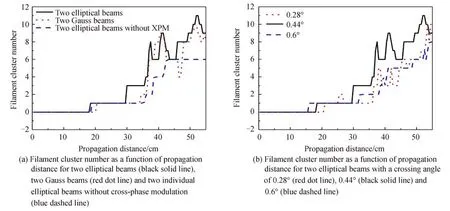
Fig.5 Filament cluster number as a function of propagation distance

Furthermore，the influence of the angle between two laser beams on the multifilament pattern generation is investigated.Fig.6 is the result for a smaller angle of 0.28° between the two elliptical beams.The initial input parameters in Fig.6（a）are the same with those in Fig.2（a）.Both two beams break up atz=35 cm and laser filaments are formed as in Fig.6（d）.The centers of the two laser beams intersect atz=41 cm after the filament occurs as in Fig.6（e），where multiple filaments are observed.The two laser filament spots depart with each other atz=55 cm as in Fig.6（g）and a multifilament array pattern is generated atz=65 cm as in Fig.6（h）.It is noticed that the multifilament array pattern in Fig.2（h）is much more regular than that in Fig.6（h）.Moreover，as shown in Fig.5（b），the filament cluster number of the two crossing elliptical beams with an angle of 0.28° is less than that with an angle of 0.44°.This can be attributed to the fact that cross-phase modulation effect during the self-focusing process between the two laser beams with a larger crossed angle can bring more significant asymmetry of the wave-front when the two beams intersect before the filament occurs than after the filament occurs.

Fig.6 Simulation results of two elliptical femtosecond laser beams propagating in air with a crossing angle 0.28°.Transverse pattern of laser beams intensity distribution at different distances

For the situation with a relative large angle 0.6° between the two crossed elliptical laser beams，the result of the laser intensity cross-section pattern evolution is shown is Fig.7.The centers of the two laser beams intersect atz=19 cm as in Fig.7（c），which refers to an initial stage of the self-processing process.The overlapping region of the two laser beams is almost betweenz=10 cm as in Fig.7（b）andz=30 cm as in Fig.7（d）.The filament starts to occur atz=35 cm as in Fig.7（e）.As shown in Fig 7（g），the number of the laser spots in the multifilament array pattern is much less than that in Fig.2（h）with the crossing angle of 0.44° between the two beams.This also can be deduced from the result of the filament cluster number as a function of propagation distance in Fig.5（b）.It is true that both larger crossing angle and interaction effect between the two beams during the self-focusing process will lead to more significant asymmetry of the laser beam phase front.However，since the two beams overlap at the initial stage of the self-focusing process，the cross-phase modulation effect is quite weak due to the relative low beam intensity cross-section distribution.

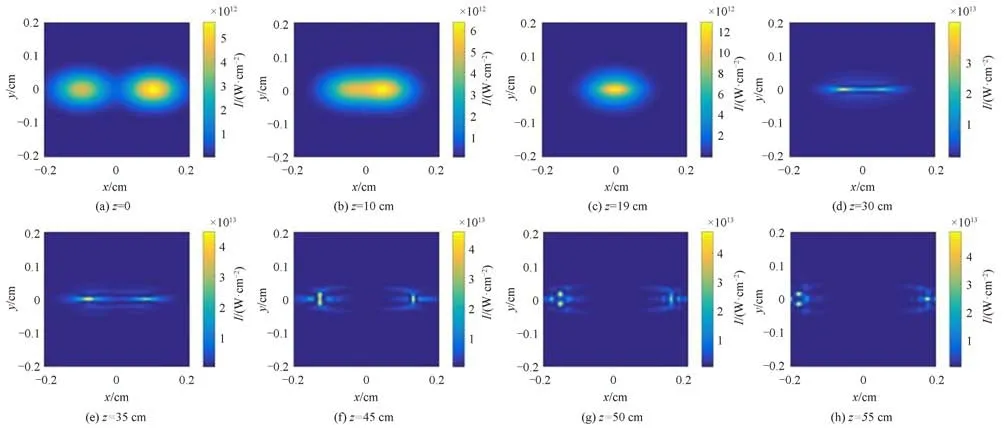
Fig.7 Simulation results of two elliptical femtosecond laser beams propagating in air with a crossing angle 0.6°.Transverse pattern of laser beams intensity distribution at different distances

For the two non-collinear beams with different frequencies，phase cross modulation could enhance the asymmetry of the pulse’s phase front when two beams cross each other.As indicated in Fig.2（c），fory=0 alongxdirection，since the right part of beam 1 intersects with beam 2，the right part of beam 1 suffers stronger phase modulation than the left part for higher total beam intensity.However，this asymmetry does not occur along y direction.This phenomenon also happens to beam 2.Therefore，due to the crossing angle between two laser beams，the phase cross modulation leads to symmetry breaking of the pulse phase and promotes the generation of multiple filamentation array.Increasing the crossing angle between two laser beams does reduce the interaction length.As shown in Fig.7（h）with a larger crossing angle of 0.6°，less filaments are generated than that in Fig.2（h）with a crossing angle of 0.44°.However，for a smaller crossing angle or even 0，the asymmetry of the pulse's phase front based on phase crossing modulation will be suppressed.As indicated in Fig.6 with a smaller crossing angle of 0.28°，the filament number is less than that in Fig.2 as well.Finally，a compromised angle of 0.44° was chosen for optimizing the multiple filamentation array.

In addition，the intensity contours for two crossing beams with different angles are displayed in Fig.8，which is thresholded to a beam intensity of 1.0×1013W/cm2.This result further confirms that the multifilament array pattern produced with a crossing angle 0.44° is much more regularly distributed than that of a lower angle 0.28° or a higher angle 0.6°.

Fig.8 Transmission of two crossing femtosecond laser beams in space with different angles

In experiments，the spatial distributions of the filament arrays can be characterized as follows，including both the longitudinal distributions and transverse patterns.The longitudinal distributions can be investigated by side imaging of the scattered white light produced by the filaments.A microscopy objective and a CCD camera would be used to capture the filament array images.For the transverse distributions，the transverse patterns of the filament arrays can be recorded straightforwardly by burn paper.By quickly sweeping the burn paper across the propagation direction，the single shot laser burn spots would be obtained.Combining the above two methods，the number of filaments could be obtained as a function of the propagation distance.Besides，the cross sections of the laser beam could also be investigated as a function of the propagation distance by the following method.Two parallel fused silica wedges are inserted in the laser beam path at grazing angles，yielding a reflectivity of about 10% at each front surface.After two surface reflections the laser intensity can be reduced to approximately 1%.Then，the cross sections of the laser beam pattern could be registered by a CCD camera through an imaging system.A bandpass filter should be put in front of the CCD camera to filter out the scattered white light.Moving the wedges and the CCD together longitudinally，the evolution of the laser beam pattern and the filament number as a function of the propagation distance could be obtained finally.

2 Two noncollinear femtosecond laser beams with identical frequencies

For the propagation of two noncollinear elliptical femtosecond beams with identical frequencies，the corresponding numerical simulation model is based on（2D+1）-dimensional nonlinear wave equation as follows［34］

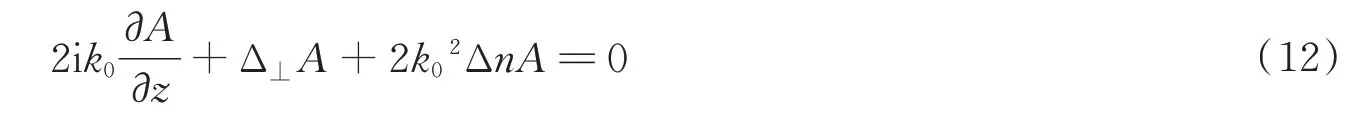
whereAis the complex amplitude of the light field，k0is the wave number corresponding to a wavelength of 800 nm in our simulation，Δn=n2I-αImis the nonlinear refractive index attributed to the optical Kerr effect and plasma defocusing.

Since the wavelengths of beam 1 and beam 2 are identical，the total complex amplitude can be obtained by the superposition of the two beams directly.Thus，the initial elliptical laser beams can be expressed as

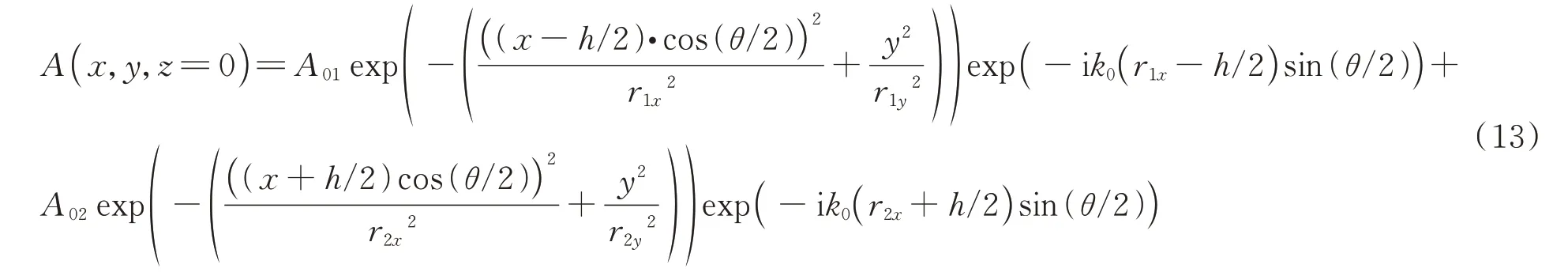
whereA01andA02are the amplitude of beam 1 and beam 2，respectively.The initial input beam parameters，such as elliptical beam widths，distance between two beamsh，and the angle between two beams，are all set to be the same with Fig.2.

The evolution of the beam intensity pattern for the two crossing femtosecond laser beams with identical frequencies propagating in air is shown in Fig.9.Fig.9（a）refers to the initial laser beam shape，displaying interference stripes in the central intersection area.The number of stripes get increasing when the centers of the two beams get closer as shown in Fig.9（b）.The laser filament occurs at aroundz=25 cm with a clapped maximum beam intensity of about 5.0×1013W/cm2.The self-focusing distance is much shorter than that of two beams with different frequencies in Fig.2，resulting from a higher laser beam power by the coherent superposition of two beams with identical frequencies.A regular 2-D multifilament array is generated atz=35 cm as in Fig.9（e）.The laser array merges into several laser filament spots with propagation distance as in Figs.9（f）～（h）.Moreover，this process is clearly depicted in Fig.10（a），which is the intensity contour thresholded to a beam intensity of 1.0×1013W/cm2.Fig.10（b）shows the filament cluster number as a function of propagation distance.The filament cluster number reaches a highest value at aroundz=30 cm and then decreases with the emerging of the laser filament spots.The multifilament array with a larger filament number than that in Fig.2 results from the modulation instability of the wave-front dependent on both the ellipticity and the interference effect of the two beams.Therefore，the multifilament array pattern could also be tuned by the frequency of a second laser beam.

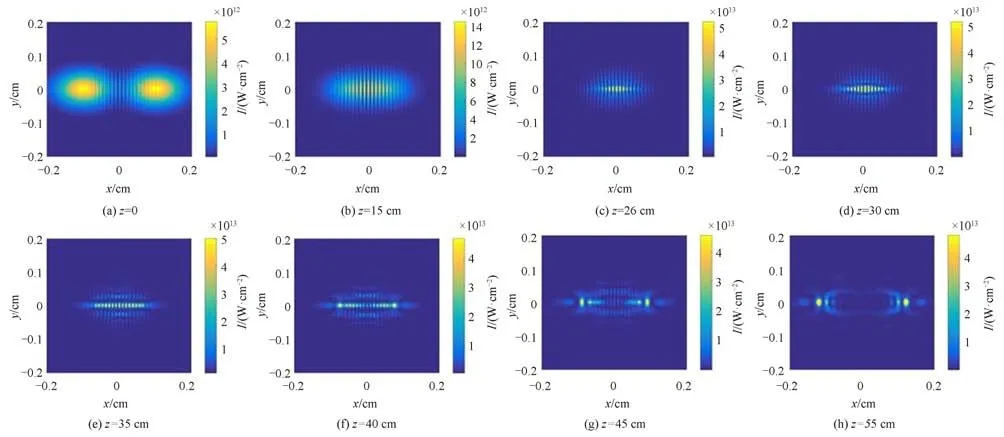
Fig.9 Simulation results of two elliptical femtosecond laser beams propagating in air with identical frequencies and a crossing angle 0.44°.Transverse pattern of laser beams intensity distribution at different distances

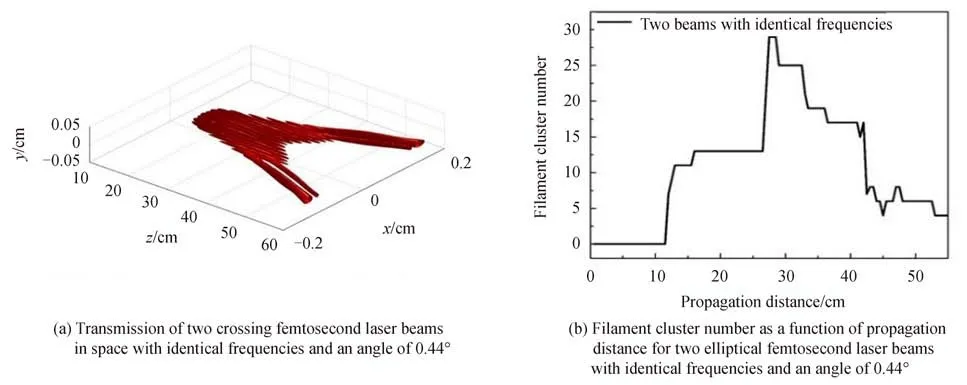
Fig.10 Transmission of two crossing femtosecond laser beams in space with identical frequencies and the corresponding filament cluster number as a function of propagation distance

For the case of two laser beams with identical wavelengths in Fig.9，the electric field distribution of the two input beams are totally symmetrical withx=0.Thus，the intensity distribution is symmetrical withx=0 at any propagation distance，which is distinctly different with that in Fig.2.

Considering two collinear femtosecond beams with identical frequencies propagating in air，it has been proved that the spatial intensity distribution depends on the phase relation between two light fields［35-36］.Inphase pulses tend to form a unified filament，while out-of-phase pulses lead to two filaments.If an angle between two beams exists，they can pass through each other and an interference pattern can be formed，resulting in the generation of a multiple filamentation array，as shown in Fig.9.

When considering the total light intensity under the interaction of two beams with closed frequencies，it would be the incoherent sum of the two beam intensities directly without a coherent term.Thus，if the frequencies of the two beams are 790 nm/799 nm and 800 nm，in theory，the nonlinear propagation of the two beams should be simulated separately based on Eqs.（5）～（7）.The nonlinear refractive index induced by the cross-phase modulation and the plasma defocusing effect-induced nonlinear refractive index depends on the incoherent sum of the two beam intensities for each laser beam propagation.Therefore，the main mechanisms affecting multifilament array pattern are the same as the situation of unequal frequencies in theory，without considering the bandwidth of the femtosecond laser pulse.

In the experiment，one method to conduct the two noncollinear femtosecond laser beams with different frequencies is as follows.The femtosecond laser pulse with spectral width of about 40 nm and central wavelength of 800 nm could be split into two beams.One beam is spectrally broadened in a hollow fiber filled with krypton gas.And then the broadband spectrum is dispersion compensated by chirped mirrors and glass wedges.Passing through a bandpass filter，a femtosecond laser beam at 700 nm center wavelength with 40 nm bandwidth can be obtained finally.The other beam at 800 nm central wavelength passes through a delay stage.Adjusting the delay stage and the beam path，two noncollinear femtosecond laser beams with different frequencies could be realized.Considering the experimental conditions，the spectral width of the two femtosecond laser beams is about several tens of nanometers in most cases.If the central wavelengths of the two beams are 790 nm/799 nm and 800 nm，the spectrum of the two beams overlap a lot.For the spectral region of the two beams with identical wavelengths，the interference stripes occur.The character of multiple filaments pattern would be determined by the interference pattern and the number of fringes within which the peak power exceeds the critical value for filamentation.For the spectral region of the two beams with different wavelengths，cross-phase modulation contributes to the multifilament array generation.

The simulation results in this paper would meet the condition of the vertical polarization of two beams，which refers to the polarization direction perpendicular to the overlapping plane.For the horizontal polarization of two beams，though there exists a small angle between the polarization directions of two beams due to the crossing angle，it could be neglected in the simulation process.For the situation of the two beams with different frequencies，the horizontal or vertical polarization direction of the two laser beams would hardly influence the nonlinear refractive index induced by the cross-phase modulation and the plasma defocusing effect-induced nonlinear refractive index which depends on the incoherent sum of the two beam intensities.For the situation of the two beams with identical frequencies，the influence of the horizontal or vertical polarization direction on the interference effect could also be neglected.In addition，it has been proved that polarization effects for the filamentation of a single laser beam are important only when the radius of a single filament can be comparable with the wavelength.In our simulations，the filament radius is around one hundred micrometers，while the beam wavelength is chosen to be several hundred nanometers.Therefore，as long as the two beam polarization directions are identical，the direction of linear polarization of the incident beam would have no effect on the orientation of the filament array pattern.

3 Conclusion

In a summary，a simple approach to realize the optical switch of a regular and reproducible multifilament array pattern based on two noncollinear elliptical femtosecond laser beams has been presented in this paper.The filament cluster number and spatial distribution of the multifilament array could be tuned by the ellipticity，crossing angle，beam power and frequency of a second femtosecond laser beam.The regular multifilament array produced by two elliptical femtosecond laser beams with different frequencies mainly results from symmetry breaking in the initial beam profile and phase-cross modulation.Moreover，cylindrical symmetry breaking in the initial beam profile and interference contributes to the multifilament array produced by two elliptical femtosecond laser beams with identical frequencies.Our results could pave the way to some potential applications relying on multifilament arrays，such as terahertz generation or 2-D all-optical switching devices.