基于多信息融合和栈式自编码网络的扩散光学层析方法

孙志龙，张杰，刘宗洋，高峰，3，张丽敏，3

（1 天津大学 国际工程师学院，天津 300072）

（2 天津大学 精密仪器与光电子工程学院，天津 300072）

（3 天津市生物医学检测技术与仪器重点实验室，天津 300072）

0 引言

扩散光学层析（Diffuse Optical Tomography，DOT）作为一种新型的功能光学成像技术，其利用波长范围在600～900 nm 的近红外光入射生物组织体，根据在生物组织边界得到的光流量，从而重构组织内部光学特性的三维分布［1］。该技术具有无创、无电离辐射以及可提供生物组织生理学信息等优势，在乳腺肿瘤成像和脑功能成像等领域极具应用潜力［2-4］。在DOT 成像过程中，近红外光在组织中传播具有强散射特性，且边界测量数据远小于需要重构的组织体光学参数个数［5］。因此，为提高DOT 图像重建质量，国内外研究人员发展了多种图像重建优化算法。其中，常用的策略为非线性迭代算法中添加不同类型的正则化项，基本思想是在每次迭代过程中添加额外的惩罚项进行正则化约束，以抑制测量噪声和减小模型误差所带来的影响，从而获得不适定问题的稳定近似解。典型的正则化方法包括L1 范数正则化和L2 范数正则化［6］。基于L2 范数的正则化方法可有效的重建DOT 图像，但L2 范数具有平滑效应，对图像边缘恢复较差。L1 范数则可以保持边缘，但易出现阶梯效应，导致图像产生虚假边缘。此外，国内外学者提出将扩散光学层析成像技术与现有的医学成像模态结合发展成为多模态成像技术。如BROOKSBY B A 和邓勇等分别把磁共振成像（Magnetic Resonance Imaging，MRI）和微型计算机断层扫描系统提供的解剖结构图像作为结构先验信息，以Laplace 算子的形式引入到正则化方法中以提高DOT 图像重建质量［7-8］。实验结果均表明，多模态方法可以提高重构光学参数图像的空间分辨率和量化度。但是，多模态成像方法首先需要对结构图像进行分割，且图像分割的准确性取决于操作者的经验水平。此外，这些方法无法从根本上避免DOT 逆向问题的不适定性，导致图像空间分辨率低和量化度低，以及由于多次迭代导致重建耗时长。

近年来，人工神经网络以其抽象特征提取和识别、较强的模型构建和泛化能力被广泛应用于图像重建领域。FENG Jinchao 等提出了基于反向传播神经网络（Back Propagation Neural Network，BPNN）的DOT图像获取方法，通过直接建立边界光信息与吸收系数的对应关系，克服逆问题求解的不适定性，但BPNN 训练速度较慢并且模型泛化能力不足［9］。YEDDER H B 等和YOO J 等提出基于卷积神经网络的DOT 图像重建方法。神经网络泛化能力进一步提高，但是网络参数较多，计算量更大，对于计算机性能要求高［10-11］。在各种神经网络中，栈式自编码（Stacked Auto-Encoder，SAE）具有网络模型简单，需要调整的网络参数少，网络训练速度快的优点。此外，SAE 的无监督预训练过程，可为多层神经网络训练找到一个良好的初始权重和偏差，有利于抑制输入数据中的噪声干扰，并在基于误差反向传播算法的微调过程中减少训练时间［12］。目前，基于人工神经网络的DOT 图像重建研究多对规则的圆形异质体进行图像重建，但针对形状欠规则异质体的图像重建还没有相关研究。

为此，本文面向DOT 技术在乳腺肿瘤成像中的实际应用，发展了基于多信息融合和SAE 网络的DOT图像重建方法。该方法将MRI 获取的解剖图像与DOT 中测量得到的边界光流量经过预处理后作为输入值，经过SAE 网络模型，最终输出DOT 光学参数图像。为验证该方法的有效性，本文进行了基于圆形和椭圆形的单异质体以及双异质体模拟。并与无结构图像先验信息时的基于SAE 的DOT 成像结果进行了对比。此外，设置了平均绝对值误差、均方误差和定量重建率三个指标对图像重建质量进行评估。

1 研究方法

1.1 光在生物组织中的传播

对乳腺组织等较厚组织体，近红外光在其内部的传输规律可由扩散方程，即辐射传输方程的一阶球谐展开近似描述。其中，稳态扩散方程描述为

式中，D(r)=c/(3μs'(r))为扩散系数，c为组织内光速，μ's(r)为约化散射系数，μa(r)为吸收系数，Φ(r，rs)为光子密度，δ(r，rs)表示在r处的迷向光源。为求解上述方程常结合Robin 边界条件

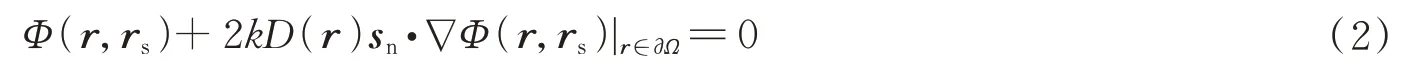
1.2 基于SAE 神经网络的图像重建

基于神经网络的DOT 图像重建策略摒弃了求解反向问题的复杂和耗时过程。本文只有吸收系数μa是需要重建，约化散射系数为已知常数。以未融合先验信息时基于SAE 网络的DOT 图像重建为例，网络的输入数据为边界光流量Φi(i=1，2，3，...，m)，输出数据集为相应的吸收系数μa，j(j=1，...，N)。其中，m为测量数据个数，N为有限元节点数。

1.2.1 栈式自编码器网络模型

本文使用的栈式自编码人工神经网络包含两个自编码器（Autoencoder，AE），SAE 的训练过程包括无监督的预训练及有监督的微调两个过程［14-15］，如图1 所示。

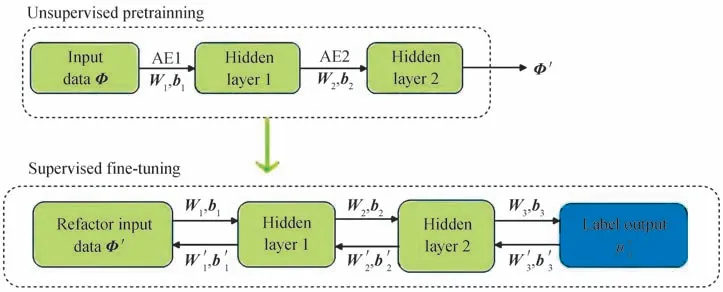
图1 SAE 训练过程Fig.1 SAE training process

在预训练阶段，第一个AE1 器将原始输入数据Φ映射到SAE 网络的第一个隐藏层，通过最小化重构误差获得网络的权重W1和偏置b1。随后第二个AE2 器将第一个隐藏层的输出结果作为其输入，继续最小化重构误差获得网络权重W2和偏置b2。在无监督预训练结束后，添加全连接层作为SAE 的输出层并对网络整体的权重及偏置进行微调。预训练得到的权重和偏置Wk，bk（k=1，2），被用作各神经层间权重和偏置的初始值。SAE 网络第二个隐藏层和输出层之间的权重W3和偏置b3被随机初始化。最后网络基于误差反向传播原理

通过计算预测输出值和期望输出值间的均方误差来最小化其损失函数，以求对网络模型中的权重和偏置进行微调得到最佳的参数。其损失函数定义为

式中，μa，j和分别为第j个样本的实际值和神经网络预测值，N为总的数据集样本数。

朝堂之上，七八位大臣对皇上说，你再不把秀容月明调回来，秀容兵就拥他为王了。皇上说，我要听你们的，就是中了胡人的离间之计。

1.2.2 自编码AE 网络

AE 是一种由编码器和解码器组成的无监督学习神经网络模型，如图2［16］所示。编码器作用是将输入数据的特征提取至隐藏层，而解码器将输入数据从隐藏层中重构出来。AE 网络的训练过程使得输入和输出大小相同，主要原理描述为

图2 自编码器网络结构图Fig.2 Autoencoder network diagram

对于编码过程，对AE 网络的输入：m个输入样本Φi（i=1，2，3，...，m）进行编码处理，通过式（4）的编码函数f对原始输入Φ编码，输出到隐藏层向量hk(k=1，...，n)，n为隐藏层神经元个数

式中，W是一个n×m的权重矩阵，b1∈Rn是输入层与隐藏层间的偏置。

对于解码过程，通过式（5）的解码函数将隐藏层输出h映射到输出层，完成对输入样本Φ的重构

式中，WT是一个m×n的权重矩阵，b2∈Rm是隐藏层与输出层间的偏置，Φ'表示对原始输入数据Φ进行重构后的信息。AE 网络最终训练的结果为Φ'=(f(Φ))≈Φ，保留输入数据的主要特征，降低数据中的噪声影响。

为了得到模型的最优参数W、WT、b1、b2，通过计算原始样本输入Φ和重构后的Φ'间均方误差来最小化其损失函数。

1.2.3 网络有监督微调阶段

SAE 网络有监督微调阶段主要包括：输入层（L0）、全连接隐藏层（L1）和预测输出层（L2）。人工神经网络进行微调原理图如图3 所示。

图3 网络微调原理图Fig.3 Schematic of network fine-tuning

使用已经初始化权重W[l]和偏差变量b[l]，根据迭代结果，计算输出层预测值和真实值μa的均方误差。将误差分摊给各层所有单元，从而获得各层单元的误差，进而调整各层之间的权重和偏差。本研究使用Adam 优化器基于学习率来控制神经网络的调整速度，激活函数使用的是Sigmoid 函数。

1.3 评价指标

为了定量评估两种方法在DOT 重构中的性能，计算了平均绝对误差（Mean Absolute Error，MAE）、均方误差（Mean Square Error，MSE）和定量重建率（Quantitativeness Ratio，QR）三个度量指标［17-19］

式中，μa，true(i)、μa，pre(i)分别是有限元节点第i处真实值以及神经网络预测的吸收系数。μˉa，pre为预测吸收系数的平均值，N为有限元节点总数。此处，MAE 和MSE 均用于评估重建图像与真实图像之间的误差。前者，MAE 计算了平均误差，MSE 同时计算了平均误差和标准偏差。QR 计算重建目标体吸收系数与真实吸收系数的比值，用于重建方法的定量性评估。理论上MAE 和MSE 越低，说明重建结果越好，QR 越接近100%，表示重建图像的吸收系数值越接近真实值。

2 结果分析

2.1 数据集的生成

在半径40 mm 的二维圆形仿体中嵌入异质体来模拟乳腺肿瘤组织，将仿体离散为8 762 个三角形和4 526 个有限元节点。为了生成用于神经网络训练的数据集，嵌入大小、位置和吸收系数不同异质体，其中，圆形异质体半径分别为6 mm、8 mm 和10 mm，椭圆异质体的半长轴变化范围为6～10 mm，半短轴变化范围为4～8 mm，步长均为2 mm。利用随机函数生成120 个异质体中心坐标；背景吸收系数设为0.003 4 mm-1，约化散射系数设为1 mm-1。异质体-背景的吸收系数的对比度（异质体吸收系数与背景吸收系数比值）为1.5～3.0，步长为0.5，约化散射系数与背景一致。双异质体与单异质体仿体生成基本一致，区别在于双异质体仿体内部有两个位置随机分布的异质体，且两异质体不重合。

设置共16 个同轴源探测对均匀布配在仿体的边界，如图4 所示。当某一光源激发时，除自身以及两侧邻近的位置外，共11 个位置探测，一组得到16×11（176）个测量数据用于图像重建。为了模拟真实测量值，在计算测量值中加入40 dB 的随机高斯噪声。

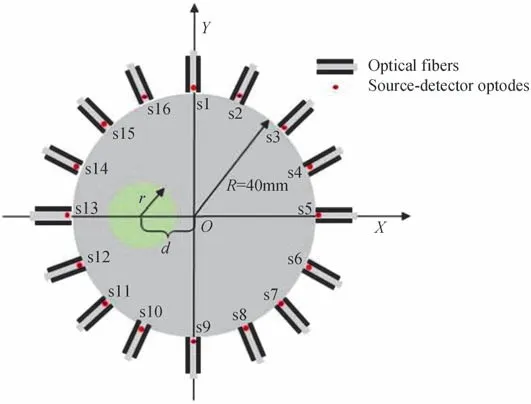
图4 二维圆形仿真模型Fig.4 2D circular simulation model

为了使得数据特征更加明显，需要对测量数据进行预处理

式中，Φbac是在仿体的光学参数均为背景值时测得一组边界光流量，Φ是加入异质体后测量得到的边界光流量，Φave为单个样本的平均值，σ为单个样本的标准差，经过数据预处理之后数据Φsca的均值为0，方差为1。

与光学仿体相对应模拟生成MRI 图像，如图5 所示。生成灰度图像的大小为51×51，总共2 601 个像素点，在输入网络之前做最大值最小值归一化预处理。将经过预处理的测量值（176）和灰度图像信息（2 601）进行融合，作为一组数据的输入（2 777），网络输出为吸收系数（4 526），共获得5 670 组样本数据，划分为训练集3 780 组，验证集1 620 组，测试集270 组。

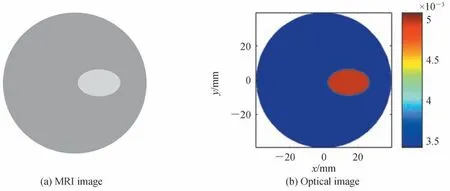
图5 模拟异质体分布的MRI 图像和对应的光学图像Fig.5 MRI image and corresponding optical image that simulate target distributions

对于SAE，根据经验将隐藏层1 和隐藏层2 的神经元数量分别设置为100 和300。此外，神经网络的学习率均设置为0.001，最小批次分别设置为20 组，预训练次数为2 000，微调次数为300。

2.2 数值模拟实验

为了评估和比较融合先验信息前后SAE 网络重建图像的性能，进行了一系列的数值模拟，并对实验结果进行了定性和定量的比较。主要对四种情况进行了对比。

1）随机分布的圆形异质体，目标体半径固定10 mm，吸收对比度分布为1.5、2.0、2.5 和3.0。图6 的第一行是无先验信息方法的重建图像（No prior），第二行是融合先验信息方法的重建图像（Prior），第三行是沿着穿过仿体和异质体中心线的吸收系数剖线，黑色圆圈代表真实异质体。

从图6 可以看出当异质体半径均为10 mm，在不同吸收对比度下，添加先验信息与否均可重建出异质体的位置和尺寸，且随着吸收对比度的提高，重建图像的质量均有所提高。当吸收对比度为1.5 时，无先验信息方法的重建图像中异质体边缘轮廓模糊，伪影较多，且吸收系数过高估明显，而融合先验信息方法对重建结果有明显的改善。

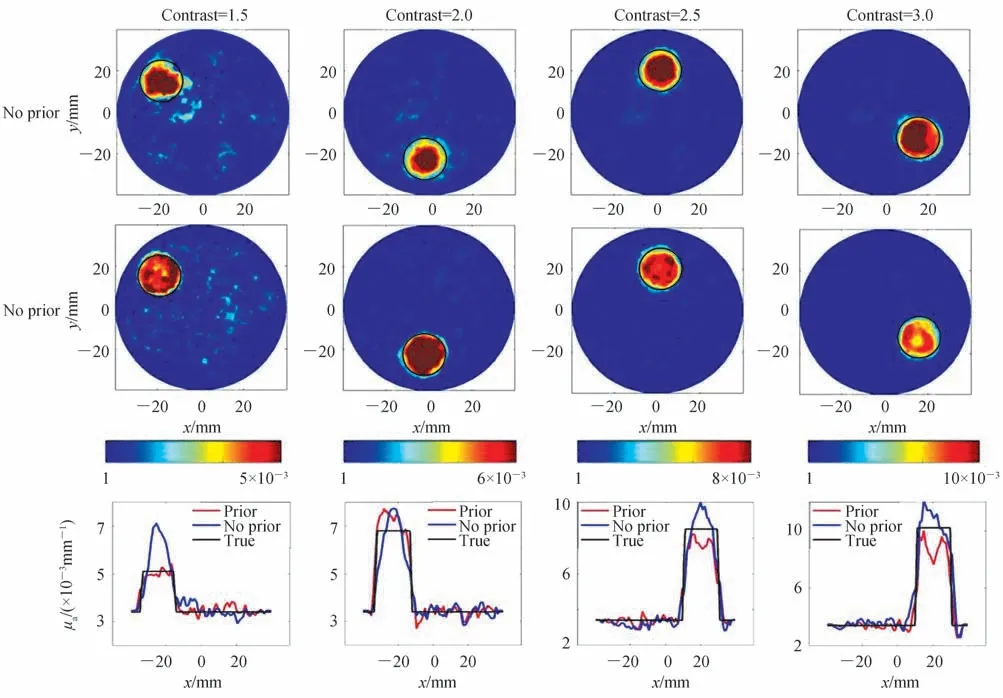
图6 不同吸收对比度下，基于无先验信息和融合先验信息的圆形单异质体重建及剖线Fig.6 Reconstructed images and profiles of a single circular target with different absorption contrasts based on no prior and prior methods

为进一步定量比较两种方法，表1 列出了重建图像的MAE、MSE 和QR 值，且为了容易对比，给出了表1对应的条形图（图7）。从表1 和图7 可以发现，融合先验信息方法的重建图像的MAE 均明显小于无先验信息方法所得的值，而MSE 仅在吸收比度为2 时略微大于无先验信息方法对应的值。其原因是吸收对比度为2 时，无先验信息方法获取的图像较真实值偏小，导致其标准偏差值偏小。此外，融合先验信息方法重建图像的QR 值也更加接近100%。定量分析表明融合先验信息方法图像重建质量更高。

图7 表1 对应的条形图Fig.7 Bar charts corresponding to Table 1

表1 圆形单异质体不同目标-背景吸收系数对比度重建图像评估指标计算结果Table 1 Calculation results of evaluation indexes for a single circular target reconstruction with different absorption contrasts

2）随机分布的圆形异质体，吸收对比度固定为3.0，半径分别为6 mm、8 mm 和10 mm。图8 是采用融合先验信息和无先验信息两种方法获得的重建图像以及对应的异质体吸收系数剖线。可以观察到两种方法均可较准确地重建图像，但是，小半径时，融合先验信息方法重建图像的轮廓更加清晰，且量化度更优。

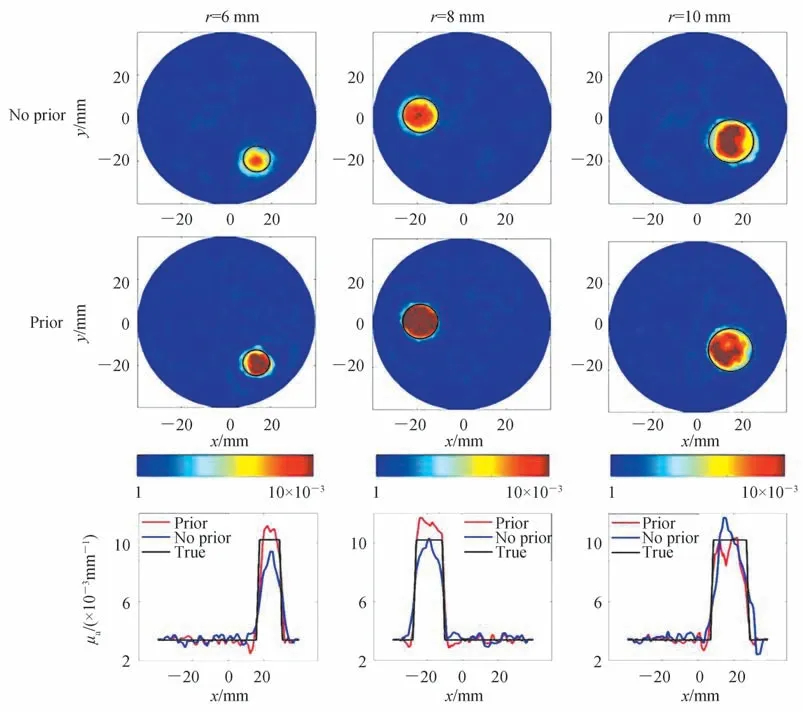
图8 不同半径下基于无先验信息和融合先验信息的圆形单异质体重建及剖线Fig.8 Reconstructed images and profiles of a single circular target with different radii based on no prior and prior methods

表2 和图9 分别是重建图像的MAE、MSE 和QR 值以及对应的条形图。进一步定量比较可以发现融合先验信息方法重建图像的MAE 在不同半径下均优于无先验信息方法的重建值，表明重建图像与真实图像差距较小。与第一种情况相同，融合先验信息方法重建图像的MSE 值没有显示出绝对优势。从QR 值可以看出，无先验信息方法的QR 值在小半径和大半径时分布显示了低估和过高估计，而融合先验信息方法的QR 值具有一定程度的过高估。综合对比发现，吸收对比度与异质体尺寸相比对重建结果影响较大，因此下文对椭圆形异质体重建图像结果评估时，仅研究了不同吸收对比度的情况。

表2 圆形单异质体相同吸收对比度不同半径重建图像评估指标计算结果Table 2 Calculation results of evaluation indexes for a single circular target reconstruction with different radii and the same absorption contrasts

图9 表2 对应的条形图Fig.9 Bar charts corresponding to Table 2

3）随机分布的单个椭圆形异质体，吸收对比度分别为1.5、2.0、2.5 和3.0。图10 是两种方法获得的重建图像以及对应的吸收系数剖线。当异质体为椭圆形时，融合先验信息方法的图像重建结果在异质体位置、尺寸、形状以及量化度方面均优于无先验信息方法的结果。尤其当吸收系数对比度较小时，无先验信息方法重建的异质体中心位置有明显的偏差且形状有明显的膨胀。在其它吸收系数对比度下，无先验信息方法重建图像存在膨胀且边缘轮廓模糊的现象。此外，从剖线图可以看出融合先验信息方法重建图像的量化度更接近真实值，而无先验信息方法重建结果在低吸收对比度和高吸收对比度时分别表现出明显的过高估和低估。

图10 不同吸收对比度下，基于无先验信息和融合先验信息的椭圆形单异质体重建及剖线Fig.10 Reconstructed images and profiles of a single elliptic target with different absorption contrasts based on no prior and prior methods

为进一步定量比较两种方法，单个椭圆异质体重建图像的MAE、MSE 和QR 值比较见表3 以及相应的条形图见图11。可以看到融合先验信息方法的三个评估指标均表现出明显的优势。以吸收系数对比度1.5为例，融合先验信息方法比无先验信息方法重建图像的MAE 和MSE 分别减少了40.1%和46.8%，且其QR值（101%）比无先验信息方法的QR 值（130%）更接近100%。其它组数据也可以观察到类似结果，即融合先验信息方法重建图像的MAE 和MSE 显著降低，并且QR 值也更接近100%。这些结果表明融合先验信息方法重建图像有更高的精度。

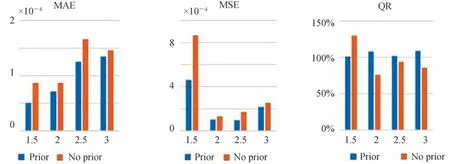
图11 表3 对应的条形图Fig.11 Bar charts corresponding to Table 3

表3 椭圆形单异质体不同目标-背景吸收系数对比度重建图像评估指标计算结果Table 3 Calculation results of evaluation indexes for a single elliptic target reconstruction with different absorption contrasts

4）随机分布的双椭圆异质体，吸收系数对比度分别为1.5、2.0、2.5 和3.0。图12 中，两种方法均可有效预测异质体的位置。比较两种方法获取的重建图像可以看到，无先验信息方法重建图像的背景伪影较多，异质体的边缘轮廓也不够清晰，且除吸收对比度为2.5 外，同一仿体中两个相同的异质体的重建结果在形状、尺寸和量化度上有明显的差异。进一步观察吸收系数剖线可以看到融合先验信息方法的剖线更接近真实值，而无先验信息方法获取的吸收系数在低吸收对比度时量化度较差，随着吸收对比度增大吸收系数有明显的过高估现象，而融合先验信息方法在不同对吸收对比度情况下均与真实值接近。

表4 为图12 各组图像的MAE、MSE 和QR 值，并绘制对应条形图13。同样以吸收系数对比度1.5 为例，融合先验信息方法重建的图像比无先验信息方法重建图像的MAE 和MSE 分别减少了34.9%和53.7%，并且QR 值分别是98%和56%，融合先验信息方法的QR 值更接近100%，表4 中的其它数据也可以观察到类似结果。总体来说，可以看出融合了先验信息使得重建图像MAE 和MSE 都显著减少，并且QR 也更加接近100%，即融合先验信息可以得到更好的重建结果。

表4 双椭圆异质体不同目标-背景吸收系数对比度重建图像评估指标计算结果Table 4 Calculation results of evaluation indexes for double elliptic targets reconstruction with different absorption contrasts

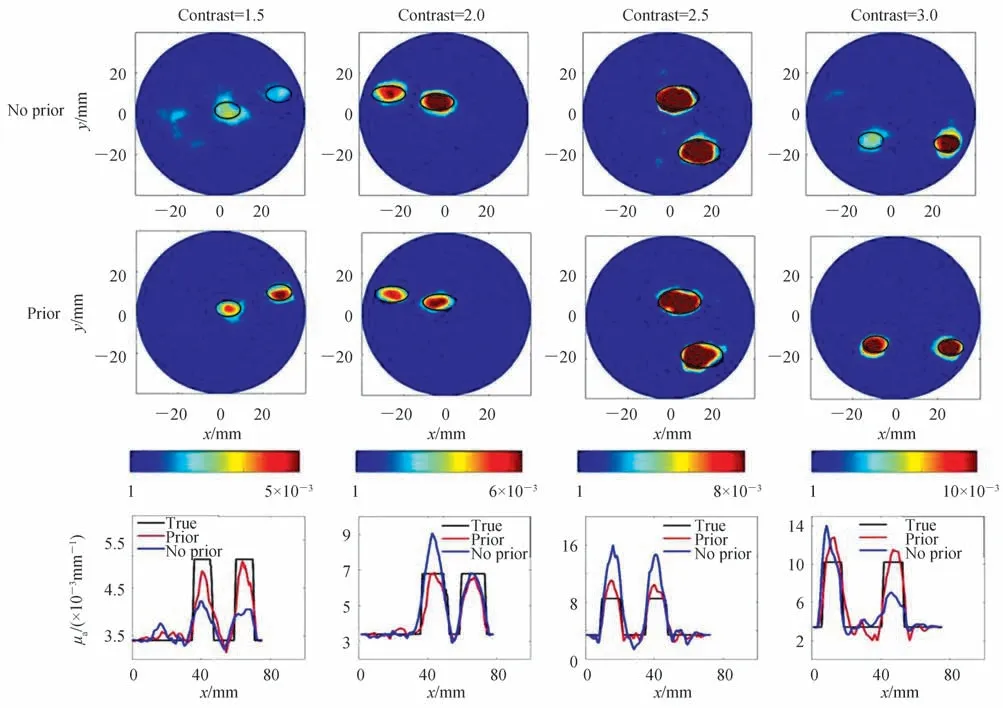
图12 不同吸收对比度下，基于无先验信息和融合先验信息的双椭圆形异质体重建及剖线Fig.12 Reconstructed images and profiles of double elliptic targets with different absorption contrasts based on no prior and prior methods

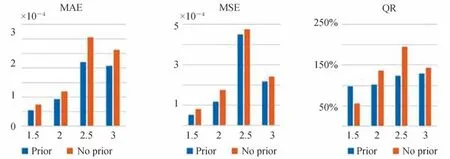
图13 表4 对应的条形图Fig.13 Bar charts corresponding to Table 4

3 结论

为了提高DOT 的重建图像质量，本文发展了一种融合先验信息SAE 神经网络方法的DOT 图像重建方法。为验证该方法的有效性，对融合先验信息与无先验信息两种方法的实验结果进行了比较和定量评估。其中，具有不同吸收对比度和不同尺寸的圆形单异质体模拟结果表明，融合先验信息方法重建结果与真实图像更接近，且当吸收对比度比较小时，融合先验信息方法对于重建图像质量改善较为明显。在异质体吸收对比度为1.5 时，与无先验信息方法相比，MAE 降低62%，MSE 降低11%，QR 由139%降低为107%，更接近100%。需要说明的是，当圆形异质体吸收对比度大于1.5 且半径较大时，理论上更容易获得异质体图像，因此两种方法均取得了较好的图像重建质量。对于包含形状欠规则的单个和两个的异质体进行图像重建，融合先验信息方法能够让背景清晰、异质体尺寸和位置准确、异质体吸收系数更接近真实值。尤其当异质体吸收系数比较小，融合先验信息可以减小预测误差。定量分析表明，融合先验信息的方法使得重建图像的MAE、MSE 都显著减小，与无先验信息方法相比MAE 至少降低8%，MSE 至少降低5%，QR 更接近100%。综合评估表明，融合先验信息能有效提高成像精度和改善重建图像的质量。