基于多角度偏振成像仪数据的测试光源变化提取方法研究
2022-02-15叶晨骆冬根李怡心姚萍萍王羿向光峰李扬李双洪津
叶晨,骆冬根,李怡心,姚萍萍,王羿,向光峰,李扬,李双,洪津
(1 中国科学院合肥物质科学研究院 安徽光学精密机械研究所,合肥 230031)
(2 中国科学技术大学,合肥 230026)
(3 中国科学院通用光学定标与表征技术重点实验室,合肥 230031)
(4 桂林电子科技大学 信息与通信学院,广西 桂林 541004)
0 引言
中国科学院安徽光学精密机械研究所研制的星载偏振传感器多角度偏振成像仪(Directional Polarimetric Camera,DPC)具有低畸变、大视场、画幅式成像的特性,使其可获得地气系统的多角度、多光谱、偏振辐射信息[1-4],将获得的偏振信息和大气特性反演模型相结合,可得到大气气溶胶和云的分布状况及相关应用参数[5-6]。DPC 载荷在出厂前,需要在实验室对DPC 响应做稳定性能测试[7-8],实验要求光源的辐射能尽可能稳定。辐射源通常采用卤钨灯积分球,周小丽等研制的近红外光源在稳定后10 min 以内光强波动约0.1%[9];袁银麟等研制的大孔径可调光谱积分球光源2 h 内的全谱段不稳定性约为0.2%[10];D'AMATO D 阐明了同一卤钨灯,其不同波段的相对光谱辐射率不同,且不稳定性也不一致[11]。光源使用年限增加导致其性能衰变,结合环境温湿度变化和操作规范性差异等因素影响,光源非稳定性[12]参数会进一步变大。因此有必要对光源进行能量监测,以降低多角度偏振成像仪的测量误差,校正稳定性测量参数[13]。本文通过对多角度偏振成像仪12 个通道的灰度值序列进行小波分解,提取出各通道的光源能量变化量并在数据处理中进行校正,以有效提升载荷稳定性参数测量精度。
1 基本原理
1.1 多角度偏振成像仪和陷阱探测器观测成像模型
搭载在某型号卫星上的DPC 在一个探测周期内可获取3 个非偏波段(763 nm、765 nm、910 nm)和3 个偏振波段(490 nm、670 nm、865 nm)共12 个通道的图像,每个偏振波段设置0°、60°、120°三个检偏方向。剩余一个本底通道用于测量DPC 的暗电流数据,以消除由于探测器自身、电路盒温度等因素造成的影响。
根据DPC 探测原理,其图像数字量(Digital Number,DN)可表示为

式中,DNDPC为像元的DN 值,GDPC为DPC 的电子增益系数,λ1、λ2为DPC 探测波段的上下限,Ls(λ)为积分球光源的光谱辐亮度,Apixel为像元面积,F为等效光圈数,Moptic为光学系统放大倍率,Tatm(λ)为环境光谱透过率,Toptic-DPC(λ)为DPC 光学系统的光谱透过率,η(λ)为探测器量子效率,tint为积分时间,Ndark为暗电流电子数总和,Nnoise1为DPC 各种噪声的总和。因此从式(1)可以看到主要影响DPC 长期稳定性的是其中4 个参数:受积分球辐亮度稳定性影响的Ls(λ)、受环境影响的Τatm(λ)、受探测器温度影响的暗电流Ndark和探测器的其它噪声Nnoise1。
陷阱探测器的探测原理可描述为

式中,s为陷阱探测器灵敏度,λ3、λ4为其探测带宽上下限,对于同一款陷阱探测器来说,λ3、λ4是固定值,MTRAP、ATRAP分别为陷阱探测器光学系统参数、探测器面积,Noffset、Nnoise2分别为陷阱探测器的固定偏置、噪声总和。因此陷阱探测器可直接测量获得光源的稳定性。
1.2 载荷非稳定性评价
载荷的一项重要指标是像元响应不确定性,即载荷非稳定性(Instability,NS),其计算公式为

式中,k为载荷在稳定性实验期间响应的总次数,y(i)为载荷第i次响应时的输出信号,为全时间段内输出信号的算术平均值。
1.3 小波分解原理
小波分解可由粗到精地对信号进行多尺度分解,所以能够很好地提取出信号中的各层低频成分[14-16],待分解信号通过低通滤波器得到低频系数A,通过高通滤波器得到高频系数D,如图1 所示,信号经第一层小波分解后得到A1和D1,然后再将第一层的低频系数A1作为第二层的输入,又得到一组低频系数A2和高频系数D2。以此类推分解,直到满足想要的频率要求。

图1 信号小波分解过程Fig.1 Signal wavelet decomposition process
待分解的原始信号可看做0 级低频系数a0=(f0,f1,...,fn),那么

式中,G为低通滤波器矩阵,H为高通滤波器矩阵,am、dm分别为当前分解m层时的低频系数、高频系数,因此

式中,G*、H*为G、H的共轭矩阵。
小波基函数为

式中,φ(t)为基小波或母小波函数,经过尺度因子a和平移因子b变换后的φa,b(t)统称小波。
对于离散信号,有

2 各观测波段光源变化量提取
2.1 实验数据的获取
以搭载在某型号卫星上的多角度偏振仪DPC 稳定性测试实验为例。其稳定性实验测试现场示意图如图2 所示,将陷阱探测器和DPC 平行放置于积分球的出光口,控制柜控制积分球的点灯数和电流,采用直径为2.5 m 的卤钨灯IS2500-1000 型积分球,工作波段是350~2 500 nm,标称全谱非稳定性为0.2%/h,所采用的SI19008 型陷阱探测器的辐射不确定度低于0.65%。先将DPC 和陷阱探测器分别正对积分球辐射源,打开积分球光源及DPC 进行预热至稳定状态,设置好相应的仪器参数,各自记录响应值,根据陷阱探测器监测的光源稳定段所对应的DPC 成像情况,经数据处理判断DPC 响应是否稳定。

图2 DPC 稳定性实验示意图Fig.2 Schematic diagram of DPC stability experiment
DPC 的同一通道在6 595 s 里采了1 024 次,采样频率为0.155 Hz,陷阱探测器监测频率是2 Hz,由Nyquist 采样定律知:DPC 各通道的DN 帧序列能检测到的最高频率是0.077 5 Hz,陷阱探测器能识别光源变化最高的频率是1 Hz。
在稳定性实验中,重点关注的是卤钨灯积分球的低频辐射变化信号[17],而陷阱探测器在监测时引入的噪声及仪器测量误差主要是相对高频噪声,因此利用小波分解可以从含有高频噪声的曲线中提取出低频的光源缓变信号。同时,在DPC 的CCD 记录数字量灰度值DN 值过程中,CCD 的光电响应的噪声较光源能量变化属于高频成分,陷阱探测器的监测灵敏度变化等噪声较光源本身的能量变化也属于高频成分,因此光源能量的低频变化曲线是暗藏在DN 值帧序列和陷阱探测器监测曲线中的。又由于陷阱探测器的采样频率比CCD 同一通道的采样频率高,因此陷阱探测器中蕴含的光源变化信息更多,但是稳定性实验只要求光源能量稳定在一定范围内,因此理论上可从DN 值帧序列中提取出光源变化趋势。
在稳定性实验中,积分球辐射源在DPC 的CCD 上所成的某一帧图像如图3 所示,由于观测位置和条件均保持不变,因此每帧的被辐射区域位置是固定的,其内接正方形尺寸约是160 pixels×160 pixels。考虑用多像元平均法提高数据信噪比,因此本次选取的像元监测区域为中央区域140 pixels×140 pixels。DPC 采用的是帧转移型面阵CCD,因此图像的预处理包括扣除当前帧及前后各3 帧本底平均和帧转移效应校正。

图3 DPC 某一通道接收到的一帧图像Fig.3 A frame of image received by one channel of DPC
2.2 光源变化曲线的提取
基于像元的光子信号和转换过程中产生的噪声变换特性,本次小波基选取的是db2 小波,分解层数为8,从陷阱探测器监测曲线中提取出光源的低频变化趋势A1~A8,也从各通道的DN 值帧曲线中提取出A1~A8,将两者之间的低频曲线做Pearson 相关,取Pearson 相关系数最大所对应的低频曲线,认为是各通道的光能量变化趋势,提取光源变化曲线流程如图4 所示。Pearson 相关系数是用来反映两变量之间相似程度的统计量,衡量两者之间的线性关联性,其对两组数据的异常值较为敏感,即数据的异常点会导致两组数据间的Pearson 相关系数降低。
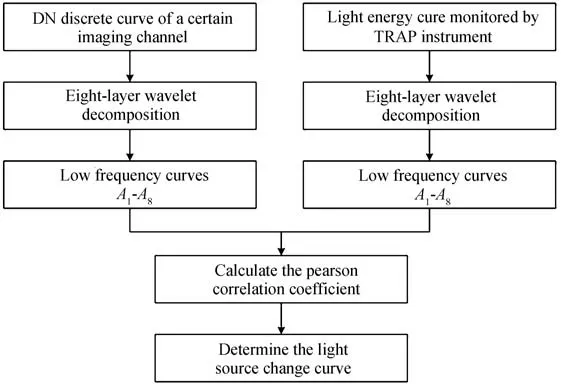
图4 提取光源变化曲线流程Fig.4 Process of extracting light source change curve
依次对12 个通道的DN 值帧曲线做8 层小波分解,将每个通道每层的低频曲线An和陷阱探测器的An计算Pearson 相关系数。以670 nm(P1)通道为例,此通道的DN 值帧曲线的A1~A8和对应陷阱探测器的A1~A8之间的Pearson 相关系数如图5 所示,DPC 的670(P1)、670(P2)、670(P3)之间的Pearson 相关系数如图6 所示。

图5 670 nm(P1)通道的DN 值帧序列的A1~A8和陷阱探测器的A1~A8的相关系数Fig.5 Correlation coefficient between A1~A8 of trap detector and A1~A8 of DPC 670 nm(P1)

图6 670 nm(P1)、670 nm(P2)、670 nm(P3)的DN 值帧序列的A1~A8之间的Pearson 相关系数Fig.6 Pearson correlation coefficient between A1~A8 of DN value frame sequence of 670 nm(P1)、670 nm(P2)、670 nm(P3)channel
由图5 可看出,对于670 nm(P1)而言,在陷阱探测器的A1~A8曲线中,Pearson 相关系数最大值均是在DN 值帧序列的A5处取得,且均在0.95 以上,说明670 nm(P1)和光源的670 nm 波段辐射能的变化极度相关。由图6 可看出670 nm 的三个偏振通道的DN 值帧序列在相同的小波分解层数下(即对角线方向),其Pearson 相关系数取得最大值,且在A5时的两两之间的Pearson 相关系数接近0.998,说明三个偏振通道的DN 值帧序列变化趋势一致,是由光源670 nm 波段的辐射能变化造成的。因此对670 nm 波段而言,其对应的DN 值帧序列的A5最能体现光源此波段的变化趋势。同理计算得到其余8 个成像通道的光源变化曲线是各自通道DN 值帧序列的A4或A5,说明在整个稳定性观测实验期间,光源的光辐射能主要以低于0.004 8 Hz的频率缓慢变化。因此,每个通道的DN 值帧序列小波分解的A4或A5即为实验期间光源变化量。
以测量的初始时刻的光能量为基准,各通道光源能量变化趋势和变化量分别如图7 和表1 所示。光源各波段的能量稳定性不一致,其中490 nm、910 nm 和865 nm 波段变化超过0.5%,因此有必要对DPC 的观测数据进行去光源变化处理,以提高稳定性参数的真实性和有效性。

图7 各通道的光源能量变化Fig.7 Variation of light source energy in all channels

表1 各波段的光能量变化Table 1 Variation of light energy in each wavelength band
利用所提取的各波段光源能量变化情况进行稳定性校正,得到利用陷阱探测器监测方法和小波分解方法前后的稳定性参数计算结果如表2 所示,可以看到两种方法获得的稳定性参数计算结果均有一定程度的提升,而小波分解方法获得的稳定性参数的提升更为明显,较好地去除了光源自身的波动、环境光谱透过率不稳定性、DPC 自身温度变化导致的暗电流不稳定性,计算出的不稳定性更接近DPC 实际工作时的不稳定性。

表2 两种校正方法的非稳定性参数计算结果对比Table 2 Comparison of calculation results of the instability parameter by two correction methods
3 基于小波分解方法提取稳定性参数的验证
3.1 实验室信噪比计算方法
1)多帧图像数据信噪比计算法
CCD 同一通道接收到了k帧图像,在被辐照区域内选取计算区域m×n,对于计算区域内的某一个像元(i,j),在k帧图像中,该像素点对应k个DN 值,求其平均值μ(i,j)及标准差std(i,j),定义该像元的信噪比为

以此类推,可求得计算区域内其它像元的信噪比。将m×n个像元的信噪比SNR(i,j)取平均,作为CCD此通道接收到的图像的信噪比SNR,即

2)相邻两帧信噪比计算法
欧洲机器视觉协会制定的图像传感器与相机性能测试标准EMVA Standard 1288[18]中提出用相邻两帧计算信噪比,取CCD 相邻两帧图像A、B,假设噪声源静止且具有均匀性,则在被辐照区域内选取计算区域m×n,定义平均灰度值即信号为

式中,yA(i,j)表示图像A中坐标(i,j)处的像元灰度值,yB(i,j)表示图像B中坐标(i,j)处的像元灰度值。
两图像A、B相减,得到新图像C,其m×n个像元灰度值的标准差记为stdC,则原图像A或B的噪声大小视为

3.2 陷阱探测器修正光源计算信噪比
在稳定性实验中,常用陷阱探测器监测光源变化曲线来对DPC 所成的图像进行去光源变化,将当前图像的建立时间与所对应的光源曲线的点对应起来,然后再去光源变化,即可计算信噪比。设某一通道的第1帧、第2 帧、...、第k帧图像建立时对应的陷阱探测器监测的光辐射能依次为Q1、Q2、...、Qk,将其光能量归一化处理,则此通道第i帧的光能量修正系数为

第i帧图像修正后的DNTRAP_corrected_i值为

将每帧图像根据陷阱探测器的光能量进行DN 值修正后,计算出的信噪比记为陷阱探测器修正后信噪比。
3.3 基于小波分解法修正光源计算信噪比
为证明提出的用小波分解法提取光源的有效性,用基于小波分解法提取出12 个成像通道各自的光源变化曲线,依据光源变化修正图像DN 值,得到修正后的帧序列信噪比以及信噪比提升比例分别见图8 和9,具体提升的信噪比数值比较见表3。由图8 可看出,小波分解法修正光源后计算出的信噪比接近相邻两帧信噪比,证明提取光源方法的正确性。

表3 陷阱探测器去光源变化法和小波分解法去光源变化法提升的信噪比数值比较Table 3 Numerical comparison of the improved SNR between trap detector de-illumination variation method and wavelet decomposition de-illumination variation method

图8 不同的方法计算的信噪比Fig.8 SNR calculated by different methods
陷阱探测器去光源修正后较未修正前信噪比平均提升了0.72%,而小波分解法修正后信噪比平均提升了2.52%。在865 nm 和910 nm 波段,小波分解去光源法将信噪比分别提升了4.34%和12.9%,远高于陷阱探测器监测数据修正的结果,反映了实验期间光源在865 nm 波段和910 nm 波段能量波动较大,也说明用宽谱的陷阱探测器监测数据来修正865 nm 和910 nm 波段的变化存在局限。在490 nm 波段,小波分解法将信噪比提升了0.54%,但陷阱探测器修正法仅将信噪比提升了0.09%,主要是因为490 nm 波段的光源能量较低,获取的图像DN 值低。虽然光源在490 nm 波段的变化最大,但信噪比提升并没有910 nm 波段显著。两种方法在670 nm 波段信噪比提升幅度小则是因为此波段的光源变化小于0.205%。

图9 陷阱探测器去光源变化法和小波分解法去光源变化法提升的信噪比Fig.9 The improved SNR of the trap detector de-illumination variation method and the wavelet decomposition deillumination variation method
4 结论
积分球光源不同光谱波段的变化趋势不同,且与光源的使用年限、环境控制、操作规范等因素有一定的相关性,但总的来说,大口径积分球光源的变化趋势较缓慢。本文提出用小波分解法从DPC 各成像通道的DN 值帧曲线中提取出光源各波段的能量变化趋势,进而扣除光源变化趋势,使稳定性测试的结果更为客观和真实。光源变化校正的效果优于传统陷阱探测器监测数据校正,DPC 的信噪比较未扣除光源波动前平均提升了2.52%,非稳定性降低到0.031%,验证了此方法提取光源变化量的有效性。
