基于拓扑栅格建模的AGV路径规划算法优化
2022-02-15徐晗,金隼,罗磊,2,刘顺
徐 晗,金 隼+,罗 磊,2,刘 顺
(1.上海交通大学 机械与动力工程学院,上海 200240; 2.上海交大智邦科技有限公司 研发部,上海 201306)
0 引 言
AGV在智能制造车间中主要应用于重物搬运、刀具更换和生产清洁等作业场景,其在具有较优路径规划能力的前提下,能够在一定程度上实现作业过程的全自动化。因此,对AGV的路径规划方法进行研究具有切实的工程应用意义,并且高效的路径规划方法也是后续研究中实现多AGV调度的关键技术基础。
目前路径规划的研究方法主要有三大类:随机采样类、图搜索类及群体智能优化类[1]。随机采样类算法具有较强的搜索能力,能够有效解决高维空间及复杂约束问题[2],但其运算成本过高,而且随机性强。图搜索类方法中比较具有代表性的是Dijkstra算法和A*算法[3],但两者都有较大的搜索量,相较Dijkstra算法而言,A*算法通过启发式搜索的方式在一定程度上提高了计算效率[4],并且成为了目前路径规划领域广泛使用的算法[5],但在地图的规划范围过大时,其计算效率依旧不高。群体智能优化类的算法则代表了当今路径规划算法的发展方向,主要有烟火、粒子群、模拟退火及遗传算法等[6],综合而言,遗传算法在处理智能制造车间中的AGV路径规划时优势明显,其计算时间少,收敛性良好,适用于求解复杂的优化问题,且鲁棒性好[7]。因此本课题将结合实际的智能制造车间作业环境,对遗传算法进行改进,完成AGV路径规划的优化。
近些年遗传算法在许多领域实现了广泛应用,但在智能制造车间中AGV路径规划的相关应用研究却较少,并且相关研究的对象主要集中于有规则布局的仓库、码头等作业环境,对于有复杂布局的智能制造车间没有高效可靠的解决方案。Nouri等[8]用调度程序代理将基于领域的遗传算法应用于移动机器人的全局搜索空间,这样能够使其动态规划更加简单,但过程消耗时间长。Zabihzadeh等[9]则提出了一种具有双信息素的遗传、蚁群混合算法,可以提高机器人的作业速度,缩短工件的转移时间,进而一定程度上解决耗时过长的问题。徐力等[10]对一种自适应的遗传算法进行了应用,该方法通过改进遗传操作算子,提出新的变异交叉自适应策略,也可以在一定程度上提高算法寻优的效率。以上研究只是针对简单作业环境应用遗传算法,并没有对模型进行有效解析进而实现高效的路径规划,本文将以此为切入点,结合拓扑建模和栅格建模,提出一种不规则布局智能制造车间的AGV路径规划方法。
1 路径规划区域模型
1.1 智能制造车间环境描述
本文以上海交大智邦科技有限公司“轿车动力总成关键零部件国产加工装备与工艺集成验证平台”的智能制造车间为研究对象,其车间环境如图1所示,AGV运动路径地图如图2所示。
该验证平台的作业AGV有3辆,分属于3个不同的作业种类:上下料AGV、抽检AGV和换产AGV。不同种类的AGV有不同的作业点位,如换产AGV的作业点位包括充电桩、夹具库、OP30、OP50、OP90、OP110、OP130,各种类AGV的作业点位之间互不冲突。此处将考虑对换产AGV的作业路径进行示例分析。从图2中可以看出,该AGV的相邻作业点位之间的距离差距较大,如Z1与Z2区中的作业点位排布紧密,而Z1与Z2区相互之间的距离以及二者与充电桩和夹具库的距离又较远,这就要求路径规划时需依据作业点位的疏密程度对不同区域应用不同的环境建模方法。

图1 轿车动力总成关键零部件国产加工装备与工艺集成验证平台
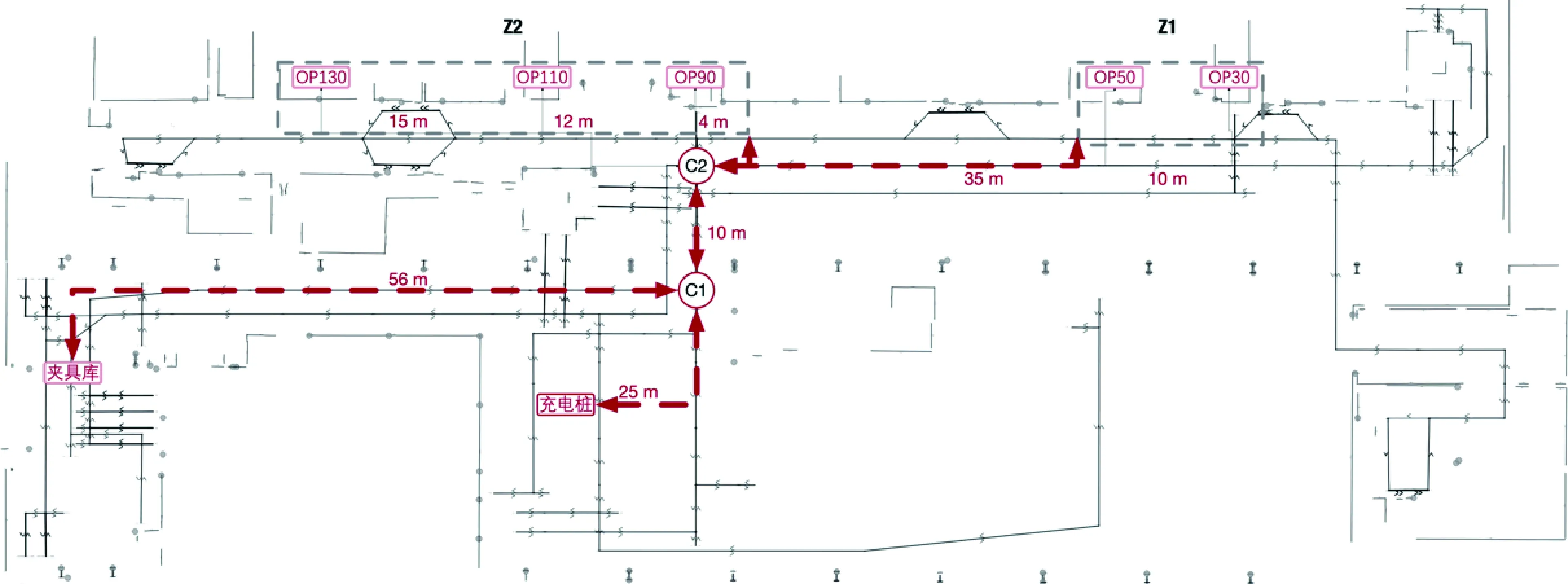
图2 AGV运动路径
1.2 模型建立
本文采用拓扑建模和栅格建模法实现环境建模。拓扑建模法是将路径交叉点和作业点位视为节点,将行驶路径视为边,通过有序的节点集合描述AGV的路径及其方向,该方法结构紧凑,尤其适用于多节点关联场景,但在如Z1或Z2区这样的作业环境下,其路径规划准确度却较低;栅格建模法是将环境离散化为基础栅格,通过对栅格的描述来获取环境信息,该方法可以对复杂作业环境进行精确细致的描述,路径规划准确度高,但其计算复杂程度高,且运算量随栅格数量的增加呈指数增加。目前的AGV路径规划建模方法都是采用单一的建模方式,但这样的建模方式并不适用于如图2所示的不规则作业车间。因此,针对不规则作业车间的环境建模需求,设计双层建模方法,首先采用拓扑建模法建立总体结构模型,然后采用栅格建模法建立作业紧密区域的描述模型,即,拓扑建模时将Z1、Z2区视为节点(图3),栅格建模时将Z1、Z2区域用栅格分解。其中,C1、C2为该AGV必经的路口节点,如图2标示。
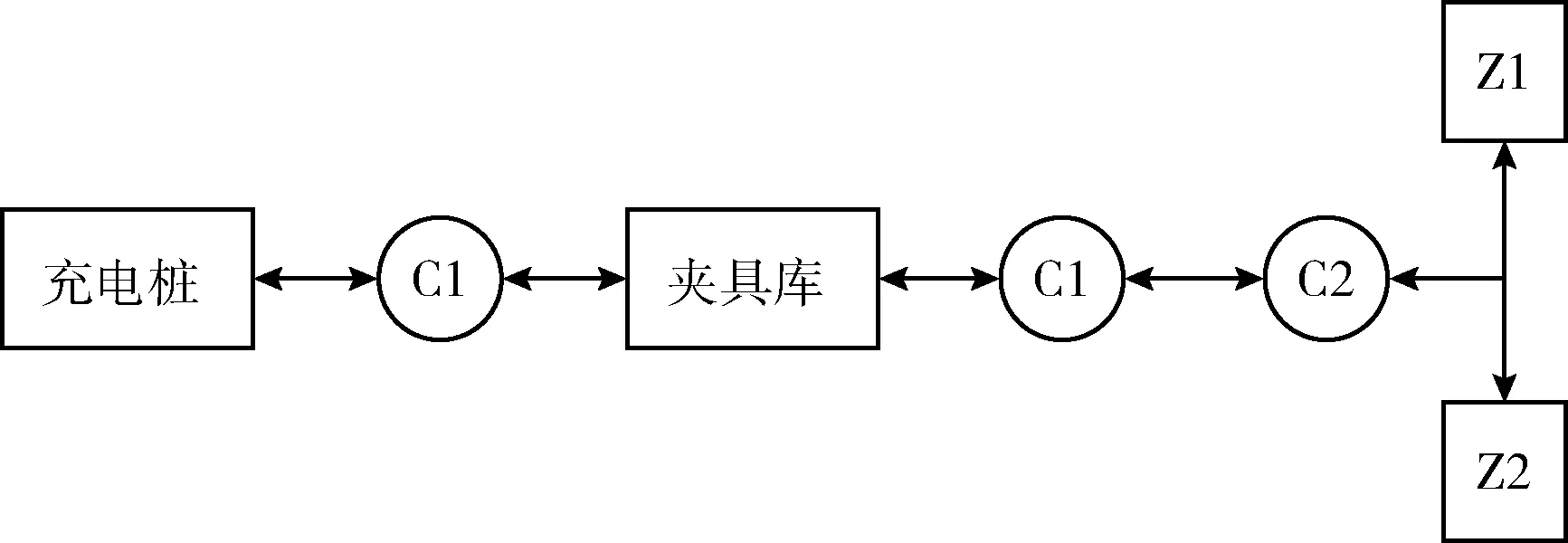
图3 换产AGV路径拓扑
在对Z1、Z2类型区域进行栅格建模时,设定栅格单元长度为AGV外形尺寸最大值,栅格地图大小为20*20,其中黑色栅格属性值为1,表示障碍物所在区域,白色栅格属性值为0,表示AGV可行区域,如图4所示。灰色栅格表示的是障碍物的膨胀区域,在实际环境中AGV不能视为质点,设置膨胀区域可以使得路径规划不经过障碍物边界。左下角和右上角栅格分别代表路径规划的起点和终点。
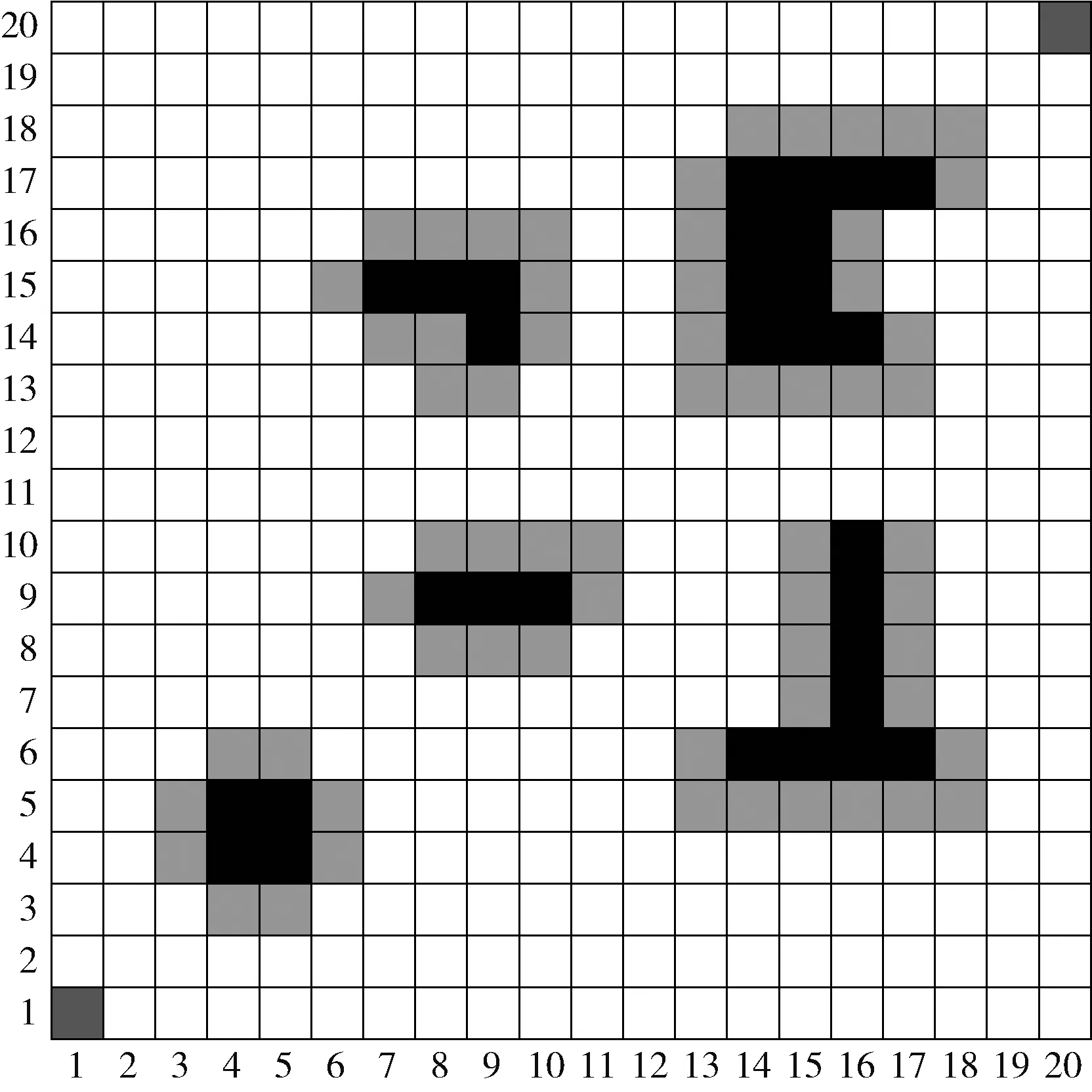
图4 区域栅格建模
以下将前文所述遗传算法应用于区域栅格环境,并在此基础上对算法进行优化。
2 区域内遗传算法应用及优化
遗传算法是一种模拟生物进化过程的计算模型,其通过模拟自然进化过程来搜索最优解。遗传算法以种群中的所有个体为对象,并利用随机化原理对一个编码后的参数空间进行高效搜索。其中,编码、初始种群设定、适应度函数设计、遗传操作、控制参数设定这5个方面是遗传算法的基本内容。基本流程如图5所示。

图5 遗传算法基本流程
2.1 编 码
在构建如图4所示的栅格地图时,需要对每一个栅格进行编码。在图4中建立直角坐系,栅格的坐标值为 {x,y}。 对每一行中的栅格从左到右进行编码,并逐行从下到上进行编码,编码方式为十进制。栅格坐标与编号的转换公式为
(1)
其中,N为栅格的十进制编码值,起始值为0,Sraw为每一行的栅格数量,[x]为高斯取整函数,%表示取余数函数。
2.2 种群初始化
路径规划的种群初始化就是按一定规则生成多条初始路径,并判断各路径的连续性,并将间断的路径连接成连续的路径。路径的起点和终点分别设定为AGV的起始点和目标点,并在每一行中随机选取一个栅格,构成路径节点集合,按照图6所示种群初始化流程完成路径的初始化。

图6 路径种群初始化流程
其中,栅格j与栅格j+1是否连续的判别方法为
d=max{|xj+1-xj|,|yj+1-yj|}
(2)
当d=1时,栅格j和栅格j+1连续,否则不连续。
在对两个不连续栅格选取中间栅格时,其坐标的计算方法为
(3)
2.3 适应度函数设计
适应度函数是衡量种群质量的唯一标准,适应度函数的设定取决于系统要优化什么样的目标。在AGV的路径规划中,通常需要优化的首要目标就是路径的长度。在传统的路径规划遗传算法中,适应度函数的表达式为[7]
(4)
其中,ng为所通过的栅格数,D为路径的总长度,表达式为
(5)
通过f0衡量种群个体的适应度可以淘汰路径长度较大的个体,但这种传统适应度函数的问题在于,其并未结合AGV的实际运动过程来考虑路径的平滑度。在实际的运动过程中,如果AGV转向次数过多,不仅会增加运动时间,还会造成车辆机械结构的快速磨损,其运动的累积误差也会随转向次数的增多而增大,因此这里需要对生成路径的平滑度(非数学意义上的平滑)进行考量。
根据三角形的几何关系,相邻三点之间的距离关系可以表征路径的平滑度。3个相邻栅格之间的距离表达式如下
(6)
(7)
(8)
(9)
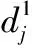
(10)
综合考虑路径的长度以及平滑度,改进后的适应度函数表达式如下
f=f0+f1
(11)
2.4 遗传操作
2.4.1 选择
传统遗传算法中通常采用轮盘赌的方式来选择个体,即计算个体适应度占总体的适应度和的比例[7]
(12)
此方法虽然简单有效,但极易使算法陷入局部最优。通过对照模拟退火算法的特性,本课题考虑使用其来对种群进行选择。模拟退火算法思路来源于晶体冷却过程:从某一较高的初温出发,伴随着温度的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。由于此处的最优解应为适应度最大值,故应对所有f(x)进行相反数化,因此适用于此处的模拟退火的接受概率公式为[11]
(13)
Δf=f(x0)-f(x)
(14)
(15)
其中,f(x0)、f(x) 分别为进化前后的适应度函数值;T为当前的温度值;T0为系统初始温度;α为系统温度衰减率,为确保有较大搜索空间,通常取0.7≤α≤1.0;k为迭代次数;M为待反演参数的个数,通常取1。
模拟退火方法进行种群选择的流程如图7所示。

图7 模拟退火种群选择流程
2.4.2 交叉
交叉操作是指两个个体之间的片段交换。将每一个个体(路径)视为一条染色体,将每一个个体中的栅格节点看作染色体上的基因,交叉操作就是要找出两条染色体上相同的基因,随机选取其中一个,将此基因之后的片段相互进行交换。
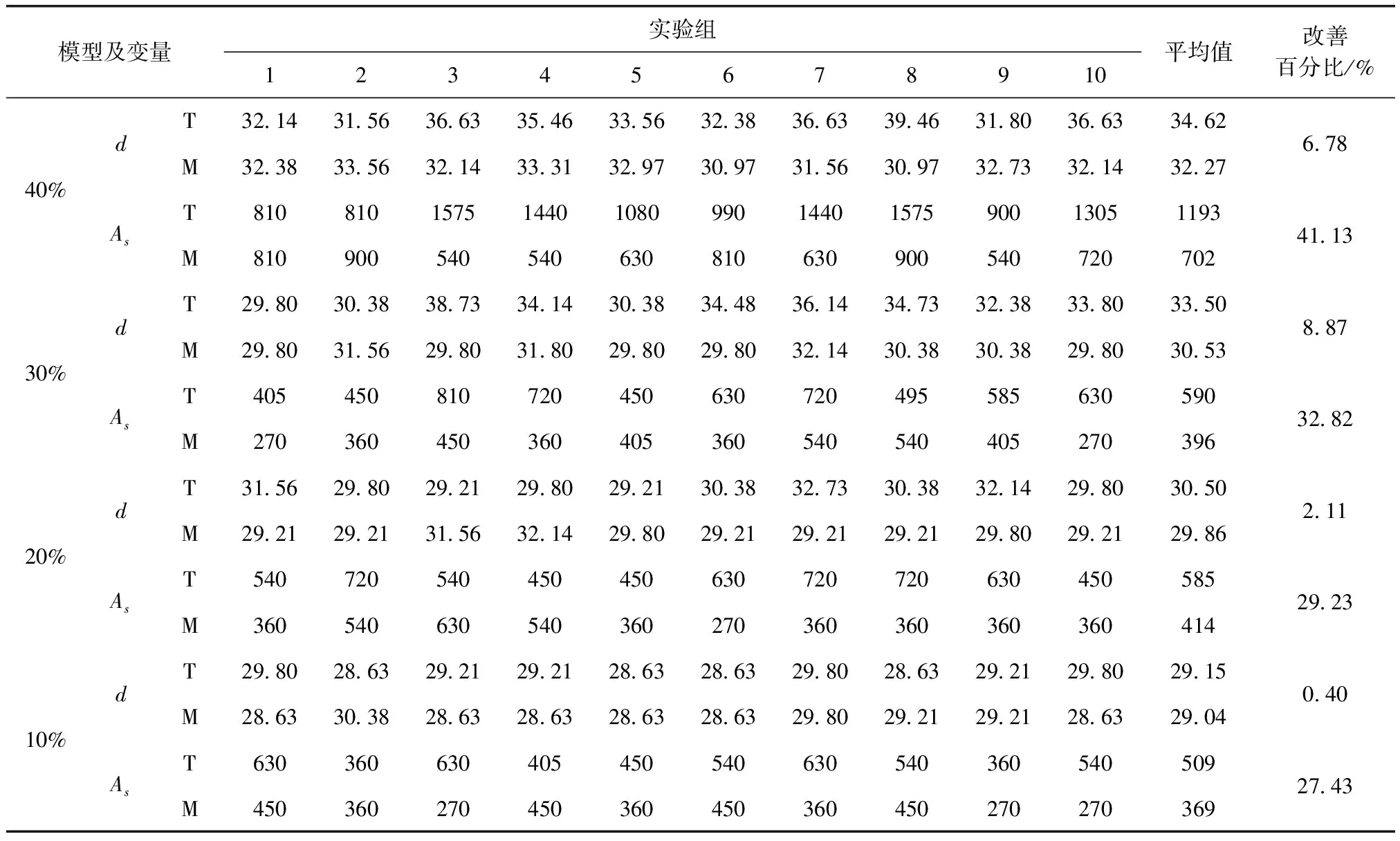
设定交叉概率Pc,并随机产生一个0-1之间的数Rc,将其与Pc比较,若Rc 2.4.3 变异 变异操作通过重新设定染色体中的片段,保证了种群的多样性。变异操作需要随机选取染色体(路径)中除起点和终点外的两个基因节点,并去除这两个节点中间的栅格,利用前述种群初始化中路径连续化的方法,生成连续的路径片段。 设定变异概率Pm,并随机产生一个0-1之间的数Rm,将其与Pm比较,若Rm 本节通过对上述区域内改进算法进行编程,并基于MATLAB R2018a平台对算法的有效性进行仿真实验验证。本节将对改进后的适应度函数和种群选择方法进行分别验证,并考虑障碍物在栅格空间中的不同占比大小对算法有效性的影响。 由2.3节中式(4)~式(11)可知,f0是系统优化目标只考虑路径长度的适应度函数,而f是优化目标考虑路径长度以及路径平滑度的适应度函数。本小节将对f0和f进行仿真实验对比研究,以此来验证附加考虑路径平滑度的适应度函数设计是否有效。 在对适应度函数进行验证时,种群选择的方式选用式(12)轮盘赌方法。系统参数设定如下:地图栅格总数为400,种群数量Np为200,遗传算法的进化代数为70,交叉概率Pc为0.8,变异概率Pm为0.2。 分别对适应度函数为f0和f的模型进行计算,其AGV运动路径如图8和图9所示。对两种模型分别计算10组,得出每一个实验组的最优路径长度和两种适应度函数模型各自的平均值,以及各实验组AGV转向角度的绝对值之和和两种模型各自的平均值,见表1。 图8 适应度函数为f0的AGV运动路径 图9 适应度函数为f的AGV运动路径 两条路径对比可以看出,适应度函数为f0的运动路径转向次数较适应度函数为f的多,且根据表1可知,平均地,应用f的模型转向角度绝对值之和相较于传统模型少26%,这对于重型搬运AGV有显著的积极影响。进一步地,通过对两种模型路径长度平均值的对比,发现对路径平滑度进行附加考虑并不影响路径的长度。由此可见,改进后的适应度函数应用于复杂作业环境中是十分有效的。 本小节将基于适应度函数为f的模型对模拟退火种群选择法和传统轮盘赌选择法进行比较验证。 模拟退火参数设定如下:系统初始温度T0为10 000 K;为了保证有较大的搜索空间,系统温度衰减率α设为0.9;依据式(15),设定系统最终温度为1 K,则迭代次数为87次。 对使用模拟退火选择法的模型进行计算,其AGV运动路径如图10所示,图11表征了每一代解的平均值与最优解的收敛关系。对该模型分别计算10组,得出每一个实验组的最优路径长度和样本总体的平均值与方差,见表2。 表1 应用两种模型的多实验组路径长度与转向角度对比 图10 模拟退火选择法模型的运动路径 从图10和表2中多组实验数据可知,模拟退火法选择出的路径平滑,且路径长度也较短,更为核心的是,应用模拟退火选择法的模型在多数情况下都能搜索到系统的最短路径(29.80),且总体方差小,而应用轮盘赌选择法的模型却十分容易陷入局部最优而得不到全局最优解。仿真实验结果表明,应用模拟退火种群选择法的模型有效避免了传统遗传算法易陷入局部最优的缺陷。 图11 路径长度优化曲线 本小节将对改进算法在不同障碍物空间中的有效性进行仿真实验分析。 表2 两种选择法多实验组路径长度 在对不同障碍物占比的栅格环境进行设置时,发现当障碍物栅格占比接近50%时,传统的遗传算法和改进后的遗传算法都难以解算出最优解,其可行路径只有两条,即图12中的虚线和点线。由于该算法采用的栅格连续化方法(图6),当空间障碍物过多时,通过随机方法选取的栅格之间难以形成连续的无障碍物的不间断路径,因此生成的路径被不断舍弃,使得程序极易陷入死锁而无法解算出最优路径。因此,当障碍物栅格占比接近或超过50%时,该算法就失去了有效性。 以下将对不同障碍物栅格占比分别为10%、20%、30%、40%的环境进行解算分析,其障碍物布置如图13所示。通过设置不同的障碍物环境,并对不同模型各进行10组仿真实验,各实验组的最优路径长度和AGV转向角度绝对值之和见表3。其中,d为模型解算出的最优路径长度,As为最优路径的AGV转向角度绝对值之和,T表示传统遗传算法模型,M表示改进后的算法模型。 图12 障碍物栅格占比为50%的解算路径 图13 不同障碍物栅格占比 从表3中的数据对比可以发现,对于最优路径长度和最少转向度数两个优化目标,改进后的算法在障碍物栅格占比越多的空间中越有效。在障碍物少、环境较为简单的空间中,模型对路径平滑度的考量表现出了良好的优越性,但模型采用的模拟退火方法却失去了优越性,可能原因是当障碍物较少时,种群生成的初始路径趋于连续化、同质化,因此传统的轮盘赌选择方法也能大概率搜索到最优解。 由上述仿真实验验证得出,对不同障碍物栅格占比的环境来说,改进后的复杂子区域路径规划算法的有效区间为障碍物占比小于等于40%,在此范围内,障碍物占比越高,算法有效性越好。 在对Z1、Z2类型复杂子区域完成路径规划后,需要依照图3对AGV的全区域路径进行规划。其实根据图2可以看出,图3各拓扑节点之间路径平直,且无障碍物,在这种情况下,将节点之间的AGV运动路径固定是最为简单有效的方法,固定路径的具体设置由工程师根据工厂的环境进行判断,对于图2的环境,其固定路径如图中粗虚线所示。 预设的固定路径行驶可以通过简单运动控制来实现。AGV通过里程计来获取运动的里程信息和转向角度信息,里程计信息来源于车身驱动轮光电编码器和惯性测量单元记录的相对位姿变化。在此基础上,AGV的激光雷达实时测量其与车间固定参照物(如贴在墙体上的激光反射条,图14)的距离,由此解算出AGV的实时位置姿态信息,进而实现固定路径行驶。 因此,当AGV行驶在非复杂环境路段时,采用预设固定路径的方法简单高效,避免了全局栅格建模计算资源占用,系统反应慢的问题。 表3 各模型路径长度及转向角度对比 图14 激光反射条 研究基于不规则布局的智能制造车间,提出了一种拓扑栅格混合建模的方法,并对复杂子区域的路径规划算法进行了优化改进。 (1)对整个AGV运动区域进行拓扑建模,视复杂子区域为节点,对节点间的路径规划采用预设固定路径的方法。 (2)对复杂子区域进行栅格建模,模拟多障碍物的环境,应用遗传算法对路径进行规划。 (3)改进了传统遗传算法的适应度函数,综合考虑路径长度和平滑度(非数学意义上的平滑)对路径规划的影响,有效改良了路径的平滑度;提出了不同于传统种群选择方法的模拟退火种群选择法,有效避免了传统方法易陷入局部最优的缺陷,并通过MATLAB仿真实验完成了验证。 (4)仿真实验验证了改进算法的有效性区间,当障碍物栅格占全环境比小于等于40%时,算法有效,且在此范围内,障碍物占比越高,其有效性越好。 对于实际的智能制造车间,改进后的路径规划方法可以应用到车间AGV调度系统中,并结合一定的调度策略,实现多台AGV的有效调度。3 区域内改进遗传算法仿真实验
3.1 改进适应度函数有效性验证
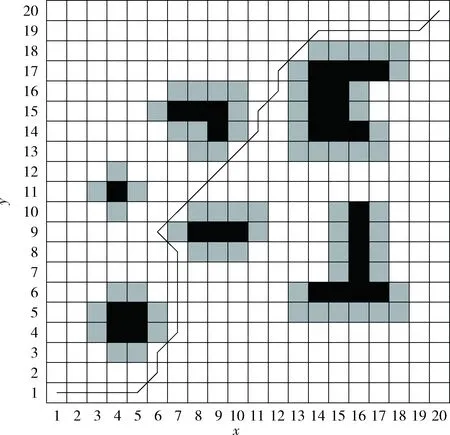
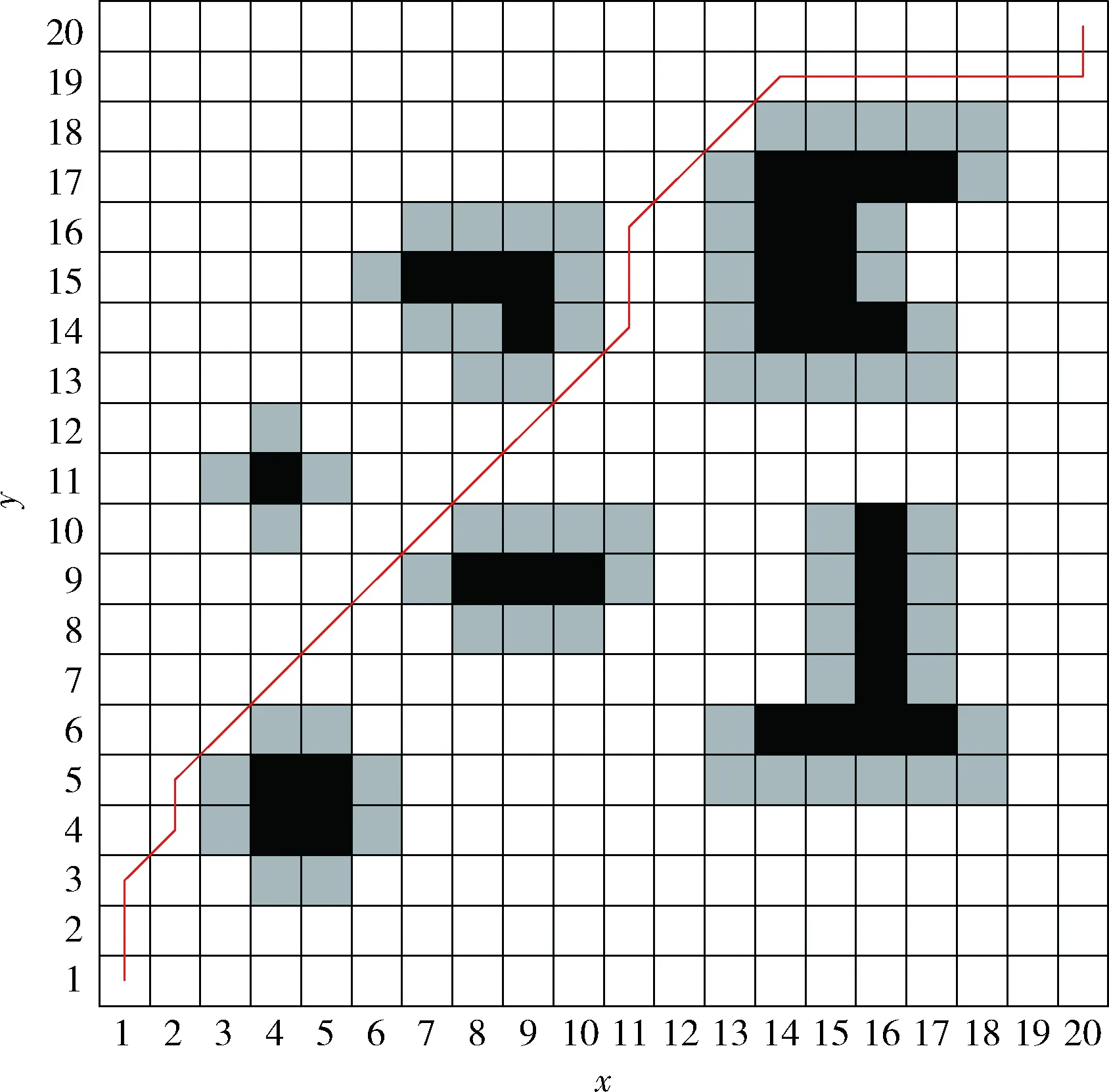
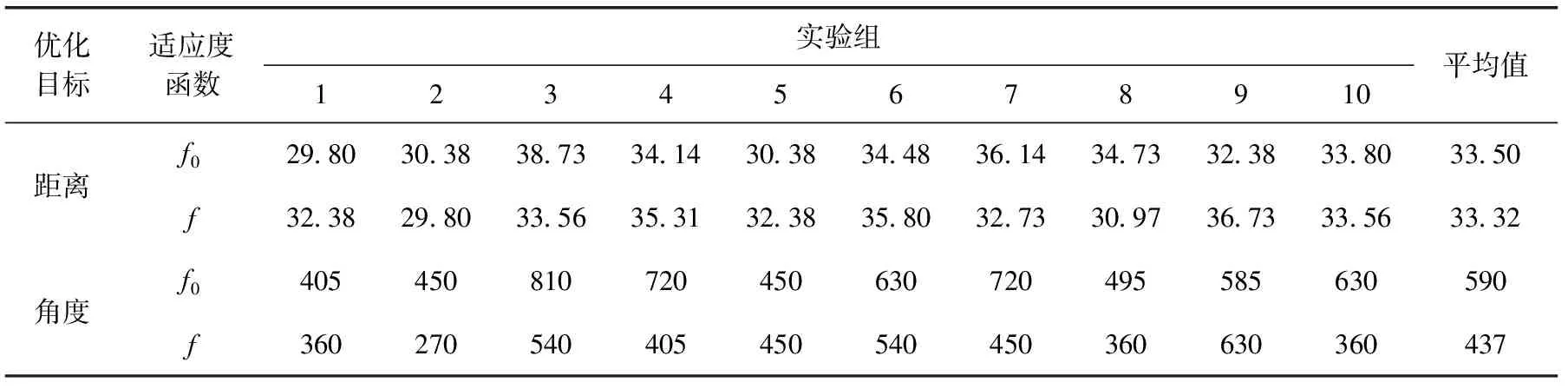
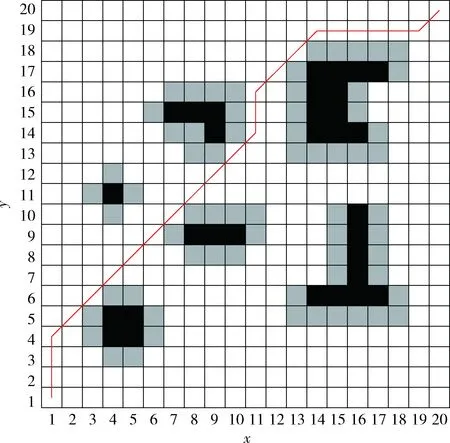
3.2 模拟退火选择法有效性验证

3.3 障碍物数量对算法有效性的影响



4 拓扑节点间路径规划方法

5 结束语
