基于冲击载荷的硬质合金球齿碎岩机理研究
2022-02-15陈宝义曹宏宇曹金娥崔国庆
杨 达,陈宝义,曹宏宇,曹金娥,崔国庆
(吉林大学建设工程学院,吉林长春130026)
0 引言
在滑坡防治大直径桩孔施工过程中,快速钻进是治理成功的关键。而气动潜孔锤因钻进效率快等优点被广泛应用于滑坡防治施工中[1-3]。
气动潜孔锤工作原理是高压气体交替进入钻具前后气室,形成压力差,推动活塞往复运动冲击钻头[4-7]。在冲击过程中,应力波传递到钻头表面球齿,作用于岩石并将岩石破碎。相邻球齿产生的破碎坑相互干涉,通过钻头回转,球齿切削破碎坑之间的岩石,使岩石表面完全破碎,因此钻头表面布齿和合理冲击功是影响钻头碎岩性能的关键因素。潜孔锤钻头的合理布齿,即确定钻头上最少的齿数和最佳的布齿位置,有利于提高碎岩效率与降低破碎比功。潜孔锤钻头底面布齿以单个球齿碎岩机理的研究结果为理论依据,得出单个球齿冲击产生的破碎坑大小,按球齿之间破碎坑连接且无岩缝的要求,计算每圈布齿个数与大小,从而对钻头布齿进行优化设计[8-13]。钻头布齿以单个球齿冲击岩石后的破碎坑直径为布齿依据之一,因此对球齿在不同冲击功情况下破碎岩石,观察岩石破碎情况的研究,具有重要意义:朴金石[14]分析压头以不同冲击功侵入花岗岩与安山岩时坑宽与深的比值;任红[15]、Chen 等[16]对不同冲击功条件下2 个球齿压入岩石产生的应力云图及破碎情况进行分析。在球齿冲击岩石时,探究碎岩机理,对研究岩石破碎情况具有重要意义:彭伟等[17]对不同柱齿所适用的岩层进行分析,得出球齿在钻进硬岩地层时,可保证具有较高的钻进效率和较高的耐磨性,并基于球齿的碎岩机理[18],同时考虑相邻球齿侵入岩石的相互作用,确定布齿的最优间距。M.P. Mavlutov 对Ø19.5 mm 的压头做自由落体冲击大理石试验[19],得出:岩石受到冲击功较小时,表面产生微小裂纹带,但当冲击功增大到第1 次临界值时,岩石发生第1 次破碎,随着冲击功继续增大,压头侵入深度也随之增大,当冲击功增大到第2 次临界值时,岩石发生第2 次破碎。之后重复上述过程,侵入深度继续增加,直到冲击功增大到第3 次极大值时,岩石发生第3 次破碎并继续循环。李从保等[20]、方金[21]、Jiang 等[22]、Deng 等[23]、Saadati等[24]、LIU 等[25]通过数值模拟软件建立球齿冲击岩石模型,进行球齿碎岩数值模拟,得出在岩石在受到冲击载荷作用下,应力以应力波形式向岩石各个方向传递,球齿钻进时易对两侧岩石产生拉裂破坏。通过数值模拟分析,发现持续冲击导致岩石内部失稳,并逐步衍生出裂纹。当裂纹发育到一定程度,岩石发生完全破碎。朱丽红等[26]采用ANSYS 分析研究球齿碎岩机理,通过模拟结果得出球齿冲击碎岩包括压碎和剪崩2 部分。当球齿与岩石接触瞬间,球齿下方的岩石形成半球形弹性区。球齿继续移动,应力波以岩石与球齿接触点为中心,呈半球形向岩石内部传播,当球齿对岩石产生的侧压力增大到临界值时,岩石崩离,形成破碎坑。
冲锤通过钻头-球齿将冲击功传递到岩石后,岩石根据冲击产生的应力波发生破碎。李夕兵等[19,27]采用一维应力波对岩石进行冲击实验的方法,从破碎能量消耗与力学性质2 方面对岩石受到的冲击载荷进行研究,得出当入射应力波大于岩石破碎的临界应力值且应力波持续冲击时间大于岩石破碎失稳所需时间时,岩石发生破碎。岩石破碎的效果取决于应力波的大小与持续时间。
彭伟、M.P.Mavlutov 从宏观方面描述了球齿与压头在冲击碎岩过程中岩石的破碎情况与碎岩机理,李从保、方金等通过采用数值模拟软件模拟球齿冲击岩石破碎,得出应力波在岩石中的分布情况,但却未针对球齿在冲击破碎岩石后产生的破碎坑大小与产生的应力波传递情况对岩石破碎机理的影响进行分析。因此本文结合实验与模拟,对岩石受到球齿冲击后所产生的破碎坑面积以及应力波对岩石破碎机理的影响进行研究分析。
根据岩石破碎理论以及现场施工状况,最优冲击功与合理布齿对于提高碎岩与救援效率具有关键作用。然而由于钻头表面球齿数量多,钻头模型大且相邻球齿碎岩时相互影响等问题,分析较为复杂。因此,本文通过ABAQUS 显示动态分析数值模拟研究不同冲击功对单个球齿碎岩的影响,同时观察应力波的传递、岩石破碎面积与破碎比功来研究岩石破碎规律。本文以特大滑坡应急处置与快速治理项目中的Ø600 mm 潜孔锤钻头所配用的球齿为样本进行分析。
1 球齿冲击碎岩数值模拟
1.1 有限元模型的建立
Ø600 mm 潜孔锤所用球齿直径19 mm,高30 mm。为保证模拟的准确性并提高运算效率,本文采用平面二维模型进行分析,依据冲击峰值压力引导的应力分布,可确定岩石尺寸设计为球齿直径的5~7 倍[28],即 140 mm×100 mm。将岩石下底面进行X、Y方向完全固定约束。球齿刚体约束,沿中心轴运动。模型网格按楔形进行划分,并对球齿侵入岩石接触点周围加密处理,其余部位采用整体网格划 分 。 在 网 格 之 间 插 入 0 厚 度 的 Cohesive 单元[29-30],该设置不影响计算结果,使破碎容易产生并且纹随机扩展合理。岩石网格类型采用平面应变CPS3;Cohesive 网格类型采用粘性COH2D4。球齿单次冲击模型网格划分见图1,10 个球齿依次进行冲击模型网格划分见图2。模型共划分为134442 和139293 个网格。

图1 球齿单次冲击模型网格划分Fig.1 Meshing of the spherical tooth single impact model

图2 10 个球齿冲击模型网格划分Fig.2 Meshing of the spherical tooth 10 time impact model
岩石与硬质合金球齿主要物理属性见表 1[31-32]。

表1 岩石与球齿参数Table 1 Parameters of rock and carbide spherical teeth
为探究冲击功大小与碎岩效果的影响,将冲击功分为 5 组,分别为 20、25、30、35、40 J,并依次对 5组冲击功进行模拟。
1.2 材料的损伤演化与单元删除
图3 所示为承受损伤的岩石材料特征应力-应变行为。在具有各向同性硬化的弹塑性材料中,损伤以2 种方式得以体现:屈服应力的软化和弹性的退化。图中的实线代表受损伤的应力-应变曲线,而虚线是没有损伤的曲线。损伤取决于单元的特征尺寸,这样便可使结果的网格相关性最小化。

图3 具有渐进性损伤退化的应力-应变曲线Fig.3 A stress-strain curve with progressive damage degradation
在图 3 中,σy0和是损伤发生时的屈服应力和等塑性应变;当时网格失效 ,即整体损伤变量达到D=1 时的等塑性应变。整体损伤变量D捕捉所有有效失效机理的组合影响,并以计算单个损伤变量di的形式σy0得到。等塑性应变在失效时的值取决于单元的特征长度,并对于损伤演化规律以等效塑性位移的形式来制定。

式中:L——单元的特征长度,如果将失效时的塑性位移指定为0,则发生即时失效;或者以断裂能耗散Gf的形式来指定,如果指定Gf=0,则失效将立即发生。
1.3 岩石破碎理论依据
目前尚无成熟的理论与测试方法准确确定钻头与岩石的碰撞作用时间,因此采用破碎比功,即破碎单位面积所用冲击功As[33]来表示冲击效率具有实际意义,破碎比功As可表示为:

式中:A——花岗岩破碎面积,mm2,实验中的破碎面积采用游标卡尺测量破碎坑的直径D1、D2(见图4),由于球齿顶面为半球形,因此破碎面积按照Ae=π×[(D1+D2)/4]2进行计算,模拟中为二维模型,测量破碎坑直径为D3(见图4),破碎面积按照Am= π×(D3/2)2;W——冲击功,J。

图4 破碎坑直径测量Fig.4 Diameter measurement of the crushed pit
2 单齿碎岩实验研究
2.1 实验方案
设计冲锤自由落体实验台如图5 所示。实验岩样为290 mm×250 mm×150 mm 的花岗岩。实验台底面采用2 层结构进行固定,上部平台设立1 根滑轨,将滑块放置在滑轨上,钻头连接滑块上的连接板,通过电磁铁连接钻头上部连接板,断电后电磁铁失去吸力,使钻头进行自由落体运动,冲击岩石。单次冲击完成后将冲锤固定到原位置再次冲击,进行重复冲击碎岩实验。在每次冲击后,清除岩粉,记录破碎坑直径,计算岩石破碎面积。

图5 单齿碎岩实验台Fig.5 Single tooth rock crushing test bench
下落高度根据公式(2)与公式(3)推出:

式中:h——下落高度,m;W——冲击功,J;M——钻头质量,11.8 kg;V——冲击末速度,m/s。
冲击功与下落高度的关系见表2。

表2 冲击功与下落高度Table 2 Impact energy and falling height
2.2 实验与模拟对比分析
2.2.1 20 J 冲击功冲击效果
当球齿冲击功为20 J 时的冲击效果见图6,在初始时刻岩石的von-mises 应力范围主要在8.33~66.67 MPa 之间,最大应力为86.96 MPa。根据图6(a)可知在球齿初始冲击岩石时,岩石发生弹性变形,此时的应力波呈半球形扩散,主要分为8.33~16.67、16.67~25、25~69.6 MPa 3 个应力区,且中间的应力明显高于两侧,随着进一步冲击,球齿与岩石接触点下方的应力超过岩石的抗拉强度10.2 MPa,因此容易在中间产生裂缝,形成压裂的效果,且接触点两侧随着球齿侵入产生破碎,如图6(b)所示,当球齿完成一次冲击后,如图6(c)所示,岩石形成破碎坑,面积达到最大为20.2107 mm2。

图6 20 J 岩石破碎与von-mises 应力变化Fig.6 Rock fragmentation and von-mises stress variation at 20J
2.2.2 25 J 冲击功冲击效果
当球齿冲击功为25 J 时的冲击效果见图7,在初始时刻岩石的von-mises 应力范围主要在8.33~66.67 MPa 之间,最大应力为86.96 MPa。根据图7(a)可知在球齿初始冲击岩石时,岩石发生弹性变形,此时的应力波呈半球形扩散,主要分为8.33~16.67、16.67~25、25~69.6 MPa 3 个应力区,且中间的应力明显高于两侧,随着进一步冲击,接触点下方的应力达到岩石的抗拉强度10.2 MPa,因此容易在中间产生裂缝,形成压裂的效果,从图7(a)可知球齿与岩石接触点左侧应力主要在25~41.67 MPa 之间,大于右侧的8.33~25 MPa,且在应力波传递过程中对岩石会产生拉应力,因此在冲击过程中,球齿左侧优先产生压裂,如图7(b)所示,当球齿完成一次冲击后,如图7(c)所示,岩石形成破碎坑,由于冲击功增大导致接触点下方应力主要为50 MPa,且接触点左侧应力也增大,导致岩石破碎面积突变,最大面积为40.0091 mm2。
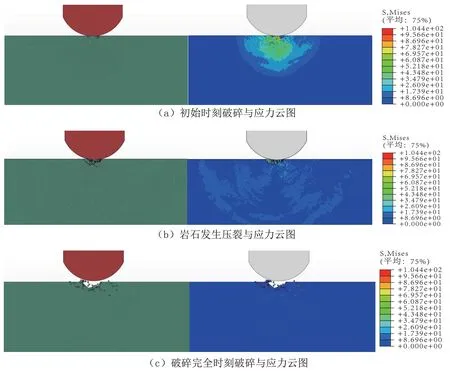
图7 25 J 岩石破碎与von-mises 应力变化Fig.7 Rock fragmentation and von-mises stress variation at 25 J
2.2.3 30 J 冲击功冲击效果
当球齿冲击功为30 J 时的冲击效果见图8,在初始时刻岩石的von-mises 应力范围主要在8.33~66.67 MPa 之间,最大应力为86.96 MPa。根据图8(a)可知在球齿初始冲击岩石时,岩石发生弹性变形,此时的应力波呈半球形扩散,主要分为8.33~16.67、16.67~25、25~69.6 MPa 3 个应力区,且中间的应力明显高于两侧,随着进一步冲击,接触点下方的应力达到岩石的抗拉强度10.2 MPa,因此容易在中间产生裂缝,形成压裂的效果,从图8(a)可知球齿与岩石接触点左侧应力主要在25~41.67 MPa 之间,大于右侧的8.33~25 MPa,且在应力波传递过程中对岩石会产生拉应力,因此在冲击过程中,球齿左侧优先产生压裂,如图8(b)所示,当球齿完成一次冲击后,如图8(c)所示,此时岩石形成破碎坑,面积为40.1968 mm2。

图8 30 J 岩石破碎与von-mises 应力变化Fig.8 Rock fragmentation and von-mises stress variation at 30J
2.2.4 35 J 冲击功冲击效果
当球齿冲击功为35 J 时的冲击效果见图9,在初始时刻岩石的von-mises 应力范围主要在8.33~66.67 MPa 之间,最大应力为95.66 MPa。根据图9(a)可知在球齿初始冲击岩石时,岩石发生弹性变形,此时的应力波呈半球形扩散,主要分为8.33~16.67、16.67~25、25~69.6 MPa 3 个应力区,且中间的应力明显高于两侧,随着进一步冲击,接触点下方的应力达到岩石的抗拉强度10.2 MPa,因此容易在中间产生裂缝,形成压裂的效果,从图9(a)可知球齿与岩石接触点左侧应力主要在25~41.67 MPa 之间且大于右侧,且在应力波传递过程中对岩石会产生拉应力,因此在冲击过程中,球齿左侧优先产生压裂,如图9(b)所示,当球齿完成一次冲击后,如图9(c)所示,应力波转化为岩石内能消失,岩石形成破碎坑,此时接触点下方应力为25~41.67 MPa 区域相较于30 J 冲击功时扩大,且接触点右侧应力也随之变大,岩石更容易破碎,因此岩石破碎坑面积发生第二次突变,为52.8858 mm2。

图9 35 J 岩石破碎与von-mises 应力变化Fig.9 Rock fragmentation and von-mises stress variation at 35J
2.2.5 40 J 冲击功冲击效果
当球齿冲击功为40 J 时的冲击效果见图10,在初始时刻岩石的von-mises 应力范围主要在8.33~66.67 MPa 之间,最大应力为95.66 MPa。根据图10(a)可知,在球齿初始冲击岩石时,岩石发生弹性变形,此时的应力波呈半球形扩散,主要分为8.33~16.67、16.67~25、25~69.6 MPa 3 个应力区,且中间的应力明显高于两侧,随着进一步冲击,接触点下方的应力达到岩石的抗拉强度10.2 MPa,因此容易在中间产生裂缝,形成压裂的效果,从图10(a)可知球齿与岩石接触点左侧应力主要在25~41.67 MPa 之间且大于右侧,且在应力波传递过程中对岩石会产生拉应力,因此在冲击过程中,球齿左侧优先产生压裂,如图10(b)所示,当球齿完成一次冲击后,如图10(c)所示,岩石形成破碎坑,此时破碎面积为52.8858 mm2,但随着应力波扩散,在破碎坑两侧的岩石表面应力未达到岩石的抗拉强度与抗剪强度,因此破碎面积不再扩大,与冲击功为35 J 时破碎面积一致。

图10 40 J 岩石破碎与von-mises 应力变化Fig.10 Rock fragmentation and von-mises stress variation at 40J
模拟过程中球齿冲击岩石后,产生反弹,向初始方向的反方向运动,因此岩石在破碎后,不会因球齿反弹造成再次冲击岩石导致二次破碎。
2.3 实验与模拟结果分析
本文采用实验与模拟方法,得出岩石在5 组冲击功情况下冲击10 次后产生的破碎面积与破碎比功对比关系。
图11 为破碎面积对比曲线。当实验冲击功为20 J 时,岩石破碎面积最小,且随着冲击功的增大而增大,但当冲击功为30 J 时,岩石破碎面积明显高于25 J 与 35 J,但低于 40 J。模拟冲击功为 20 J 时,10次冲击后岩石破碎面积与实验一致;冲击功为30 J与25 J 时,10 次冲击后的岩石破碎面积基本一致,但在第8 次冲击后30 J 的破碎面积不再增加,25 J 的仍继续保持面积扩大的趋势;冲击功为40 J 与35 J时,第7 次冲击结束后,岩石的破碎面积不再增大,且10 次冲击后35 J 破碎面积略低于40 J。

图11 实验、模拟破碎面积对比曲线Fig.11 Comparison curves of experimental and simulated crushing areas
在实验与模拟过程中,冲击功为20 J 时,球齿冲击岩石后产生的应力最大为86.96 MPa,此时应力波传递范围与主要应力都较小,导致岩石破碎面积小,为20.2107 mm2。随着冲击功的的增大,应力最大值变为95.66 MPa。在25 J 时,球齿与岩石接触点下方应力变大,且接触点左侧应力明显高于右侧,导致岩石破碎面积发生第1 次突变为40.1968 mm2。冲击功为30 J 时,岩石破碎面积与25 J 时一致。当冲击功为35 J 时,接触点下方的应力达到岩石的抗拉强度,且接触点右侧应力相比于冲击功30 J 时增大,导致岩石破碎面积发生第二次突变为52.8858 mm2。冲击功为40 J 时,岩石破碎面积与35 J 一致,且不再增大。
图12 为实验与模拟球齿在不同冲击功情况下破碎比功的对比曲线,可知实验中随着冲击次数的增加,当冲击10 次时,破碎比功从大到小排列依次是:35、40、25、30、20 J。在模拟中破碎比功从大到小排列依次是:40、35、30、25、20 J。综合考虑实验与模拟情况,认为在实验过程中由于在花岗岩中存在不同的岩石杂质且分布不均,因此导致岩石的不同位置具有的硬度存在差别,且在实验中岩石在受到冲击作用后破碎岩石,产生的破碎坑周围的岩石容易脱落,使得破碎面积增大。所以在实验与模拟中球齿采用相同冲击功冲击情况下,所产生的破碎比功存在差异。

图12 实验、模拟破碎比功对比曲线Fig.12 Experimental and simulated rock breaking specific energy comparison curves
2.4 实验与模拟结果讨论
通过实验与模拟分析可知,冲击功为40 J 时岩石的破碎面积最大但破碎比功相比于其它冲击功来说较大;冲击功为35 J 时破碎面积与破碎比功较40 J 时都小;冲击功为30 J 时破碎面积近似于35 J,但破碎比功却较35 J 小;冲击功为25 J 时破碎面积小于30 J,破碎比功大于30 J;冲击功为20 J 时,破碎面积为最小,但破碎比功小于30 J。结合考虑现场施工等情况,可知当选用冲击功40、35 J 时,潜孔锤能量损耗较大且钻头寿命较短;当选用冲击功20、25 J为球齿冲击功破碎相同面积时,所需的时间较长且容易导致破碎不完全等问题;当冲击功30 J 为球齿冲击功时,破碎面积较大且破碎比功也较小。因此选用30 J 作为球齿最优冲击功,能有效降能量损耗、减少现场施工时间和增加钻头使用寿命。
3 结论
本文采用ABAQUS 软件建立在不同冲击功条件下球齿冲击碎岩的模型,对岩石破碎进行数值模拟研究,得到破碎面积与破碎比功在不同冲击功下的变化规律。分析冲击过程中岩石的破碎面积、裂纹与应力波情况,并生成曲线图进行对比分析,得出球齿最优冲击功为30 J,结论如下:
(1)随着冲击功的增大,岩石破碎深度与面积也随之增大,但由于破碎深度增加,当钻头回转时,球齿克服岩石抗剪强度所需要的能量较多,球齿磨损增加,且破碎比功不会随着冲击功增大而减小。同时考虑到钻头使用寿命以及降低能耗和减少现场施工时间等因素,选用冲击功为30 J 作为球齿最优冲击功。
(2)对模拟中岩石von-mises 应力变化进行分析。当冲击功为30 J 时,岩石在破碎过程中von-mises 应力值主要集中在 8.33~66.67 MPa 之间,部分密实核区域应力值会达到86.96 MPa。岩石受到冲击作用,产生破碎,碎岩机理根据模拟可分为3 个阶段:弹性变形、压裂、体积破碎。
(3)对球齿冲击过程中的应力波进行分析,可知应力波以球齿与岩石最初始接触点为中心呈半球形扩散,遇到岩石边界时反弹,最终消失。岩石裂纹首先产生于球齿与岩石表面的接触点,使得岩石表面更容易发生破碎。同时中间裂纹扩展速度最快,而径向裂纹扩展速度快于侧向裂纹。
