HTPB 推进剂/衬层界面Ⅰ型破坏温度相关特性

丁 伍，许进升，周长省，王庭钰，侯宇菲

（南京理工大学 机械工程学院，江苏 南京 210094）

1 引言

固体火箭发动机结构简单，应用成熟，可靠性高，是小型火箭弹、多数军用导弹的主流动力源。针对应用广泛的贴壁浇铸式固体火箭发动机，其燃烧室壳体通过均匀喷涂的胶黏剂与绝热层黏接在一起，在绝热层上涂着薄薄的一层衬层，端羟基聚丁二烯（HTPB）推进剂浇铸在空腔内部并固化成型，待其固化后，燃烧室内会形成一个由推进剂、衬层和推进剂基体即丁羟胶组成的界面系统［1］。由于固体推进剂药柱的热膨胀系数与壳体和衬层都有着较大的差异，固体火箭发动机固化降温时会导致各部件体积收缩，产生初始应力，并在之后的温度循环中不断地积累损伤，最终影响固体火箭发动机的结构完整性。

目前，对于固体火箭发动机的推进剂/衬层黏接界面的温度特性的研究主要有实验分析和数值仿真两个方面。实验主要集中在对黏接界面的强度测定［2-4］、裂纹扩展分析［5-6］、组分迁移［7］和界面破坏机理［8］等方面。数值仿真常用的方法主要有内聚力模型和拓展有限元，且由于内聚力模型在解决界面问题时不需考虑裂纹尖端的应力奇异点，得到了广泛的应用［9-12］。尽管一些常用的内聚力模型能够用来分析推进剂/衬层黏接界面的破坏，但有时分析的效果并不太理想。Needleman［13］在研究内聚力模型时认为，内聚法则中的参数比内聚力曲线的形式更重要。但Chandra［14］等发现选择合适的内聚力曲线更能准确地描述实验结果。Volokh［15］更是证实了不同曲线形式能够显著影响数值仿真结果。Högberg 等［16］指出针对不同模式的界面破坏，应该使用更加灵活的内聚力模型来模拟黏接层的本构行为。国内外的一些学者［17-20］针对不同的界面破坏提出了更多形式的内聚力模型，为研究固体推进剂/衬层黏接界面的破坏提供了很好的借鉴。

为了能够更加真实地研究固体发动机黏接界面的实际破坏情况，本研究从试验和数值仿真两方面研究固体火箭发动机的HTPB 推进剂/衬层界面Ⅰ型破坏和变温力学性能，并在双线性内聚力模型的基础上构建了一种损伤演化为多项式函数的内聚力模型，为固体火箭发动机结构完整性分析提供一定的理论基础。

2 实验与分析

2.1 实验方法

为了测试HTPB/衬层黏接界面的Ⅰ型破坏温度相关力学性能，根据标准QJ 916-1985［21］，设计了试件和夹具。两个平行钢件上分别浇筑推进剂、涂敷衬层和黏接绝热层，即构成了试件，并在其中一个钢件的衬层两端，分别人为造成绝热层与推进剂之间有20 mm×20 mm的破坏面，如图1 所示。试件通过夹具与试验机配合良好，垂直于试件黏接面的方向上施加拉力，在不同的温度下测量试件破坏时的应力。根据固体火箭实际贮存温度，设计了6 个实验温度点：-40，-20，0，20，40，60 ℃。采用高低温试验箱控制黏接试件所处的温度环境，室内相对湿度保持在42%，实验前需将试件放在高低温试验箱中在指定温度下保温2 h，保证试验时试件所有部位都处于相同的温度条件下，然后以20 mm·min-1的恒定速率拉伸试件，每个相同的温度条件下重复5 次实验并记录载荷位移曲线。拉伸过程中采用高清摄像机拍摄拉伸过程中试件的裂纹扩展情况，在试件的侧面上黏接带有刻度的光栅，每小格尺寸为1 mm，刻度与预制裂纹对齐以定量表示裂纹尖端的破坏过程。

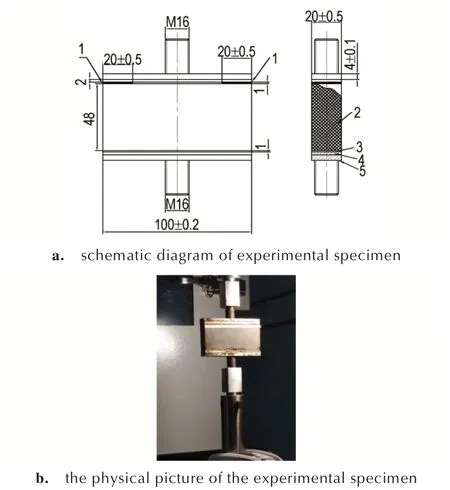
图1 单轴拉伸实验试件1—预制裂纹，2—HTPB 推进剂，3—衬层，4—绝热层，5—钢件Fig.1 The experimental specimen1—prefabricated cracks，2—HTPB propellant，3—liner，4—insulation，5—steel parts

2.2 实验结果

2.2.1 破坏过程

以-20 ℃下的实验试件作为研究对象。该试件在10.2，12.5，15.5，16.76 s 时刻的黏接界面破坏过程如图2 所示，对实验数据处理得到相应的载荷-位移曲线如图3 所示。图2 中的时刻分别对应于曲线上的A、B、C、D4 点，展示了从损伤开始、裂纹产生、损伤拓展和完全失效的过程。由图3 可见，试件的破坏过程可分为三段，第一阶段OA为线弹性阶段，黏接界面没有明显的变化，到A点时可以观察到黏接界面产生微小纤维化损伤，AB段拉伸载荷的变化不再呈线性增长。当到B点时，拉伸载荷达到最大值，预制裂纹尖端钝化，黏接界面开始破坏。从峰值点B以后黏接界面裂纹先稳定扩展后迅速扩展，直至D点完全失效。

图2 实验试件的黏接界面破坏过程Fig.2 Failure process of bonding interface of experimental specimens

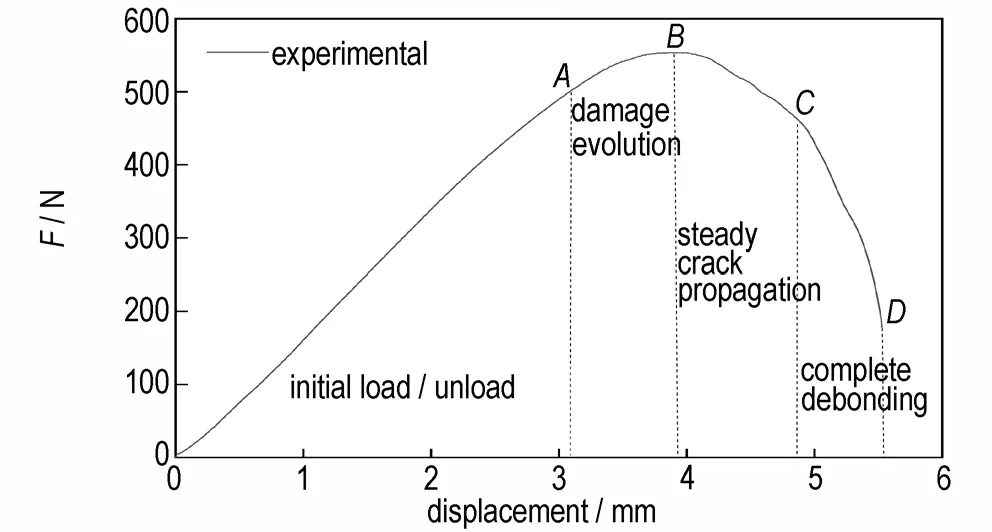
图3 载荷-位移曲线Fig.3 Load-displacement curve

黏接界面的破坏形式有3 种，分别是内聚破坏、界面破坏和混合破坏。内聚破坏发生在胶黏剂或者被黏接物上，界面破坏发生在黏接界面处，而混合破坏则同时含有内聚破坏和界面破坏［22］。在-20 ℃下的实验结果如图4 所示。由图4 可知，黏接界面的破坏为发生在HTPB 推进剂上的内聚破坏，说明黏接强度和胶黏剂强度高于HTPB 推进剂本身的强度，表明胶黏剂本身的强度及黏接效果可充分满足使用要求。

图4 黏接界面破坏类型Fig.4 Types of bond interface failure

2.2.2 特征参数

通过实验获取了42%的湿度下，HTPB/衬层黏接界面Ⅰ型破坏在不同温度条件下的平均载荷-位移曲线，如图5 所示。由图5 可知，当温度降低时黏接界面的强度和断裂能均增大，尤其在低温233.15 K 时黏接界面的断裂能和强度明显上升。从图5 可以看出，峰值点载荷所对应的位移即特征位移也有明显的温度相关性，当在低温时，随着温度的降低，特征位移减小；在高温时，随着温度的增加，特征位移也在减小。这说明在低温时黏接界面韧性降低发生了脆断，在峰值点后载荷急速下降也能证明这一点。在高温时，裂纹尖端的塑性区会承受较大的塑性变形，界面内应力的多轴性引起孔洞的形成与合并，导致界面损伤提前发生。

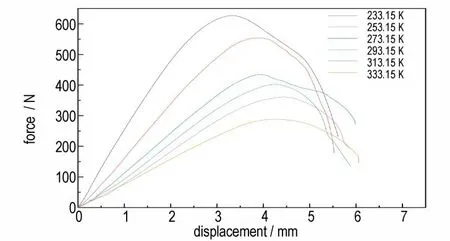
图5 不同温度下载荷-位移曲线Fig.5 Force-displacement curves at various temperatures

黏接界面力-位移曲线的峰值点对应于最大载荷Fmax，与位移所围成的面积即为断裂能G。内聚强度为σ=Fmax∕S，Ⅰ型破坏的单位面积断裂能为Gn=G∕S，根据实验试件黏接处面积S=1200 mm2，即可获取HTPB/衬层黏接界面Ⅰ型破坏在不同温度下的内聚强度和单位面积断裂能，如表1 所示。

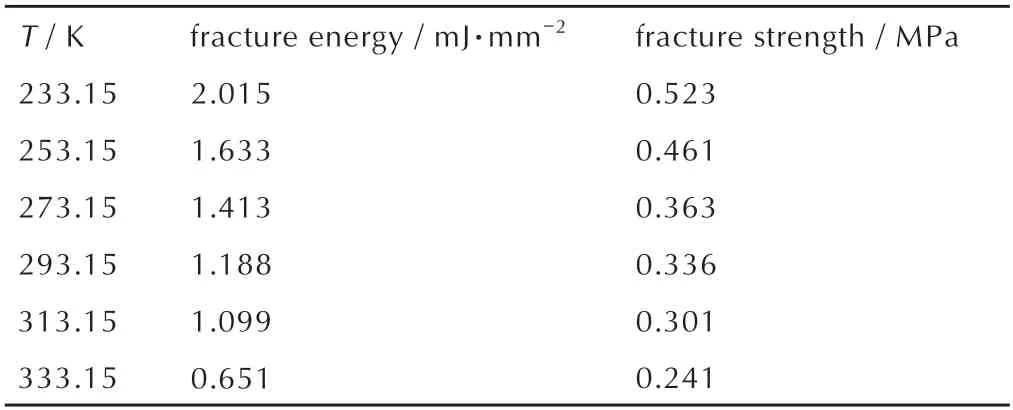
表1 各温度下试件黏接界面参数Table 1 Bonding interface parameters of specimens at different temperatures

为了能够更好地研究温度对黏接界面的影响，在一定范围内预测黏接界面的力学性能，根据不同温度下的平均断裂能、内聚强度和特征位移的变化规律，拟合了相应的曲线，如图6 所示。

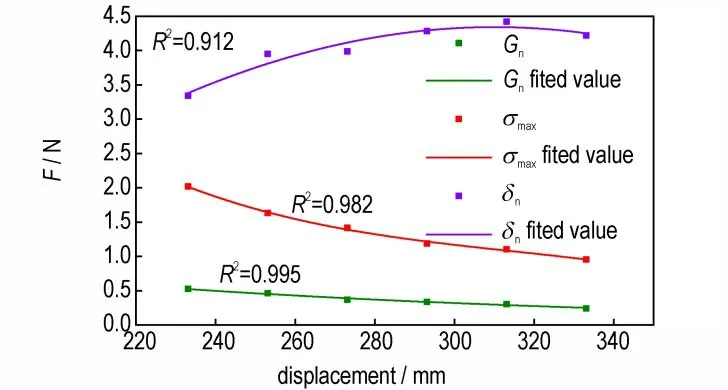
图6 Gn、σmax 和δn 的拟合结果Fig.6 Fitting results of Gn，σmax and δn

采用式（1）拟合断裂能与温度的关系，根据实验的拟合结果θm=0.735 mJ·mm-2，θ=57.727 K。

对于内聚强度，采用式（2）拟合了内聚强度随温度变化的规律，其中参考温度T0=293.15 K，参考点内聚强度σ0max=0.3356 MPa，拟合曲线的k=2.168。

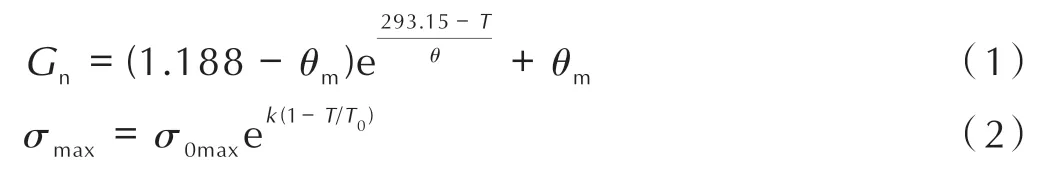
特征位移采用三次多项式来拟合，拟合结果如式（3）所示：

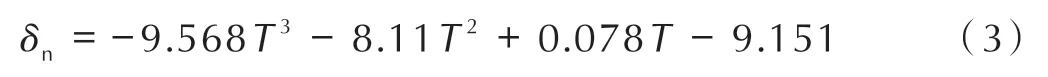
在Origin中拟合公式的决定系数R2表示拟合相关度的大小，图中的R2在0.9 以上，说明拟合的结果能够很好地述特征参数随温度变化的规律。

3 内聚力模型

3.1 基于损伤的双线性内聚力模型

双线性内聚力模型是发展最为成熟的内聚力模型，常用来模拟复合材料的分层和黏接界面的破坏。通过考虑黏接界面的累计损伤定义了损伤变量，双线性模型的法向和切向内聚法则可以表示如（4）式［19］：

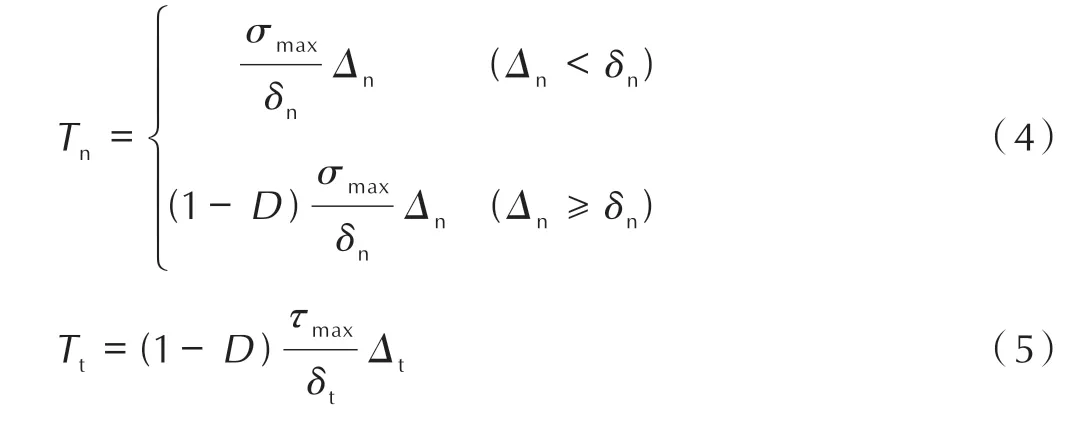
其中，下标n 和t 用来表示法向和切向行为，T表示牵引力，N；σmax和τmax分别表示法向和切向内聚强度，MPa；δ和Δ分别是特征长度和分离位移，mm。D是损伤因子，表示材料的整体累积损伤，当损伤D=0 时界面没有损伤，而D=1 时界面完全破坏。其表达式如下［23］：

图7 展示了双线内聚力法则的纯Ⅰ型和纯Ⅱ型的张力位移关系。

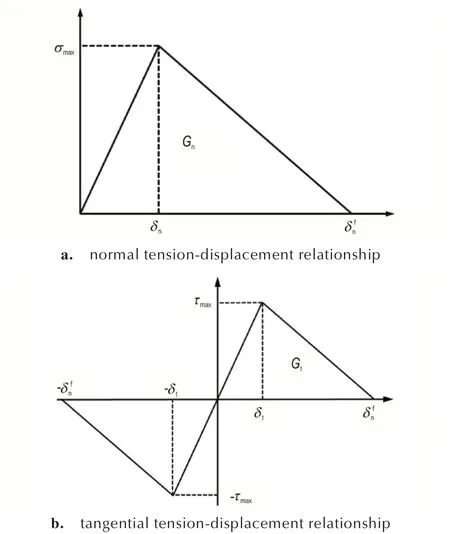
图7 双线性内聚力模型Fig.7 Bilinear cohesive law model

3.2 构建线性-多项式内聚力模型

根据2.2.1 节的分析，黏接界面的损伤在峰值点载荷之前就发生了，在峰值点之后损伤迅速扩展。基于此重新定义了损伤变量来表示损伤演化形式，损伤发生之前黏接界面与双线性内聚力模型的上升段相同，当达到损伤点是开始按照自定义损伤演化函数进行损伤演化，其损伤变量和内聚力法则分别如式（9）和式（10）所示，法向时m 为n，切向时m 为t。如图8 所示，线性段和损伤段的断裂能分别为GmⅠ和GmⅡ，损伤起始点为δm1及其对应的应力σ1，具体参数值由试验确定。当损伤起始点确定后，能够决定自定义内聚力模型的特征参数主要有特征位移δm、内聚强度σmax、失效位移和断裂能Gm，只需要确定其中一个参数就能确定损伤参数a、b和c，进而得出损伤变量D′，确定损伤演化形式。

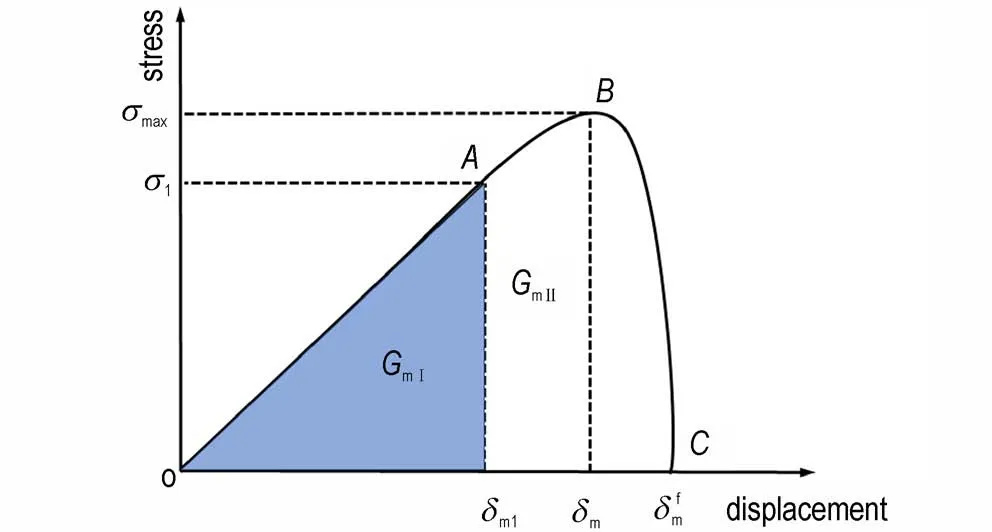
图8 线性-多项式内聚力模型Fig.8 Linear-polynomial cohesive law model

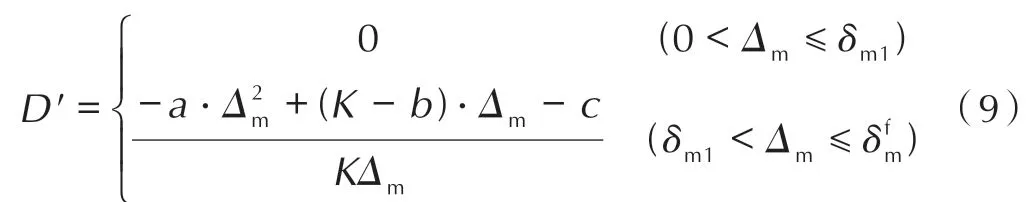
其中K=σ1∕δm1，a、b和c为损伤参数。

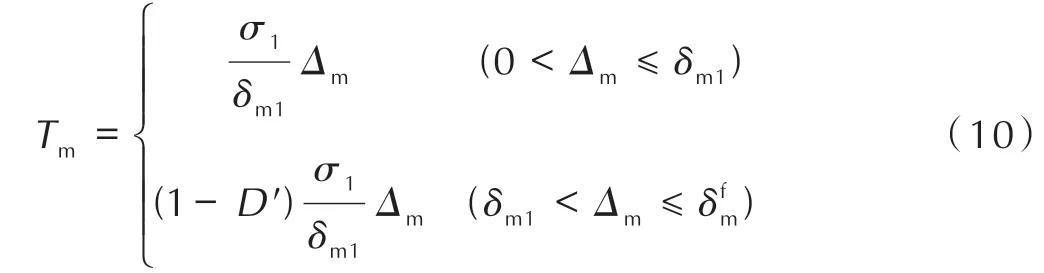
将损伤变量表示为Δm的多项式函数，其形式为：

黏接界面的断裂能满足关系式［23］：

其中线性段的内聚能和损伤段的内聚能分别表示为：

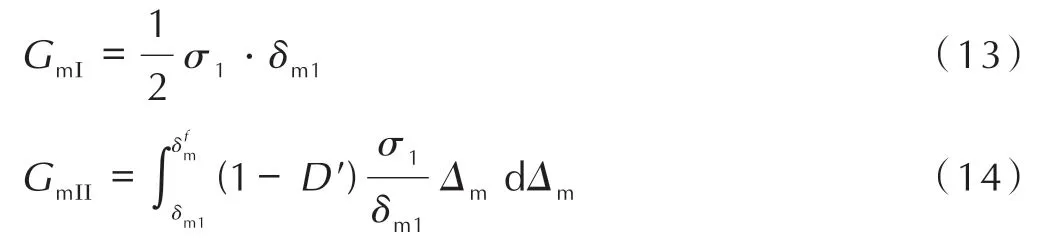
若保证在损伤起始点线性段和损伤段能够连续，首先需满足式（15）和式（16）：

在已经满足式（15）和式（16）后，若以特征位移和内聚强度(δm，σmax)作为已知特征参数来确定损伤变量时，需要增加满足条件式（17）；若以临界位移作为已知特征参数来确定损伤变量时需满足式（18）；若以断裂能Gm作为已知特征参数来确定损伤变量时需满足式（19）：

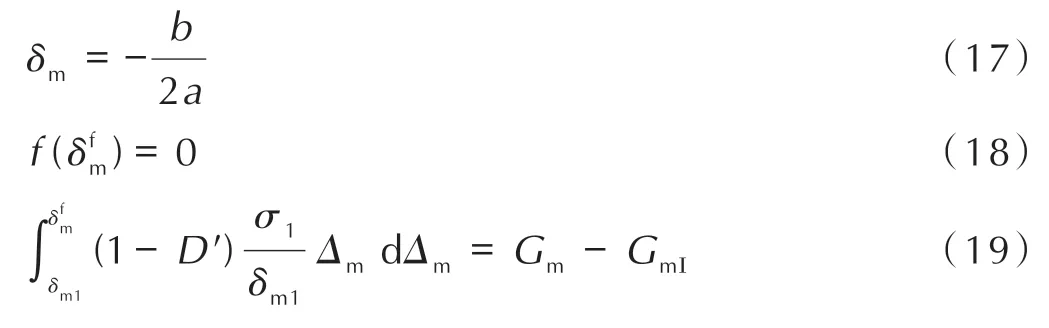
将单一模式损伤演化规律扩展到混合模式损伤时，主要在于获取混合加载下的损伤起始点位移和等效临界位移。初始损伤对应于材料开始退化，当应力满足于定义的初始临界损伤准则，则此时退化开始。常用的损伤起始准则有二次应力准则，损伤演化准则为幂律准则。

σ和τ分别为法向应力和切向应力，σ1和τ1分别为法向强度和切向强度，由公式σ=KΔn，τ=KΔt，将σ1和τ1代入平方应力准则得到混合应力下损伤起始点位移δe1：

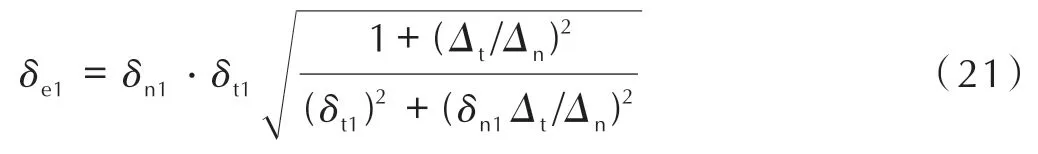
混合界面下的损伤演化可以用幂律准则表示［12］：

式中，Gn为法向断裂能，Gs和Gb分别为两个切向断裂能由公式（12）计算得出，将切向断裂能耦合得到Gt=Gs+Gb，Gnc和Gtc分别为法向和切向断裂韧度，将式（12）、式（13）和式（14）带入幂律准则可获取等效临界位移即，混合应力状态下的损伤变量为，其中ae、be和ce为混合应力状态下的损伤参数。

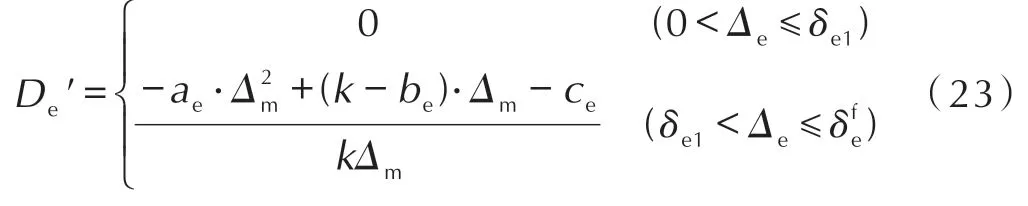
当Δe≤δe1时，界面没有损伤，此时界面载荷与位移呈线性关系，界面载荷为Tm=KΔm；当δe1≤Δe≤时界面开始损伤演化，界面载荷为Tm=(1-)KΔm；当Δe≥时界面完全失效。

4 数值仿真

为了更真实地模拟实验，用商业有限元软件ABAQUS 对实验试件进行建模，建立了三维试件模型并分别对模型设置了材料属性、网格单元划分和边界条件，其中界面材料本构采用用户定义材料子程序（UMAT）来定义。所建立的模型尺寸与试件尺寸完全一致。衬层、绝热层和钢件的材料参数见表2，实验中所采用的推进剂为HTPB 推进剂，它是一种颗粒增强型的黏弹性材料，泊松比为0.499。常用Prony 级数来表达其黏弹性本构关系，Prony 级数的形式如式（24）所示［24］。时温等效模型由WLF 方程表示如式（25）所示［25］；并在衬层与推进剂之间设置0.2 mm 的界面层，采用8 节点COH3D8 内聚单元，对三维实验模型划分网格如图9a 所示。壳体、推进剂、绝热层采用8 节点的C3D8T 六面体单元。根据实验状况设置边界条件，壳体和绝热层、绝热层与衬层、衬层与界面层和界面层与推进剂均采用绑定约束。下层壳体完全固定，上层壳体施加位移载荷。在ABAQUS 中把构建的自定义内聚力模型编入UMAT 用户定义材料子程序中，对拉伸实验进行仿真。

表2 衬层、绝热层和钢件的材料参数［26］Table 2 Mechanical parameters of lining，insulation and steel parts

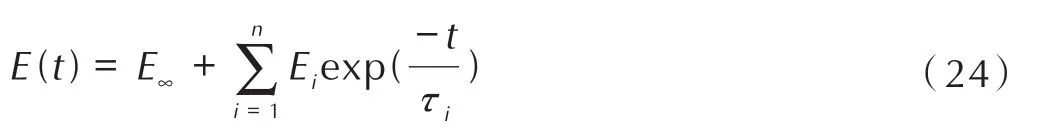
式中，Ei，τi，E∞通过实验获取，根据以往的研究［24］，在20 ℃下Prony 级数的拟合结果如表3 所示。

表3 HTPB 推进剂松弛参数Table 3 Relaxation parameters of HTPB propellant

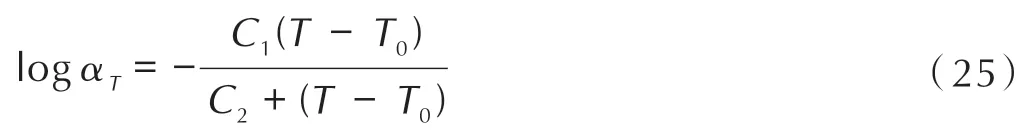
式中，C1=2.05852，C2=172.10762，T0=293 K。

在建立模型后，分别以特征位移δm，失效位移和断裂能Gm作为已知特征参数来确定损伤变量值，进而预测损伤起始点之后的损伤演化形式。由图9b可知，在20 ℃时当特征位移δm作为已知参数时，数值预测的线性段和损伤段都能较好的与实验测得的载荷-位移曲线重合。而当采用失效位移作为已知特征参数来预测时，线性段的结果能够与实验结果很好的贴合，但峰值点与实验曲线还存在一定的误差。当采用断裂能Gm来预测时，损伤段峰值点和演化过程均存在一定偏差，各损伤参数如表4 所示。因此，为了准确预测黏接界面的损伤演化过程，选择以特征位移δm作为已知特征参数，预测不同温度下的黏接界面的损伤情况，损伤参数如表5 所示。

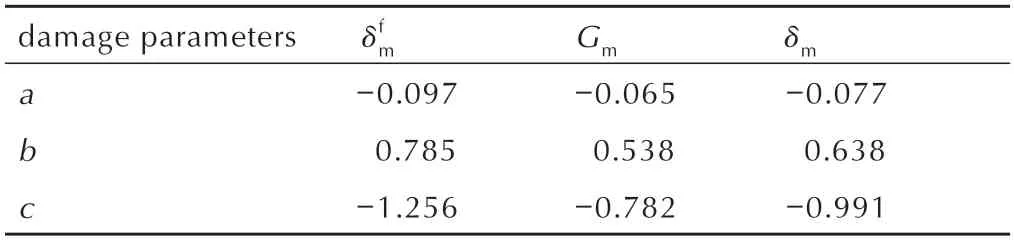
表4 分别以δf、Gm 和δm 为特征参数时的损伤参数Table 4 The damage parameters with δf，Gm and δm as characteristic parameters respectively

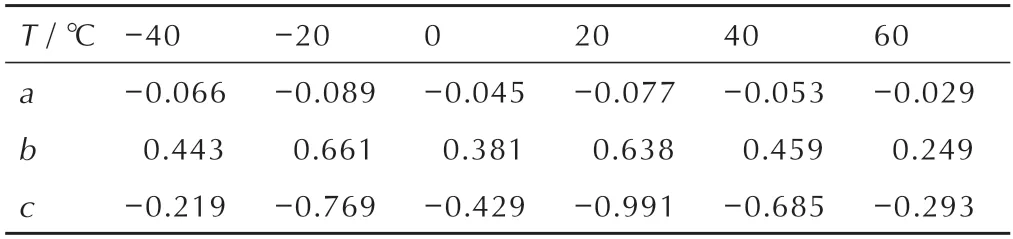
表5 不同温度下的损伤参数Table 5 Damage parameters at different temperatures

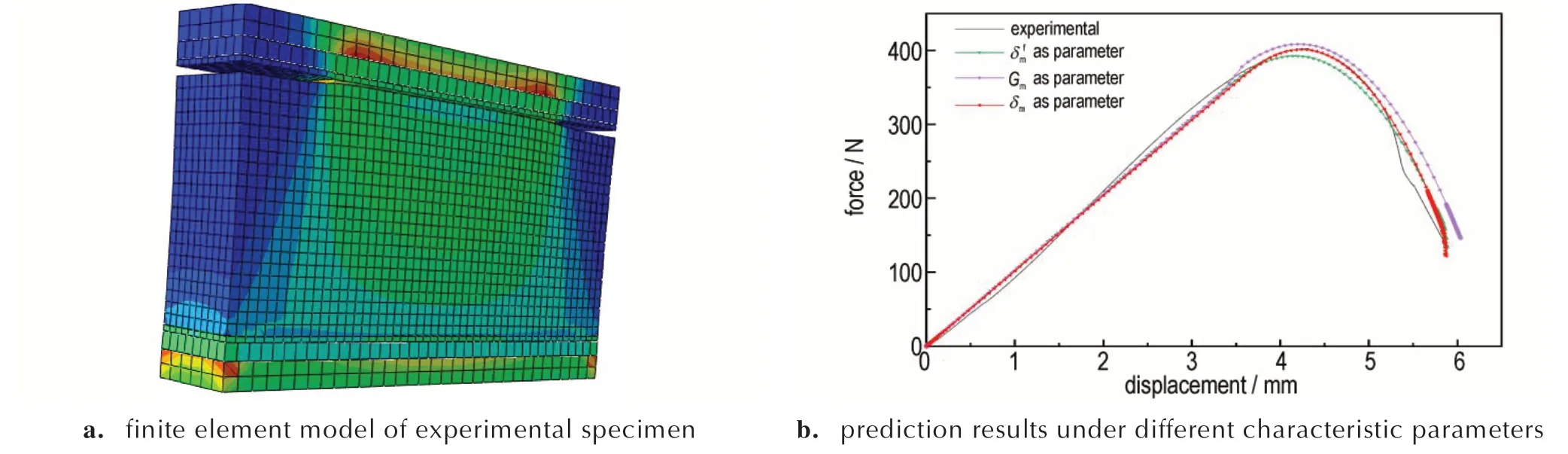
图9 拉伸试件的数值模型和不同特征参数下的分析结果Fig.9 Numerical model of tensile specimen and analysis results under different characteristic parameters

根据图10 中的仿真预测的结果可知，在温度从-40 ℃上升到60 ℃的过程中，双线性内聚力模型和自定义内聚力模型所预测的内聚强度都减小，特征位移随温度先升高后减小。双线性内聚力模型在预测各温度下的载荷-位移曲线时，线性段与实验获得的曲线能够较好的符合但在应力损伤段误差较大；而自定义内聚力模型不仅能够准确地预测各温度下线性段受力状况，也能够准确地描述损伤段的载荷-位移曲线。这表明自定义的内聚力模型比双线性内聚力模型更适用于固体火箭发动机界面Ⅰ型破坏的在不同温度下的力学特性。

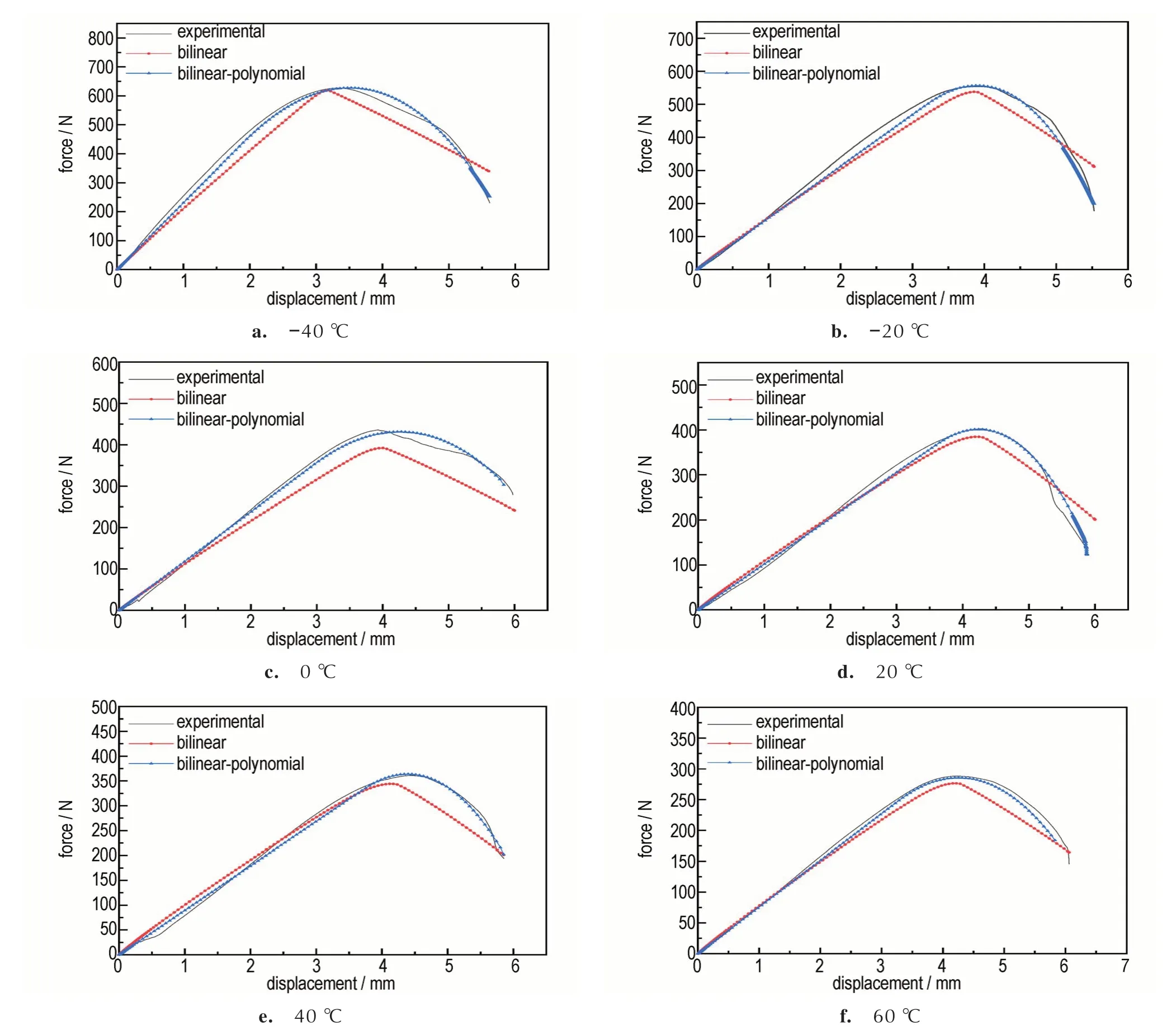
图10 不同温度下拉伸试件的仿真结果Fig.10 Simulation results at different temperatures

5 结论

（1）从实验中发现随着温度的变化黏接界面的位移-载荷曲线有着明显的规律。当温度降低时黏接界面的强度和断裂能均增大，尤其在低温-40 ℃时黏接界面的断裂能和强度明显上升，分别达到了2.015 mJ·mm-2和0.523 MPa。

（2）峰值点载荷所对应的位移即特征位移也有明显的温度相关性，当在低温时，随着温度的降低，特征位移减小；在高温时，随着温度的增加，特征位移也在减小。这说明在低温时黏接界面韧性降低发生了脆断。在高温时，裂纹尖端的塑性区会承受较大的塑性变形，界面内应力的多轴性引起孔洞的形成与合并，导致界面损伤提前发生。为了能够更好地研究温度对黏接界面的影响，在一定范围内预测黏接界面的力学性能，根据不同温度下的平均断裂能、内聚强度和特征位移的变化规律，拟合了相应的曲线公式。

（3）在双线性内聚力模型的基础上构建了一种损伤演化形式——多项式的内聚力模型，讨论了不同特征参数在预测不同温度下的黏接界面力学特性的准确性，并以特征位移为特征参数预测了不同温度下的黏接界面载荷-位移曲线，数值预测结果与实验结果一致；说明该模型能够比双线性内聚力模型更加真实准确地反映Ⅰ型破坏温度相关特性。