基于改进粒子群算法的汽油辛烷值损失优化
2022-02-15谢忻南饶伟浩薛美盛
谢忻南 饶伟浩 薛美盛
(中国科学技术大学信息科学技术学院)
汽油是小型车辆的主要燃料,汽车燃烧产生的尾气排放后对大气环境有着较大的影响。 如何充分利用现有的油品资源,以更低的成本生产出更多的高质量汽油,是油品调和过程中需要解决的问题[1]。 汽油清洁化的重点在于降低汽油中硫和烯烃的含量,同时尽量保持其辛烷值。 辛烷值是反映汽油燃烧性能最重要的指标,现有的技术在对催化裂化汽油进行脱硫和降烯烃的过程中,普遍降低了汽油的辛烷值,这样也就造成了巨大的经济损失。
化工过程建模一般通过数据关联或机理建模的方法实现,但由于炼油工艺过程复杂且设备多样,过程的变量之间具有高度非线性关系和强耦合关系,而且传统数据关联模型中变量相对较少,机理建模对原料的分析要求较高,对过程优化的响应不及时,因此采用机理模型效果并不理想,辛烷值损失仍有较大的优化空间。
近年来许多学者也对此领域展开了相关研究。 在汽油的生产过程中存在大量与辛烷值相关的变量,在建立辛烷值预测模型之前,需要对这些变量进行处理,筛选出与辛烷值具有强相关属性的变量,现有的研究[2~4]在寻找建模的主要变量时,大多基于工程经验,选择的变量差异较大。 杜明洋等使用随机森林法选择变量[5],虽然不再依赖工程经验,但未考虑变量之间的关联性与耦合性。 陈曦等采用PCA方法选择变量[6],同样未考虑变量之间的耦合性。
辛烷值预测模型主要分为机理模型与基于人工神经网络的模型。 机理模型以早期的Nelson模型[7]、Stewart模型[8]与Ethyl-R-70模型[9]为代表,如前所述机理模型存在预测辛烷值精确度不高的问题。 随着人工神经网络技术的发展,基于人工神经网络建立预测调和汽油辛烷值模型的研究逐渐成为热点。 2000年,Chibaro E等提出一种基于BP神经网络的汽油辛烷值预测模型[2],模型选择21个变量作为输入,最终输出包括预测辛烷值在内的4个变量。 这种模型在汽油属性发生变化时,需要重新采集数据进行训练,在实际应用中较为困难。2004年,Murty B S N和Rao R N提出了另外一种基于神经网络的辛烷值预测模型[3],模型选择14个变量作为输入,最终输出预测辛烷值。 这种模型同样存在适应性不强的问题。 2009年,Paranghooshi E等提出一种将6种变量作为输入变量的人工神经网络模型[4],该模型的预测精度高于传统的回归模型, 该方法的适应性不强,当汽油属性发生变化时,往往需要重新采集数据训练网络。 文献[10~12]同样将BP神经网络用于辛烷值的预测问题上, 并取得了良好的效果。2020年,李炜等提出了一种基于SHPSO-GA-BP的汽油辛烷值组分预测方法[13],将粒子群算法、遗传算法与BP神经网络相结合,进一步提高了汽油辛烷值预测的精度。 2021年,朱悦晨和李江涛将支持向量机引入辛烷值预测模型的研究当中[14]。谢鑫等将二阶段异质随机森林引入到汽油辛烷值预测的研究当中[15]。 以仪器分析为基础获取辛烷值也是一类非常重要的方法[16~18],但是这类方法依赖分析仪器,不适用于大部分场合。
1 问题分析
在实际生产过程中,与辛烷值相关的变量有数百个。 笔者所采用的辛烷值数据包括7个原料性质,2个待生吸附剂性质,2个再生吸附剂性质,2个产品性质以及另外354个操作变量, 共计367个变量。 在建立辛烷值预测模型之前,通常需要在这些变量中选择部分与辛烷值相关性较大的变量进行处理。 同时由于化工流程的变量之间一般都具有很强的耦合性和关联性,在依据相关性进行变量选择的同时,还需要根据变量之间的耦合性对选择出来的变量进行调整。 笔者利用随机森林法(Random Forest,RF)[19]分析各个工业变量与辛烷值的相关性, 利用最大信息系数(Maximal Information Coefficient,MIC)[20]与皮尔森相关系数(Pearson Correlation Coefficient,PCC)[21]分析各个工艺变量之间的耦合关系,筛选出重要的变量。
在此基础上,建立基于BP神经网络与模糊神经网络的汽油辛烷值预测模型,以提高汽油辛烷值预测模型的精确度与适应性。BP神经网络的优势是泛化能力强, 自组织性和自学习性都较好。但是BP神经网络属于局部搜索的优化算法,在解决复杂的优化问题时,极易陷入局部极值,导致网络训练不成功。并且BP神经网络对初始的网络权重非常敏感,不同的权重初始化网络,每次的收敛结果都极容易收敛到不同的局部极值。 模糊神经网络能够对BP神经网络的这一特点进行进一步优化,它可以充分利用专家经验,使得模型训练的结果更加可靠真实。
此外,笔者提出了一种改进粒子群算法对辛烷值损失进行优化。 改进粒子群算法通过改进搜索步长和边界条件,可以满足实际生产中,工业装置为了平稳生产,主要操作变量只能逐步调整到位, 即每次允许调整幅度值为确定值的要求。同时,改进粒子群算法与基础粒子群算法相比在达到相同优化效果时, 所需的粒子数量更少,因此提高了优化速度。 笔者采用的辛烷值均为研究法辛烷值ROH。
2 变量选择
笔者利用随机森林法分析各个工业变量与辛烷值的相关性, 利用MIC与PCC分析各个工艺变量之间的耦合性。
笔者所采用的变量选择方法如图1所示,选取变量的原则是:

图1 变量选择流程
a. 变量的排名前后依据的是与产品中辛烷值的含量相关性的强弱,此时的相关性根据随机森林法计算得到;
b. 在根据随机森林法得到与辛烷值含量相关性排名靠前的变量后, 利用MIC和PCC方法检查变量之间的耦合性,进一步进行变量的筛选。
使用如下变量选择算法对变量进行排名:



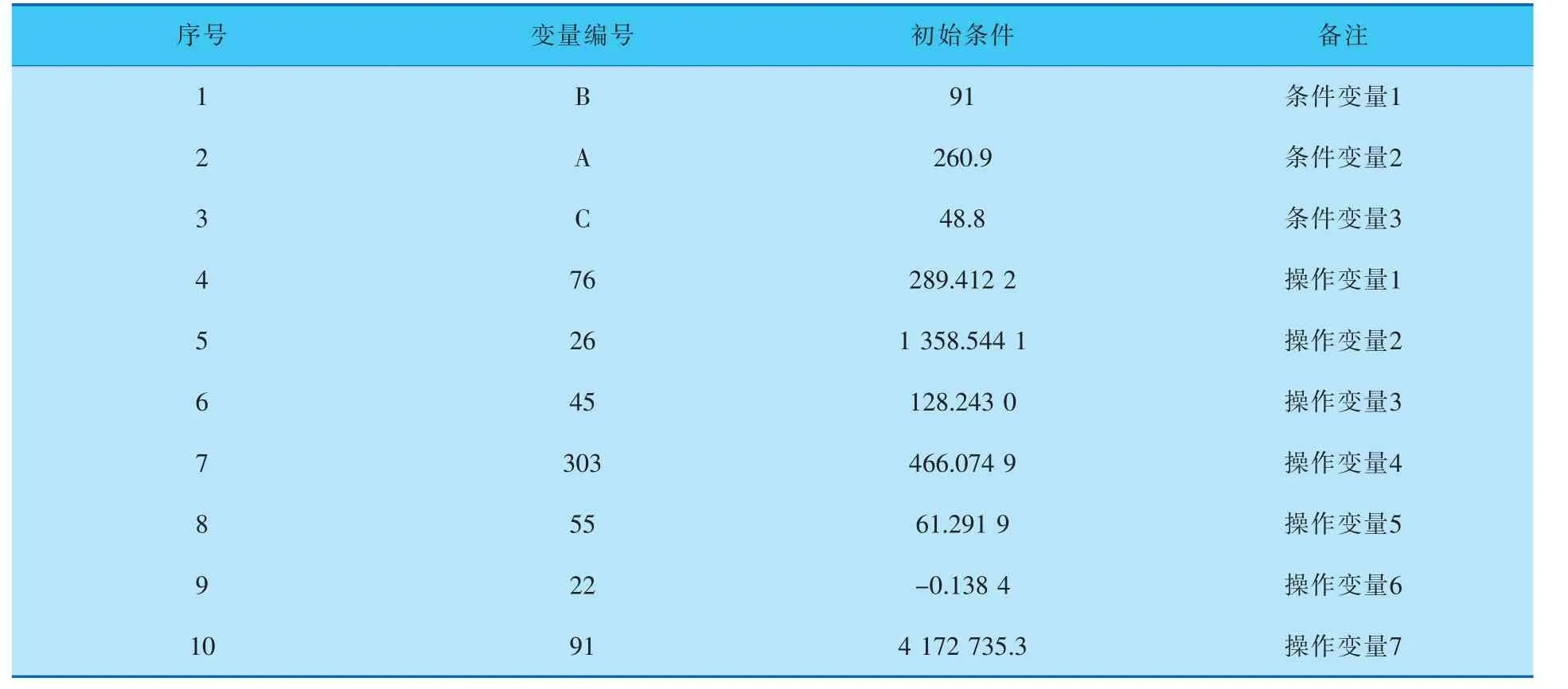
选择变量排名靠前的特征进行辛烷值预测模型的建模工作,得到的10个工艺变量见表1。

表1 选择的建模变量
3 建立预测模型
3.1 辛烷值预测模型
笔者将BP神经网络与模糊神经网络进行结合,预测模型的结构如图2所示。

图2 辛烷值预测模型
预测模型的输入为第2节中选择的10个变量, 经过BP神经网络和模糊神经网络的处理后,输出产品的辛烷值。
笔者采用的BP神经网络和模糊神经网络的结构参数见表2。

表2 神经网络结构设置
笔者将10个变量的325组数据分为训练集和测试集,其中90%的数据放入训练集,10%的数据放入测试集。 样本输入到两个神经网络进行训练,可以分别获得神经网络的权重。 在预测数据时,结合两个神经网络输出的预测产品中的辛烷值,以获得预测结果。
3.2 辛烷值预测结果
辛烷值预测结果如图3所示, 可以看出笔者所提的预测模型对产品辛烷值的预测结果与真实值接近,这说明笔者所提的预测模型对产品辛烷值的预测效果好,有效性较高。

图3 产品中辛烷值的预测结果
图4是辛烷值损失预测结果和误差。 其中,辛烷值损失的预测结果是原料中的辛烷值与预测的产品辛烷值的差值;辛烷值损失误差即辛烷值损失的真实值与预测值的差值。 从图4a中能够看到,该预测模型的输出接近真实输出,两条曲线的变化趋势基本相同;由图4b可知,辛烷值损失误差最大在0.75左右, 表明笔者所提预测模型的准确性较高。
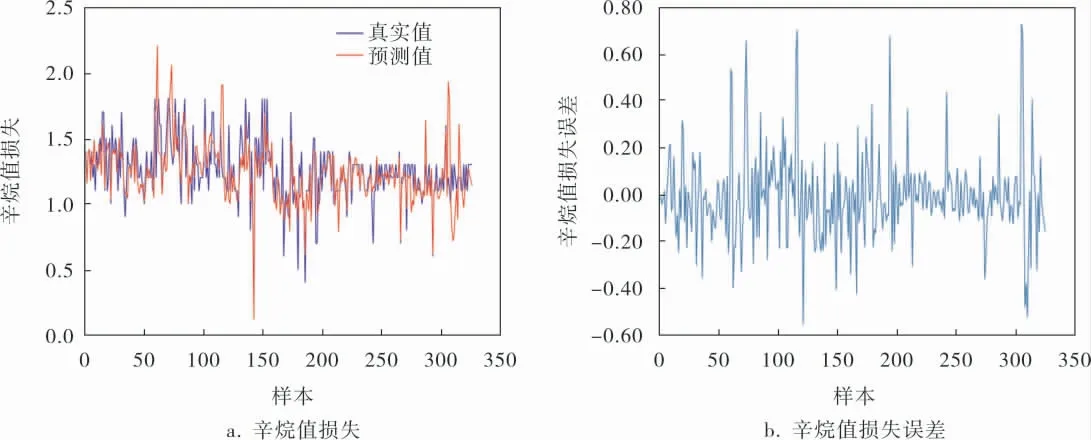
图4 辛烷值损失预测结果和误差
4 改进粒子群算法
4.1 基本粒子群算法
假设在D维的目标搜索空间中,有N个粒子组成一个族群, 其中第i个粒子表示为一个D维向量,记为Xi=(xi1,xi2,…,xiD),i=1,2,…,N,第i个粒子的移动速度也是一个D维向量,记为Vi=(vi1,vi2,…,viD),i=1,2,…,N,第i个粒子目前搜索到的最优位置称为个体极值,记为pbest=(pi1,pi2,…,piD),i=1,2,…,N,整个粒子群目前搜索到的最优解为全局极值,记为gbest=(g1,g2,…,gD)。
基本粒子群算法[22]流程如下:
a. 初始化粒子群,包括群体规模N、每个粒子的位置Xi和速度Vi;
b. 计算每个粒子的适应度值fit[i];
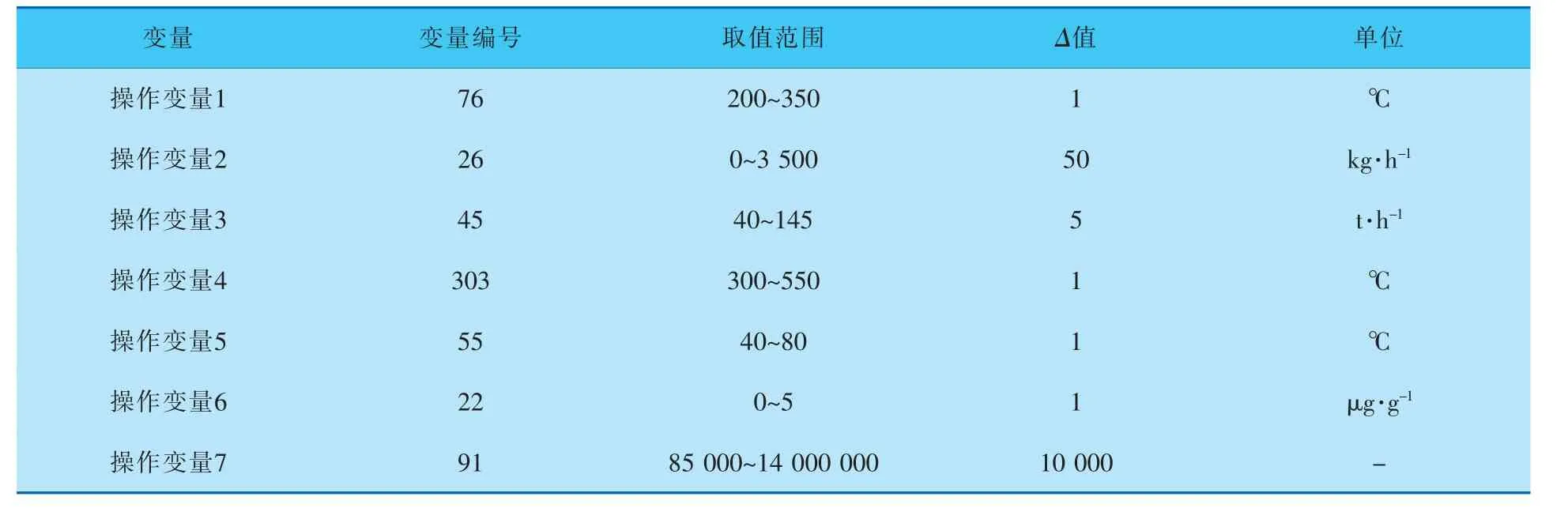
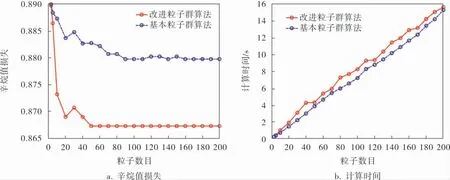
c. 对每个粒子,用它的适应度fit[i]与个体极值pbest比较,如果fit[i] d. 对每个粒子,用它的适应度fit[i]与全局极值gbest比较,如果fit[i] e. 迭代更新粒子的位置Xi和速度Vi; f. 进行边界条件处理; g. 判断算法终止条件是否满足,若是,则结束算法并输出优化结果,否则返回步骤b。 步骤e的更新公式为: 其中,c1、c2为学习因子;r1、r2为[0,1]范围内的均匀随机数,可增加粒子飞行的随机性;vij∈[-Vmax,Vmax],i=1,2,…,N,j=1,2,…,D;Vmax是常数,由用户设定,用来限制粒子的速度。 为了适应真实的生产过程,并提高算法的运行速度,笔者提出了一种改进粒子群算法,几点改进措施如下: a. 修改速度更新公式以适应工艺变量变化的要求,改进后的公式可以保证每次操作变量的变化为一个固定值,这个固定值由实际生产系统决定, 保证实际的生产系统可以实现优化结果。同时,这样设计可以大副减少粒子的数量,提高计算速度。 b. 单独设置每个变量的上限Xmax、下限Xmin和速度Vmax,以符合各个变量的操作范围,省去归一化与反归一化的处理,提高算法速度。 c. 增加边界条件的判断。 由于多个粒子参与优化过程,即使修改速度更新公式,在每一步迭代时工艺变量也会产生剧变,不符合实际生产情况, 所以在每次迭代后增加边界条件的判断,这样可以保证各个操作变量在优化的过程中不会出现剧变的情况,保证在生产过程中操作变量变化的连续性。 d. 增加停止条件。由于改进粒子群算法的特性,原有的停止条件已经不适用于改进粒子群算法,故需新增停止条件,即当gbest在连续5次迭代中没有变化,则优化结束。 改进步骤a的具体公式为: 其中,r1为0或1的随机数;r2为-1或1的随机数;vij(t+1,k)表示下一步第k 个变量的速度;Vmax(k)表示第k个变量每次变化的幅值;xij(t+1,k)表示第k个变量下一步的位置。 改进步骤c中增加的边界条件为: 4.3.1 优化结果 根据实际生产过程,设置每个操作变量的取值范围与单次操作的变化量Δ值(表3),每个操作变量的Δ值决定了判断条件中的Vmax。 表3 操作变量条件 以第106号样本为例, 设置各变量的初始条件(表4)。 表4 变量初始条件 在第106号样本的初始条件下, 设置粒子个数为50个,共迭代13次后得到辛烷值损失的优化结果(图5)。辛烷值损失由最初的1.28下降到最终的0.867 3。 图5 辛烷值损失优化结果 同时,验证算法是否符合真实过程中工艺变量的取值范围与单次操作的Δ值(图6)。 图6 操作变量变化过程 可以看到,操作变量1~7单次的变化均为其Δ值,符合实际生产中变量连续变化的要求。 操作变量6的初始值为实际生产测量所得, 由于测量误差导致该变量的变化不在取值范围内。 4.3.2 与基本粒子群算法对比 改进粒子群算法与基本粒子群算法进行对比,分别选取粒子数目为3,5,10,20,30,40,…,200进行实验,同样取第106号样本。 对改进粒子群算法与基本粒子群算法进行10次测试,将10次测试优化结果的平均值作为优化结果,将10次测试计算时间的平均值作为计算时间,实验结果如图7所示。 图7 改进粒子群算法与基本粒子群算法对比 改进粒子群算法仅需要50个以上的粒子就可以让优化结果趋于一个稳定的数值,而基本粒子群算法至少需要100个粒子甚至是150个粒子以上才可以让优化结果趋于一个稳定的数值。 而更多的粒子就需要更长的运算时间。 在粒子群数目相同的情况下,改进的粒子群算法所需的运算时间仅略高于基本粒子群算法。 综合两方面考虑,虽然改进粒子群算法在粒子数量相同的情况下所需的计算时间略高于基本粒子群算法,改进粒子群拥有更多的判断条件,但是要达到相同的优化结果,改进粒子群算法所需的粒子数量大幅减少,因此极大地提高了寻优速度。 针对汽油辛烷值建模与优化问题,提出了变量筛选-模型建立-优化计算的完整方法。 在变量筛选方面,提出基于随机森林、PCC和MIC的变量筛选方法,并筛选出3个条件变量与7个操作变量作为预测模型的输入变量。 在模型建立方面,提出基于BP神经网络与模糊神经网络的辛烷值预测模型,该模型具有较高的适应性与准确度。 在优化计算方面,提出的改进粒子群算法具有实际应用的潜能。 笔者的研究工作解决了汽油辛烷值优化中, 预测模型输入变量筛选困难的问题、优化算法难以实施的问题,有利于国内原油生产工艺的进一步优化。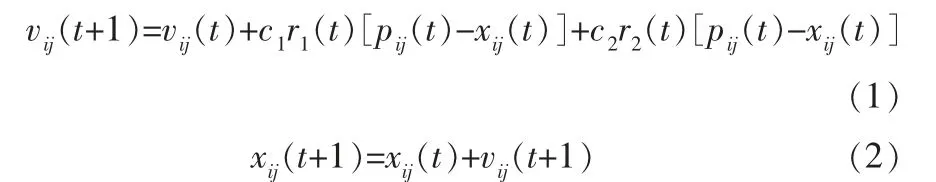
4.2 改进粒子群算法

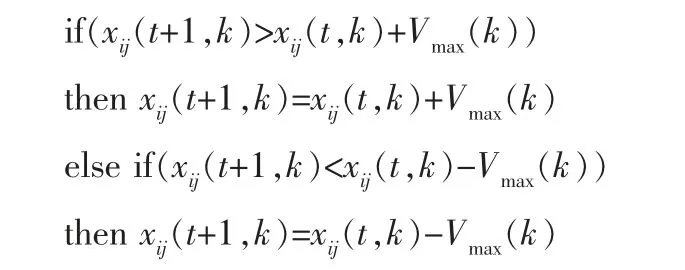
4.3 实验验证


5 结束语
