基于近似最小一乘准则的Hammerstein-Wiener模型随机梯度辨识

徐宝昌 荣志超 王雅欣 董秀娟 许立伟

（1.中国石油大学（北京）信息科学与工程学院；2.国家管网集团北京管道有限公司）

日益复杂的化工过程中存在大量的非线性过程， 线性模型对工业过程的描述能力有限，采用非线性模型描述化工过程，其高质量的建模结果可直接提升化工生产过程的控制品质［1～5］。典型的非线性Hammerstein-Wiener（H-W）模型较适合表示化工过程中的大多数非线性过程。

H-W模型是一种块连接模型，这种通过组合线性动态模块和非线性静态模块的块连接结构模型能够有效地限制模型的灵活性［6～10］。 H-W模型已经成功应用到一些实际过程中，例如太阳能电池板［11］、聚合酶反应器［12］、地埋管换热器［13］、燃料电池反应控制系统［14］及催化系统［15］等。 针对HW模型的辨识，Bai E W提出了两阶段辨识算法和盲辨识算法［16，17］；Zhu Y C提出了松弛迭代法［18］；Park H C等提出用4种特殊信号顺序辨识H-W模型［19］；李妍等提出了一种改进偏差补偿辨识算法［20］；Xu K K等基于极限学习机对H-W模型进行了辨识［21］。 这些算法针对相应的H-W模型都能成功进行参数辨识，但也都存在一定的问题［22～25］，例如：盲辨识算法没有显式考虑广泛存在于实际过程中的噪声；两阶段辨识法和松弛迭代法的计算量都过大；特殊信号法在实际应用中很难使用人为设计的信号；极限学习机很大程度上依赖于初始值。 同时，目前关于H-W模型的辨识算法推导过程大多基于最小二乘准则，但是当随机噪声不满足正态分布（系统存在尖峰噪声或异常点）时，由于其目标函数中的平方项，数据存在很小的改变都会引起较大的波动，对辨识结果产生很大的影响［26，27］。

针对上述问题， 笔者提出一种形式简单、易于计算并且更近似绝对值函数的新型确定性可导函数，构造近似最小一乘准则目标函数，在此基础上推导基于近似最小一乘准则的随机梯度辨识（Stochastic Gradient Algorithm Based on Approximate Least Absolute Deviation Criterion，ALADSG）算法。仿真实验表明，ALADSG算法可以有效克服尖峰噪声对辨识结果的影响，其辨识精度高、收敛速度快并且具有良好的鲁棒性。

1 H-W模型描述

H-W模型的结构如图1所示，其中，g［·］和h［·］分别为系统的输入和输出非线性模块，设输出非线性模块h［·］可逆；G（z）是系统的动态线性模块；u（k）是系统的输入信号；x（k）是输入非线性模块的输出，也是线性模块的输入；w（k）是线性模块的输出，也是输出非线性模块的输入；r（k）是系统的真实输出，与噪声项v（k）叠加后得到系统的测量输出y（k）。

图1 H-W模型结构框图

H-W模型输出可以改写为：

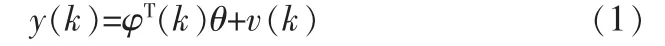
模型参数为：

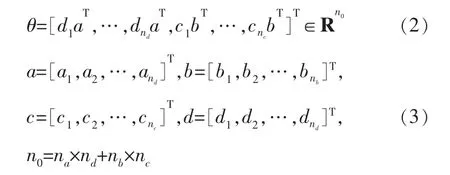
观测数据矩阵为：

其中，φ（k）是观测数据矩阵；θ是待辨识参数矩阵；a、b、c、d是待辨识参数；n是阶次；ψ（k）是输出模块观测矩阵；φ（k）是输入模块观测矩阵；gs和hl分别代表输入模块、输出模块的多项式。

可以观察到在待辨识参数矩阵θ中含有组合参数，为了便于参数分离，令c1和d1已知，采用平均值法进行参数ci和di的分离［28］。

2 ALADSG算法

文献［29］提出了如下的对数函数近似绝对值函数：

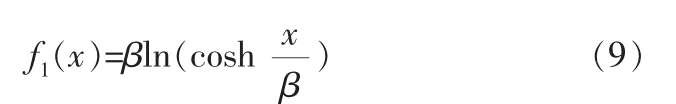
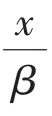
采用另一种绝对值函数的光滑近似函数［30］：

其中，μ是可控参数，当μ比较小时，可有效地等价为绝对值函数，本研究中取μ=0.01。

将f1（x）和f2（x）同时减去绝对值函数｜x｜，x取不同区间时的相对误差见表1。

表1 x取不同区间时的相对误差

由表1可得，函数f2（x）更接近绝对值函数，并且形式简单、计算量更小。 因此，笔者基于函数f2（x）构造近似最小一乘准则。

取目标函数：

根据随机梯度搜索原理可得：

其中，收敛因子μk>0。

将式（12）代入式（13）可得：

将式（14）代入式（11）可得：

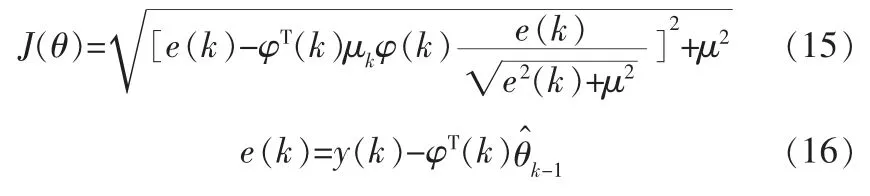
其中，e（k）代表新息。

令：

根据式（17）、（18）极小化h（μk）可得最优解：

将μk代入式（14）可得：

令：

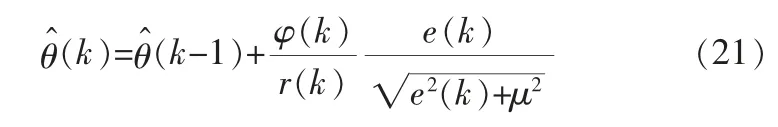
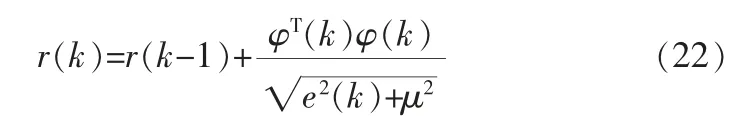
考虑对过去数据的遗忘性，为了加快收敛速度同时提高算法精度，引入遗忘因子λ，则有：

式（21）、（23）构成带有遗忘因子的基于近似最小一乘准则的随机梯度辨识算法， 与选取式（9）作为目标函数得到的算法进行运算速度的对比，均进行30万次迭代，得到的结果见表2。

表2 两种算法的运算时间对比ms

由表2可得，基于式（10）推导的随机梯度算法相较于基于式（9）推导的随机梯度算法计算量更少，速度提升约5.7%。

3 仿真实验

Park H C等研究的pH中和系统［19］如图2所示，V代表容积，其中浓度为0.02 mol/L 的醋酸（CH3COOH） 作为输入流在连续搅拌釜反应器中通过浓度为0.5 mol/L的氢氧化钠（NaOH）滴定流进行滴定。 滴定流分为vm和v，vm为恒定的，v由计算机信号u调节。

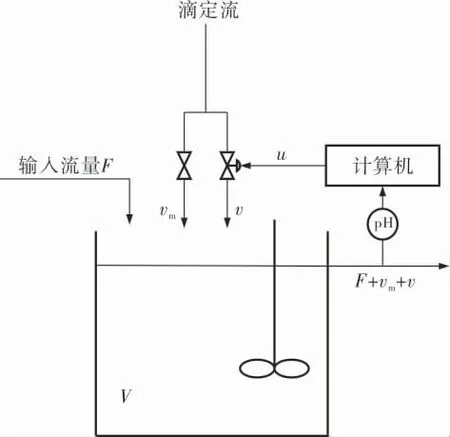
图2 pH中和系统

该pH中和过程可近似建模为H-W模型，其中x（k）和w（k）分别表示为［19］：

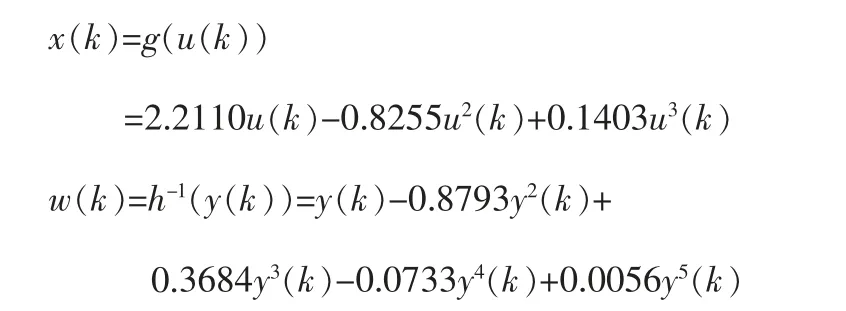
线性模块传递函数为：

为进行参数分离，令参数c1和d1已知。

3.1 不同遗忘因子的ALADSG算法

在模型辨识过程中加入尖峰噪声概率为5%、幅值为白噪声序列5倍的尖峰序列噪声， 不同遗忘因子的H-W模型的参数辨识结果见表3，相对误差曲线如图3所示。

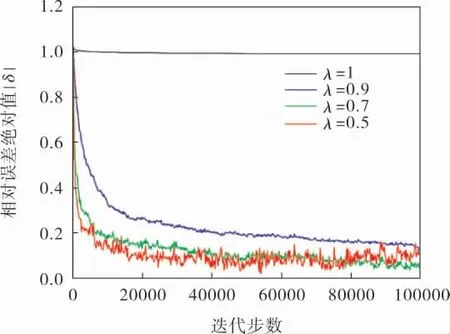
图3 不同λ的相对误差曲线

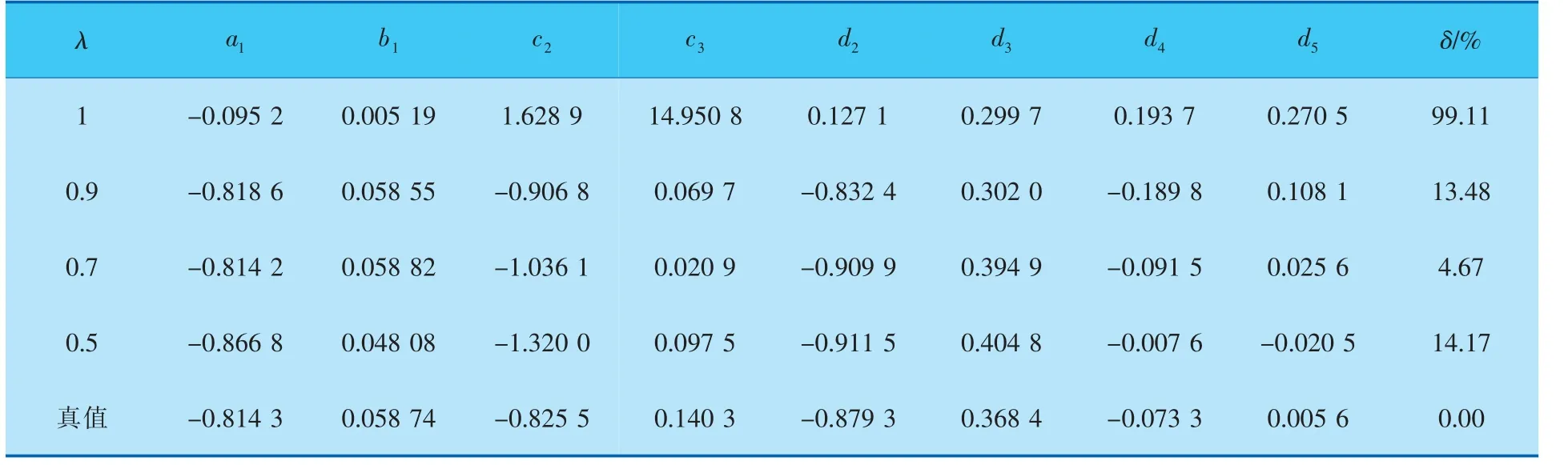
表3 不同λ取值的H-W模型参数辨识结果

根据表3和图3可以得到如下结论：当λ=1时，即不引入遗忘因子，算法的辨识结果较差，无法估计出H-W模型的参数。当0.7<λ＜0.9时，随着遗忘因子λ的减小，δ下降的速度更快，同时辨识相对误差更接近于0，即辨识的速度更快，精度也更高。 当λ≤0.5时，相对误差曲线开始波动，最终辨识结果的精度也已开始下降。 所以不能一味减小λ来寻求更快的辨识速度，而要兼顾精度与稳定性。

3.2 ALADSG算法与LSSG算法对比

由3.1节可知，当λ=0.8时，辨识可以在保证稳定性的前提下收敛，较为准确地估计出H-W模型参数，故本节固定遗忘因子λ=0.8。

为验证ALADSG算法的辨识性能， 分别加入不同概率和幅值的尖峰噪声，同时加入基于最小二乘准则的随机梯度算法 （Stochastic Gradient Algorithm Based on Least Square Criterion，LSSG）作为对比进行实验。 令ε表示尖峰噪声概率，A表示尖峰噪声幅值相对于白噪声幅值的倍数。 在不加入尖峰噪声，加入ε=5%、A=5的尖峰噪声，加入ε=10%、A=10的尖峰噪声，3种情况下得到的仿真结果见表4，对应的相对误差曲线如图4所示。

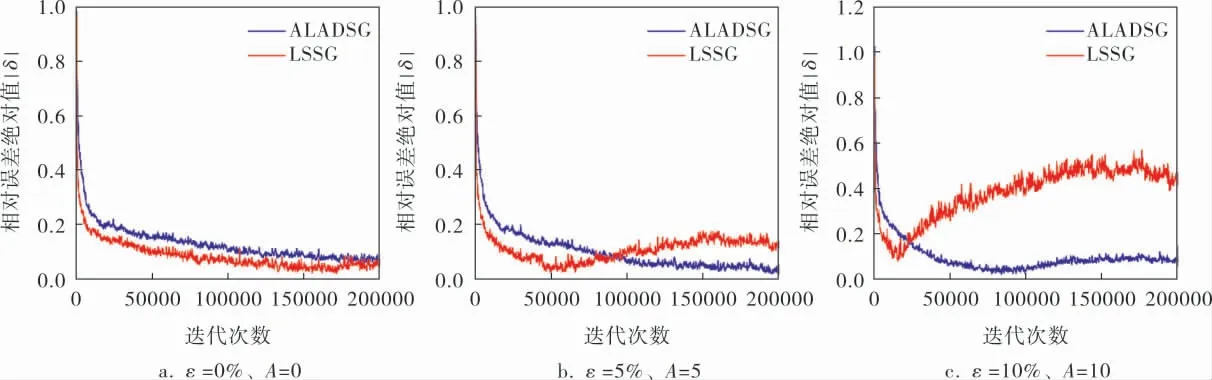
图4 加入不同尖峰噪声时的相对误差曲线

表4 不同尖峰噪声时的仿真结果

从表4和图4可知，当辨识过程中仅存在白噪声时， 两种算法都能准确估计出模型参数，但LSSG算法的速度更快，精度更高。因此，当干扰噪声服从正态分布时，LSSG算法性能优于ALADSG算法，符合以往的研究结论。 在辨识过程中加入尖峰序列后，LSSG算法受尖峰噪声影响较大，辨识精度明显下降，当尖峰噪声概率ε和幅值A较大时已不能精确辨识； 而ALADSG算法受尖峰噪声影响较小，仍然可以保持较高的辨识精度。 说明在存在尖峰噪声的情况下，ALADSG算法性能优于LSSG算法。

4 结束语

H-W模型能够有效拟合化工过程中的大多数非线性过程，且能限制模型的灵活性，避免过拟合的问题。 但当模型辨识过程中存在尖峰噪声时，传统辨识方法不能进行有效辨识。 笔者针对该问题提出了ALADSG算法。 采用一种确定性可导函数近似最小一乘准则，解决了最小一乘准则函数不可求导的问题，降低了计算量。 仿真结果表明， 相较于LSSG算法，ALADSG算法能够有效克服尖峰噪声对H-W模型辨识结果的影响，提高了辨识结果的精度并具有良好的鲁棒性，降低了辨识算法对测量数据质量的要求。 同时，选择合适的遗忘因子可以增加辨识结果的精度、加快收敛速度。