轿车白车身重量目标设定方法

宋光煌

轿车白车身重量目标设定方法

宋光煌

（恒大新能源汽车全球研究总院，广东 广州 511455）

文章探讨了影响轿车白车身重量的因素，包括总质量，车身扭转刚度，长、宽、高等尺寸参数，并通过最佳子集回归分析找到影响轿车白车身主要因素。最后，基于多元线性回归分析，研究最佳影响因素与白车身重量间的关系，并推导出一种用于轿车白车身重量目标设定方法，为项目研发过程中车身重量目标的开发设定提供重要参考。

白车身；重量目标；最佳子集；多元线性回归

前言

汽车轻量化是提升整车性能的重要方向，不仅对汽车的动力性和经济性有着重要影响，而且对汽车操稳、制动、耐久、安全等均有提升[1]。白车身作为占整车重量30%的关键系统，白车身轻量化是实现整车轻量化关键路径。目前，行业内出现了多种评价白车身重量的方法，但主要对尺寸参数进行分析，并均采用一元线性回归分析[2-3]。本文选取了乘用车中的典型车型“轿车”作为分析对象，旨在通过最佳子集回归分析寻找影响白车身重量的关键参数，以及研究各关键因素与白车身重量间的多元线性关系，为白车身重量目标设定和轻量化能提供重要参考依据。

1 影响车身重量因素分析

根据业内车型设计经验，不同车身结构形式，重量也会存在差异，如SUV一般比同平台轿车更重，其他车身材料和承载形式不同也会影响重量。因此，需将其他影响因素排除。本文按照统一的标准选取31款轿车白车身进行分析，具体原则如下：燃油车，承载式车身，2010年后，钢制车身，不含前后防撞梁和油漆辅料的车身。

1.1 性能参数

项目前期需要对整车的基本性能总质量和扭转刚度进行设定，而总质量的大小对安全和耐久都有影响，通常总质量越大，实现同样安全和耐久性能要求的车身就越重，车身扭转刚度也是同样的趋势。因此，将总质量和车身扭转刚度对白车身重量的相关性进行分析。结果如表1，总质量与白车身重量高度相关，相关性达到0.895，而扭转刚度相关性较差，只有0.143。为了方便，将总质量和扭转刚度分别记为1和2，单位分别为kg和kN/rad。

表1 性能与重量相关性

参数总质量A1扭转刚度A2 相关系数0.8950.143

1.2 尺寸参数

众所周知，尺寸参数对白车身重量有着重要影响，尺寸越大，车身重量越大。本节选取了常用的长、宽、高、轴距、前轮距、后轮距进行与白车身重量的相关性分析，各参数分别记为：3、4、5、6、7、8，单位均为mm。从表2结果可知，各尺寸参数除了高5，其他参数对白车身重量相关性较显著，均大于0.689。

表2 尺寸参数与重量相关性

参数长A3宽A4高A5轴距A6前轮距A7后轮距A8 相关系数0.8060.8110.4480.7570.6890.731

1.3 面积和体积参数

选取行业内常用的面积型和体积型参数对轿车白车身重量进行相关性分析。其中，脚印面积9定义为：6·(7+8)·0.5；投影面积10定义为：3·4；三面投影面积11定义为：3·4+3·5+4·5；体积12定义为：3·4·5；名义体积13定义为：[6+(3-6)·0.5]·4·5。其中面积型单位均为mm2，体积型单位均为mm3。从表3的结果可知，面积型参数中，投影面积10与白车身重量相关性最高，达到0.84，脚印面积9与三面投影11相关性略低。体积型参数中，名义体积13与白车身重量相关性最高，达到0.849，体积12与相关性略低。

表3 面积体积参数与重量相关性

参数脚印面积A9投影面积A10三面投影A11体积A12名义体积A13 相关系数0.7820.8400.8370.8350.849

2 关键影响因素最佳子集回归分析

最佳子集回归分析是建立线性回归模型，帮助识别有用的预测变量的自动化工具[4]。上文选取的13个影响轿车白车身重量因素，由于尺寸参数和面积型参数及体积型参数高度相关，无法进行最佳子集分析。因此，需对面积型参数和体积型参数的数量进行优化，保留相关系数最大的投影面积10和名义体积13。最后，将轿车白车身重量作为因变量，1、2、3、4、5、6、7、8、10、13作为自变量，再进行最佳子集回归分析。

表4 关键影响因素最佳子集回归分析

变量R-SqR-Sq（adj）R-Sq预测CpSA1A2A3A4A5A6A7A8A10A13 180.279.577.62.615.873X 172.071.068.614.918.870 X 283.782.580.9－0.614.656X X 283.582.380.5－0.314.736X X 384.983.281.2－0.414.365XX X 384.883.181.0－0.214.418XX X 485.583.380.10.714.331XX X X 485.483.179.30.914.414XX X X 585.682.878.82.514.555XX X XX 585.682.878.02.514.560XX XX X 685.982.375.94.114.735XXXXX X 685.882.375.74.214.761XX XX XX 786.382.275.35.414.794XXX XX XX 786.382.174.05.614.844XX XXX XX 886.481.572.37.315.073XXX XX XXX 886.481.571.07.315.095XX XXX XXX 986.680.969.29.015.341XXX XXXXXX 986.580.867.69.115.381XX XXXXXXX 1086.679.964.411.015.703XXXXXXXXXX

结果见表4，一般R-sq(adj)越大，表明模型拟合越好；R-sq与R-sq (adj)越接近，则表明模型越好；R-sq预测值越大，表明回归方程具有更好的预测作用；接近预测变量数加上常量数的Cp值表明模型在估计真实回归系数和响应时比较精确且无偏倚；S值越小，表明回归标准误差越小。从表4中可知，具有最大的R-sq (adj)的自变量组合是[1、2、6、10]，达到83.3%，同时这个组合的S也是最小的，达到14.331，但它的R-sq预测值偏低，回归方程的预测性稍差。由于，最佳子集分析是进行白车身重量目标设定的重要一步，需要回归方程具有很好的预测性，保证目标设定的合理性。因此，选取R-sq预测值最高的81.2%组合[1、2、10]作为最佳自变量组合，这个组合的R-sq (adj) 83.2%与最大值83.3%差异很小，同样具有显著的相关性，而Cp和S均在可接受范围。

3 白车身重量目标设定方法

3.1 多元线性回归方程推导

通过最佳子集回归分析找到的最佳自变量组合[1、2、10]，轿车白车身重量作为因变量，通过多元线性回归分析推导出回归方程如下：

=−37.6+0.099 5·1+0.017 4·2

+0.000 015·10 （1）

其中为轿车白车身重量。为了更好地用简单一次函数=a+b表示，推导的多元回归方程可改写为：

=−37.6+0 （2）

0=0.099 5·1+0.017 4·2+0.000 015·10

其中0为综合因子，可由1、2、10计算得到。写成简单的一次函数后，方程可以很好地用二维图形表示。

3.2 白车身重量目标设定举例与修正

举例说明，以某新车型参数如表5，根据回归方程得到0：0=0.099 5·1+0.017 4·2+0.000 015·10 =365.6。则新车型轿车白车身重量目标为=−37.6+0 =328 kg。需要说明的是，此时得到的重量目标328 kg只是行业内的平均水平，由于各公司各项目对重量的市场定位不同，对轻量化的要求也不一样，所以可根据得到的平均水平重量目标基础上调整。

表5 新车型参数

参数A1A2A3A4A10 新车型2 0201 2094 4251 8638 243 775

行业内部分公司用简单的方法，对平均水平重量目标进行修正，一般在此基础上进一步优化5%，即(adj)=·0.95。目前，行业通常用LACU表示对目标不同要求，其中L为Leader缩写，即为前10%，领先水平；A为Among the Leaders缩写，即为前10%～30%，领先大部分竞品；C为Competitive缩写，即为30%～70%，有竞争力的；U为Uncompetitive缩写，即为大于70%，无竞争力的。对于轿车白车身重量目标，我们可以采用LACU的方法对重量目标划分区域，以满足不同重量目标需求。

将平行于行业趋势平均线，求解出通过各竞品时趋势线的截距，得到各竞品的截距。通过正态分布的经验累积分布函数，求解10%、30%、70%三个点的值，分别为－51.92、－41.6和－27.31，如图1所示。

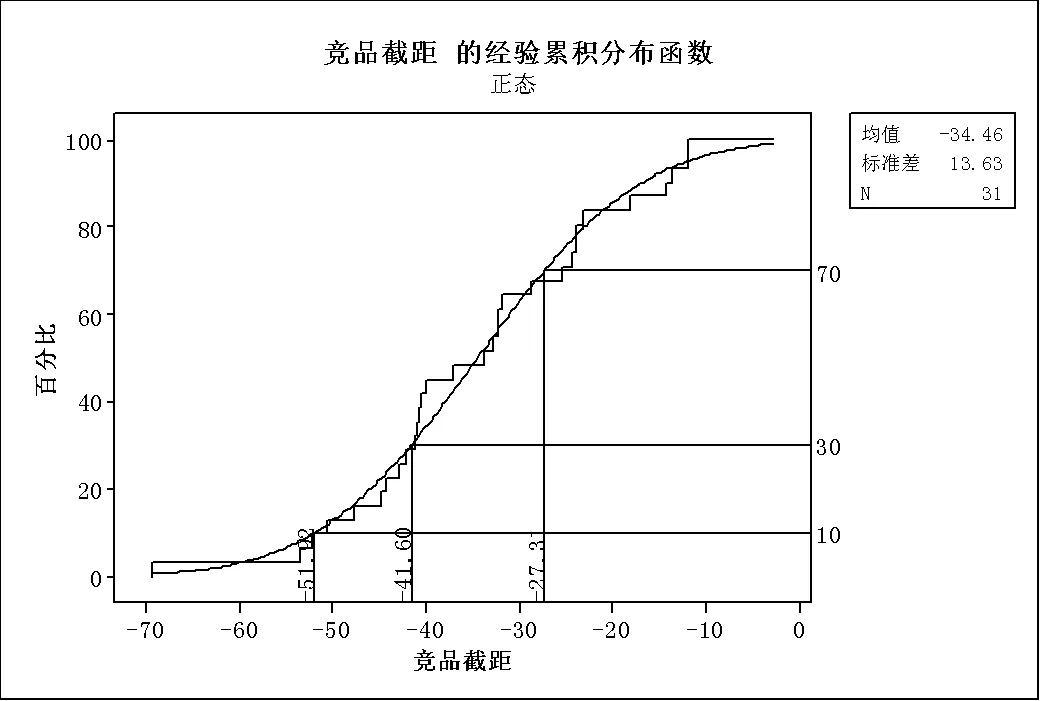
图1 竞品截距LACU分界点

由此得到=－51.92+0之下区域为L，=－51.92 +0与=－41.6+0之间的区域为A，=－41.6+0与=－27.31+0之间的区域为C，=－27.31+0之上的区域为U。如图2所示LACU区域分界，新车型平均重量目标328 kg相当于在Mid-C的水平。根据项目LACU具体的要求，可具体调整新车型轿车白车身重量目标。

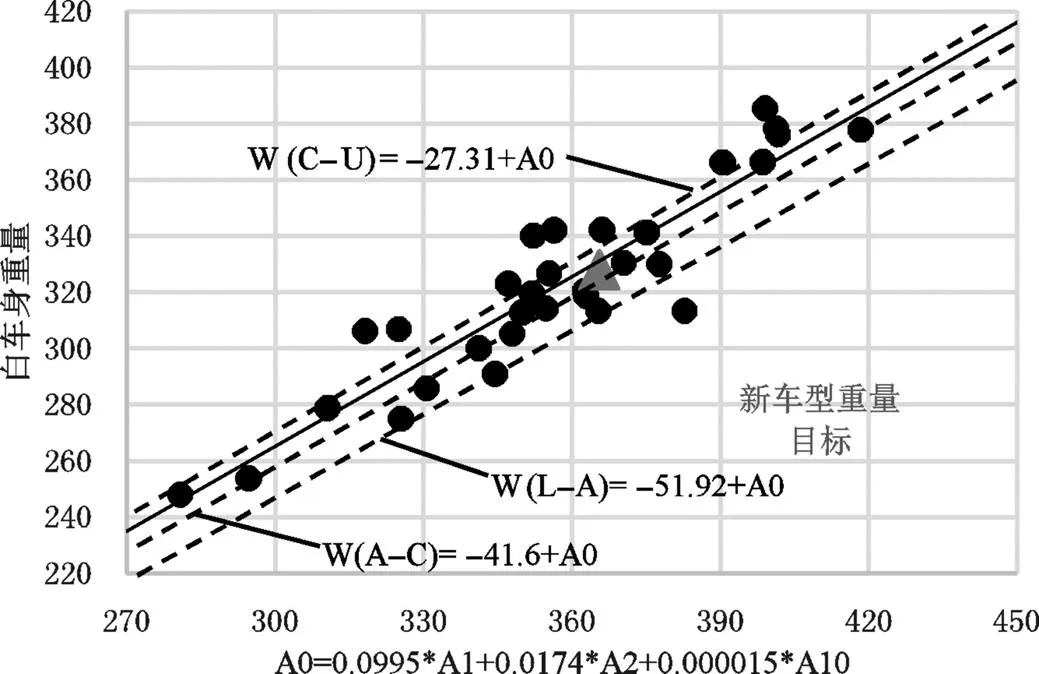
图2 新车型白车身重量回归分析

４ 结论

本文结合行业经验，筛选出13个与轿车白车身重量相关的因素，经过最佳子集分析得到最优的影响因素组合[总质量、车身扭转刚度、投影面积]，最后通过多元线性回归分析得到白车身重量目标回归方程=－37.6+0.099 5·1+0.017 4·2+0.000 015·10。并讨论用LACU市场定位，对轿车白车身重量目标进行修正。该方法对同类型轿车白车身重量目标的设定有很好的借鉴意义。

[1] 严永攀,陈德旺.整车重量管理控制方法的探讨与应用[J].汽车科技,2017(02):72-75.

[2] 路遥,吴强,洪练,等.轿车白车身重量目标设定及优化方法介绍[J].汽车实用技术,2016(05):55-56.

[3] 李文中,王立,李振兴,等.不同尺寸车身轻量化评价及重量目标设定[J].汽车实用技术,2020,45(19):122-124+132.

[4] 梁文骐.一次预报最佳子集回归[J].应用数学学报,1981(04): 356-361.

Weight Target Setting Method for Sedan BIW

SONG Guanghuang

( Evergrande New Energy Vehicles Holdings Limited, Guangdong Guangzhou 511455 )

This paper discusses the factors which affecting sedan BIW weight, including gross vehicle weight, BIW torsional stiffness, length, width, height and other dimensions. It finds out the key factors affecting sedan BIW weight through best subset regression analysis. Based on multiple linear regression analysis, this paper studied the relationship between the optimal influencing factors and sedan BIW weight. Then deduces a method for setting sedan BIW weight target, which provides an important reference for the development and setting of BIW weight target in the project development process.

BIW; Weight target; Best subset regression; Multiple linear regression

A

1671-7988(2022)01-78-04

U463.82

A

1671-7988(2022)01-78-04

CLC NO.: U463.82

宋光煌，硕士，就职于恒大新能源汽车全球研究总院，从事整车重量管理及轻量化方向相关工作。

10.16638/j.cnki.1671-7988.2022.001.018