基于SIR的COVID-19病毒传播动力学仿真研究*
2022-02-15刘家瑞胡彦蓉刘洪久
刘家瑞,胡彦蓉,刘洪久
(浙江农林大学信息工程学院,浙江 杭州311300)
自2019-12-08出现第一例新型冠状病毒肺炎以来,疫情发展十分迅猛。2020-01-11确诊41例,到01-23武汉封城时,全国已出现感染病例830例,死亡25例。此后,不仅是武汉市,全国都进入疫情的快速蔓延时期。最高峰时,02-12新增病例14108例,死亡146人。虽然中国的疫情已得到良好的控制,但到2020-05-21已出现84516个确诊病例,4645人死亡。从世界范围看,由于各国的制度和文化习俗的不同,对疫情的重视程度也不同,2月中下旬,从意大利开始,紧接着西班牙、法国,疫情迅猛发展,席卷整个欧洲和美洲,乃至全世界。目前,疫情最严重的是美国,日新增20000余人,最高峰时接近50000人,截至2020-05-21,美国累计确诊病例1593039例,累计死亡94941人,全世界累计确诊病例5015328例,累计死亡330017人。COVID-19不仅给全世界人民的生命健康带来严重的威胁,也给中国和全世界的经济造成了巨大损失。据专家估计,仅一季度中国经济的损失就高达3万亿元。而亚洲开发银行估计,全球经济损失最高或达8.8万亿美元,相当于全球国内生产总值(GDP)的9.7%。
因此,有必要研究COVID-19病毒的传播规律,研究在不同的防控措施条件下病毒的变化趋势,这对有效预防和控制病毒的二次爆发有积极的意义,同时总结COVID-19病毒的变化特点,对今后研究和预测类似传染病的变化趋势和防控均具有积极作用。
常见的传染病模型有SI、SIS、SIR、SEIR模型[1-3]。最简单的为SI模型,仅考虑易感人群(S)和染病人群(I)两类,SI模型未考虑传染病治愈和死亡的情况。SIS模型考虑了恢复者重新被感染的情况,但在COVID-19传播中未见有治愈病人被重新感染的报道。SIR模型考虑了病愈和死亡的情况。SEIR模型考虑了潜伏状态,但潜伏状态难以发现和估计[4]。综上所述,本文将以SIR模型进行系统动力学模型构建和仿真。
1 数据来源与方法
1.1 数据来源和研究对象
论文的数据均来源于国家、湖北省和武汉市卫生健康委员会的官方网站,由于疫情主要发生于武汉市,因此,本文的研究对象设定为武汉市,相应的干预时间和防疫措施均以武汉市为准。
1.2 SIR系统动力学传播模型
SIR模型包含3类人群:易感者(S)、感染者(I)和移除者(R)。其基本传播动力学方程为[5]:
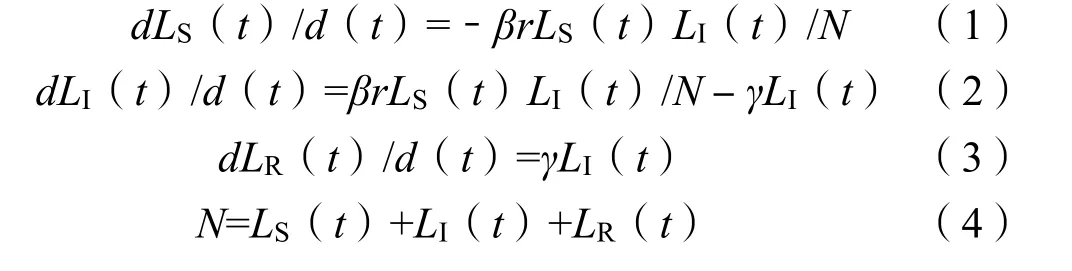
式(1)~(4)中:LS(t)为t时间易感人群的数量;t为时间,d;β为感染率;r为接触人数;N为环境中的总人口数(在一段时间里可认为是常数);LI(t)为t时间感染人群数量;γ为移出率;LR(t)为t时间康复和死亡人群数量[6]。
SIR模型构建的重要基础假设为不考虑出生、死亡和流动因素的影响。原因在于在一个封闭的环境里,相对于人口总数而言,这部分所占的比例很小,且疫情变化的速度比死亡速度要显著的多,故可忽略不计[7]。对于武汉市而言,2020-01-23封城,恰好满足封闭环境的假设。
根据公式(1)~(4)可以构建基本的SIR的系统动力学传播模型,如图1所示。
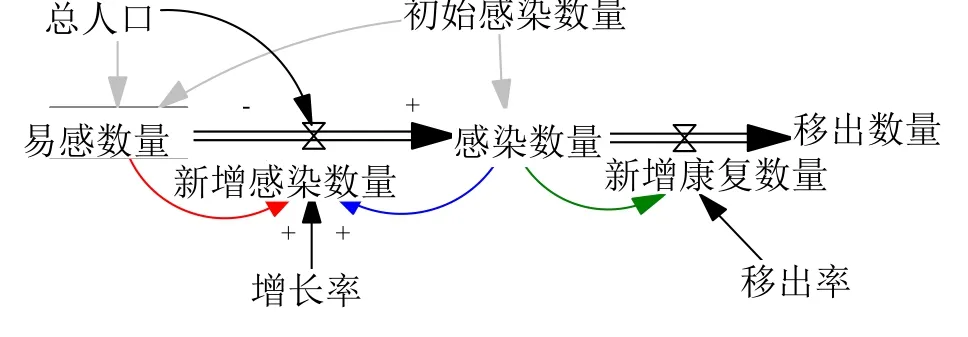
图1 SIR系统动力学传播模型
在传染病模型中,还有一个重要的参数:基本再生系数R0,其含义为单位感染者在感染期内平均传染的人数。当R0<1时COVID-19不会流行,感染者数量LI(t)将会单调下降而趋近于零。当R0>1时,COVID-19将会流行,染病者数量LI(t)逐渐上升而最终发展成地方病。R0=1是作为COVID-19是否消失的界限,意义非常重大[6]。R0可由公式(5)确定:
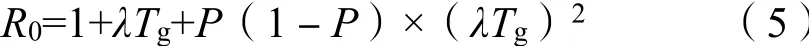
式(5)中:λ为早期感染率,λ=ln(LYt)/t,(LYt)为t时刻的感染数量;Tg为生成时间;P为潜伏期占生成时间的比例。
2 模型仿真和结果讨论
2.1 未采取防控措施条件下
未采取任何防控手段,则疫情处于完全自然传播状态,模型参数和仿真结果如下。
2.1.1 模型参数
人口总数N:根据武汉市2019年国民经济和社会发展统计公报,城镇常驻人口为902.45万。
初始感染数:初始感染数41人,来自于2020-01-15武汉卫健委公布的数据。
感染率β:感染率β为0.0358,根据2020-01-16—2020-03-17的数据(原因在于其后新增病例基本为0),采用最小二乘法求得。
接触人数r:接触人数r为16人,根据新增密切接触人数和新确诊人数之比的平均值,人均密切接触人数约为16。
移出率γ:移出率γ为0.25,根据钟南山院士团队的研究,COVID-19的潜伏期中位数为4d[8],则γ=1/4。
2.1.2 模型仿真
将模型参数代入图1的模型,可得易感数量、感染数量和移出数量随时间变化情况,如图2所示。
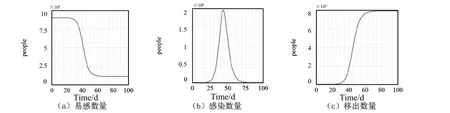
图2 自然传播情况下的仿真结果
从图2(a)中可以看出,自2020-01-15起,85d后易感数量趋于稳定,数量保持在110.6万人,44d后感染数量达到峰值为195.745万人;移出数量在90d后基本达到稳定状态791.8万人,累计确诊人数等于稳定状态的移出数量,同样为791.8万人。可见,武汉市如不采取任何防控措施,到2020-04中旬,累积感染人数将达到总人口数量的87.74%,死亡人数可能达到49.1万人(按统计死亡率6.62%计算),后果将十分严重。
2.2 采取防控措施条件下
发生疫情后,武汉市除封城外,严格限制居民出行,2020-02-10开始规定:居民每户3d只能有1人可以外出,且出行居民均要求戴口罩,洗手、消毒措施均已变成居民常态,这些措施能够有效地降低接触人数,模型参数和仿真结果如下。
2.2.1 模型参数
由于限制出行等措施主要影响接触人数r,根据公开发布的2020-02-10感染人数,将16400人作为初始感染人数,其余参数保持不变。接触人数可以根据武汉市疫情数据采用最小二乘法倒推r=4.5。
2.2.2 模型仿真
同样将模型参数代入图1的模型,可得易感数量、感染数量和移出数量随时间变化情况,如图3所示。
从图3(a)可以看出,自2020-02-10起,50d后易感数量趋于稳定,数量保持在897.8万人;55d后感染数量为94人,下降到100人以下;移出数量在50d后基本达到稳定状态4.544万人,累计确诊人数等于稳定状态的移出数量,同样为4.544万人。仿真结果与湖北省卫健委公布的数据基本相同。武汉市采取强有力的防控措施,武汉市民积极配合,为疫情防护作出了巨大的贡献,到2020-03底,累积感染人数仅占总人口数量的0.55%,死亡人数2553人,仿真结果证实了武汉市采取防控措施的有效性,体现了党和政府的英明决策。
2.3 基本再生系数的仿真
自2019-12-08—2020-01-23,疫情已发生t=47d,则LY(47)=2189(根据2020-02-12修正数据回溯而得),λ=ln(2189)/47=0.1636。根据文献Tg的范围区间为[8.4,10],P=0.7[9],代入公式(5)采用Python进行仿真,可以计算出R0=[2.804,3.246],显然R0>1,新冠肺炎如不加控制会出现大流行,这在欧美国家的表现可以清晰地看到,美国感染数量已近200万人,死亡数量已超10万人,鼓吹群体免疫的英国、瑞典、巴西等国家的防控全部失败。
同样计算出2020-02-10采取严格防控措施后有效再生系数RT的变化。此时λ=ln(28742)/75=0.1636,Tg的范围区间为[2,7],其他参数保持不变,采用Python进行仿真,则RT=[1.291,2.167]。显然,病毒的传染强度大为降低,乐观的情况下已经接近于1,这也是为什么武汉市在3月中旬疫情已基本得到控制的原因。
3 研究结论
新型冠状病毒肺炎的疫情传播不同于一般的传染病,也不同于2013年的SARS的传播,具有极强的致病性和传染性。通过建立系统动力学模型的仿真和基本再生系数R0的测算,可以得出以下结论:①不采取任何防控措施,即采取群体免疫的策略,武汉市疫情爆发后果将极其严重。根据仿真结果,基本再生系数可能超过3.2(有无证感染者存在),如不采取任何措施,2020-02底,感染数量的峰值为195.745万人,到2020-04中旬,累积感染人数将达到791.8万人,占总人口数量的87.74%,死亡人数可能达到49.1万人,武汉市人民的生命健康将受到重创。②严格的防控措施,对疫情在短期内得到控制起到了关键性的作用。2020-02-10开始实施严格的防控措施,使感染人数快速趋于稳定。仿真结果表明,有效再生系数下限接近于1,到2020-04初,感染数量下降到100人以下,累计确诊人数稳定在4.544万人。仿真结果与武汉市卫健委公布的数据基本相符,疫情得到有效控制,真正体现了习总书记“把人民生命安全和身体健康放在首位”的指示。③系统动力学模型能够比较有效地仿真疫情的变化趋势,可以作为疫情预测和控制的依据。SIR系统动力学传播模型能够有效地仿真易感人数、感染人数和移出人数随时间的变化规律,使决策者能够比较清楚地了解不同防控措施下疫情的变化情况,有利于科学决策。
