水位下降条件下边坡稳定性耦合效应分析

万利军,赵兴才,王 盼

(1.宜兴市水利局，江苏 宜兴 214200；2.扬州市勘测设计研究院有限公司，江苏 扬州 225000)

斜坡的稳定性与其几何形状、土体特性以及它受到内部和外部的荷载有关[1]。地表水压力和孔隙压力对边坡稳定性产生影响[2]。在低渗透性土体中，应力引起的孔隙压力和渗流引起的孔隙压力与外部水位变化消散速率不同；在高渗透性土体中，应力引起的孔隙压力大多在水位下降时消散。

水位快速下降会降低边坡稳定性致使边坡破坏[3]。因此，研究和了解发生快速水位下降的水库、河流和湖泊附近斜坡的稳定性，对于保障周围地区的人员和关键基础设施的安全具有重要意义。为了确定边坡的稳定系数，通常采用极限平衡的经典边坡稳定分析或基于有限元法的数值解法。

本文不仅研究了缓慢下降或完全快速下降的极限情况，而且还研究与边坡材料导水率有关的不同水位下降率下的瞬时水位下降情况。为此，采用有限元法对不同的降深率进行了瞬态渗流和变形耦合分析以及稳定性分析。

1 渗流分析

渗流引起的孔隙压力由渗流分析确定。考虑达西定律，多孔饱和不可压缩介质渗流微分方程见式(1)

(1)

式中:φ为总流体势或水头；k为介质的导水率；Q为施加源；S为库容;t为时间。

1.1 有限元公式

有限元方程由式(1)的变分分析得到式(2)

([ks]-[kus]+[ps]-[pus]){q}={Q}

(2)

式中：[ks]为饱和单元的导水率矩阵；[kus]为非饱和单元的导水率矩阵；[ps]为饱和单元的孔隙度矩阵；[pus]为非饱和单元的孔隙矩阵；{q}为节点头向量；{Q}是规定节点流的向量。

将式(2)在时域内积分，自由面可采用迭代格式计算。

1.2 平衡方程

对于饱和不可压缩孔隙流体的两相多孔介质，其平衡方程(3)为

(3)

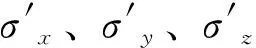
1.3 连续性方程

为了计算各向同性多孔介质固结过程中的流动，采用达西定律采用以下形式的连续性方程(4)：

(4)

式中：εvol为体积应变；n为孔隙度；β为孔隙流体的可压缩性；k为导水率；γw为水的单位重量。

2 有限元分析

为了研究水位下降对斜坡的影响，对以下三种不同情况进行有限元分析。通过有限元分析水位下降，确定了降深结束时的稳定系数，水位下降后的潜水水位如图1所示。

图1 水位下降后的潜水水位

2.1 瞬态渗流分析

在边坡降深模拟中，先进行瞬态渗流分析，得出不同降深率和不同降深比的渗流诱导孔隙水压力和自由地下水面。考虑两个不同的边坡高度和两个各向同性的导水率。通过瞬态渗流分析，模拟水位下降过程中水位变化。计算的地下水流参数(水头、孔隙压力、流速等)用于变形分析。

2.2 变形分析

通过PLAXIS软件进行变形分析，将不排水土模拟为完全饱和的两相连续介质，计算应力引起的孔隙压力和应力应变。假设由土体骨架和孔隙水组成两相连续介质。根据有效应力参数，给出了土骨架的材料参数。

硬化土模型[4]所需的输入参数是众所周知的强度参数，即内摩擦角φ、黏聚力截距c和介电角w。通过三轴试验得出上述刚度参数如图2所示。

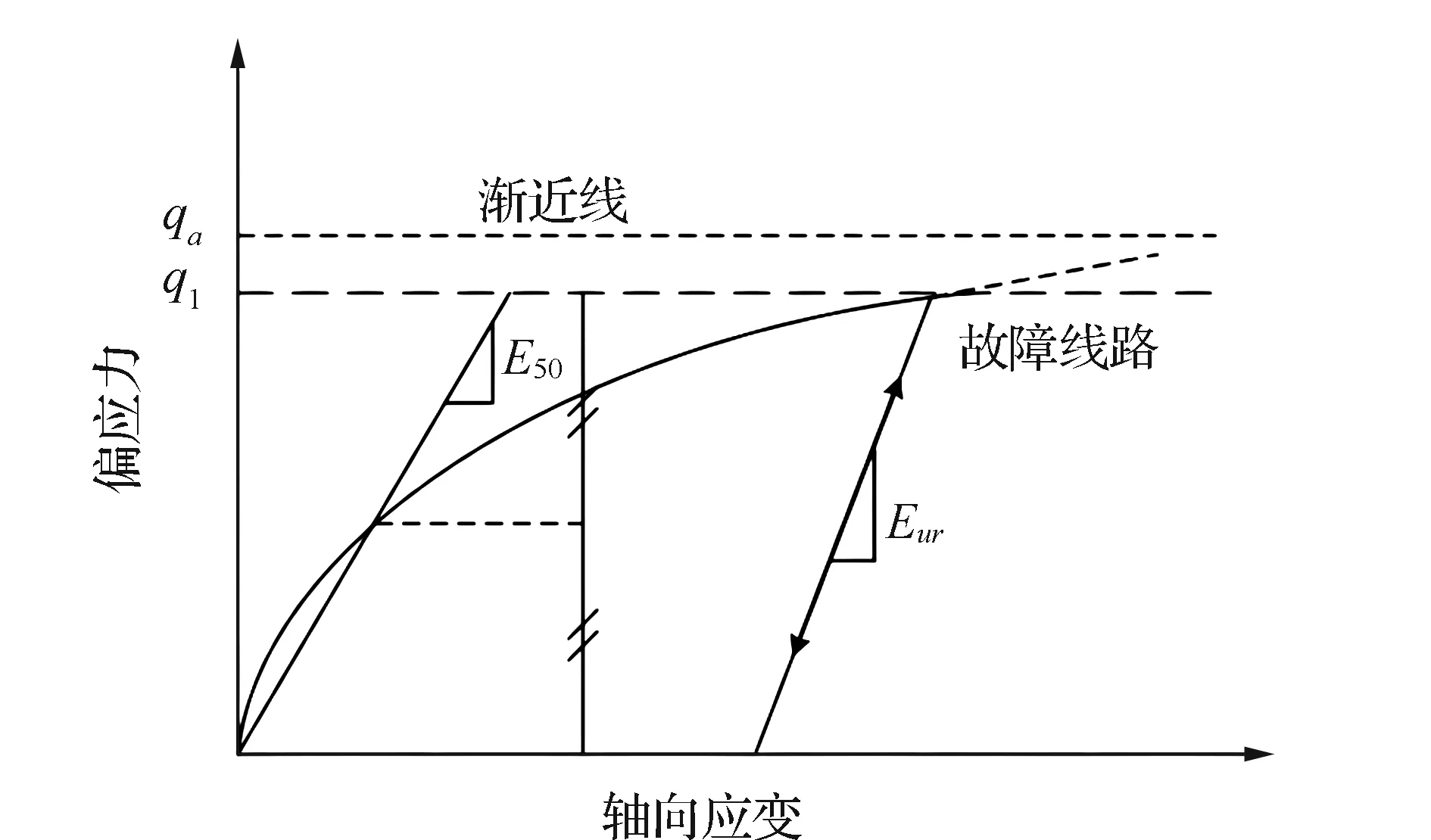
图2 刚度参数

2.3 稳定性分析

通过PLAXIS软件进行稳定性分析，并使用强度折减法。边坡破坏的安全系数是通过将强度参数按一定的速率折减称为强度折减系数∑Msf，在基于莫尔—库仑材料模型的非线性变形分析中，提供平衡的最大∑Msf称为安全系数。

3 分析结果

为了研究浸没边坡在水位下降时的稳定性，采用有限元方法模拟了两种不同的边坡高度H(7 m和14 m)、两种典型的土体导水系数k(10-4cm/s 和10-6cm/s)和两种不同的降深率下的地下水流和边坡变形R(14.0 m/d和0.1 m/d)，五种不同的水位下降率L/H(0.2，0.4，0.6，0.8，1.0)。

在相对较高的土体导水率(k=10-4cm/s)和相当缓慢的水位下降率(R=0.1 m/d)的作用下，即使在水位下降过程中有部分排水，计算出的安全系数(FoS)仍然低于完全缓慢水位下降和高于完全快速水位下降。

对于高水位下降率，如R=1 m/d，即使对于中等渗透性土体(k=10-4cm/s)，边坡行为也接近完全不排水行为，研究表明相当高的导水性土体形成的斜坡，在高水位下降过程中，排水量不大。

比较同一土体但不同高度的两个边坡在水位下降期间的稳定性，对于H=7 m的边坡，FoS为2.67，而对于H=14 m的边坡，FoS=2.02，则计算结果如下：L/H=0，在相同的水位下降率和比率下，提高了坡度的材料特性和FoS值。这是由于强度/应力比(c′/γH)的差异造成的。因此，对于H=7 m高的边坡，100%的水位降深可以实现，但对于H=14 m高的边坡，则不能实现。

根据不同边坡高度、降深率和导水率的分析结果得出图3和图4。FoS随降深时间的变化如图3所示，不同L/H时FoS随不同速率因子(R/k)的变化如图4所示。

图3 FoS随水位下降时间的变化

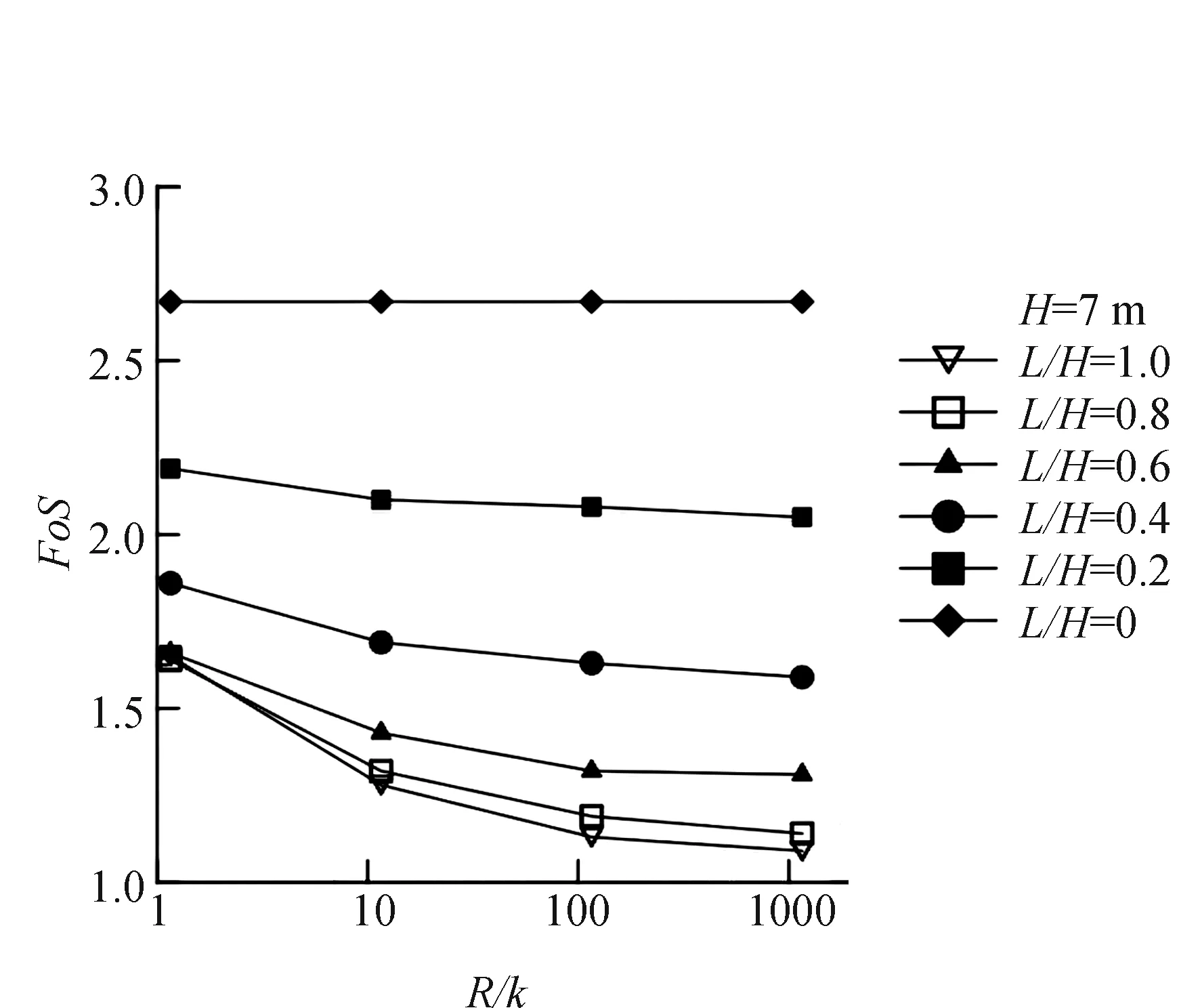
图4 FoS随降深率(R/k)的变化

水位下降期间，由于固结，超孔隙压力会消散，因此可以利用固结时间系数来评估超孔隙压力的水平及其对边坡稳定性的影响[5]。在一维固结中，任何水位下降时间的时间系数T可从式(5)得到

(5)

式中:H为排水路径长度(假设H=L);cv为固结系数。在本研究中，计算任何给定水位下降时间的时间因子。安全系数随时间因素的变化如图5所示。不同水位下降速率下，不同导水率的土体在水位下降结束时的超孔隙压力的变化如图6所示。对于低导水率的土体，不考虑水位下降率，不排水分析更为有效。对于高导水率的土体，在缓慢下降率的情况下，可以假设排水行为，但对于快速下降率(即R=1.0 m/d)，使用的分析方法并不十分清楚。高导水率(k=10-4cm/s)土体中FoS随水位下降率的变化如图5所示，在考虑或不考虑应力引起的孔隙压力的情况下，还显示了耦合固结分析的时间系数T的值。可以发现，对于快速下降率的情况，在相当高的导水率的土体中，完全排水行为的假设似乎是合理的，即使时间系数T>6。在某些情况下，即使T>3，存在未完全消散的超孔隙压力会对抗滑安全产生不利影响，导致FoS值低于完全排水条件下的值，如图6和图7所示。

图5 FoS随时间因子T的变化

图6 极限水位降深L/H=1时标准化超孔隙压力的变化

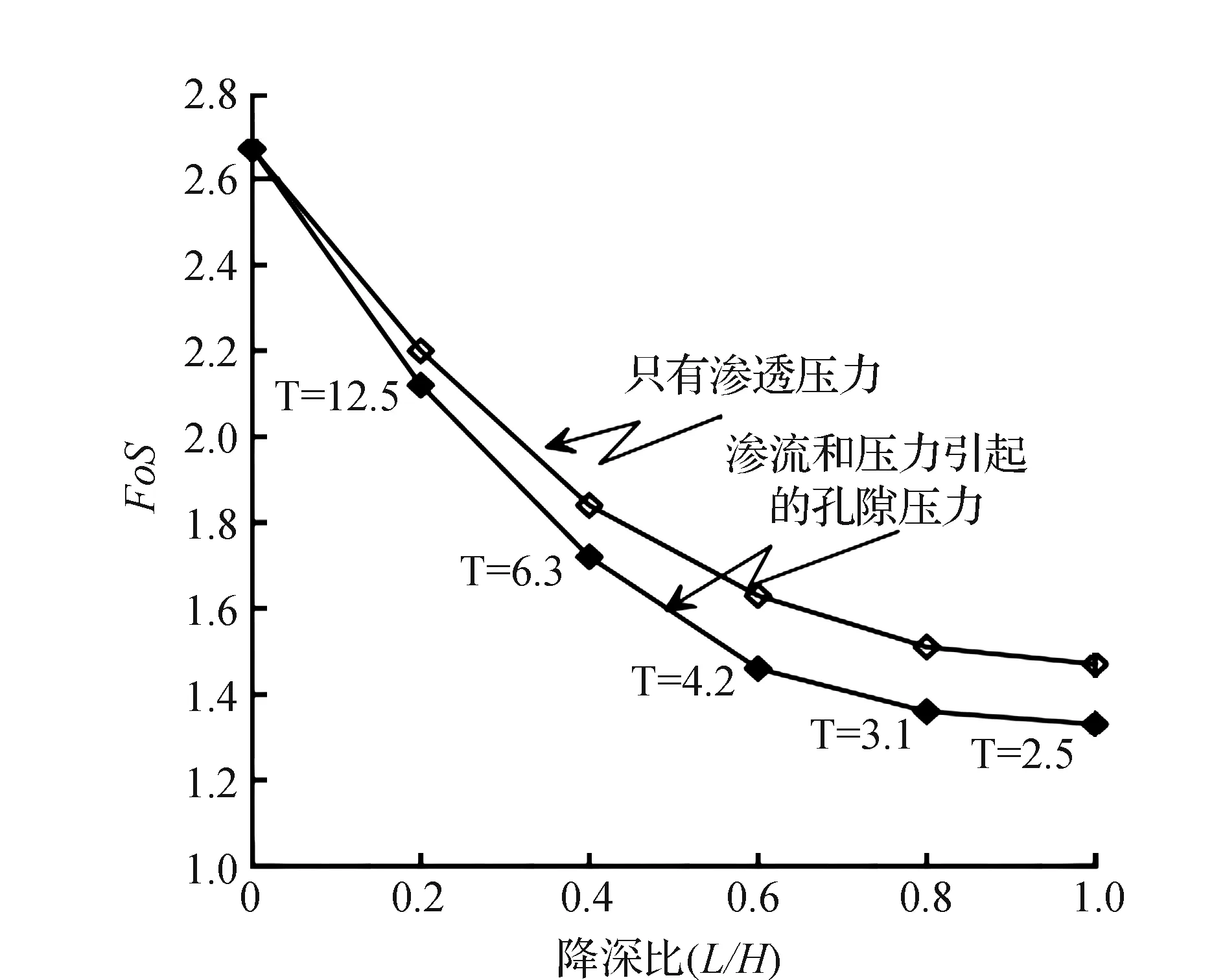
图7 考虑或不考虑应力引起孔隙压力的情况下，FoS随压降比的变化

4 结 论

本文采用瞬态渗流和弹塑性变形耦合有限元分析方法，研究了浸没边坡在水位降落作用下的稳定性，同时考虑了渗流和应力引起的孔隙压力及其消散。通过对结果的分析得出以下结论：

(1)现代数值方法和本构模型能够对瞬态渗流和变形现象进行耦合分析，该方法可以计算渗流和应力引起的孔隙水压力，并可确定边坡内任意阶段的超孔隙水压力分布。因此，可以实际评估边坡在任何阶段的稳定性。

(2)边坡土体中产生的位移量很大程度上受其导水率和水位下降率的影响，并且位移模式似乎高度指示了滑动面。

(3)在相对较高的土体导水率和相当缓慢的水位下降率的情况下，即使在水位下降过程中有部分排水，计算出的FoS仍然低于完全缓慢水位下降和高于完全快速水位下降的情况，H=14 m的差异更大。这种情况不能通过限制性案例进行近似分析。