大倾角、大收缩角泄槽收缩段水流特性研究
2022-02-14肖天培张小飞黄佳敏
肖天培,张小飞,黄佳敏
(广西大学土木建筑工程学院,广西 南宁,530004)
0 前言
工程实践中,受地形、地质、工程结构等因素的限制,泄水建筑物泄槽往往需要布置收缩段,以节省工程量、有利于下游消能防冲。泄水建筑物的下泄水流一般为急流,收缩段内将会产生明显的急流冲击波,从而造成过水断面流量分布不均匀,对收缩段及其下游的流态产生不利影响。目前,收缩段冲击波的计算分析主要基于Ippen提出的理想冲击波理论[1],而该冲击波理论建立于收缩段为平底、小收缩角的条件下。实际工程中,泄水建筑物泄槽通常具有一定的底坡倾角,有些泄槽的底坡倾角甚至大于30°,重力溢流坝下游堰面的直线段的倾角往往在50°~60°之间。
实际工程的应用表明,利用Ippen冲击波理论来计算分析底坡倾角大于30°、收缩角大于15°的大倾角、大收缩角泄槽收缩段水流会产生较大误差。为了计算分析大倾角、大收缩角收缩段水流问题,一些学者进行了初步的探索。刘亚坤等[2]通过物理试验研究了大倾角、大收缩角收缩段水流,试验的收缩段倾角为35°、收缩角为15°、20°,并对Ippen公式进行了修正,但保留了部分和大倾角、大收缩角水流特性不一致的假定,其适用性还需要进一步验证。黄智敏等[3]通过对陡坡收缩段冲击波的理论分析,提出了一种计算边墙沿程水深的方法,但该方法需要进行多次的反复迭代,在工程中应用不便。C.D.Jan等[4,5]对陡坡收缩段水力冲击波特性进行了实验研究,实验的底部倾角范围在27.45°~40.17°之间,侧壁偏转角范围在6.22°~25.38°之间,并提出了冲击角、最大冲击波高度及其位置的经验关系式,而后采用二维水力数值模型,对陡坡收缩段的急流冲击波特性进行数值模拟,验证了其经验关系式的适用性,并扩大了其适用范围。但该经验关系式主要用于计算最大的冲击波高度及位置,而不能反映收缩段边墙沿程水深的变化规律。目前关于大倾角、大收缩角收缩段水流的研究还不够系统全面。
充分认识大倾角、大收缩角收缩段内冲击波的扰动特性,对如何有效削减急流冲击波对泄流的影响、避免发生水流翻越边墙现象,具有重要的工程意义。本文依托FLUENT软件,采用基于RSM湍流模型的三维湍流数值模拟方法,对大倾角(30°~60°)、大收缩角(15°~35°)收缩段的急流冲击波问题开展系统全面研究,分析底坡倾角、边墙收缩角以及来流弗劳德数Fr0对陡坡收缩段水流特性的影响,为更好地解决大倾角、大收缩角收缩段急流冲击波的计算问题提供参考。
1 计算模型的建立及验证
目前,湍流数值模拟方法主要包括直接数值模拟方法、大涡模拟和Reynolds平均法。其中,直接数值模拟方法和大涡模拟对网格精度的要求高,计算量大,因此得到广泛应用的是Reynolds平均法。RSM模型是Reynolds平均法中较为精细的模型。本文研究中的收缩段具有较大的底坡倾角和收缩角,流速较大,收缩段内的水流为湍流,为与之相适应,采用RSM模型模拟湍流流动,同时采用VOF法追踪自由液面,采用有限体积法对控制方程进行离散化,压力-速度耦合方法采用PISO算法,设置时间步长为0.001s。
1.1 基本控制方程
本文采用RSM模型对大倾角、大收缩角收缩段水流进行数值模拟。由于收缩段内水流可视为不可压缩的粘性流体,可运用连续性方程和Navier-Stokes方程来描述。
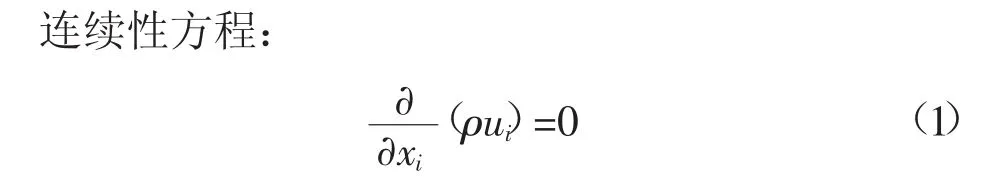

1.2 计算模型的建立
为了系统分析底坡倾角、边墙收缩角和来流弗劳德数对陡坡收缩段水流特性产生的影响,需要建立不同底坡倾角、边墙收缩角的数学模型对泄槽收缩段水流进行数值模拟。各模型主要尺寸见表1和表2。为了保证收缩段有足够的长度,更好地观察边墙沿程水面线的变化规律,将数值模型的入口宽度取为20m;为了使各计算工况下收缩段进口断面的水流相似,都处于均匀流状态,以避免来流流态对模拟结果的影响,使研究结果具有可对比性,在收缩段前设置了与收缩段坡度一致的调整段,调整段长度均取为3m;同时为了减轻水流从水平段进入收缩段时,由于坡度改变引起的跌水对水流流态的影响,参考堰型设计,在水平段和调整段之间设置圆弧段作为平滑过渡。建立的泄槽收缩段计算域模型如图1。

表1 不同倾角模型尺寸表

表2 不同收缩角模型尺寸表
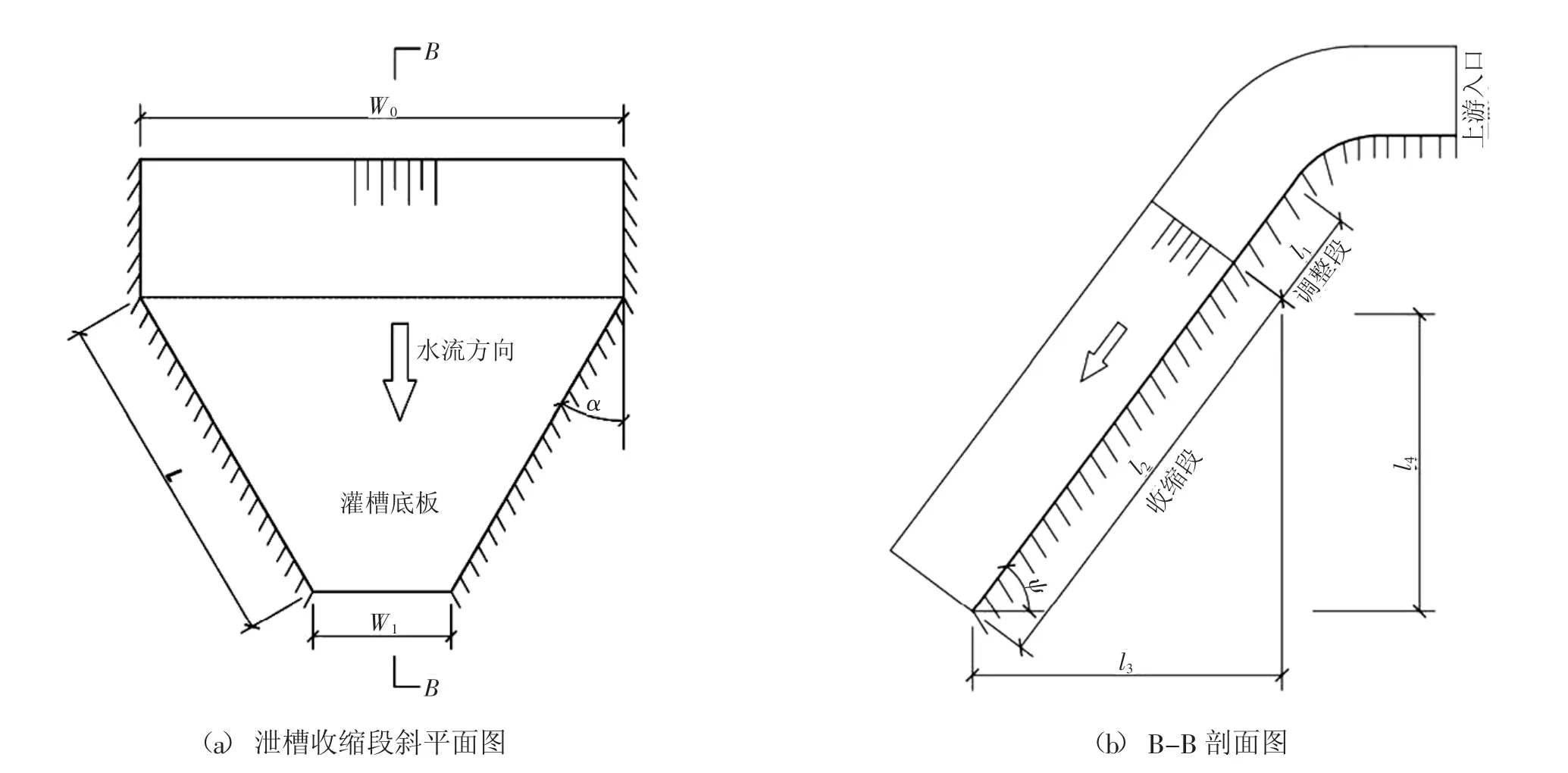
图1 泄槽陡坡收缩段几何模型示意图
由于几何模型同时具有较大的倾角和收缩角,计算区域很不规则,考虑网格对几何模型的适应性,采用四面体网格进行网格划分,使用FLUENT内自带Meshing功能生成网格,同时在底板和边壁处设置了边界层网格。划分的网格如图2,具体网格参数如表3。

表3 网格参数

图2 网格示意图
1.3 边界条件
根据实际情况,给定大倾角、大收缩角收缩段水流数值模拟的边界条件如下:
(1)入口边界条件:液相设置为速度入口边界,气相设置为压力入口边界。本文模拟工况水流在入口处的流量和水深已知,假定数值模型的入口处水流流态均匀,根据流量和水深计算可得到入口断面的流速。
(2)出口边界条件:压力出口边界,在流场出口边界定义静压为大气压强。本文的模拟工况全部为大倾角、大收缩角收缩段水气两相流的流动问题,且收缩段下游出口处水流充分发展,无回流现象。
(3)壁面边界条件:壁面边界包括底坡、边墙等固体壁面边界,壁面对陡坡收缩段内的湍流流动具有很大的影响。在近壁区,由于流体粘性影响,水流雷诺数很小,湍流发展并不充分,一般采用壁面函数法进行处理[7]。常用的壁面函数主要有:标准壁面函数、增强壁面函数、Scalable壁面函数和非平衡壁面函数。由于标准壁面函数法具有应用范围广、经济、精度合理的优势[8],本文主要采用标准壁面函数法。
(4)自由液面条件:对于自由液面的模拟一般有标记网格法(MAC)、体积率法(VOF)和ALE 方法中的网格更新[9]。其中VOF法是目前在数值模拟中应用最广、最成熟的自由液面处理方法,适用于分层流动、自由表面流动、填充、晃动、液体中的大气泡运动、溃坝水流、射流破碎以及任何气—液交界面的稳定或瞬时跟踪。由于大倾角、大收缩角收缩段内的流动为气液两相流,计算域中的水和空气互不相溶,故本文将采用VOF法实现对水气交界面的追踪。
1.4 计算模型验证
参考何飞龙完成的大倾角直线边墙收缩段的试验研究[10],建立和文献[10]物理试验模型一致的数值模型,对其部分工况下的陡坡收缩段水流进行仿真数值模拟,并将计算所得结果与试验结果进行对比分析,验证所建立的大倾角、大收缩角收缩段水流的数值模型的可靠性和计算精度,模拟的工况见表4。

表4 数值模拟工况
1.4.1 流态对比验证
选择0.051 3m3/s工况下陡坡收缩段水流流态进行对比分析。图3~图4为0.051 3m3/s时陡坡收缩段数值模拟结果与试验流态对比。泄槽内整体的水流流态与试验中观察到的流态基本一致。水流进入收缩段后,受到边墙收缩的影响,与边墙交汇的水流与边墙发生碰撞,方向发生突变,水流沿边墙跃起,在紧邻边墙区域产生较显著的水面壅高,形成水流冲击波,水流冲击波具有狭窄的局部波动面,扰动线与边墙之间的夹角△β=β-α很小,β为冲击波波角,而△β反映了冲击波的影响范围。与边墙有一定距离的水流未受到冲击波的影响,水流流态与无收缩段溢流坝的相似。

图3 流态对比

图4 收缩段边墙水流对比
图4为收缩段边墙处模拟结果与试验流态对比。试验和数值分析结果均表明:由于越靠近边墙的水流越先与边墙交汇、碰撞,并沿边墙跃起,而越远离边墙的水流越后与边墙交汇、碰撞、跃起,先交汇跃起并沿边墙向下流动的水流在边墙的上部运动,而后交汇的水流则在边墙的下部运动,边墙处上部水流由于重力作用不会一直壅高,又因为受到下部水流的向上顶托作用,无法发生回落,因此,随着水流的行进,边墙处水深逐渐趋于稳定。边墙处各股水流不发生相互混掺,形成了明显的分层现象。
1.4.2 沿程水深对比验证
陡坡收缩段内高速水流掺气严重,即使采用VOF方法追踪自由液面也很难确定掺气水面高度,本文将水和空气的体积分数各为50%处作为水气交界面,得到扣除气体后的实际水深。以调整段和收缩段的交界面,即收缩段起始断面为进口断面,从收缩段进口断面至出口断面的中线沿程水深、边墙沿程水深的数值模拟计算值与试验实测值见图5、图6。从图中可以看出,试验和模拟结果吻合良好,两者的沿程水深数值最大差值在0.02m左右,相对误差绝对值均在2%以内。
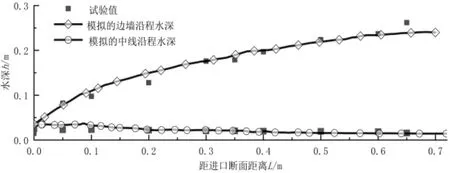
图5 0.051 3m3/s时的沿程水深
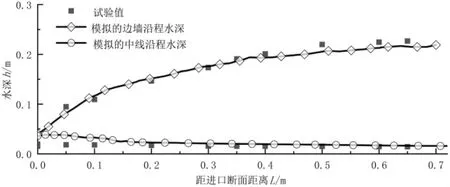
图6 0.038 9m3/s时的沿程水深
1.4.3 流速对比验证
选取四个典型的控制断面的波后水流进行测量,断面距进口断面距离(沿边墙方向)分别为L=0m、L=0.05m、L=0.35m、L=0.65m,其中,L=0m为收缩段进口断面。针对试验设置的各测点位置,提取数值模拟结果中相应位置处的平均流速,与试验实测数据进行对比验证,在通过流量为0.051 3m3/s和流量为0.038 9m3/s时结果见表5和表6。由表中数据可以看出,采用RSM湍流模型模拟得到的平均流速与试验实测值相比较,最小相对误差1.2%,最大相对误差3.8%,均在允许范围内。
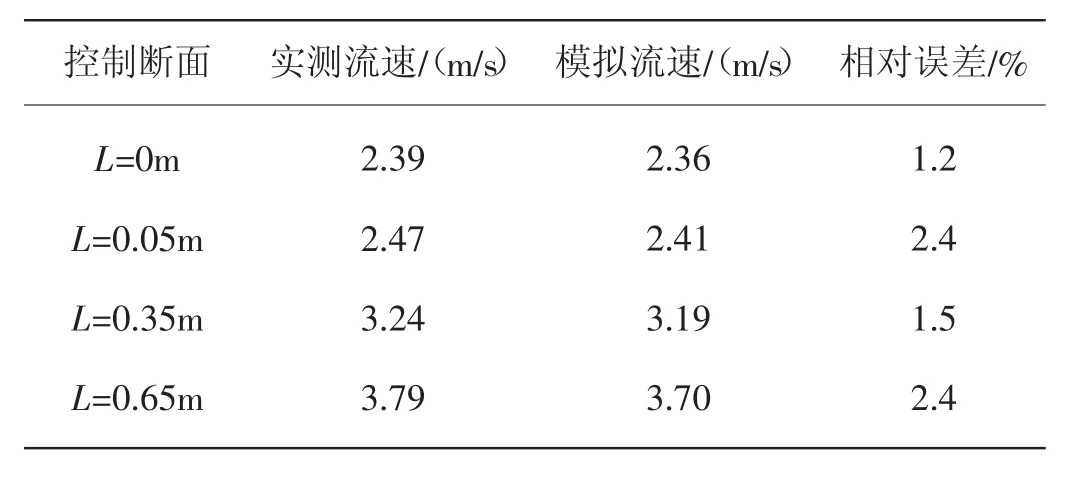
表5 0.051 3m3/s下各断面波后流速模拟值与试验值对比
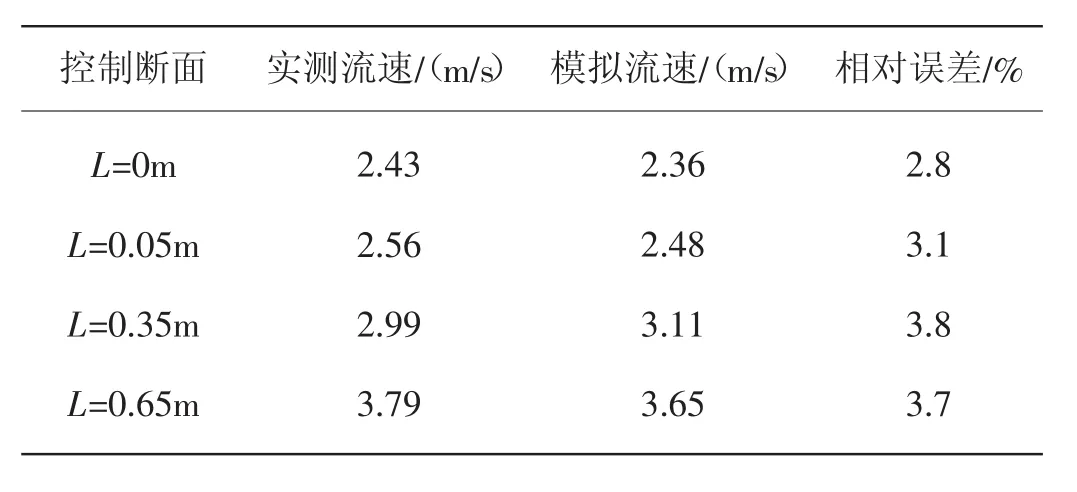
表6 0.038 9m3/s下各断面波后流速模拟值与试验值对比
根据以上三个方面对比结果,综合分析说明:所采用的数值模拟方法可靠,RSM模型能够很好地模拟大倾角、大收缩角收缩段的水流特性,并且网络划分能够满足计算精度的要求。
2 倾角和收缩角对收缩段水流特性的影响分析
2.1 底坡倾角对收缩段边墙沿程水深的影响分析
为深入研究底坡倾角与收缩段水流特性的关系,对底坡倾角ψ 分别为 30°、40°、50°、60°四种模型的收缩段水流进行数值模拟。四种底坡模型的边墙收缩角均为30°。各计算工况的模型尺寸见表1,共计算了60m3/s、90m3/s、120m3/s、150m3/s四个流量。四个流量时收缩段的水流特性相似,限于篇幅,所有工况只选取流量为120m3/s、入口边界水深为2m、相应的入口流速为3m/s的情况进行分析。计算得到各工况相应的收缩段进口断面水力参数见表7,由于调整段的存在,随着底坡倾角的增大,收缩段进口断面的弗劳德数Fr0也将略微增大。
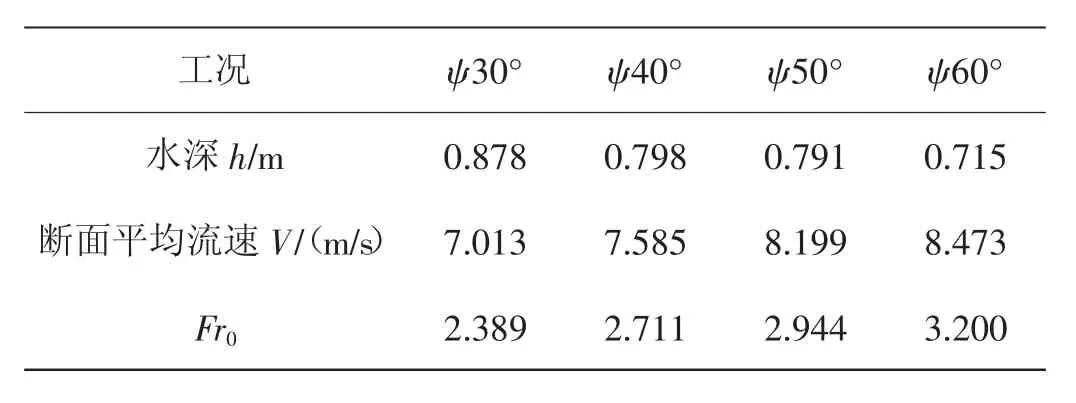
表7 收缩段进口断面水力参数
图7是底坡倾角为60°、流量为120m3/s时收缩段水深h=0.3m位置流速分布及流线图,图8是边墙处流线及流速矢量图,图9和图10分别为流量120m3/s时不同底坡倾角下收缩段的中线、边墙沿程水深。可见,和流量为0.051 3m3/s时的流态相似,流量为120m3/s时边墙收缩产生的冲击波主要是向下游传播,横向影响范围很小。水流在与边墙交汇时发生碰撞、跃起,并沿收缩边墙向下游流动,先与边墙碰撞跃起的水流位于上部,后与边墙碰撞跃起的水流位于下部,流线基本没有发生交叉,水流分层明显,水面线则呈现出“先快速升高,后逐渐平稳”的趋势。底坡倾角越大,水深由急速壅高开始转变为平缓升高的位置更靠近下游。倾角为 30°、40°、50°、60°时,与收缩段进口断面水深相比,L=14m处的边墙水深壅高依次为5.89倍、8.23倍、10.59倍、12.62倍。表明在收缩角相同时,倾角越大,边墙壅水水深越大。
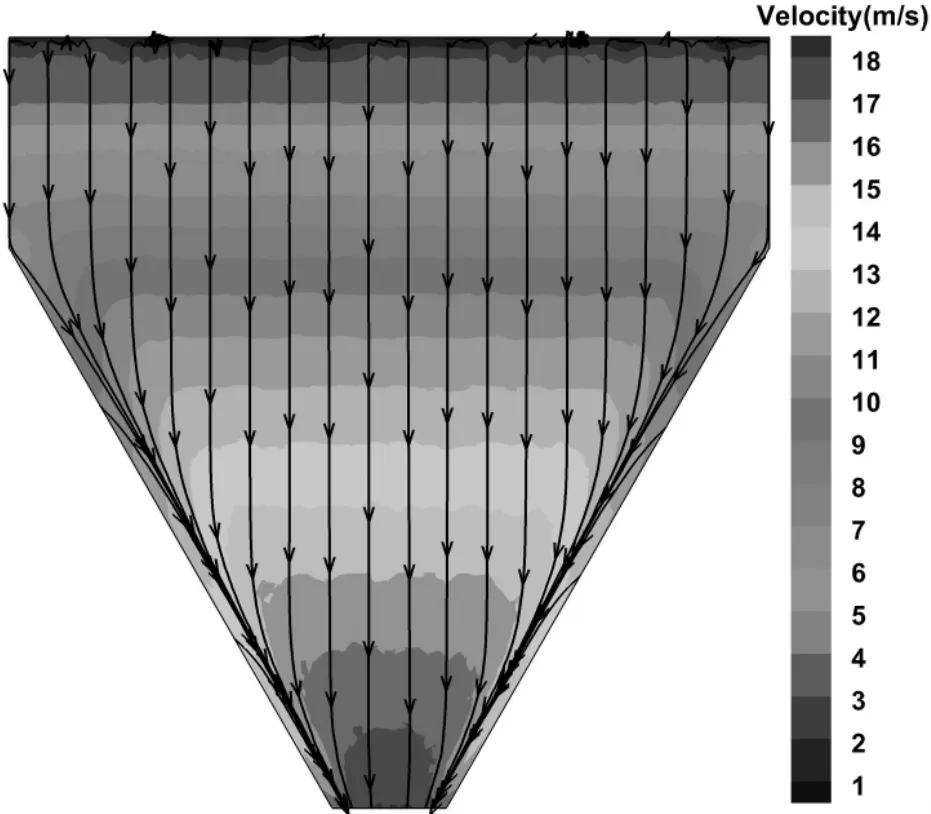
图7 h=0.3m位置流速分布及流线
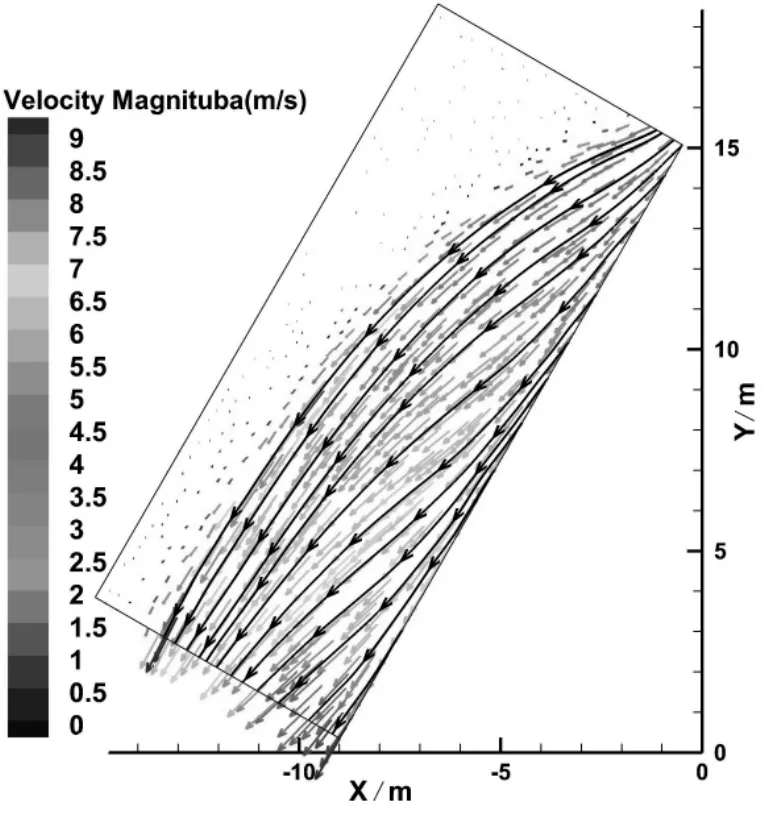
图8 边墙处流线及流速矢量
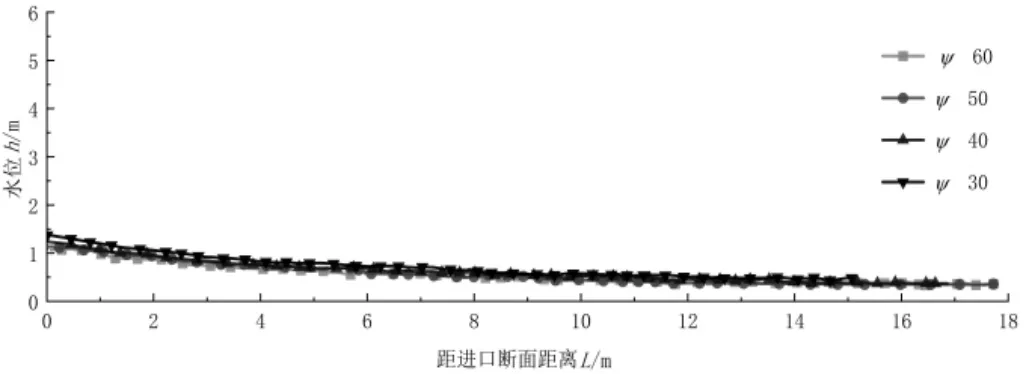
图9 中线处沿程水深
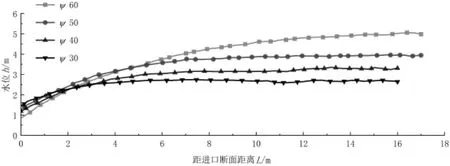
图10 边墙处沿程水深
2.2 边墙收缩角对收缩段边墙沿程水深的影响分析
为系统研究边墙收缩角与收缩段水流特性的关系,对底坡倾角为 60°、边墙收缩角 α 分别为 15°、20°、25°、30°、35°的五种收缩段水流进行数值模拟。各不同收缩角模型的尺寸见表2,计算模型的边界条件和2.1相同。计算得到各模型工况相应的收缩段进口断面水力参数如表8。
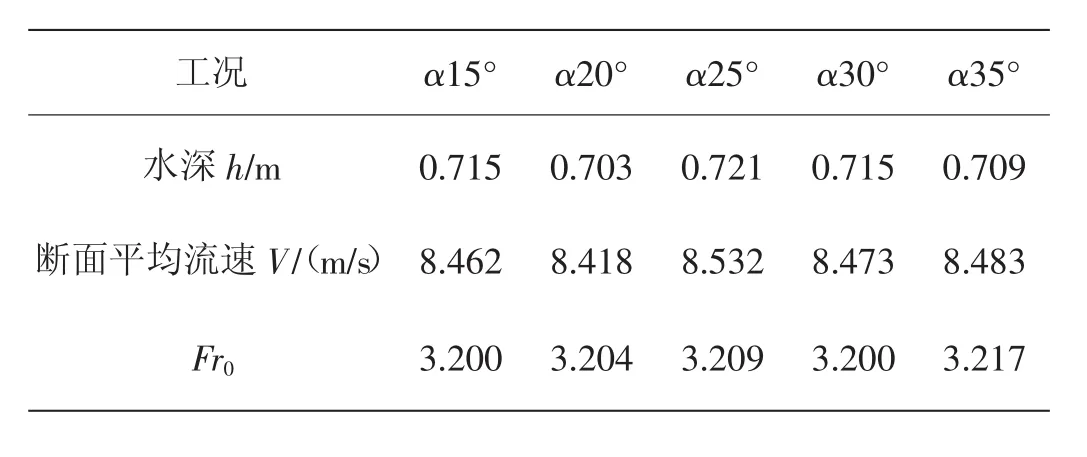
表8 收缩段进口断面水力参数
图11为底坡倾角为60°、流量为120m3/s时不同收缩角下收缩段边墙沿程水深变化图,收缩段的中线附近的水流不受收缩段产生的冲击波的影响。不同收缩角下,陡坡收缩段边墙处的水流流态和2.1表述的相似,沿程水深均呈现“先快速升高、后逐渐平稳”的变化规律。当收缩角分别为 15°、20°、25°、30°、35°时,与收缩段进口断面水深相比,边墙水深在L=14m处依次壅高为5.85倍、7.55倍、9.97倍、12.62倍、16.3倍。在底坡倾角相同时,收缩角越大,边墙壅水水深越大。
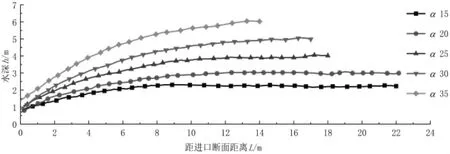
图11 边墙处沿程水深
2.3 来流弗劳德数对收缩段边墙沿程水深的影响分析
为了研究来流弗劳德数对陡坡收缩段内水流特性的影响,对流量Q分别为60m3/s、90m3/s、120m3/s、150m3/s四个工况的陡坡收缩段进行数值模拟,数值模型的底坡倾角均为60°,边墙收缩角均为30°。设置上游入口边界水深分别为1m、1.5m、2m、2.5m,流速为3m/s。计算工况如表9所示。计算得到各工况相应的进口断面水力参数如表10。
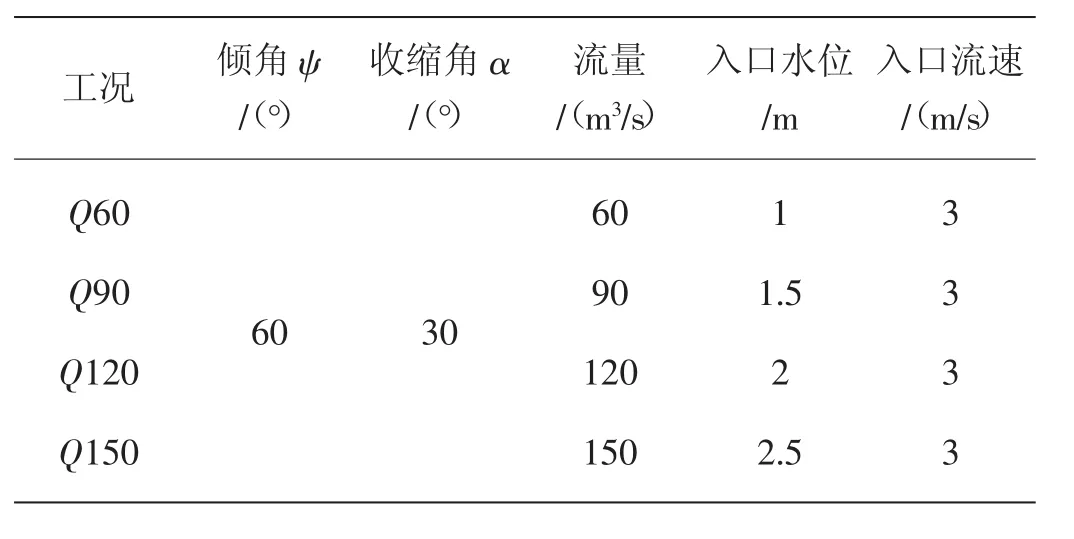
表9 计算工况设置
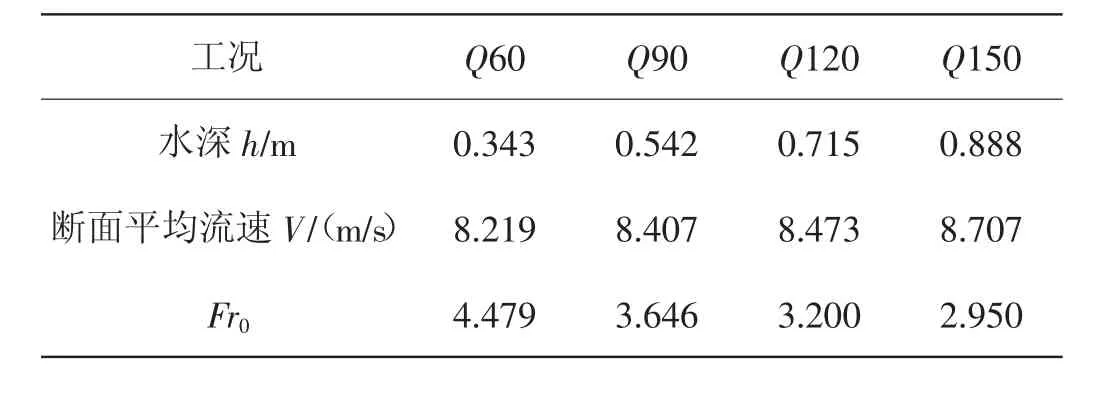
表10 收缩段进口断面水力参数
各工况下收缩段边墙处沿程水面线如图12所示,当底坡倾角、边墙收缩角一定时,来流弗劳德数减小,相同落差时边墙水深明显增大,来流弗劳德数Fr0分别为4.53、3.20、3.65、2.95时,与收缩段进口断面水深相比,边墙水深在L=14m处依次壅高为20.89倍、16.99倍、13.68倍、11.16倍。
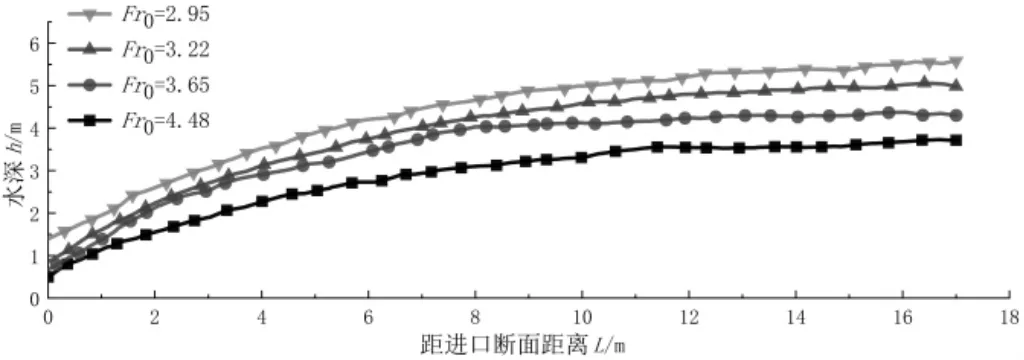
图12 边墙沿程水深
3 结论
本文依托FLUENT软件,基于RSM湍流模型,对大倾角、大收缩角泄槽收缩段水流进行数值模拟,系统分析了在大倾角、大收缩角条件下,底坡倾角、收缩角以及来流弗劳德数对收缩段水流特性的影响,得到了以下结论:
(1)大倾角、大收缩角情况下,水流进入收缩段后,受到边墙收缩的影响,在紧邻边墙区域产生较显著的水面壅高,形成水流冲击波,水流冲击波具有狭窄的局部波动面,扰动线与边墙之间的夹角△β=β-α很小,冲击波的横向影响范围很小。
(2)在大倾角、大收缩角条件下,水流在与边墙交汇时发生碰撞、跃起,并沿收缩边墙向下游流动,先与边墙碰撞跃起的水流位于上部,后与边墙碰撞跃起的水流位于下部,流线基本没有发生交叉,水流分层明显,水面线则呈现出“先快速升高,后逐渐平稳”的趋势。
(3)在相同收缩角的条件下,来流流量一定时,底坡倾角越大,边墙附近壅水水深越大;底坡倾角和来流流量一定时,收缩角越大,边墙附近壅水水深越大;当底坡倾角、边墙收缩角一定时,来流弗劳德数减小,相同落差时边墙处水面壅高越大。
