纳米尺度下偏心圆柱形芯-壳结构对平面压缩波的多重散射研究

王 琴，欧志英

(兰州理工大学理学院，兰州 730050)

芯-壳结构复合纳米颗粒[1]因其独特性、多样性及可调性等优异性能得到广泛生产和使用，并引起了纳米材料和界面科学工作者的极大兴趣。据文献记载，不同频率下的表面效应对动应力集中因子的影响显著，但缺少偏心芯-壳结构的研究。芯-壳结构复合纳米颗粒在构造过程中，结构内外无法保证绝对同心，存在偏心结构的情况。从一些文献中可以看到，在多重散射作用下，表面效应等微观尺度性质影响的偏心圆柱形芯-壳结构的动态力学特性研究尚不充分。为填补这一空白，研究了偏心圆柱形芯-壳结构复合纳米颗粒的表/界面动力学问题，结果表明，表面效应对动应力集中因子的影响十分显著。

1 模型与公式

1.1 模型建立

建立如图1所示的模型。考虑全空间下嵌入两个距离为2d的偏心圆柱，每个圆柱的外圆半径为a2/b2，内圆半径为a1/b1，两圆心之间的距离为h，L1和L2分别表示涂层与基体、涂层与芯体之间的界面，基体、涂层和芯体的弹性常数和密度分别为λ(i)、μ(i)和ρ(i)(i=1,2,3)。参照全局坐标系(x,y)，为方便起见，在每个圆的中心设置一个局部坐标系，并假定XOY平面上的平面应变满足σzz=v(σrr+σθθ)。

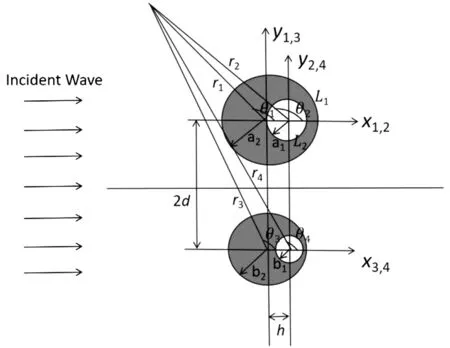
图1 纳米尺度下偏心圆柱形芯-壳结构对入射P波的多重散射Fig.1 Multiple scattering of eccentric cylindrical core-shell structure on incident wave in nanoscale

1.2 波在不同坐标系下的基本方程

假设随时间变化的平面压缩P波沿着X轴的正方向入射，入射波可以在局部坐标系中直接表示为：

(1)

当入射波撞击纳米尺度下偏心圆柱形芯-壳结构时，P波和SV波分别从L1界面散射出来，由此引起的散射波相应的位移势为：

(2)

(3)

在纳米尺度下偏心芯-壳结构1中，根据叠加定理，由式(1)、式(2)和式(3)可得到基体中的总弹性场：

(4)

(5)

为方便计算，需统一坐标系，故使用Graf加法公式进行多极坐标之间的转换：

(6)

(7)

将式(6)和式(7)分别代入到式(4)和式(5)中，可以得到：

(8)

(9)

同理，偏心圆柱形芯-壳结构2中基体的总波场形式如下：

(10)

(11)

受到涂层外边界L1的折射和涂层内边界L2的散射，通过叠加原理，偏心圆柱形芯-壳结构1和2中涂层内的波函数为：

(12)

(13)

由于涂层中的波函数位于不同的坐标系下，因此使用外域的Graf加法公式进行坐标系下的转换：

(14)

(15)

把式(14)、式(15)分别代入到式(12)、式(13)中，可以得出在局部极坐标系，涂层中的波函数形式分别如下：

(16)

(17)

(18)

(19)

芯体介质内产生的折射波在局部坐标系(r2,θ2)和(r4,θ4)可表示为：

(20)

(21)

1.3 边界条件求解

由广义的Young-Laplace方程，可以得到应力和位移边界条件为：

(22)

(23)

(24)

(25)

其中，si(i=1,2,3,4)为无量纲量，表示纳米尺度下所具有的表面效应。

将平面问题中的位移和应力表达式代入到上述位移和应力边界条件(22)～(25)，得到关于待求参数Anη，Bnη，Cnj，Dnj，Enj，Fnj，Gnη，Knη(η=1,3;j=1,2;n=0,1,2…)的线性方程组，通过求解线性方程组，得到确定的位移场和应力场。

由于结构具有对称性，可只考虑纳米偏心圆柱形芯-壳结构1上的界面L1周围的波的动应力集中情况。现将边界L1处的动应力集中因子DSCF定义为全波在某一点上产生的应力与入射波(未受障碍)在同一点上产生的应力的比值，并表示为：

(26)

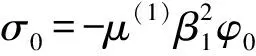
1.4 结果分析与讨论

考虑在纳米尺度下不同频率入射波作用时的具有理想界面的偏心圆柱形芯-壳结构间的相互作用问题，发现动应力集中因子与表面效应有关。

图2表明，当稳态入射波以低频入射，表面效应s2对动应力集中因子影响显著，总体趋势是随着表面效应s2的增加，在纳米尺度下偏心圆柱形芯-壳结构界面L1处的DSCF的值反而减少，并在整个范围内关于Y轴对称，随着角度的变化，DSCF值也呈现明显的周期性，并均在θ=±π/2处取到最大值。

图3表明，当稳态入射波以高频入射，表面效应s2对动应力集中因子影响与低频入射情况大不相同的是，由于散射现象起着主导因素，DSCF的值在纳米尺度下偏心圆柱形芯-壳结构界面L1处变得敏感，分布复杂，且出现多个峰值，但是总体趋势是随着表面效应s2的增加，DSCF的值在整个范围内减少。其中，在θ=±π/2范围内时，变化明显，并在θ=0处，DSCF取得最大值。

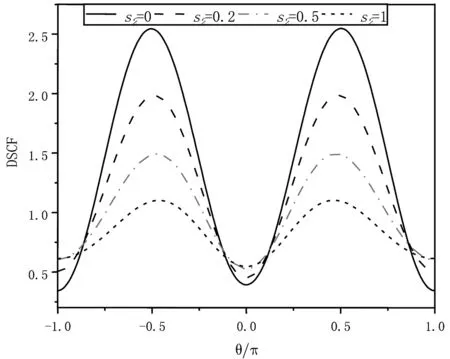
图2 波数α1R2=0.1下，表面效应s2对DSCF的影响Fig.2 Influence of surface effect s2 on DSCF in wave number α1R2=0.1

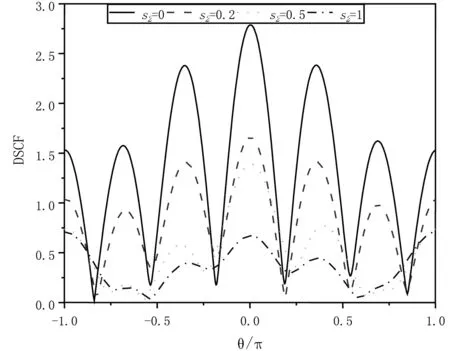
图3 波数α1R2=2下，表面效应s2对DSCF的影响Fig.3 Influence of surface effect s2 on DSCF in wave number α1R2=2

2 结论

基于表面弹性理论，研究了纳米尺度下具有理想界面的偏心圆柱形芯-壳结构对平面P波的多重散射问题，先将波动方程中的边界问题转化为包含波函数中未知系数的无穷代数方程组求解，再用DSCF来刻画偏心圆柱形芯-壳结构表面的动应力集中因子。研究表明，无论是低频波还是高频波入射，当偏心率e固定时，在软夹杂中，其表面效应倾向于抑制表/界面处的DSCF值，因此在复合纳米材料界面的加工和设计方面需要引起重视。