基于投影法的三维流场数值求解方法

骆佳玲，李伟忠，王文全*,3

(1.昆明理工大学 建筑工程学院，云南 昆明 650500；2.昆明理工大学 冶金与能源工程学院，云南 昆明 650500；3.四川大学 水利水电学院，四川 成都 610065)

投影法是数值求解N-S(navier stokes)方程的一种十分有效的方法，最初是由CHORIN[1]在1968年提出的，在之后的发展过程中不断得到改进，得到一系列的改进后的投影格式，使其求解精度得到了极大的提高，例如，常怀见[2]构造了一种基于非结构网格的求解非稳态流动的高精度数值算法，时间和空间的收敛精度达到了二阶以上。胡锐锋等[3]提出了具有四阶空间精度的不可压缩流动的投影格式。浸入边界法中采用固定的笛卡尔网格，且在求解中不需要更新网格，在变形大的流固耦合问题计算中具有很大的优势,所以投影法和浸入边界法的结合受到了很多研究人员的关注。王文全等[4]在传统的投影法基础上发展了一种投影浸入边界法，提高了计算的精度。TIAN等[5]利用有限元法和投影浸入边界法三维数值模拟了大变形的流固耦合问题，研究了其在生物流体力学中的具体应用。李宇航[6]在投影法与直接力浸入边界法结合的基础上修正体积力，研究了仿飞蛇滑翔平板的空气动力学机理。

在N-S方程求解中，压力泊松方程(Poisson equation)的数值求解是难点之一，常用的数值求解方法有迭代法和直接法。二维Poisson方程具有五点差分格式[7]，可利用直接法进行求解，三维Poisson方程的差分格式在有些文献[8]中进行了一般性的介绍，文献[9]中也给出了具体的三维Poisson方程的七点差分格式, 但是其精度及其实用性没有得到验证。二维Poisson方程可利用直接法进行快速稳定的求解[10]，但是三维问题得到的线性方程组相对于二维情况变得很大，这对求解方程组的数值方法和计算机的存储都具有很大的挑战。

为此，本文运用七点差分格式并结合迭代法原理，将三维的数值求解简化为二维的数值求解，结合方程组求解的迭代求解法和直接求解法，建立投影法的三维数学模型和数值求解策略，对三维问题进行快速稳定的求解。采用VC++编写投影法的数值计算代码，通过求解三维数值算例验证了三维压力Poisson方程数值方法的求解精度和准确性，并以三维槽道流场为基准数值算例，验证了三维压力Poisson方程数值计算结果的可靠性和适用性。

1 数值计算方法

1.1 控制方程

流体为黏性不可压缩流体时，张量形式的控制方程表示如下[11]，

▽ui=0

(1)

(2)

式中，ui,uj为速度矢量；p为压强；Re为流动雷诺数。

1.2 时间推进和对流扩散项的离散方法

利用投影法对方程(1),(2)进行分步求解，基本步骤如下：

(3)

式中，C表示对流项；V表示黏性扩散项。在求解方程(3)时，对C和V的数值离散化，参照文献[10]中二维的数值离散化，将其直接推广至三维问题。

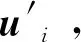
(4)

式中，pn+1表示下一时间步的压力值，可由压力泊松方程求出，

(5)

求解(5)式时使用Neumann边界条件，

(6)

1.3 三维泊松方程的数值求解方法

在整个数值求解计算过程中，求解三维压力Poisson方程是关键也是难点。我们考虑一长方体区域，在x、y、z方向上分别划分为M、N、P等份，三个方向上的网格间距分别为Δx、Δy、Δz。利用标准的七点差分格式空间离散三维Poisson方程，即：

(7)

将包含z方向变化的数值项视为已知数，移至等式右边整理得，

(8)

第一时间步内分别在各个xy平面上进行直接迭代求解，后续时间步内不用迭代法，右端项的压力项采用上一时间步的值用直接法直接求解，边界内部采用中心差分格式离散，详细的边界处理步骤见文献[10,12-13]。

离散化后，通过整理可以得到与二维同阶的大型稀疏方程组，表示如下：

AP=D

(9)

式中，

P=[P0,j,k,P1,j,k,…,Pi,j,k,…,PM-1,j,k,PM,j,k]T

Pi,j,k=[pi,0,k,pi,1,k,…,pi,j,k,…,pi,N-1,k,pi,N,k]T，i=0,1,…,M

D=[D0,j,k,D1,j,k,…,Di,j,k,…,DM-1,j,k,DM,j,k]T

在每一次对大型稀疏线性方程组的求解时，k为常数，是二维求解问题，k值在[0,P]上变化。流场在时间上推进过程中，只需要在t=0～Δt的第一步求解时进行迭代求解，可以减小因多次迭代求解产生的误差累积，通过解+1次线性方程组，三维问题就可得到求解。

2 数值算例

2.1 三维泊松方程的数值求解验证

为了验证1.3节提出的三维Poisson方程数值求解方法的有效性和准确性，考虑Ω={(x,y,z)|0≤x≤1,0≤y≤1,0≤z≤1}内的数值边值问题，函数的表达式及其边界条件表示如下：

(10)

函数u(x,y,z)的解析表达式如下，

u(x,y,z)=sin(xπ)cos(yπ+π/3)cos(zπ+π/4)

(11)

如图1所示为x=0.5,z=0面上不同网格划分下计算精度的比较，网格数划分大于50×50×50数值结果与精确解相一致。精确解与数值解以及它们的相对误差见表1，可以发现随着网格数量的增加，计算结果与精确解的误差减小。

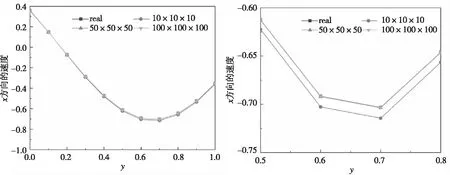
图1 不同网格划分下数值解与精确解的结果比较

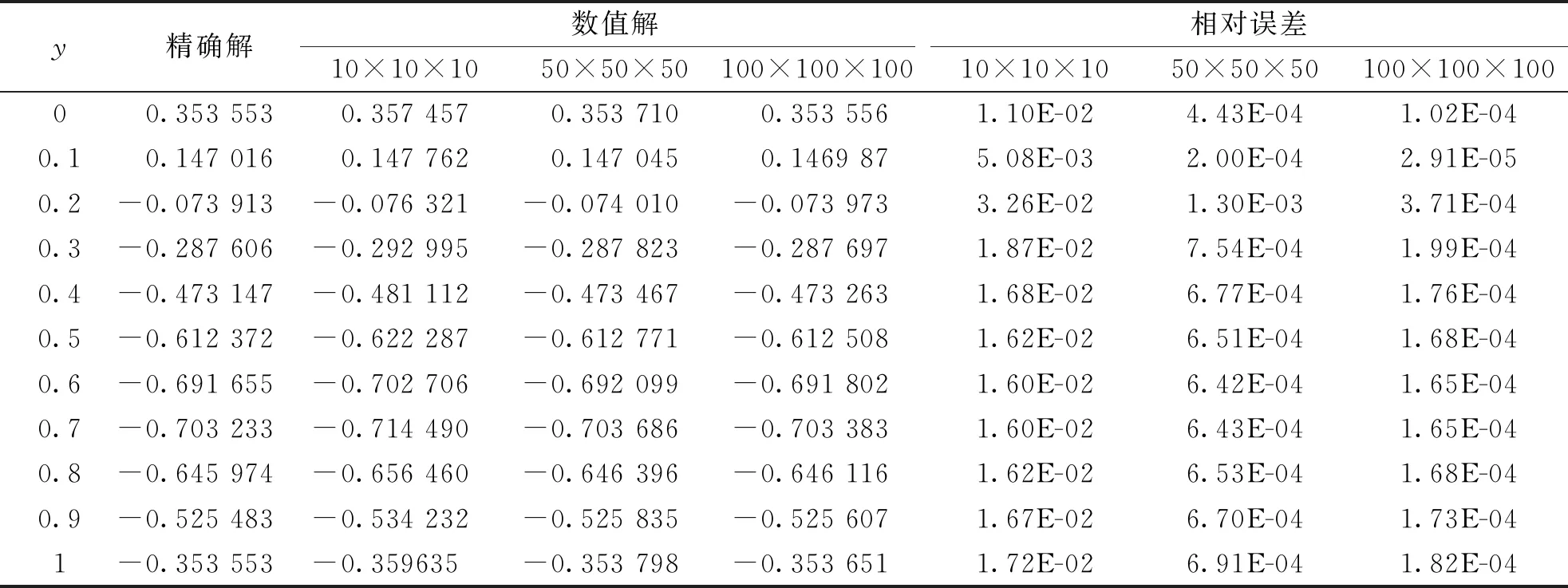
表1 截面x=0.5,z=0处不同网格划分下数值解与精确解以及相对误差之间的对比

2.2 三维槽道流动

计算域和边界条件如图2所示，左面为速度入口，使用Dirichlet压力边界条件[4]，右面为出口，上下左右四个面为固体壁面，使用Neumann压力边界条件[4]，网格步长为Δx=Δy=Δz=0.025，时间步长为Δt=0.001。

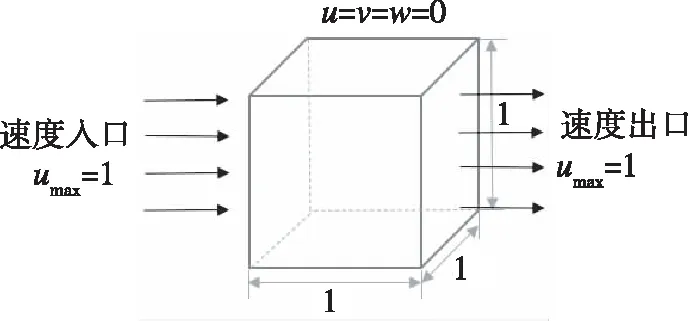
图2 计算域及边界条件

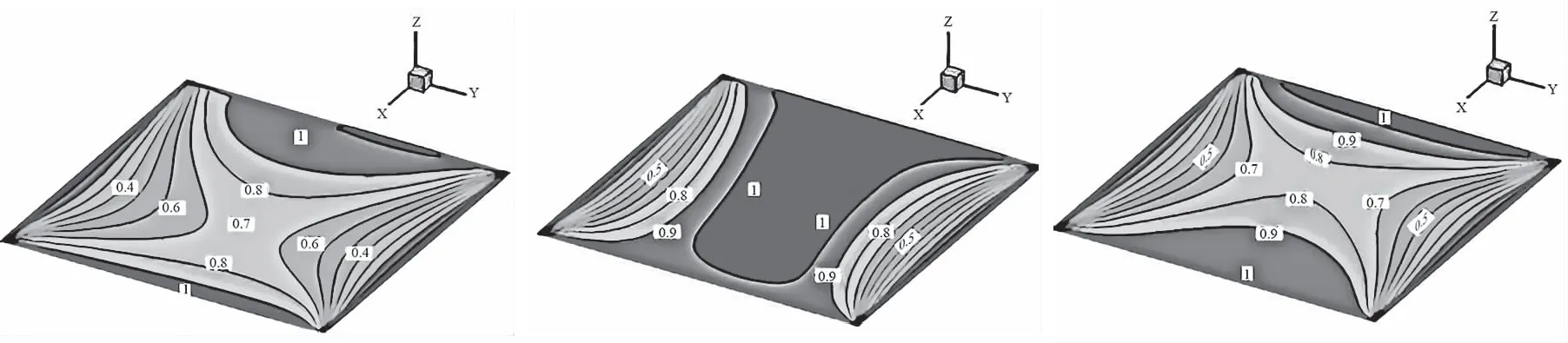
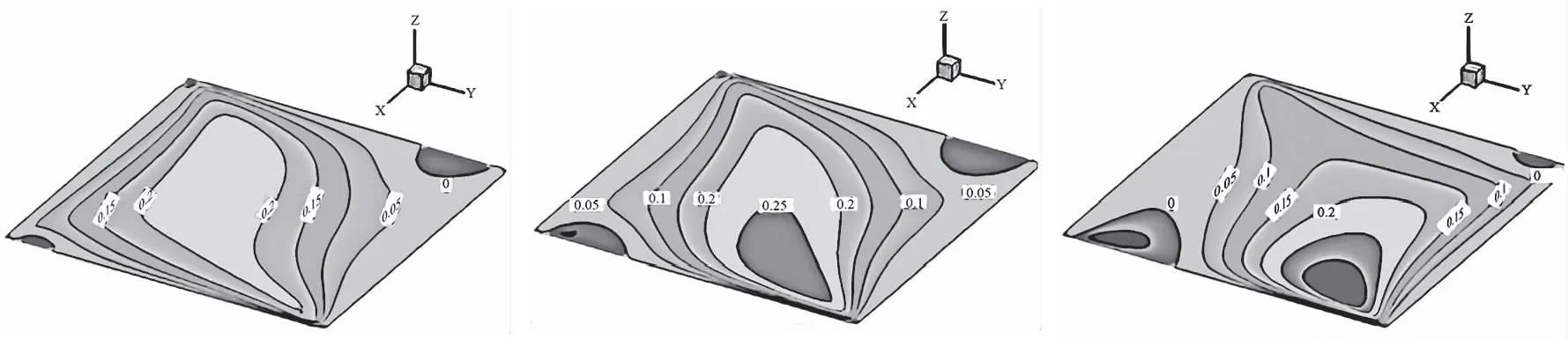
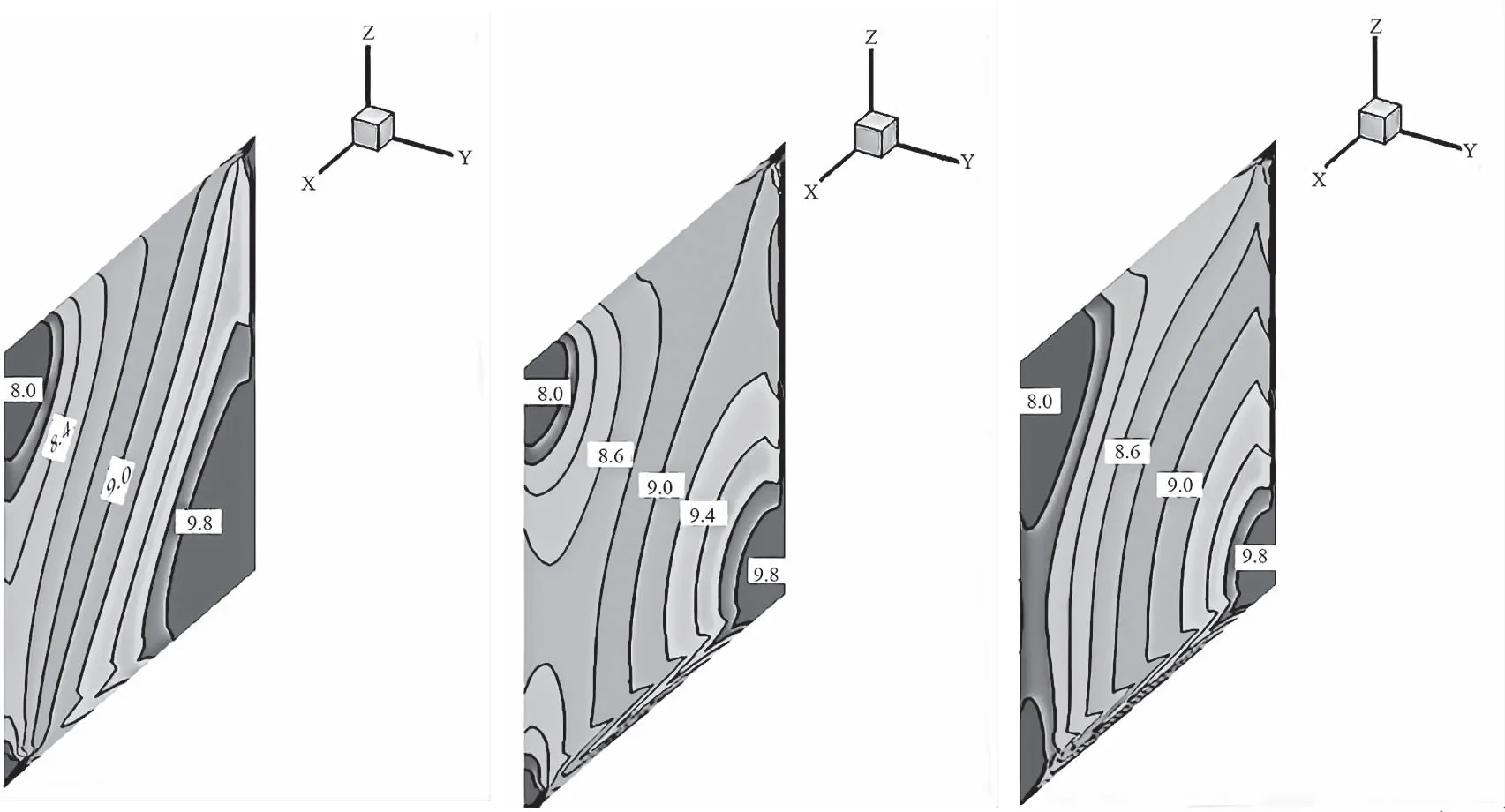
图3—图6为Re=10，网格划分50×50×50时流场中x,y,z方向的速度等值线图及纵向各截面的压强等值线图。

由图3—图5可以看出，槽道中x方向的流动速度较大，所以x方向的速度分布在横向各截面上都呈现对称分布，中部速度为最大值约等于1.0，槽道壁面上速度为零，满足边界无滑移条件；槽道中y,z方向的流动速度较小，从图4可以发现槽道下游右侧y方向的速度较大，由图5中可看出，z方向的速度变化是上游右侧的速度大于下游右侧的速度，随着深度的变化，上游右侧的速度变为小于下游右侧的速度；整体上通过观察比较图4和图5可以发现，离入口截面越远的x方向下游y,z方向的速度较大，能清晰明显的看出流场的三维效应。图6为纵向各截面压强等直线图，从图中可看出，上游下部到下游上部压强值从大到小呈梯度变化，在y方向上越往下游，这种压强的梯度变化越明显，压强值的这种变化规律主要是由于流体速度的变化的影响，因为从图4和图5中可看出在流场中下游右侧的三维效应比较明显，速度变化率大，压强较小，符合三维槽道流场的真实物理变化规律。

(a)z=0.2 (b)z=0.5 (c)z=0.8

(a)z=0.2 (b)z=0.5 (c)z=0.8

(a)z=0.2 (b)z=0.5 (c)z=0.8

(a)y=0.2 (b)y=0.2 (c)y=0.2

3 结论

利用程序设计语言VC++编写三维投影法的数值计算程序，并对具有精确解的三维Poisson方程和三维纯流体的槽道进行数值模拟计算，结论如下：

1)迭代法比较容易实现，三维数值问题求解的大型方程组维数远超出二维情况，直接数值求解和计算机存储变得更加困难，据此结合迭代法原理将三维问题化为二维问题，利用二维问题大型稀疏线性方程组的快速求解和数据结构优化存储方法，既能减小存储空间，又能实现快速准确求解三维复杂流场问题，且由迭代法引起的计算误差也非常小，求解保持了良好的数值稳定性。

2)对压力Poisson方程进行数值模拟，验证了数值算法的网格依赖性和迭代误差的可控性，通过比较计算结果与解析解，验证了该数值算法的有效性和可靠性。

3)以纯流体的三维槽道流场为基准数值算例，得到的计算结果与真实的物理规律现象基本相符，验证了基于投影法的三维流场数值求解结果的可行性。