基于功率比的混合动力汽车模糊自适应等效燃油消耗最小策略研究

施德华,容香伟,汪少华,3,陈龙

(1.江苏大学汽车工程研究院,212013,江苏镇江;2.重庆理工大学汽车零部件先进制造技术教育部重点实验室,400054,重庆;3.江苏省新能源汽车电驱动系统与智能控制工程研究中心,212013,江苏镇江)

作为汽车节能技术之首,混合动力技术得到了国内外企业和高校的深入研究[1]。2020年发布的《节能与新能源汽车技术路线图2.0》明确提出要大力发展混合动力技术。其中,以行星排和双电机驱动为核心的功率分流式系统得到了国内外整车企业和研究机构的浓厚兴趣[2-3]。针对混合动力系统的多动力源协同工作,能量管理策略优化对于发挥系统燃油经济性具有重要意义[4]。

基于规则的控制策略实现简单,但基于特定工况标定或寻优获得的逻辑门限参数无法保证混合动力汽车(HEV)大范围工况下高效工作。基于动态规划的全局优化策略能够求取全局最优值,但依赖于对工况的预先获取,计算量大,不利于实时在线应用[5]。等效燃油消耗最小策略(ECMS)通过等效因子将电池电量消耗等价为燃油消耗,通过实时寻优确定使总等效消耗最小的控制[6]。基于固定等效因子的ECMS工况适应性差,无法满足不同车速特征的车辆经济性控制需求[7]。为实现复杂工况下的电池充放电平衡,国内外学者提出了等效因子自适应优化机制。Enang等提出了基于SOC反馈的等效因子比例或比例-积分调节机制,通过对电池SOC的约束使电池实际值跟踪参考值,从而实现充放电平衡[7-9]。然而,仅基于电池SOC平衡的等效因子反馈调节对于复杂工况下整车燃油经济性的改善仍存在一定局限性。随着大数据、智能交通(ITS)和预测技术的快速发展,未来路段内的车速、能量等特征信息可以被用来实现等效因子的前馈调节。车速、转矩或功率(能量)等预测信息可以基于指数函数、马尔科夫、神经网络等方法获得[10]。Kazemi等在基于电池SOC状态反馈的PI控制器基础上,进一步提出了基于预测工况的3种不同等效因子自适应修正模型[11]。张风奇等提出了基于预测车速的等效因子在线修正方法[12-13]。

纵观国内外研究现状可以看出,大多数文献通过建立等效因子与工况特征信息相关的显式表达获取等效因子的自适应修正方法,但HEV工况特征和能量管理策略对整车能耗的影响特征复杂,难以精确建立等效因子显示表达模型。模糊控制将复杂系统的控制问题描述为一种基于语言的分析模型,不依赖于精确的数学模型,具有较强的鲁棒性和容错能力[14-15]。Zhao等针对HEV燃油经济性、电池SOC以及控制量之间的复杂非显示关系,提出了基于专家经验知识的代价因子模糊调节机制[16]。付主木等提出了一种基于模糊控制的ECMS,以提升ECMS的工况适应性[17]。但是,Zhao和付主木等主要基于车辆行驶中产生的电能模糊修正等效因子,没有考虑未来路段工况信息的影响。工况的准确描述依赖于特征参数的选取与组合,如平均车速、怠速时间、最大加速度、最大速度等,特征参数的增多将显著增加等效因子的自适应求解难度[18]。

由于路段平均功率直接反映了车辆的能量需求,本文以相邻时段平均功率作为ECMS等效因子前馈调节变量,提出基于历史平均功率和预测平均功率信息的混合动力汽车自适应ECMS策略。建立基于比例修正的ECMS等效因子显示自适应求解模型,通过研究电池SOC实际值、参考值以及未来时段与历史时段的平均功率对等效因子调节的影响行为,提出基于多模糊控制器自适应切换的比例因子修正方法,以解决基于固定比例自适应求解等效因子的不足,为基于ECMS的能量优化管理提供一种新的思路。

1 混合动力系统建模

1.1 混合动力构型

研究的功率分流式HEV结构如图1所示。发动机与行星排PG1的行星架连接,电机MG1连接到PG1的太阳轮,电机MG2连接到行星排PG2的太阳轮,PG2的齿圈固定,系统输出轴与主减速器连接,发动机和两个电机的耦合动力经过PG1的齿圈和PG2的行星架传递到输出轴,并驱动车辆行驶。系统关键部件参数如表1所示,相关参数参考丰田Prius混合动力车型。

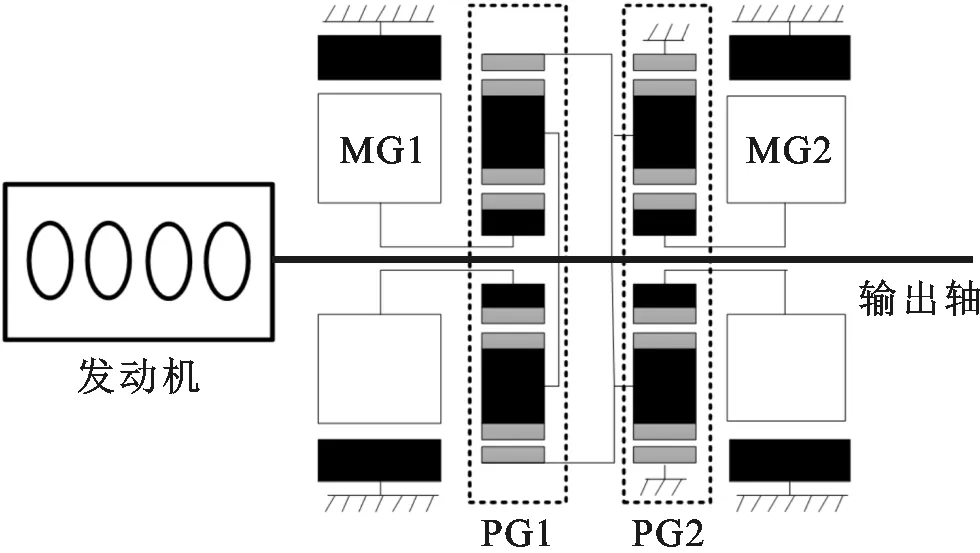
图1 混合动力构型Fig.1 Configuration of the powertrain

表1 混合动力汽车参数Table 1 Specifications of the HEV

1.2 混合动力系统建模

基于杠杆理论及车辆纵向动力学模型建立混合动力系统的燃油经济性评估模型[19]。准稳态工况下系统转速转矩耦合关系为

(1)

(2)

式中:ωE和TE分别为发动机转速和转矩;ωG和TG分别为MG1的转速和转矩;ωM和TM为MG2的转速和转矩;ωout和Tout表示输出轴的转速和负载转矩;K1和K2分别为PG1和PG2中齿圈与太阳轮的齿数比。忽略道路坡度,负载转矩为

(3)

式中:Tbrk车辆制动时的摩擦力矩;id为主减速比;v为车速;ρair、Af、Cd和g分别为空气密度、迎风面积、空气阻力系数和重力加速度。

基于等效内阻模型描述电池的动力学行为,电池荷电状态(SOC)fSOC表示为

(4)

(5)

式中:Voc和Rb分别为电池开路电压和电池内阻;Ibat为电池电流;Qb为电池容量;PL为负载功率,受MG1和MG2工作状态的影响,表示为

(6)

其中ηG和ηM分别为电机MG1和MG2的效率,γ=1,-1分别表示电机处于发电和耗电状态。

2 自适应等效燃油消耗最小策略

ECMS引入等效因子将电池电能消耗等效为相应油耗,通过实时优化包含发动机油耗和等效燃油消耗的目标函数求解最优控制,目标函数为[2,9]

(7)

(8)

λ=(1+sgnPL)/2

(9)

(10)

其中Rdis和Rchg分别表示电池放电和充电过程的内阻。

受到电池、发动机和电机等物理特性的约束,系统优化求解的约束条件为

(11)

为实现不同工况下的电池充放电平衡,Onori等提出以固定的时间间隔根据反馈电池SOC调节等效因子,其基本原理如图2所示[8]。即:前一时段(k-1～k)的等效因子Seqact_A(k-1)如果远低于能够维持该时间段电池充放电平衡的最优等效因子Seq_opt(k-1),电池具有放电趋势,若不调整,在下一时间段(k～k+1)电池仍将继续放电,甚至导致过放,此时需增大等效因子,如使其为Seqcorr_A(k),以减小电池放电甚至使电池具有充电趋势;反之,若前一时间段(k-1～k)的等效因子Seqact_B(k-1)远高于能够维持该时间段电池充放电平衡的最优等效因子Seq_opt(k-1),电池具有充电趋势,若不调整,在下一时间段(k～k+1)电池仍将继续充电,需要减小等效因子,如修正为Seqcorr_B(k),以减小电池充电甚至使电池具有放电趋势。据此,Onori等将等效因子自适应策略描述为

Seq(k)=Seq(k-1)+Kp(fSOCref-fSOC(k))

(12)

图2 等效因子自适应原理[8]Fig.2 Adaptive principle of the equivalence factor

式中:Seq(k-1)和Seq(k)分别表示前一时段和当前时段内的等效因子;fSOCref为电池参考SOC;fSOC(k)为第k时间段初始时刻的电池SOC真实值;Kp为SOC参考值与真实值偏差的比例增益。

3 ECMS模糊自适应策略

3.1 模糊自适应ECMS控制原理

虽然由式(12)表示的方法通过对等效因子的阶段性修正能够更好地维持不同工况下的电池充放电平衡,但由图2可以看出,不同等效因子下对电池充放电平衡特性的分析忽略了不同时段整车功率需求和电池实际SOC值的影响。事实上,即便在前一时间段选定的等效因子远低于能够维持电池充放电平衡的最优等效因子,使得电池具有放电趋势,但若电池实际SOC在下一时间段开始时仍高于参考值,则仍可以选定较小等效因子,使电池继续放电,避免电池具有充电趋势,而非必须增大等效因子;同理,若整车需求功率在下一阶段较小,如拥堵路况,也可以使等效因子继续保持较小的值,从而使HEV在下一时间段由电机更多地参与驱动。

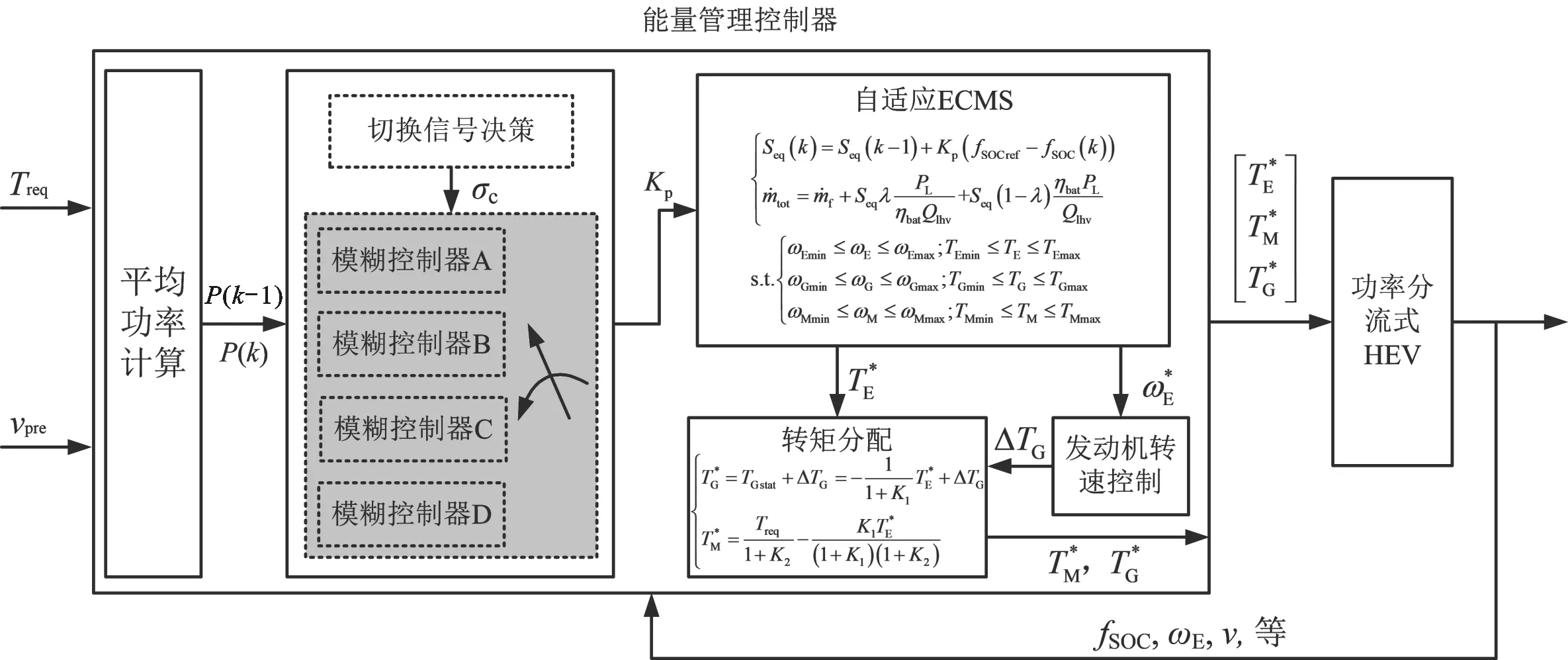
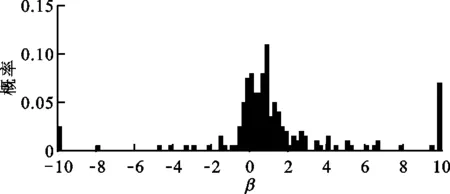
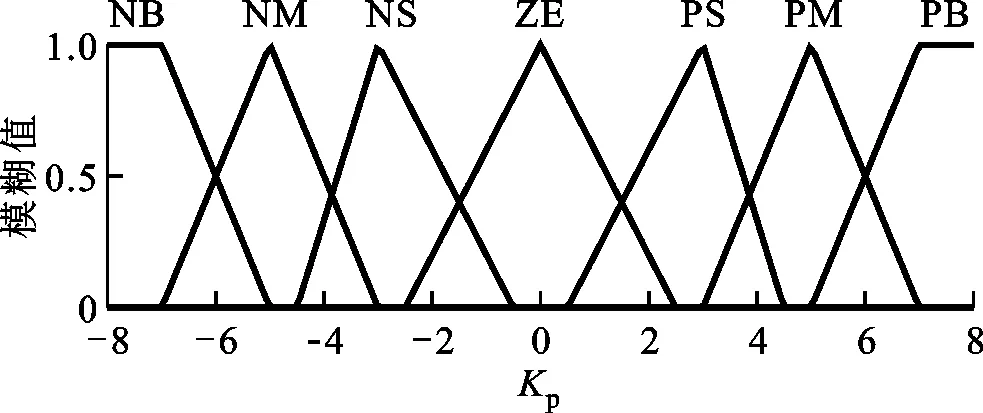
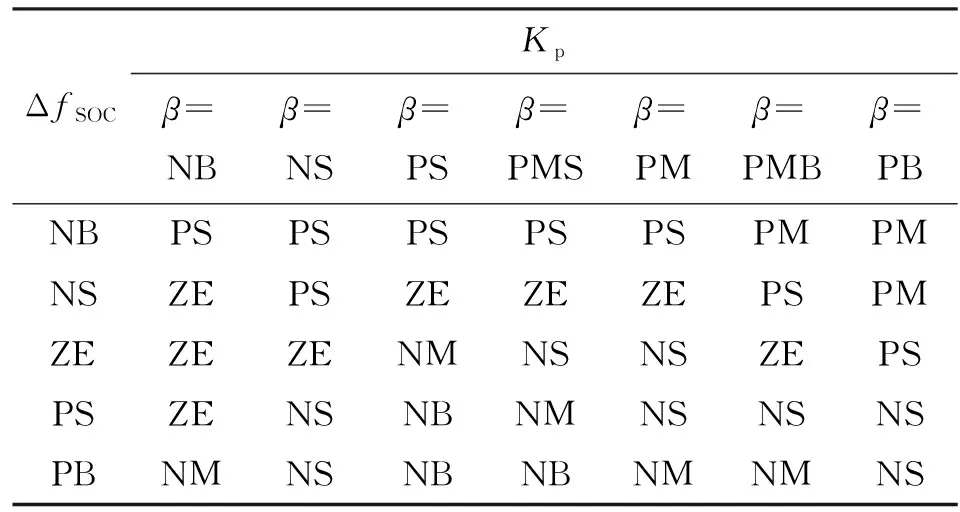
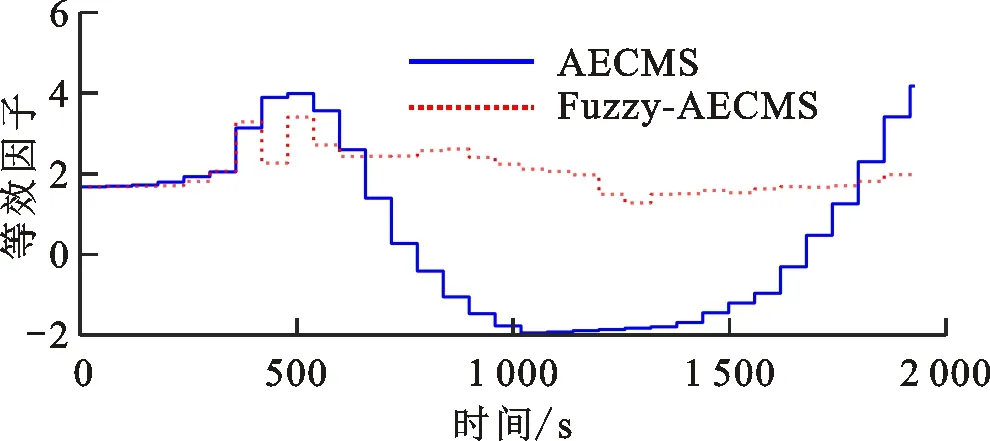
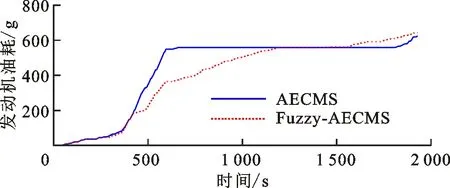
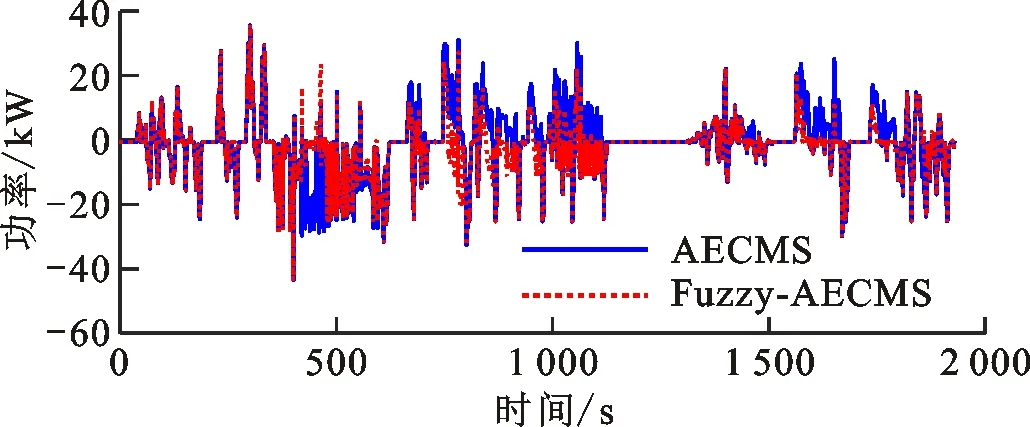
因此,单纯基于当前实际SOC与参考值的偏差修正等效因子作为一种事后补偿机制势必存在一定的局限性,有必要综合考虑前一时段以及当前时段平均需求功率P(k-1)和P(k)、前一时段电池荷电状态变化ΔfSOC,以及fSOC(k)与参考值fSOCref之间的关系等不同因素对等效因子修正机制的影响行为。如当fSOC(k)P(k-1)且fSOC(k)远低于fSOCref,需要增大等效因子以减小放电趋势,而当fSOC(k)略低于fSOCref时,可以适当增大等效因子,使电池有充电趋势或适当放电;当P(k)

基于上述分析,需要针对P(k-1)、P(k)、ΔfSOC、fSOC(k)和fSOCref之间的关系选取合适的比例增益Kp,但不同变量间的关系对Kp的影响特性复杂,难以用准确的数学模型定量描述。模糊控制基于模糊集合、模糊语言变量和模糊逻辑推理建立输入与输出的智能映射关系,对于解决难以精确描述的数学模型控制问题具有突出优势[14-15]。

图3 基于模糊自适应ECMS的能量管理原理Fig.3 Energy management principle based on fuzzy adaptive ECMS

3.2 控制策略设计

切换信号决策模块根据P(k-1)以及fSOC(k)和fSOCref的关系确定模糊控制器切换信号,定义

(13)

(14)

则切换信号描述为

σc=MSOC+2MP+1

(15)

切换信号σc=i(i=1,2,3,4)分别对应“模糊控制器A～D”。各模糊子控制器的输入为前一时段的电池SOC变化ΔfSOC和反映相邻时段工况信息关系的功率比β,分别表示为

fSOC=fSOCfin(k-1)-fSOCini(k-1)

(16)

(17)

式中:fSOCini(k-1)和fSOCfin(k-1)分别表示前一时段电池SOC的初始值和最终值。

P(k)与P(k-1)由平均功率计算模块根据车速信息基于车辆动力学平衡方程求得,表示为

(18)

式中:tini,k、tend,k分别为第k阶段的初始时刻和最终时刻;Fr、Fg、Fair和Fa分别表示滚动阻力、坡度阻力、空气阻力和加速阻力。

(19)

式中MG1动态补偿转矩ΔTG由发动机转速控制模块根据理想与实际转速差基于PI控制求解。

为了确定输入变量的论域,基于标准循环工况分析,选定工况包括INDIA_HWY_SAMPLE、INDIA_URBAN_SAMPLE、WLTC、NEDC、UDDS、HWFET、CSHVR_Vehicle和UNIF01,相关工况从ADVISOR2002中导出[10,20]。以60 s间隔划分工况,求取不同工况片段平均功率,并获取相邻片段的功率比,其分布如图4所示。总体而言,功率比主要为正值,且集中分布在0～6的区间内。选定平均功率比的论域为[-10,10],比例增益为1。由于车辆大多数工况处于驱动状态,对于模糊控制器A和B,当P(k-1)<0时,功率比语言变量为{NB,NS,PS,PB};当P(k-1)>0时,模糊控制器C和D中功率比语言变量定义为{NB,NS,PS,PMS,PM,PMB,PB}。其中,NB、NS、PS、PMS、PM、PMB和PB分别表示负大、负小、正小、正中小、正中、正中大和正大。不同模糊控制器的功率比隶属度函数如图5所示。

图4 功率比概率分布Fig.4 Probability distribution of the power ratio

(a)模糊控制器A和B

(b)模糊控制器C和D图5 不同模糊控制器的功率比隶属度函数Fig.5 Membership function of the power ratio for different fuzzy controllers

基于选定工况,采用动态规划(DP)获取各工况下的全局最优值,通过分析各划分片段内电池SOC偏差确定ΔfSOC的论域和隶属度函数。DP基于贝尔曼最优原理进行多阶段决策,将时间序列按ΔT的步长离散为不同阶段,并采用逆向递推的方式获取最优解

(20)

第k阶段在状态变量x(k)和控制变量u(k)作用下,系统代价函数定义为

(21)

为了实现严格的电池充放电平衡,设定fSOC(N)=fSOC(1),物理约束条件与式(11)相同。状态变量为SOC,控制变量为发动机转矩和转速,状态和控制变量均离散化。DP求解过程为

(22)

(23)

图6 ΔfSOC概率分布Fig.6 Probability distribution of ΔfSOC

图7 ΔfSOC隶属度函数Fig.7 Membership function of ΔfSOC

各模糊控制器输出量的语言变量定义为{NB,NM,NS,ZE,PS,PM,PB},分别表示负大、负中、负小、零、正小,正中和正大,论域为[-8,8],比例增益为1,其隶属度函数如图8所示。各模糊控制器的模糊规则如表2～5所示。

图8 比例增益隶属度函数Fig.8 Membership function of the proportional gain

表2 模糊规则表(模糊控制器A)Table 2 Fuzzy rule (fuzzy controller A)

表3 模糊规则表(模糊控制器B)Table 3 Fuzzy rule (fuzzy controller B)

表4 模糊规则表(模糊控制器C)Table 4 Fuzzy rule (fuzzy controller C)

表5 模糊规则表(模糊控制器D)Table 5 Fuzzy rule (fuzzy controller D)

4 仿真分析

为验证所提出的基于功率比的模糊自适应等效燃油消耗最小策略的有效性,以前述8种工况作为测试工况,对采用由式(12)所示的控制策略和本文所设计的模糊策略(分别记为AECMS和Fuzzy-AECMS)进行对比分析。设定电池SOC参考值和初始值为0.55,等效因子自适应修正周期为60 s,综合各测试工况,选取AECMS中等效因子初始值和比例增益分别为1.68和4.3。

图9给出了UNIF01工况下采用不同控制策略时的仿真结果,包括车速跟踪效果、等效因子、电池SOC、发动机油耗、发动机转矩转速以及各电机的输出功率。由图可知,两种策略下车辆实际车速均能很好地跟随参考车速。由图9b可以看出,在660～1 800 s的工况区间内,相较于本文提出的Fuzzy-AECMS策略,由式(12)所示的等效因子自适应修正策略使等效因子更小,甚至为负值(800～1 680 s工况区间),导致电池电能消耗评估权重降低,即由电池电能等效的燃油消耗更“廉价”,因此车辆更倾向于由电机驱动,工作在纯电动模式,发动机参与度显著降低,如图9e和9f所示。发动机油耗在660～1 800 s的工况区间内也几乎为0,电池整体表现为放电趋势,如图9d和9c所示。相比之下,本文所设计的Fuzzy-AECMS根据前后工况片段的功率比以及当前电池SOC对等效因子能够较为准确地评估,在660～1 800 s的工况区间内通过对等效因子的自适应调节有效地维持了电池充放电平衡。AECMS和Fuzzy-AECMS策略下电池最终SOC分别为0.380和0.532,AECMS使得电池最终SOC相较初始值0.55显著降低,电池放电明显,因而发动机油耗也略低,而Fuzzy-AECMS更好地维持了电池的充放电平衡。由发动机和电机的响应结果可以看出,由于对发动机、MG1和MG2输出转速和转矩的限制,不同动力源的输出量均在额定范围内,满足车辆控制要求。

(a)工况车速

(b)等效因子

(c)电池SOC

(d)发动机油耗

(e)发动机转矩

(f)发动机转速

(g)MG1功率

(h)MG2功率图9 UNIF01工况下仿真结果对比Fig.9 Simulation results comparison under UNIF01 condition

不同工况下电池最终SOC相较初始值变化、发动机燃油消耗(EFC)和整车等效燃油经济性(EFE)如图10所示[21]。图10b中,AECMS策略下的EFC和EFE分别记为AECMS-EFC和AECMS-EFE,相应地,有Fuzzy-AECMS-EFC和Fuzzy-AECMS-EFE。由图10可知,NEDC工况下,两种策略均使电池充放电平衡得到了很好的控制,且EFC和EFE也相近。CSHVR_Vehicle工况下,虽然AECMS实现了更好的电池充放电平衡,但Fuzzy-AECMS使SOC最终值相较初始值仅增加2.18%,也实现了优越的电池充放电平衡,同时使得最终SOC增加的情况下具有更低的发动机油耗,因而具有更优越的整车等效燃油经济性,相较于AECMS策略,EFE提高了6.01%。在其他测试工况下,本文提出的Fuzzy-AECMS使电池SOC最终值更好地维持在参考值0.55附近,实现了更优越的电池充放电平衡,尤其是在UNIF01和INDIA_HWY_SAMPLE工况下,AECMS使得电池的放电和充电趋势明显。虽然在WLTC、UDDS、HWFET和UNIF01下,Fuzzy-AECMS使得发动机油耗EFC有所增加,但这源于更高的电池SOC最终值。总体而言,Fuzzy-AECMS使整车具有更优越的等效燃油经济性和电池充放电平衡维持特性,不同工况下整车等效燃油经济性改善程度如表6所示。

(a)电池SOC变化

(b)发动机油耗和等效燃油经济性图10 不同工况不同策略仿真结果对比Fig.10 Simulation results of different strategies in different cycles

表6 不同工况下等效燃油经济性改善程度Table 6 Improvement of EFE in different cycles

5 结 语

(1)针对仅采用实时反馈电池SOC比例修正等效因子的不足,提出了基于多模糊控制器切换的等效因子自适应求解方法,确定了多模糊控制器切换机制,定性分析了不同因素对等效因子修正需求的影响行为,为模糊自适应规则的制定提供依据。

(2)基于常用标准循环工况求取了不同工况片段内的平均功率以及相邻工况片段的功率比,采用动态规划算法获取了选定标准循环工况的全局最优解,通过研究功率比和不同时段全局最优SOC偏差的分布特性,确定了多模糊控制器的控制参数。

(3)相较于仅采用实时反馈电池SOC进行等效因子比例修正的AECMS,虽然本研究提出的PR-AECMS在NEDC和INDIA_HWY_SAMPLE工况下使整车等效燃油经济性分别降低了0.32%和1.85%,但在WLTC、INDIA_URBAN_SAMPLE、CSHVR_Vehicle和UNIF01工况下等效燃油经济性分别提高了3.20%、4.51%、6.01%和12.09%,同时实现了更优的电池充放电平衡,能够满足大范围工况下混合动力汽车整车能量的高效管理需求。