角平分线模型及应用
2022-02-14陈诗玉邹兴平
陈诗玉 邹兴平

[构建模型]
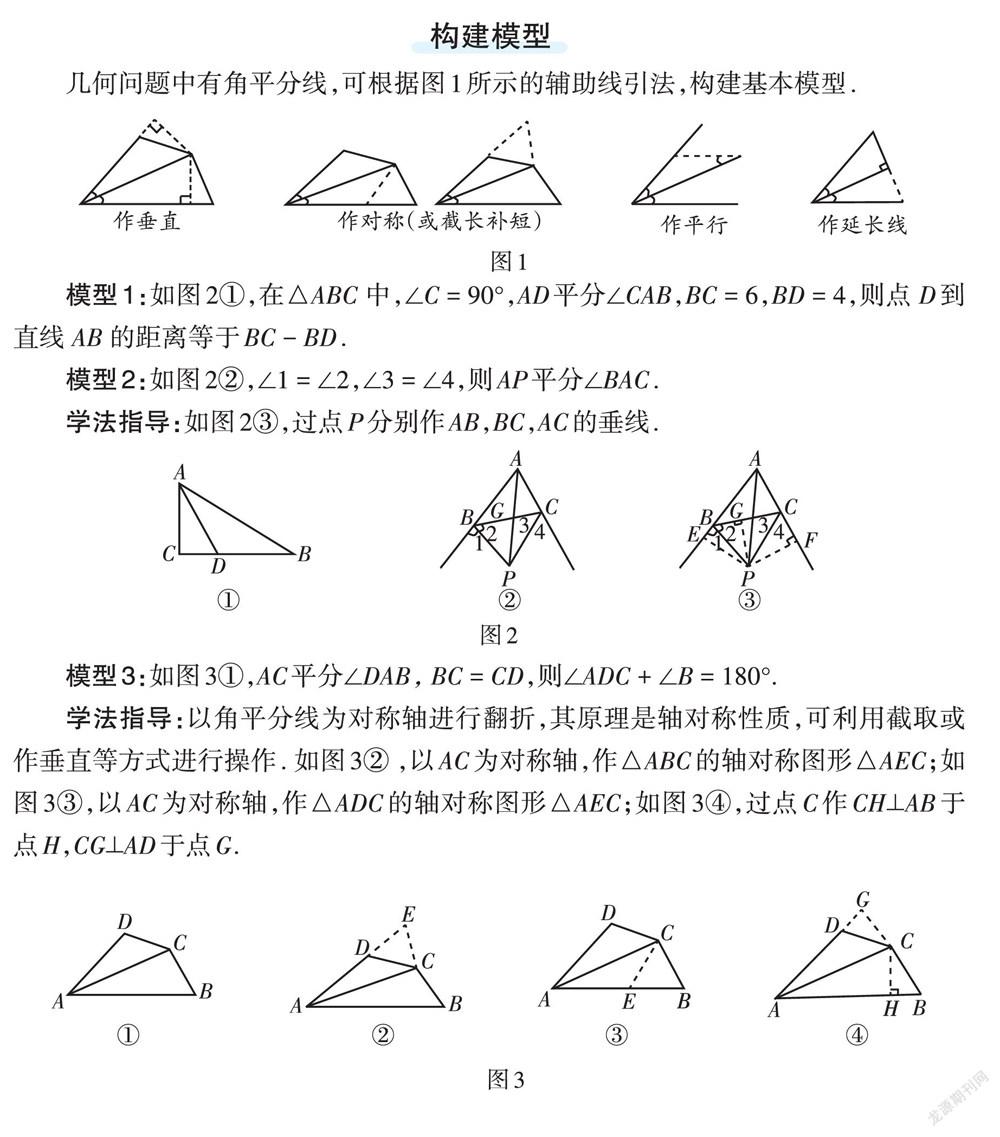
几何问题中有角平分线,可根据图1所示的辅助线引法,构建基本模型.
模型1:如图2①,在△ABC 中,∠C = 90°,AD平分∠CAB,BC = 6,BD = 4,则点 D到直线 AB 的距离等于BC - BD.
模型2:如图2②,∠1 = ∠2,∠3 = ∠4,则AP平分∠BAC.
学法指导:如图2③,过点P分别作AB,BC,AC的垂线.
模型3:如图3①,AC平分∠DAB, BC = CD,则∠ADC + ∠B = 180°.
学法指导:以角平分线为对称轴进行翻折,其原理是轴对称性质,可利用截取或作垂直等方式进行操作. 如图3② ,以AC为对称轴,作△ABC的轴对称图形△AEC;如图3③,以AC为对称轴,作△ADC的轴对称图形△AEC;如图3④,过点C作CH⊥AB于点H,CG⊥AD于点G.
模型4:如图4,P 是∠MON的平分线上一点,过 P 作 PQ[⫽]ON,交 OM 于点Q,则△POQ 是等腰三角形.
模型5:如图5,P 是∠MON 的平分线上一点,AP⊥OP,A在OM上,延长AP交ON于点 B,则△AOB 是等腰三角形.
1.(1)如图6①,AD是△ABC 的外角平分线,P是AD上异于点A 的任意点,比较 PB + PC 与 AB + AC 的大小,并说明理由;(2)如图6②, AD 是△ABC 的角平分线,其他条件不变,比较PC - PB 与 AC - AB 的大小,并说明理由.
学法指导:(1)联想模型3,如图6③,在BA的延长线上取一点E,使AE = AC,连接EP,得 PB + PC > AB + AC;(2)联想模型3,如图6④,在AC上取一点E,使AE = AB,连接EP,得 PC - PB < AC - AB.
2.如图7,已知等腰直角三角形 ABC中,∠A = 90°,AB = AC,BD 平分∠ABC,CE⊥BD,垂足为 E. 求证:BD = 2CE.
學法指导:联想模型3,延长BA,CE交于点F.
3.(1)如图8①,△ABC 中,EF[⫽]BC,D 在 EF 上,BD,CD 分别平分∠ABC,∠ACB,写出 EF 与 BE,CF 的数量关系;(2)如图8②,BD 平分∠ABC,CD 平分∠ACG,DE[⫽]BC,交 AB 于 E,交 AC于 F,写出 EF 与 BE,CF 的数量关系;(3)如图8③,BD,CD分别为∠CBM,∠BCN 的平分线, 过点D作BC的平行线,交AB的延长线于E,交 AC的延长线于F,写出 EF与 BE,CF 的数量关系.
学法指导:联想模型4,得出结论:(1)EF = BE + CF;(2)EF = BE - CF;(3)EF = BE + CF.
