折叠问题的解题策略

何婷

本课选自辽宁教育学院“学到汇”公众服务平台“辽宁省初中数学学科教研核心团队名师公益学堂”，旨在引领教师专业发展，服务学生自主学习，减轻学生学业负担。

折叠问题通常以三角形或四边形为原始图形，折叠的过程是作轴对称变换的过程，其隐藏条件较多，如：折叠过程一定会产生全等图形，有线段相等、角相等、面积相等的结论;折痕具有双重身份——其所在直线是对称轴（即对应点连线的中垂线，通常是引辅助线的依据），折痕所在的射线是角平分线.

折叠问题的破解策略：首先要抓住折痕，找全折叠隐含的条件，再识别基本模型，运用模型转化边角关系，最后结合数据直接或列方程求解.

模型构建

一、轴对称全等模型

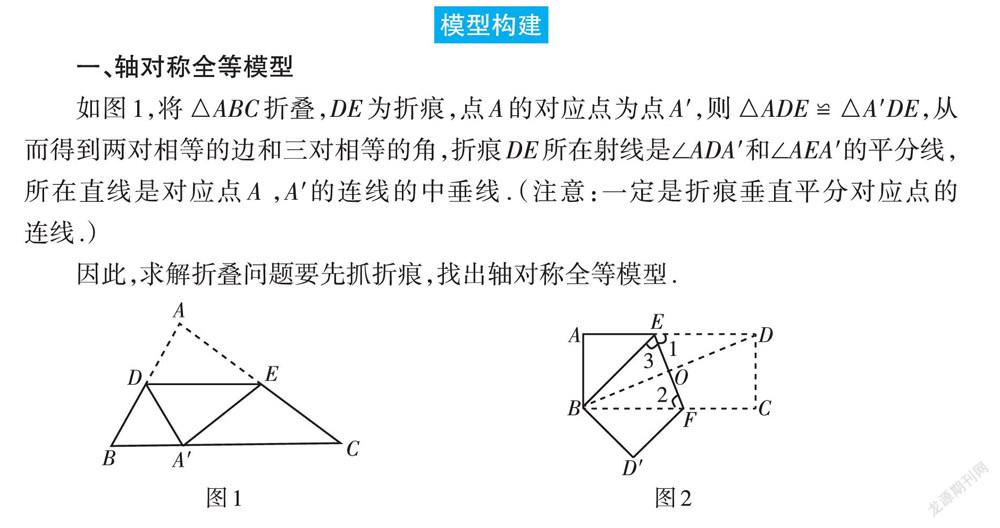
如图1，将[△A]BC折叠，[DE]为折痕，点A的对应点为点A'，则[△A]DE ≌ [△A']DE，从而得到两对相等的边和三对相等的角，折痕[DE]所在射线是∠ADA'和∠AEA'的平分线，所在直线是对应点A ，A'的连线的中垂线.（注意：一定是折痕垂直平分对应点的连线.）

因此，求解折叠问题要先抓折痕，找出轴对称全等模型.

二、8字型全等模型与平行中点8字型全等模型

如图3，AD[⫽]BC，AB[⫽]DC，折叠四边形[ABC]D，[BD]为折痕，点C的对应点为点C'，由轴对称模型有[△]CBD ≌ [△C']BD，得到相等的边和角，易得[△]AOB ≌ [△C']OD，可得一对8字型全等模型. 若条件中再有平行或中点，则可考虑平行中点8字型全等模型.

在图2中，折叠矩形ABCD，EF为折痕，点D对应点B，点C对应点D'，则[EF]垂直平分BD，易得平行中点8字型全等模型[，即△DOE≌△BOF].

三、铁三角模型

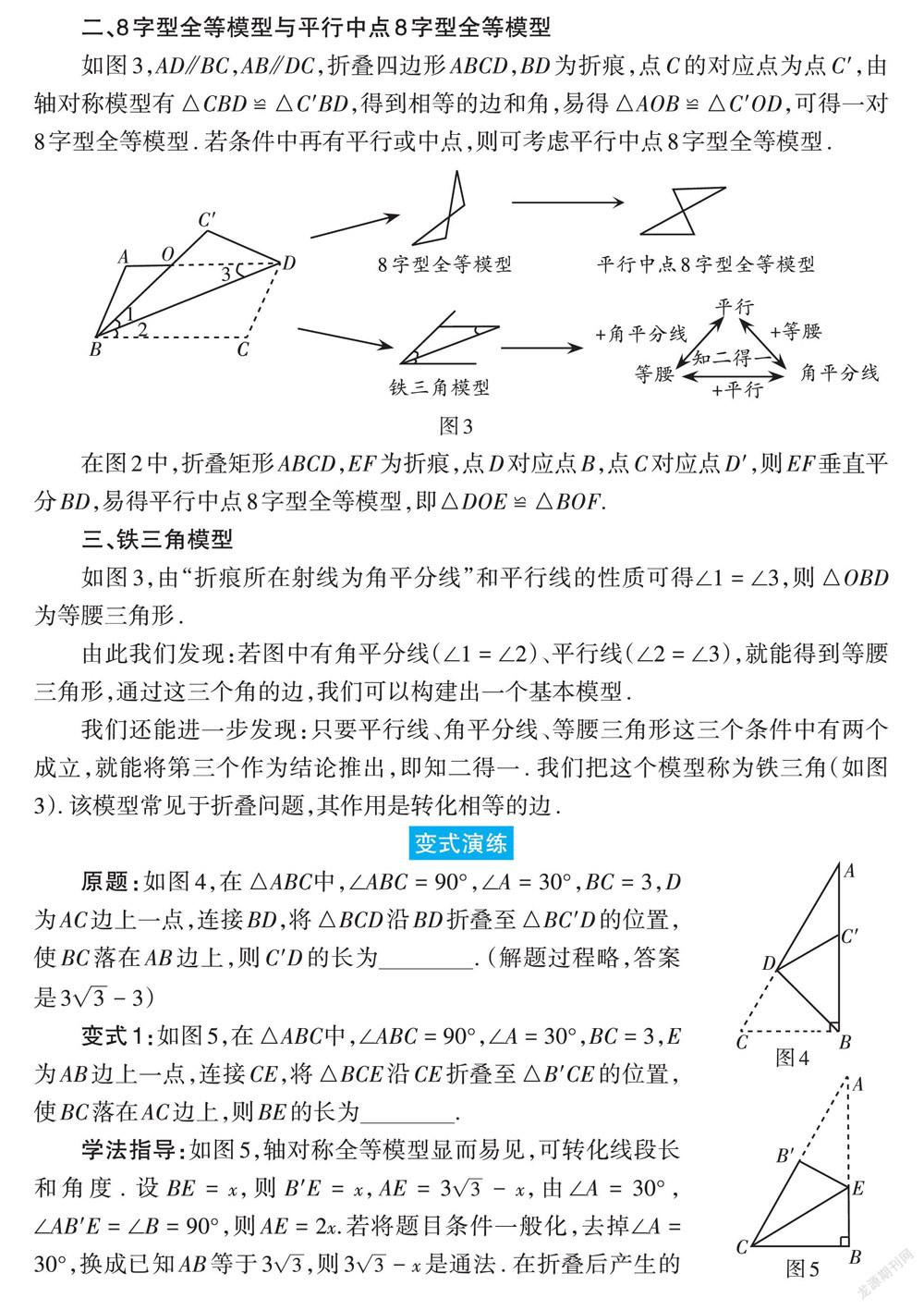
如图3，由“折痕所在射线为角平分线”和平行线的性质可得∠1 = ∠3，则[△OBD]为等腰三角形.

由此我们发现：若图中有角平分线（∠1 = ∠2）、平行线（∠2 = ∠3），就能得到等腰三角形，通过这三个角的边，我们可以构建出一个基本模型.

我们还能进一步发现：只要平行线、角平分线、等腰三角形这三个条件中有两个成立，就能将第三个作为结论推出，即知二得一. 我们把这个模型称为铁三角（如图3）. 该模型常见于折叠问题，其作用是转化相等的边.

变式演练

原题：如图4，在[△ABC中]，∠ABC = 90°，∠A = 30°，BC = 3，D为AC边上一点，连接BD，将[△]BCD沿BD折叠至[△]BC'D的位置，使BC落在AB边上，则C'D的长为___________. （解题过程略，答案是3[3] - 3）

变式1：如图5，在[△ABC中]，∠ABC = 90°，∠A = 30°，BC = 3，E为AB边上一点，连接CE，将[△]BCE沿CE折叠至[△]B'CE的位置，使BC落在AC边上，则BE的长为___________.

学法指导：如图5，轴对称全等模型显而易见，可转化线段长和角度. 设BE = [x]，则B'E = [x]，AE = 3[3] - [x]，由∠A = 30°，∠AB'E = ∠B = 90°，则AE = 2[x].若将题目条件一般化，去掉∠A = 30°，换成已知AB等于3[3]，则3[3] - [x]是通法. 在折叠后产生的Rt[△A]B'E中，利用勾股定理列方程求得[x] = [3]，即BE = [3].

变式2：如图6，在[△ABC中]，∠ABC = 90°，∠A = 30°，BC = 3，E为BC边的中点，D为AB边上一点，连接DE，将[△]BDE沿DE折叠至[△]B'DE的位置，B恰好落在AC边上，求BB'和DE.

学法指导：此题为轴对称模型加中点的综合应用.由轴对称模型知BE = B'E，DE垂直平分B'B，结合E为BC的中点，得BE = B'E = CE（此为我们熟悉的双等腰模型），可得∠CB'B = 90°，BB'既可用含30°角的直角三角形的性质，也可用等积法求解. 易得DE[⫽]AC，则∠EDB = ∠A = 30°，从而DE = 2BE = 3.

变式3：如图7，在[△ABC中]，∠ABC = 90°，∠A = 30°，BC = 3，D为AC边的中点，连接BD，将[△A]BD沿BD折叠至[△A']BD的位置，[A']B交AC于点E，连接[A']C，求A'C的长.

学法指导：识别轴对称模型，可知∠2 = ∠3，∠A = ∠4 = 30°，[AD] = [A']D，又由D为AC的中点，可知[CD] = [A]D，[CD] = [BC]，则[A']D = [BC]，易看出[△]DCB为等边三角形，则∠1 = ∠2 = ∠3 = 30°，即∠4 = ∠1 = 30°，则[A']D[⫽]BC，易证[得A']C = BD = 3.

变式4：在矩形ABCD中，AB = 5，BC = 12，按如图8的方式折叠，使点B与点F重合，AC为折痕，则AE = .

学法指导：图8中有[△A]BC与[△A]FC全等组成的轴对称模型，有[△A]FE与[△]CDE组成的8字型全等模型，有角平分线加平行线组成的铁三角模型，那么哪个模型对求解这道题有帮助呢？显然，与待求线段AE相关的是鐵三角模型和8字型全等模型，其中铁三角模型不需证明全等，转化边更方便，因此设[CE] = [A]E = [x]，DE = 12 - [x]，则在Rt[△]DEC中可求得[x] = [16924]，故应填[16924].

如图9，∠ABC = 40°，点E是射线BC上一动点，把△ABE沿AE折叠，点B的对应点为点D，当直线AD⊥BC时，∠ABC等于 .（答案见第33页）