正交车铣杆类胚料切削力的研究

2022-02-13孙晋亮杨永琳谭志银

滁州职业技术学院学报 2022年4期

孙晋亮，杨永琳，谭志银

(滁州职业技术学院电气工程学院，安徽滁州 239000)

由于选取不同齿数的铣刀车铣胚料时，同时参与切削的铣刀齿数是不同的，因此正交车铣加工杆类胚料的切削过程切削力是不断变化的。所以对此过程的分析与传统的车削分析相比还是非常困难的[1-2]。但是正交车铣加工杆类零件的加工表面质量和加工精度与切削力的变化息息相关，因此对正交车铣切削杆类胚料的切削力分析和研究十分有必要。

一、瞬间切削齿数的模型建立

为了便于推理，假设所选铣刀的每个刀齿在几何形状上完全相同，均匀分布在铣刀的圆周上，且每个刀齿的刀尖都位于同一圆周上，因而在切削加工时产生的切削震动位移相等。建立图1a所示的正交车铣加工杆类胚料外圆的切削模型，图1b所示为正交车铣加工杆类胚料的铣刀切削加工时的局部放大图。为了方便分析在铣刀的外圆周上设立B、C、D三点。设铣刀外径与螺旋线的切点为B，铣刀与杆类胚料外圆周接触时的点为C，切削完成时铣刀离开杆类胚料时的位置为D。通过对实际的加工过程分析可得B点，C点可能切入点[3-5]。

以上参数建立完成后，铣刀正交车铣杆类胚料时，B，C两点的位置无法确定，C点可能会在B点之上，或者B点之下。因此将这两种情况分开考虑。

(1)当C点在B之上时，以C点为切入点，铣刀刀齿与杆件的啮合区为图1(a)中∠COD；

(2)当C点在B点之下时，以B点为切入点，铣刀刀齿与杆件啮合区为图1(a)中的∠BOD。

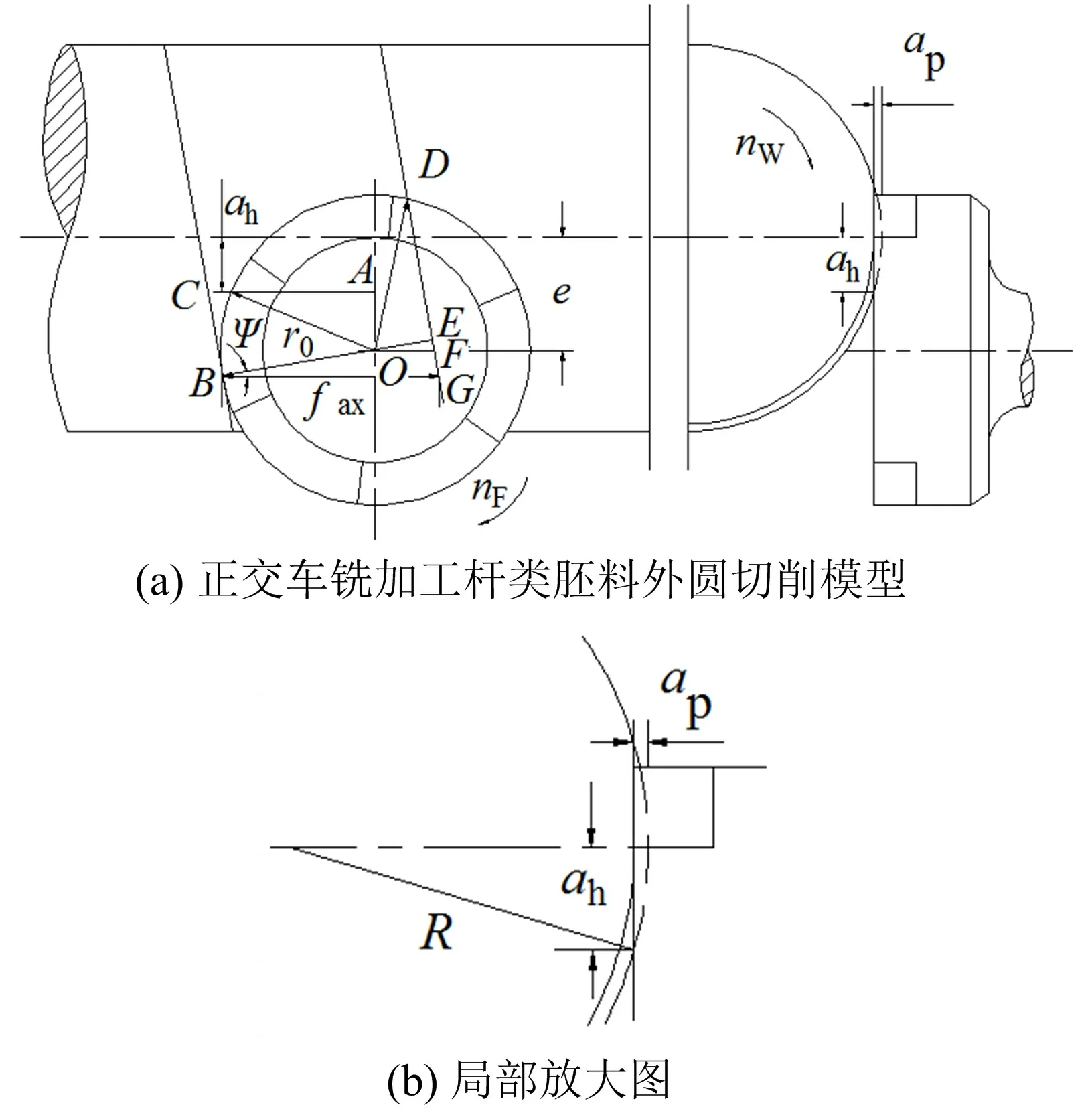
图1 正交车铣杆类胚料外圆切削模型

(1)首先对假设条件1进行分析；

由于点B在点C之下，因此可以将点B视为切点，选取一点E，使直线BE与螺旋线垂直。选取一点G,使∠BEG=90°，因此在△BEG中，∠EBG与螺旋线升角Ψ大小相等，分析可得直线BG为铣刀的轴向进给量fax，通过三角形余弦公式可得:

(1)

由此可以求出直线BE的长度。又因为BO为铣刀的半径，因此可以推导出直线OE的长度。

又因为直线OE于螺旋线向垂直，∠OED=90°，所以可利用反余弦公式

(2)

求出∠DOE的角度。又因为∠EOF与螺旋线升角Ψ相等，所以可求出∠AOD的角度。

设ah为铣刀与杆件接触时已加工表面到未加工表面的距离，即：

(3)

OA为铣刀半径与刀片有效切削刃长度的差再减去ah，OC为刀具半径，运用反余弦公式，求得∠AOC的值，即：

(4)

因此铣刀切削杆件时，切入到切出之间的角度(∠COD)便可由数学知识推出，即∠COD=∠AOC+∠AOD。

(2)当C点在B点之下时

铣刀刀刃切削杆件时，刀刃与杆件接触为从B点到D点，切入到切出之间的角为∠BOD。所以，∠BOD=π-∠DOE。其中，∠DOE的求解与点C在点B之上的求解相同。

在图2中，铣刀的切入角为Φst，由公式5推导出；切出角为Φex。可由公式(6)推导出：

(5)

(6)

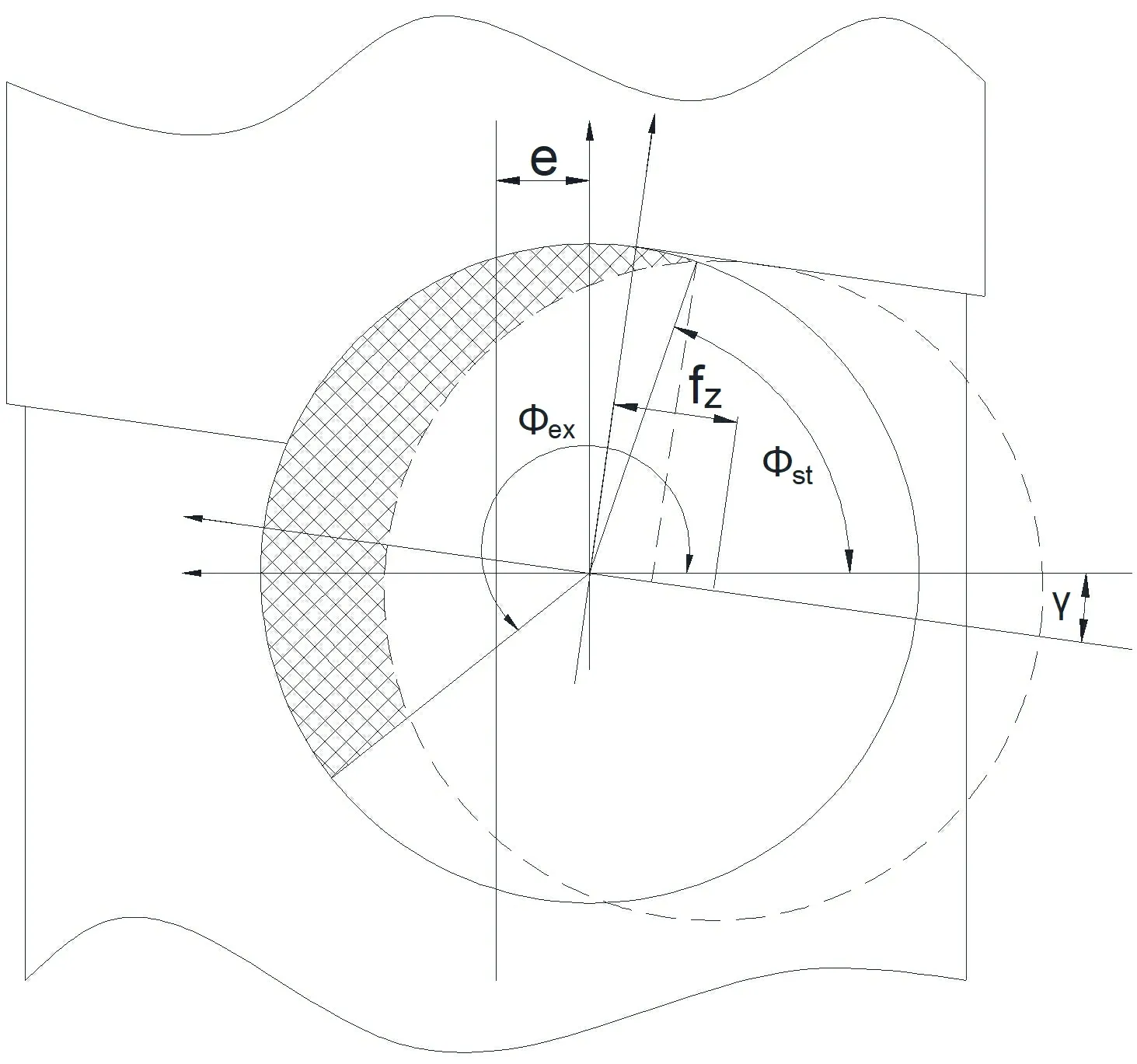
图2 切入切出角几何位置示意图

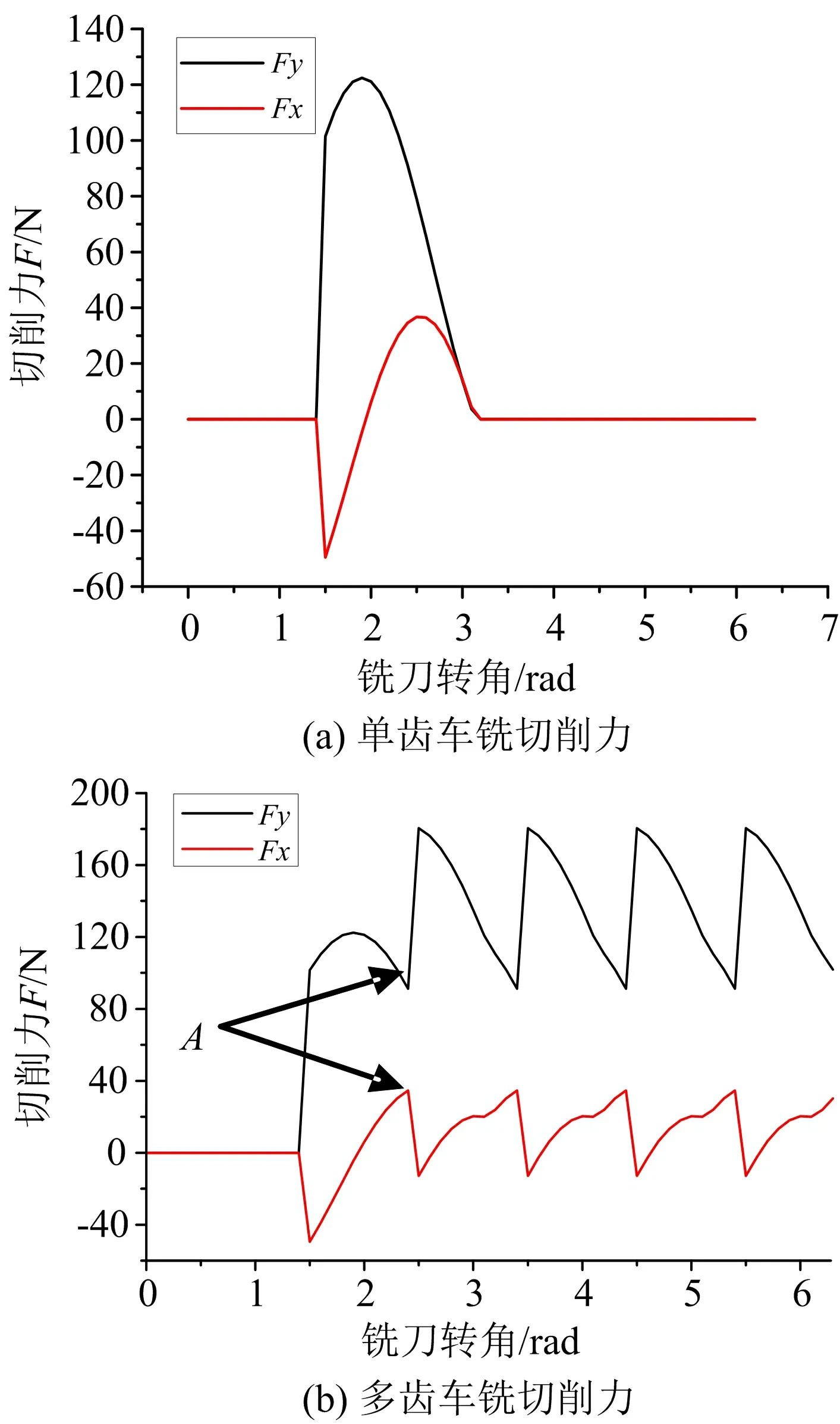
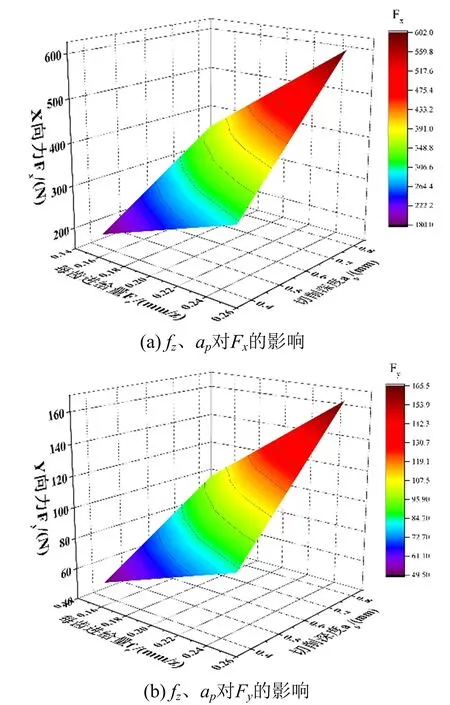
由于铣刀的工作齿数Zc是变化的整数，反映了某一时刻铣刀刀齿参与切削的刀齿数目，Zmax-1

(7)

二、车铣切削力的研究

在正交车铣加工杆类胚料的过程中，同时进行切削的齿数对切削力的大小有着很大的影响。而且同时有多个切削刃参与加工时，切削力合力比单齿切削时大许多，降低了切削工程中的可靠性，十分不利于杆类胚料的高精度加工[6]。因此，研究铣刀同时参与切削的齿数的个数对切削力的控制以及零件的加工质量具有很重要的意义。正交车铣杆类胚料时铣刀同时工作的齿数受多因素的影响。当齿间角大于啮合区范围时，始终只有一个刀齿切削，且存在部分时间刀齿不与工件接触。在齿间角小于啮合区范围时，为多齿同时参与切削情况，同时参与切削的铣刀齿数大于一[7]。

(一)单齿车铣切削力分析

单齿车铣杆件胚料时，切削层是不断变化的。且切削层的公称宽度和主切削刃的长度有关，用bD表示，即：

(8)

公式中：ap—切削深度；Kr—铣刀的主偏角。

用hD表示面铣刀的刀齿在任意位置的切削层公称厚度，即

hD=fzkrcosφ

(9)

根据以上两个公式，可以得到切削层的公称横截面积ADo为：

ADo=hDbD=fzapcosφ

(10)

公式中：φ为铣刀刀尖铣削点的进给方向角；fz为每齿进给量。

面铣刀的法向铣削力FcN、轴向铣削力Fp计算公式如下所示：

(11)

公式中：kc—单位面积铣削力；λ—铣削相关系数。

运用矩阵计算公式将Fp、FcN转换为轴向上的分力Fx和径向上的铣削分力Fy，即：

(12)

进一步计算得：

(13)

(二)多齿车铣切削力分析

多齿切削力的大小和齿间角θ以及同时工作齿数Zc有关。

当铣刀的齿数为Z时，Fx和Fy可以用如下公式来计算：

(14)

选用表1如下切削参数来进行仿真，得到正交车铣杆类胚料单齿、多齿切削时的切削力状态分析如图3所示。

表1 切削参数表

单齿、多齿切削时的切削力状态分析图：

(三)实验结果与分析

如图3a所示，在正交车铣加工杆类胚料的过程中，Fy由0开始，在切入段时急剧增大，切入段铣刀经过大约0.6rad后，达到峰值130N，经过最大值后缓慢减小，并在切出段，切削力逐渐递减为0，且在整个切削周期内，Fy值始终为正值。Fx值的变化相对于Fy稍许复杂些，FX在切入阶段数值沿负方向急剧增大，在达到最大值(负方向)50N后，开始沿反方向快速增大，在铣刀转角2.6rad时达到正向最大值38N后缓慢下降至0。Fx、Fy均在切入阶段波动剧烈，在切出阶段趋于平稳，因此此仿真验证了正交车铣杆类零件的过程中切入工件时冲击剧烈，切出工件时受力平缓[8]。

图3 单齿，多齿切削时切削力变化图

对比图3b，在多齿切削时因为有多个刀齿同时参与切削，故切削力的大小以及变化规律与单齿切削具有明显的差异。切削初期，只有单齿切削，因此切削力的变化与单齿切削同时期相同。当切削过程进行到切削点A时，上一切齿并未退出切削过程，而下一齿已经开始进入切削，因此此时切削力产生了极为复杂，剧烈的变化[9]。FY在减小阶段时，与下一齿的切削力产生叠加导致FY急剧上升，FX的变化与FY类似。通过比对两张仿真图可以得出，多齿切削时，FY变大，波动剧烈；FX减小，波动平缓。

(四)每齿进给量和切削深度对切削力的影响

通过研究分析得出，每齿进给量和切削深度对正交车铣的轴向力和径向力有很大的影响。通过对材料受力的仿真分析，我们发现每齿进给量和切削深度与轴向力和径向力呈如图4所示的正线性关系。但是轴向力的大小对机床进给系统的变形和振动有着直接的关系，因此合理的控制轴向力对零件的加工精度，对表面加工质量有着直接的影响[10]。