灾后无人机不确定偏好序下稳定中继选择方法
2022-02-13徐子蒙王博文王晓琳
徐子蒙,王博文,云 霄,王晓琳
(1.中国矿业大学 信息与控制工程学院,江苏 徐州 221116;2.中国矿业大学 矿业工程学院,江苏 徐州 221116)
2019年,应急管理部发布《应急管理信息化发展战略规划框架》,要求整合无人机(Unmanned Aerial Vehicle,UAV)等空基网络资源,实现对灾害事故易发、多发、频发区域的全方位、立体化、无盲区的灾情监测与通信覆盖。无人机凭借灵活度高、操控方便和可重构性强等特点,能快速保障通信基础设施损毁的受灾地区用户恢复正常通信,可更为高效地完成应急通信任务,因此在应急通信中发挥越来越重要的作用[1-4]。无人机除了作为空中基站覆盖因基础设施损毁产生的通信盲点,还可以作为机会中继改善系统通信性能。考虑到无人机中继辅助基站、车辆和无人机等传输信息,具有扩大通信范围,提高系统吞吐量等优势,国内外学者对此开展了一系列研究[5-9],相关工作的优劣处对比如表1所示。无人机作为中继能增强通信和网络性能,应用日趋广泛,灾害事故对极端环境下应急通信网络快速重组与灾情信息实时回传提出了严峻挑战,因此,在应急通信场景中考虑无人机中继提高应急通信保障能力十分必要。

表1 无人机中继相关工作
匹配理论作为分析用户互利关系的数学工具,被广泛应用于分布式无线资源分配与中继选择算法设计中。文献[10]在D2D(Device-to-Device)通信场景中,利用人际社会关系建立社会稳定匹配模型,实现物理层安全性和吞吐量性能的折中。文献[11]在无人机辅助的车联网中,提出基于GS算法的无人机任务分配方法,最大化用户的利润。在灾后应急通信场景中,为了保障救援人员及时有效沟通,允许多个D2D对复用同一中继无人机,但同时也带来同群效应的问题,因此前述文献中的一对一匹配方法不适用。文献[12]提出了一种交换操作来解决多对一匹配中的同群效应,可文献中提出的算法是集中式的,不适用于分布式场景中。文献[13]提出了双边交换稳定匹配算法,在具有同群效应的动态分布式网络中找到稳定匹配方案。
上述文献的匹配过程需要双边主体间的连接权重等准确信息,而在现实情况中由于决策环境的模糊性和复杂性,匹配双边中一边更容易获得另一边个体的不精确的序区间偏好信息,因此,有学者对基于不完全偏好序、不确定偏好序以及弱偏好序等信息的双边匹配问题展开研究[14-17]。文献[15]针对偏好序值不完全情况下的婚姻匹配问题,采用近似算法得到稳定匹配的数量并提高近似比。文献[16]通过求解弱稳定匹配、α-稳定匹配等的多目标优化模型,获得序区间偏好信息下的最优双边稳定匹配。文献[17]将同群效应引入不确定偏好下的双边匹配模型中,实现最大化满意度并最小化个体间差异的双目标。针对无人机动态飞行且轨迹未知的情况,文献[18]提出了一种中继无人机实时位置调整方法,确保信息可靠传输至地面站。文献[19]提出了一种在线分布式的方法解决了动态网络中的中继选择和信道选择问题。受上述文献启发,结合实际的灾后应急场景,比如地震、火灾等灾害事故导致房屋建筑的坍塌等,产生的遮蔽、浓烟造成应急救援人员难以获取用户的准确位置信息等动态不确定性,展开了灾后无人机不确定偏好下双边稳定匹配中继选择方法的研究工作,主要研究内容如下:
(1) 建立灾后无人机辅助的D2D用户成功传输优化模型,最大化D2D用户的传输成功率。考虑网络的不确定性和该问题是NP难问题,很难直接求解,因此将优化问题转为D2D用户中继无人机选择问题。
(2) 根据D2D用户和中继无人机的不确定偏好序建立D2D用户和中继无人机的偏好列表,首先利用多对一双边稳定匹配理论解决中继无人机选择问题,然后给出了文中的算法步骤、稳定性分析和计算复杂度分析。
(3) 仿真结果表明,笔者所提的带有同群效应的中继无人机选择算法下D2D用户具有很好的数据成功传输性能。与穷举算法、一对一匹配算法以及随机中继选择算法对比,验证了文中方法的有效性。
1 系统模型
1.1 网络模型
如图1所示,无人机在空中执行灾情勘察、信息采集等任务,地面D2D用户(如救援人员、指挥人员等)可以选择无人机协作通信。假设系统中有M架无人机,表示为U={U1,…,Um,…,UM},有K个D2D对,表示为K={1,…,k,…,K},其中一对D2D用户包含一个D2D发射端和一个D2D接收端,分别表示为S={S1,…,Sk,…,SK}和D={D1,…,Dk,…,DK}。任务传输周期划分成T个离散的等间隔时隙,并表示为{1,…,t,…,T},时隙长度为τ,并假设每个时隙长度足够短,在单个时隙内,D2D对可获得的中继UAV和网络中各节点的位置大致不变。LUm(t)=(xUm(t),yUm(t),zUm(t))表示无人机Um的实时位置,则无人机Um在下一时隙t+1的位置为LUm(t+1)=LUm(t+1)+vτ·ωUm(t),v为无人机的飞行速度,ωUm(t)表示无人机Um在时隙t的飞行方向。
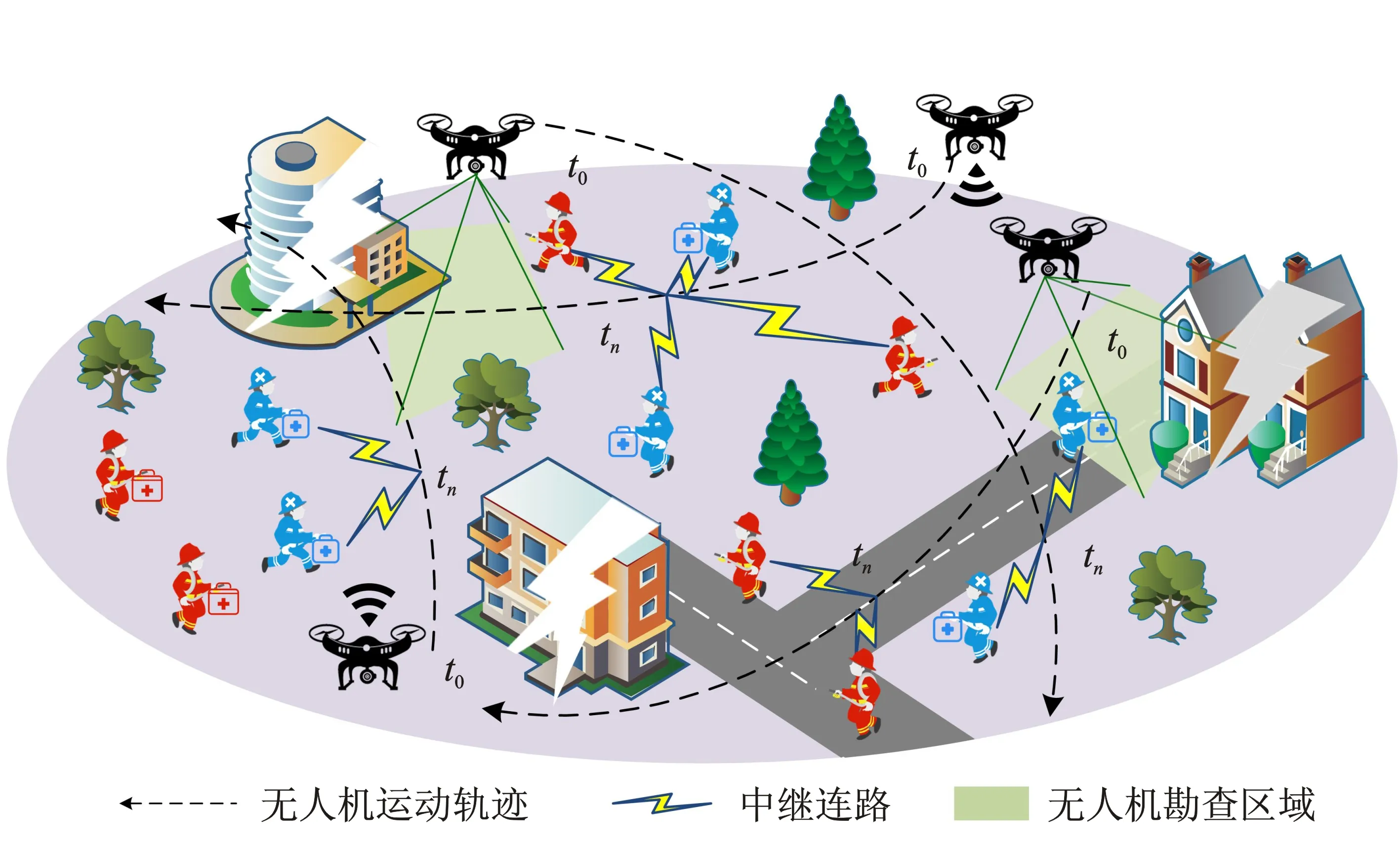
图1 无人机辅助的应急通信场景
假设系统中信道数与中继无人机数目一致。考虑到灾后应急场景对远距离传输的实际需求,为了便于分析中继选择算法的性能,文中假设同一D2D对发射端和接收端之间的传输数据率较低,均需要通过无人机中继辅助传输。如果多个D2D对有相同的无人机选择,无人机采用时分多址接入(Time Division Multiple Access,TDMA)技术来服务这些D2D对,因此不同的无人机服务的D2D对之间的干扰得以避免。
1.2 传输模型
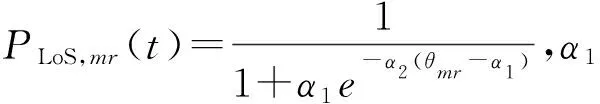
Pavg,mr(t)=PLoS,mr(t)PLLoS,mr(t)+PNLoS,mr(t)PLNLoS,mr(t) ,
(1)
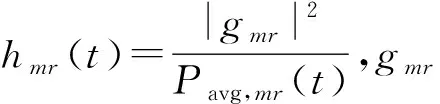
假设每架无人机或每个D2D用户装备单根天线,一架无人机可以协助多个D2D用户传输数据,一个D2D对最多只能选择一架无人机协助传输数据。当存在多个D2D用户选择相同的无人机时,D2D用户机会均等地共享信道资源。D2D对k有大小为fk的数据需要传输,数据包逐帧传输,每帧的长度均相等。一帧分为2个阶段:阶段1,发射端Sk将数据传输至中继无人机Um;阶段2,中继无人机Um将数据传输至接收端Dk。在中继传输模式下,采用解码转发(Decode-and-Forward,DF)协议进行数据传输。因此,在t时隙,D2D对k的发射端Sk通过无人机Um传输至接收端Dk的数据速率为
(2)
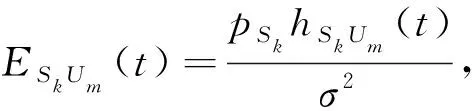
2 问题表述
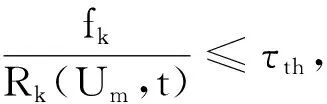
网络的动态特性导致数据速率在不同时隙可能不同,从而成功传输的D2D对数量可能不同,因此,通过优化实时中继无人机分配最大化D2D用户的平均总传输成功率,即最大化网络中传输成功的D2D对数量与D2D对总数比值在整个传输周期的平均值:
(3)
s.t.amk(t)∈{0,1},bmk(t)∈{0,1} ,
(4)
(5)
其中,限制条件式(4)表示amk(t)和bmk(t)为二进制数。限制条件式(5)表示每个D2D对至多能选择一架无人机作为中继,每架无人机至多可协助q0(Um)个D2D对传输数据。
该优化问题是NP难问题,并且解决难点有以下几个方面:首先,由于无人机动态飞行,位置实时变化,因此最佳无人机中继分配是随时间变化而变化的;其次,无人机的飞行轨迹是由它们的任务决定的,对于地面用户来说是未知的,因此,离线规划方法不可取,需要在线方法。下面将优化问题转为中继选择的优化进行求解。
3 实现方法
在经典的匹配模型中,匹配双方可以根据确定的偏好列表信息决定匹配策略,但在灾后场景中,无人机和D2D用户的动态位置可能导致匹配策略的不确定性,因此,仅根据在某些时刻的传输性能得到的匹配策略是不准确的,要分析基于偏好不确定性匹配博弈的中继无人机选择问题。针对多对一双边匹配中存在同群效应的问题,需进一步对相应的匹配结果进行交换操作解决。
3.1 确定偏好序下的双边匹配
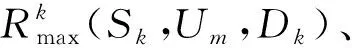
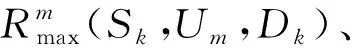
(6)
(7)
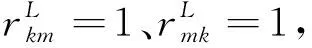
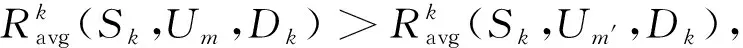
为了解决式(3)中的问题,笔者运用博弈论中双边匹配知识。匹配理论允许每个参与者(D2D对和无人机)定义各自的效用,可以分布式解决中继无人机选择问题。受经济学中毕业生与实习医院相匹配问题[24]的启发,本文将D2D用户的中继无人机选择问题定义为多对一匹配博弈,即双边匹配是在D2D对集合中的元素与中继无人机集合中的元素之间进行多对一的匹配。传统的匹配问题需要匹配双方建立完整精确的偏好列表,实际情况中,灾后环境的复杂性、无人机和D2D用户的移动性以及参与者数量较多等因素,容易导致匹配双方的偏好列表具有不完整性[14]和模糊性[17],因此提出基于不完整不确定偏好序的多对一匹配算法。先给出如下多对一匹配定义:
定义1给定两个不同的有限参与集合K和U,ω定义为多对一匹配关系,一个匹配是满足以下条件的双映射ω:K∪U→K∪U∪∅:① ∀k∈K,ω(k)⊆U∪∅,|ω(k)|≤1;② ∀Um∈U,ω(Um)⊆K∪ ∅,|ω(Um)|≤q0;③ ∀k∈K,∀Um∈U,ω(k)=Um⟺ω(Um)=k。
为了得到匹配结果ω,无人机与D2D用户双方根据偏好关系对另一方降序排列形成偏好列表N,匹配的对象在各自偏好列表中越靠前,相应地在系统中获得的利益也越大。根据上述双边匹配模型,提出基于不确定偏好序的多对一匹配算法(UMA)。在每个时隙,D2D用户通过预测中继无人机的位置来计算传输性能,得到不确定偏好序,在此基础上综合评估生成相应的偏好列表。D2D用户根据偏好列表,对中继无人机进行排序和选择。中继无人机收到D2D用户的请求后,在满足配额约束要求下,接受最佳候选者的匹配请求,拒绝其他的D2D用户。被接受的D2D用户停止匹配过程,而被拒绝的D2D用户继续向次优中继无人机发出匹配请求。过程不断迭代,直到D2D用户被中继无人机匹配或拒绝,由于偏好列表可能不完整,匹配结果可以是部分匹配。相应的过程见算法1。
算法1基于不完整不确定偏好序的多对一匹配算法(UMA)。
输入:U,K,t,q0(Um)。
loop fort=1,…,T
fork∈K和Um∈U分别对在各自探测范围内的UAV和D2D do
构建偏好列表Nk和Nm;
while ∃k∈K,|ω(k)|=0,且Nk≠∅ do
for 所有k∈Kdo
向位于Nk第一位的中继无人机Um*发送请求;
将bm*k设置为1,更新Nk=Nk/Um*;
end for
for 所有Um∈Udo
if 当前请求数量>q0(Um) then
Um根据Nm,接受q0(Um)个D2D对,拒绝其他的D2D对;
被拒绝的D2D对bm*k值设置为0;
else
Um接受当前所有的请求者;
end if
end for
end while
end for
for未匹配的k∈K和Um∈Udo
等待t+1时隙用户动态加入
end for
返回匹配结果ω(t);
end loop
输出:匹配结果ω(t)。
基于不确定偏好序的多对一匹配算法中参与匹配的D2D对和无人机的数量分别为K和M,在最坏情况下,任意D2D对的候选中继集合中都包含所有的无人机,所有的中继无人机对D2D用户的偏好都不满足中继无人机的要求,在这种情况下参与匹配的D2D用户需要不断地向其他中继无人机发送请求并被拒绝,因此算法的最坏时间复杂度为O(MK),在系统整个任务传输周期算法的最坏时间复杂度为O(TMK)。
复用同一中继无人机的D2D对数量会根据算法的匹配结果不同而不同,导致D2D用户的传输速率发生变化,相应的偏好列表改变,因此D2D用户可能会出现相较于当前的匹配对象,更喜欢其他中继无人机的情况,故不确定偏好序下的多对一匹配算法的匹配结果是不稳定的。为了得到稳定的匹配结果,D2D用户既要关注无人机的选择情况,也要关注复用同一无人机中继的D2D对情况,即需要考虑同群效应的影响。
3.2 带有同群效应的中继无人机选择算法
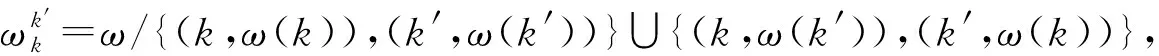
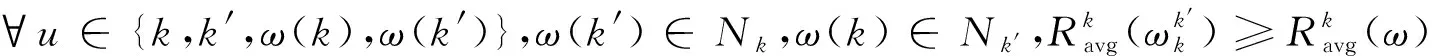
由定义2可知,交换匹配是在交换限制对之间进行的。交换后,所有参与交换的D2D对的传输速率不会降低,而至少其中一个D2D对的传输速率会增加,这同时也避免了在等价匹配之间循环。交换操作在效用值的基础上进行,基于预测范围内的速率增加作为交换条件体现出传输过程中的不确定性。
定义3对于多对一双边匹配ω,如果不存在交换限制对,则称匹配ω是双边交换稳定的。
双边交换稳定性概念与传统稳定性概念[24]相比有所不同,这与D2D对和中继无人机根据实际匹配状态动态的改变偏好策略有关。如前所述,同群效应的存在使得匹配结果不稳定,需要进行交换匹配来消除同群效应的影响。然而,在分布式方法中,并不能像集中式方法那样直接对交换限制对中的用户进行交换[13]。因此,提出算法2,即带有同群效应的中继无人机选择算法(UMPA),对算法1中匹配结果ω(tn)的交换限制对迭代完成每个交换操作,最终得到双边交换稳定匹配结果,相应的过程见算法2。
算法2带有同群效应的中继无人机选择算法(UMPA)。
输入:算法1中匹配结果ω(t),K,U,q0(Um)。
初始化D2D对k向k′发送交换请求的次数,即Ckk′=0;
Repeat
每个D2D对k∈K搜索另一个D2D对k′∈{K/k}以形成交换限制对;
if(k,k′)形成交换限制对,并满足Ckk′+Ck′k≤2 then
根据算法1更新匹配结果ω(t),Ckk′=Ckk′+1;
else
保持当前的匹配状态;
end if
直到当前匹配中不存在任何交换限制对;
end Repeat
输出:更新后的匹配结果ω(t)。
在算法2中,将Ckk′表示为D2D对k向k′发送交换请求的次数,且k最多可与k′交换2次,这避免了乒乓效应,保证了算法收敛[13]。当前匹配中不存在任何交换限制对时,交换匹配过程结束,更新匹配结果ω(t)。下面分析算法的稳定性和计算复杂度。
①稳定性:提出的算法最终得到的匹配ω是双边交换稳定的。
证明:假设最终得到的匹配结果ω不是双边交换稳定的,则至少存在一个交换限制对(k,k′),但双边交换稳定匹配中继选择算法在存在交换限制对的情况下是不会终止的,因此,该匹配结果ω不是最终结果,与假设条件冲突。因此,文中所提算法得到的匹配是双边交换稳定的。
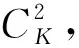
4 仿真分析
使用MATLAB R2015a工具对提出的算法进行100次独立重复仿真实验仿真,并采用与其他方案对比的方式评价笔者所提算法的性能。D2D对随机分布在3 km×3 km区域内,发射端与对应的接收端之间的距离随机取值于(100 m,200 m)以内,且发射端与接收端用户每个时隙随机在(1 m,2 m)范围内移动。无人机随机选择飞行方向,且不飞出规定区域。部分仿真参数设置如表1所示,与郊区环境不同[18],考虑城市环境,综合分析城市地形和建筑高度,将UAV飞行高度设置为[100 m,500 m]。
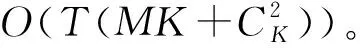
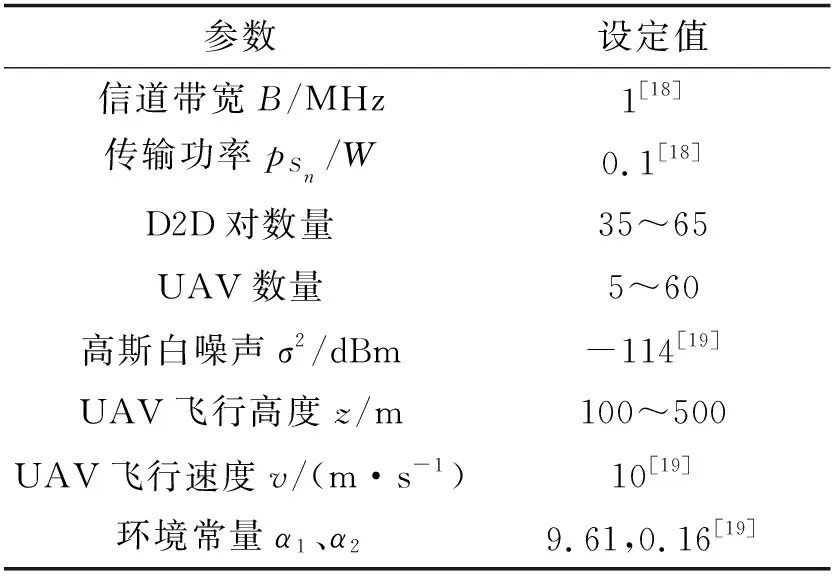
表2 实验仿真参数
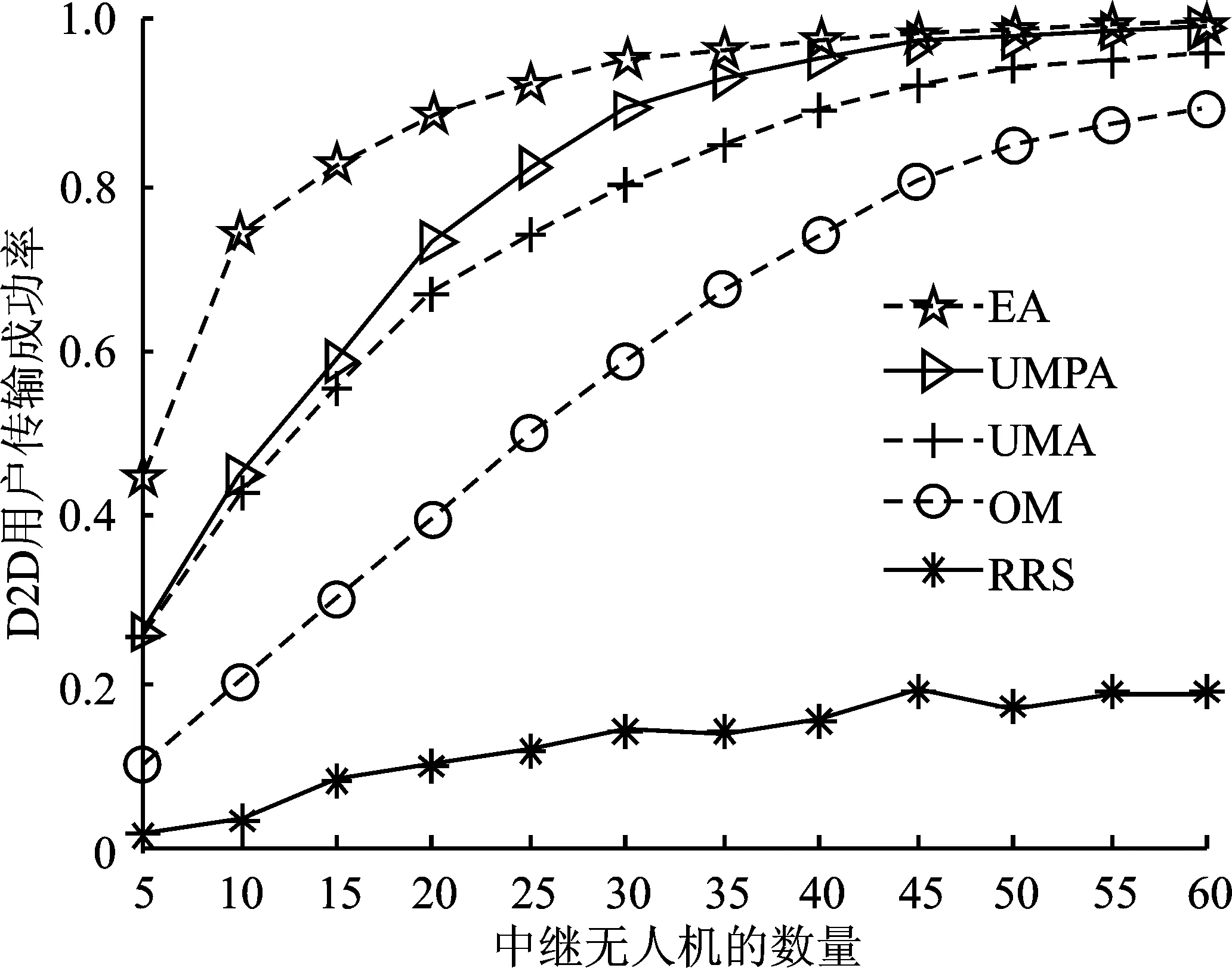
图2 D2D用户传输成功率随中继无人机数量变化的关系
图2是在K=50时D2D用户传输成功率随中继无人机数量M的变化曲线。图3是在M=10时D2D用户传输成功率随D2D对数量K的变化曲线。图2和图3中D2D用户传输数据期望值为0.5 MB,多对一匹配算法中无人机配额设置为5。由图2可知,随着中继无人机数量的增加,中继无人机协作的D2D对数量增加,并且D2D用户选择性能更优的中继提高传输成功率的机会更大,D2D用户传输成功率随着中继无人机数量的增加而增加。由于偏好列表不完整,中继无人机数量达到50之后,EA算法和UMPA算法的D2D用户传输成功率逐渐接近1。EA算法从D2D用户选择中继无人机的所有情况中得到最佳的分配结果,因此D2D用户传输成功率最高。文中所提算法能够实现D2D用户和中继无人机间的多对一匹配,能让更多的D2D用户同时进行通信,因此D2D用户传输成功率高于OM算法。RRS算法虽然是多对一匹配算法,但是RRS算法忽略了用户偏好的指向性,与文中所提算法相比,更易于为D2D用户分配通信质量差的中继无人机,因此D2D用户传输成功率低。当M=30时,UMPA算法的D2D用户传输成功率低于EA算法约7%,高于UMA算法1约12%、OM算法约52%和RRS算法约533%。从图3中可知,随着D2D用户数量的增加,D2D用户传输成功率呈递减的趋势。原因是D2D用户传输成功率为成功传输的D2D对数与D2D对总数的比值,当中继无人机可协助的D2D对数一定时,D2D用户数量增多,传输成功率降低。当K=35时,UMPA算法得到的D2D用户传输成功率低于EA算法约30%,高于UMA算法约25%、OM算法约79%和RRS算法约462%。
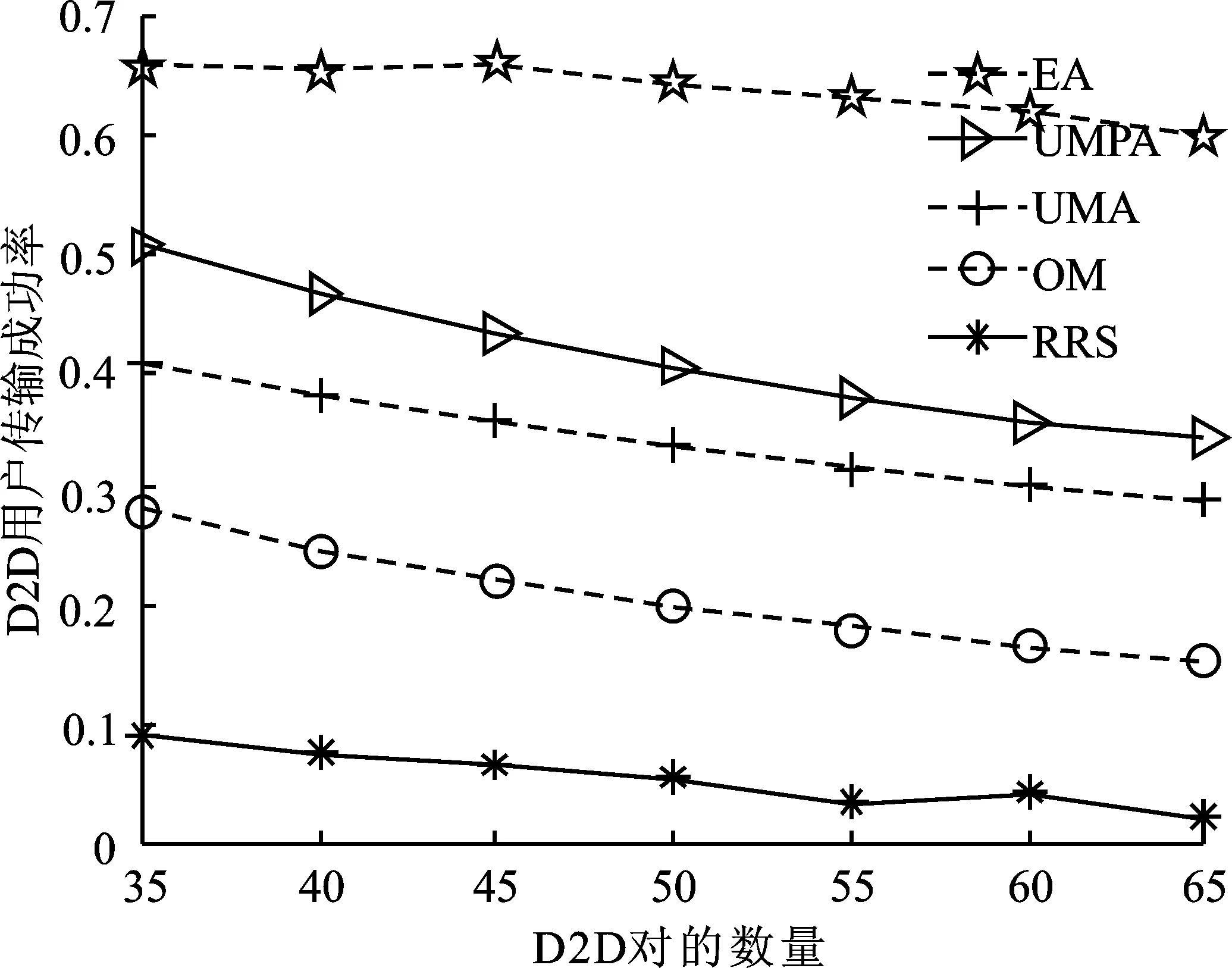
图3 D2D用户传输成功率随D2D对数量变化的关系
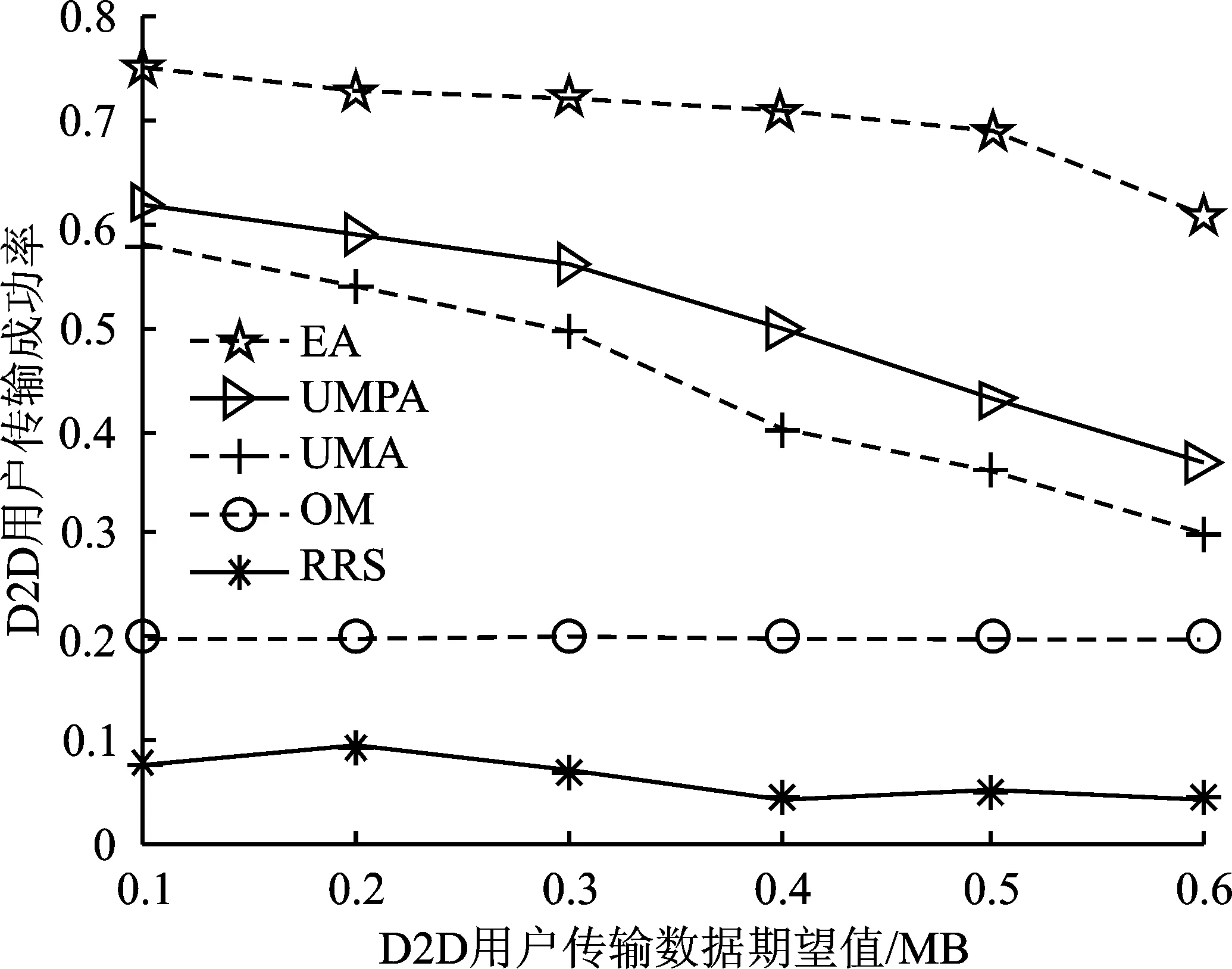
图4 D2D用户传输成功率随传输数据期望值变化的关系
图4是在K=50,M=10的条件下D2D用户传输成功率随传输数据期望值的变化曲线。多对一匹配算法中无人机配额设置为5。D2D用户传输数据期望值越大,对传输速率的要求越高,EA算法和多对一匹配算法下的D2D用户传输成功率逐渐减小。多对一匹配中受同群效应影响,D2D用户的平均传输速率会小于OM算法中的D2D用户的平均传输速率,满足成功传输要求的D2D用户减少,而OM算法中不存同群效应,D2D用户的平均传输速率相对较高,满足成功传输要求的D2D用户数相等,因此传输成功率保持不变。当数据期望值为0.5 MB时,UMPA算法得到的D2D用户传输成功率低于EA算法约60%,高于UMA约19%、OM算法约115%和RRS算法约746%。
图5和图6是在K=50,M=10的条件下D2D用户传输成功率分别随无人机配额q0和探测范围的变化曲线。D2D用户传输数据期望值为0.5 MB。从图5中可知,笔者所提算法的D2D用户传输成功率随着无人机配额的增加先增大后减小,原因是当无人机配额小于5时,随着无人机配额数的增加,无人机可协助的D2D用户数越多,而D2D对总数一定,D2D用户传输成功率上升。当无人机配额大于5时,无人机可协助的D2D对数超过网络中D2D对总数,多对一匹配算法的D2D用户的传输速率随着相关的D2D用户增多而减小,满足成功传输要求的D2D用户减少,传输成功率降低。EA算法包含满足无人机配额约束下D2D对所有可能的中继无人机选择情况,因此传输成功率最高。OM算法中不考虑无人机配额限制,因此传输成功率保持不变。特别地,当无人机配额为1时,多对一匹配算法退化为一对一匹配算法。当q0=5时,UMPA算法得到的D2D用户传输成功率低于EA算法约37%,高于UMA约10%、OM算法约170%和RRS算法约896%。图6中,随着无人机与D2D装备雷达探测范围的扩大,偏好信息越完整,多对一算法下参与数据传输的D2D用户增多,D2D用户传输成功率上升。OM算法中无同群效应,匹配到中继无人机的D2D用户数据速率高,因此在探测范围为1 500 m后D2D用户传输成功率稳定保持在0.2左右。当探测范围为 2 000 m 时,UMPA算法得到的D2D用户传输成功率低于EA算法约20%,高于UMA约13%、OM算法约249%和RRS算法约221%。
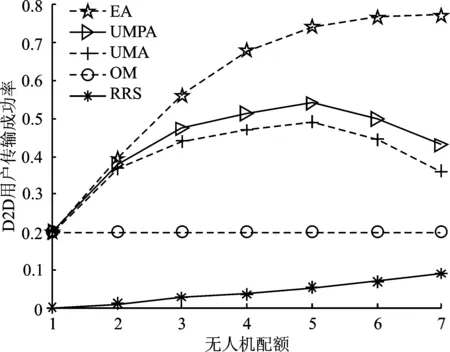
图5 D2D用户传输成功率随无人机配额变化的关系
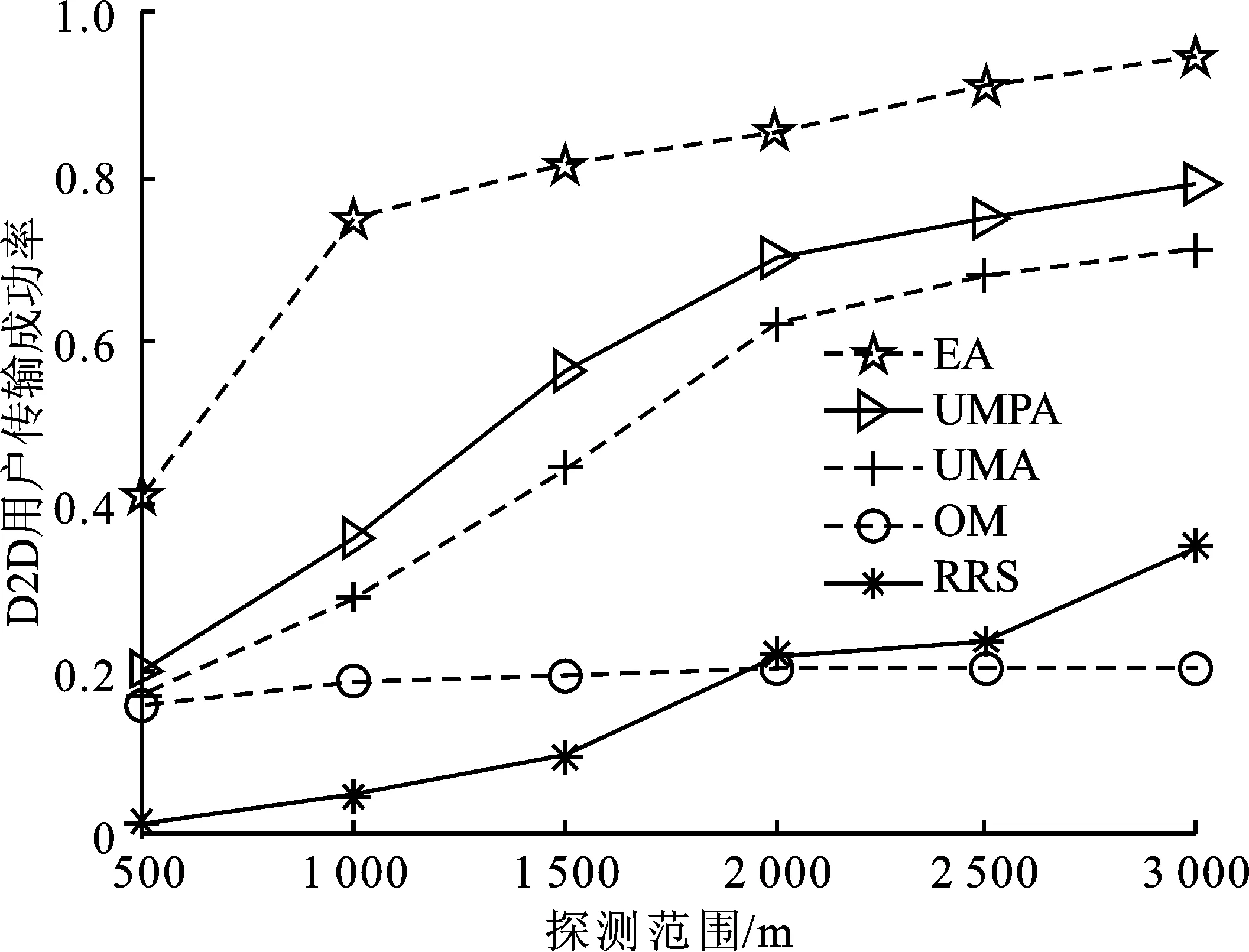
图6 D2D用户传输成功率随探测范围变化的关系
进一步分析实验结果,EA算法搜索D2D用户选择中继无人机的所有情况,并从中得到最佳的分配结果,因此D2D用户传输成功率最高。RRS算法能在极短的决策时间内给出中继决策方案,适用于网络拓扑快变场景,但由于随机选择忽略了用户偏好的指向性,且在偏好列表不完整的情况下,极有可能匹配到传输成功概率较低的链路,难以实现问题的最优化,因此D2D用户传输成功率较低。OM算法考虑了用户偏好的指向性,且算法中不存在同群效应,因此单个D2D用户的数据速率高,但是匹配成功的用户少,多个D2D用户无法传输,导致总的传输成功率低。UMA算法和UMPA算法中存在同一时隙多个D2D用户均等分享同一无人机资源的情况,单个D2D用户的数据速率会低于OM算法。UMPA算法中考虑了同群效应,通过交换匹配保证了结果的稳定性,进一步优化了D2D用户传输成功率,因此算法性能优于UMA算法。综上所述,相较于EA算法,笔者所提算法复杂度更低。与RSS算法相比,所提算法的匹配结果具有稳定性,且能得到较高的D2D用户传输成功率。对比于OM算法,所提算法下中继无人机利用率高,能使用较少的中继无人机得到较高的D2D用户传输成功率。因此,笔者所提算法性能是优于其他对比方法的,且更能满足动态应急通信场景的需求。
5 结束语
笔者研究了灾后应急通信场景中D2D通信系统的无人机辅助中继选择问题。考虑网络中无人机的轨迹未知和D2D用户动态移动性等导致的不确定因素,首先提出一种基于不确定偏好序的带有同群效应的多对一匹配中继选择算法,并通过交换匹配消除同群效应的影响,然后从稳定性和复杂度等方面综合分析算法的性能。从仿真结果上看,笔者提出的算法得到的D2D用户传输成功率虽然低于穷举算法的传输成功率,得到次优的结果,但是所提算法的计算复杂度较穷举算法大幅度降低,并且所提算法允许同一中继无人机在同一时隙协作多对D2D用户进行通信,保障救援人员及时有效沟通。总体来说,所提算法具有复杂度低、稳定性强和无人机利用率高的性能优势,更适用于应急动态分布式场景。
