航发轴承复合故障诊断的循环维纳滤波方法

张伟涛，纪晓凡，黄 菊，楼顺天

(1.西安电子科技大学 电子工程学院，陕西 西安 710071；2.中国航发贵阳发动机设计研究所，贵州 贵阳 550081)

滚动轴承是航空发动机以及其它装备的核心旋转部件。由于航空发动机主轴轴承长期工作在高温、高速、重载的严苛工况下，因此前期出现的微小故障将很快演变为严重故障，从而对飞行安全造成重大威胁。对航发主轴轴承的运行状态进行连续监测，并及时检测潜在的故障是提高旋转设备可靠性与安全性的关键。目前，航发主轴轴承故障诊断的难点在于强背景噪声和其它干扰信号的影响，尤其是当存在复合故障时，采集的振动信号成分将变得更为繁杂，这给复杂工况下的主轴轴承故障诊断带来了更大的挑战。

近年来，针对滚动轴承复合故障诊断问题提出了很多方法[1-5]，包括传统频谱分析方法、谱峭度方法、盲信号分离方法、盲信号提取方法以及智能诊断方法等。传统包络谱分析方法通过从包络谱中直接读取故障特征频率确定故障类型，然而在复杂工况下，主轴轴承的微弱故障频率成分很可能被背景噪声或其它强振动干扰所淹没，因此传统的包络谱分析方法往往失效。最大相关峭度解卷积(Maximun Correlated Kurtosis Deconvolution，MCKD)方法[6-8]把相关峭度最大值对应的信号视为干扰成分，提取出指定周期的解卷积信号。然而，最大相关峭度解卷积算法对参数的取值非常敏感，这极大地限制了其实际应用。典型的盲信号提取方法的信号提取顺序是无法确定的，更无法利用先验信息提取感兴趣的信号。基于数据驱动的智能诊断方法也已经被应用于轴承故障诊断领域，主要包括浅层机器学习模型和深层机器学习模型。浅层机器学习模型如人工神经网络和支持向量机[9-12]，其原理是人工提取一系列的振动信号特征(例如方差、能量熵、均方根等)，将提取的特征作为模型的输入，并结合标签对模型进行训练，从而实现故障诊断。但这类方法的故障诊断效果严重依赖特征的选择，复杂工况下选择具有明显区分度的特征非常困难。深度学习方法[13-19]避免了依靠人工经验进行的特征提取，网络模型在海量数据中自动寻找特征，有更高的泛化性。但深度学习方法需要大量的训练数据，而航发主轴轴承转速和载荷变化快且范围广，要获得复杂时变工况下的海量数据几乎是不现实的。

需要指出的是，采集的航发主轴轴承振动信号通常是包含不同振动源的混合信号。原因主要有两点，其一是长期运行的航发主轴轴承出现的故障往往是复合故障，例如异物进入滚道很可能同时造成内圈和外圈划伤，因此采集的振动数据往往包含不同故障源的振动信号；另一个原因是由于发动机内部结构的复杂性以及高温环境的限制，在实际工况下，用于轴承状态监测的传感器一般不能安装到轴承座或其附近的其它固定位置，而只能布置在机匣上，因此每个传感器采集的振动信号往往是轴承和其它部件振动的综合反映。

考虑到航发主轴轴承复合故障分析的特殊性，在诊断具体故障类型之前有必要对信号进行滤波处理。循环维纳滤波器是一种基于循环平稳信号的谱相干理论提出的，以最小均方误差为最优准则的线性滤波器，已有学者将循环维纳滤波器应用于滚动轴承复合故障诊断问题中[20-22]，其主要思想是将复合故障信号按照特征循环频率进行一组频移，通过一个滤波器组，对信号实现自适应滤波，根据滤波器输出信号和期望信号之间的差值调整滤波器组的权值。

循环维纳滤波算法中，期望信号是影响滤波效果的关键因素。目前主要可以通过典型循环维纳滤波法和人工合成循环维纳滤波法这两种方法获得期望信号。典型循环维纳滤波方法[20]将输入信号直接作为期望信号；这种方法在轴承单一故障诊断时是有效的，但在轴承存在复合故障的情况下，采集的信号中将同时存在多个故障对应的特征频率成分，若仍采用输入信号作为期望信号，那么循环维纳滤波只能抑制部分平稳噪声，而无法提取混合信号中的单一故障成分，使复合故障诊断变得困难。人工合成循环维纳滤波方法[22]首先对采集信号进行循环谱分析，再利用循环频率和单一故障信号生成模型经人工合成得到期望信号；这种方法的分析效果严重依赖循环频率和单一故障信号模型中参数的选取。故障信号模型中的轴承振动固有频率是一个重要参数，轴承固有振动是由于滚动体与内外圈的冲击而产生的，轴承自由状态下的固有频率由轴承组件的材料和尺寸等因素决定，而且还受到安装状态的影响，实际工作中的固有振动频率一般在数千赫兹到数十千赫兹，这使得在实际应用时人工合成的单一故障信号固有频率往往与实际采集信号的固有频率不相符，从而导致复合故障分析效果不佳。

针对上述问题，笔者提出了一种航发主轴轴承复合故障诊断的循环维纳滤波方法。首先通过将CCA准则盲提取结果作为期望信号，对期望信号中的故障特征进行增强；再将采集到的混合振动信号作为滤波器的输入信号，通过循环维纳滤波得到输出信号；最后结合包络谱对输出信号进行故障类型分析，实现复合故障的诊断。通过仿真及实验验证了所述方法的可行性、有效性及相对于现有方法的优点。

1 轴承复合故障信号的数学模型

滚动轴承的故障类型一般按照故障点所处的轴承部件分为：外圈故障、内圈故障、滚动体故障以及保持架故障等。在这些故障类型中内外圈故障较为常见，而且多为复合故障，例如微小刚性异物进入轴承一般会同时在内外圈滚道上造成缺陷。由于航发主轴轴承工作环境的特殊性，振动传感器一般不能直接布置在距离轴承很近的位置，只能布置在轴承外部的非旋转部件或机匣上，若轴承存在复合故障，那么传感器采集的振动信号往往是多个故障点分别引起的振动和其他振动源振动的综合反映。信号采集过程如图1所示。

图1 轴承复合故障信号采集示意图

某一采集通道的信号可表示为

(1)

其中，xi(t)是第i个传感器采集得到的信号，sj(t)是第j个振动源产生的信号，这些独立振动源包括轴承外圈故障点、内圈故障点及滚动子故障点等故障源，也包括机械结构各部件间耦合引起的振动，aij是第j路振动源信号到第i个传感器的路径衰减系数，由于多个传感器安装的位置不同，因此各路径的衰减系数往往也是不同的。假设有N个独立振动源，M个传感器，那么采集到的轴承复合故障信号可以写作

x(t)=AS(t) ，

(2)

其中，x(t)=[x1(t)，…，xM(t)]T，表示采集到M路轴承复合故障信号；S(t)=[s1(t)，…，sN(t)]T，表示N个振动源形成的源信号；A是M×N混合矩阵，它包含了不同振动源到多个传感器的路径衰减系数，一般是未知的。因此航发主轴轴承的复合故障诊断需要首先将故障信号从采集到的混合信号中恢复出来，然后再进行分析。

2 复合故障信号的循环频率

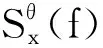
(3)

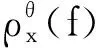
(4)

(5)

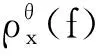
(6)

轴的高速旋转往往导致轴承故障信号具有循环平稳的特性，这可以由故障信号的循环频率来表征，不同类型的故障具有不同的循环频率，也称为故障特征频率。因此可以利用故障特征频率来提取特定的故障信号。 内外圈故障特征频率可由下式计算：

(7)

(8)

其中，fi为内圈故障特征频率，fo为外圈故障特征频率，n为轴承转速，β为接触角，Dm为节圆直径，z为钢球数量，d为钢球直径。

根据故障信号的循环平稳特性，故障信号在循环频率对应的时延处具有最大的自相关。因此，维纳滤波器中的循环频率应取目标故障信号的故障特征频率。

3 基于CCA盲提取的循环维纳滤波器

3.1 现有循环维纳滤波器的不足

循环维纳滤波器是平稳随机信号在最小均方误差意义下的最优滤波器，其结构框图如图2所示。

图2 循环维纳滤波器的结构框图

首先从采集到的M路轴承复合故障信号x(t)=[x1(t)，…，xM(t)]T中选择某一路信号xm(t)的一组频移形式xmη(t)=xm(t)ej2πtη，η∈{θ0，θ1，…，θ(L-1)}作为输入信号，输入信号xmη(t)经过一个滤波器组hmη(t)滤波后得到输出信号ymη(t)，将所有ymη(t)求和，得到总输出y(t)：

(9)

通过对比输出信号y(t)和期望信号γ(t)得到误差信号e(t)，以e(t)的均方值作为代价函数，

E{e2(t)}=E{[γ(t)-y(t)]2} 。

10)

根据最小均方误差算法调整滤波器组的权值，得到循环维纳滤波器滤波器组的递推公式，即

h(t+1)=h(t)+λhe(t)x*T(t) ，

(11)

其中，λh为步长，通过迭代计算得到最优的循环维纳滤波器。

循环维纳滤波器的滤波效果很大程度地受所选取期望信号γ(t)的影响。现有期望信号选取方法主要有两种：一是利用混合的振动信号本身作为期望信号的典型循环维纳滤波方法，但是这种方法只能提高单一故障的振动信号的信噪比，不能从复合故障振动信号中提取出单一故障源信号，因此这种方法只适用于滚动轴承单一故障的诊断，不适用于复合故障诊断；二是人工合成循环维纳滤波方法，这种方法利用循环频率和单一故障信号生成模型，经人工合成得到期望信号，这种方法虽然适用于滚动轴承的复合故障诊断，但该生成模型依赖于轴承转速、接触角等先验信息，在轴承实际运行时这些参数不易获取而且不是固定不变的，利用这些信息人工生成的期望信号的故障特征频率往往与实际采集到的故障特征频率不同，因此利用此信号作为期望信号的滤波结果不能体现出真实的故障源信号。针对现有方法中的缺点和不足，笔者提出了采用CCA盲提取得到的故障特征信号γ(t)作为循环维纳滤波的期望信号。参考图2，从采集到的M路轴承复合故障信号x(t)=[x1(t)，…，xM(t)]T中提取故障特征信号γ(t)，并作为循环维纳滤波器的期望信号，迭代计算后得到的维纳滤波器的输出信号即为单一故障源信号。

3.2 基于CCA的期望信号盲提取方法

笔者提出了CCA准则的盲提取方法，提取出的故障特征信号能反映混合信号中真实的轴承故障特征，将此信号作为循环维纳滤波的期望信号，可以克服现有技术在复合故障诊断中的缺点。盲信号提取的目标就是要设计一个提取向量w，使提取出的信号

γ(t)=wTx(t) ，

(12)

为某一源信号的副本。笔者提出的CCA盲信号提取方法，其基本思想是：任何不相关信号的和的自相关不超过单个信号自相关的最大值，因此基于CCA准则的盲信号提取等价于如下优化问题：

(13)

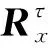
τi=1/fi，

(14)

同理，对于其他不同类型的故障信号提取可以选取其对应的时延。为了提高上述优化问题的收敛速度和可靠性，本文提出了共轭梯度算法对上述问题进行优化求解。

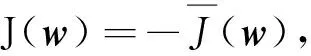
d(1)=-∇w(1)J[w(1)]=-g(1) 。

(15)

当t>1时，搜索方向(1)是在当前最速下降方向-g(1)上进行修正，得到

d(1)=-g(1)+ρ(t-1)d(t-1) 。

(16)

为了确保搜索方向d(t)与d(t-1)关于Hessian矩阵H互为共轭方向，修正系数ρ(t-1)须满足如下共轭条件：

dt(t)H(t-1)d(t-1)=0 。

(17)

将式(16)代入式(17)，得到

(18)

得到了共轭梯度搜索方向d(t)后，便可以对盲提取向量w按如下公式完成更新：

w(t+1)=w(t)+λw(t)d(t) ，

(19)

其中，λw(t)表示迭代步长。为了使共轭梯度算法能够更快收敛，迭代步长λw(t)应满足

(20)

令φ[λw(t)]=J[w(t)+λw(t)d(t)]，那么最优迭代步长应满足d{φ[λw(t)]}/d[λw(t)]=0，即

dT(t)∇wt+1J[w(t+1)]=0 。

(21)

因此，最优步长λ′w(t)按下式计算：

(22)

将CCA盲提取得到的故障特征信号作为循环维纳滤波的期望信号，与现有方法相比，基于CCA盲提取的改进循环维纳滤波器可以通过选取不同的时延和循环频率恢复不同的故障源信号。因此适用于滚动轴承的复合故障诊断，且由于期望信号是从采集到的混合信号中提取得到的，期望信号中包含真实的故障特征频率成分，故使用这种期望信号的循环维纳滤波可以得到真实的故障源信号。

4 仿真与实验结果

本节分别通过仿真和实验数据验证循环维纳滤波方法在轴承复合故障诊断中的有效性。在仿真中，采用了西储大学的故障轴承振动数据[23]，通过随机生成的混合矩阵来模拟实际中不同故障源信号的混合过程。实验中，在航发轴承试验机上采集了具有复合故障的航发主轴轴承振动信号。以上人工混合和实测数据均使用提出的算法进行了故障诊断。

4.1 仿真结果

在仿真中，分别选取西储大学的轴承数据集中几种不同类型的单一故障滚动轴承振动信号作为源信号，信号采样率为12 kHz，主轴转速为1 797 r/min(转/分钟)，其时域波形和包络谱如图3所示。图3 (a)为时域波形，图3 (b)中横轴表示频率，纵轴表示幅值，图中4路信号从上到下依次对应内圈故障信号、无故障信号、外圈故障信号和噪声信号。在源信号中加入一路随机产生的一个高斯白噪声信号作为背景噪声源，可以更好地模拟轴承运转的噪声环境。

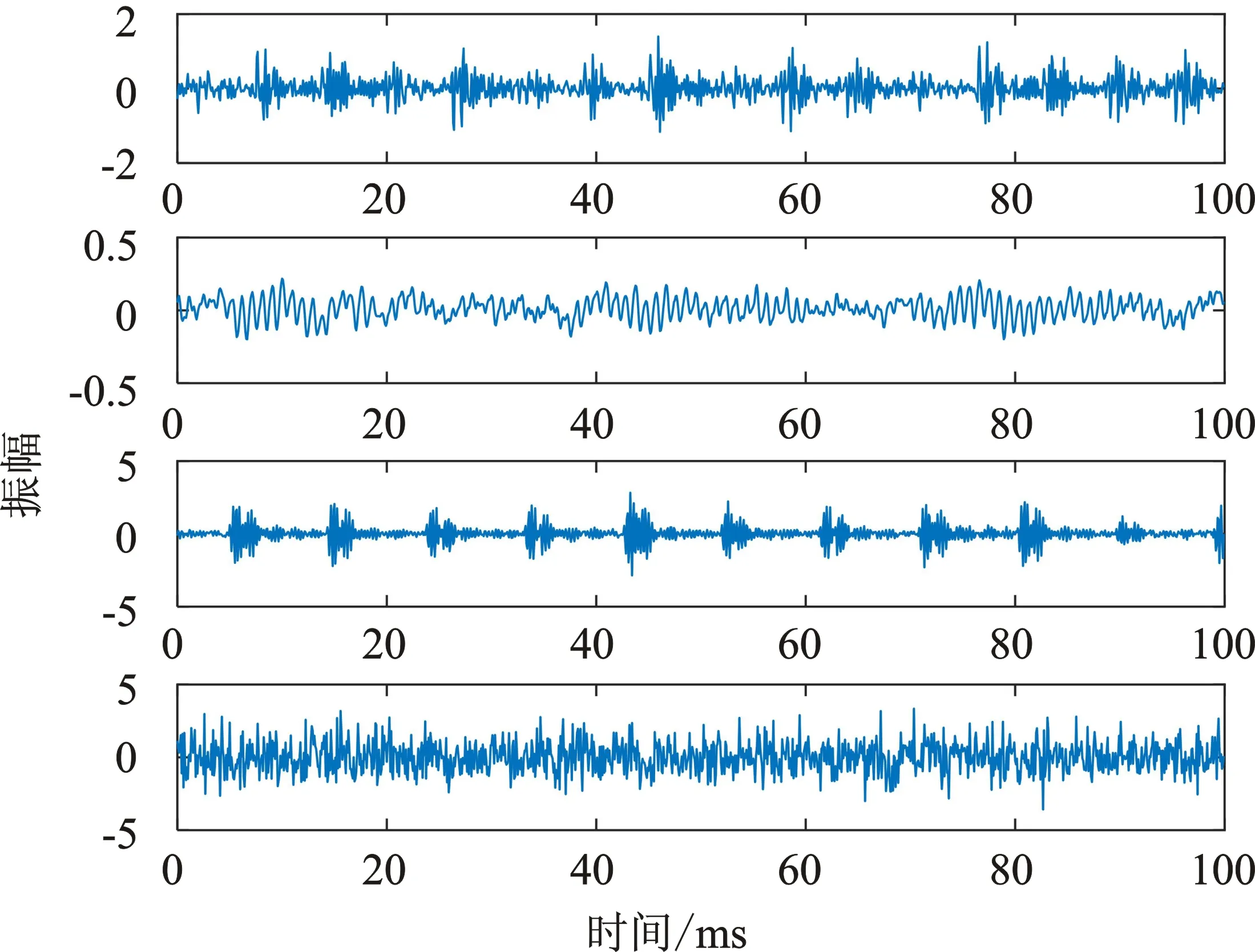
(a) 时域波形

从图3(b)中可以看出，源信号中内圈故障特征频率为159.7 Hz，外圈故障特征频率为106.2 Hz，且能看到其对应的故障特征频率的倍频。倍频的存在是由于轴承实际安装过程中存在不对中的情况，不对中越严重，则倍频成分在振动信号中表现越明显。首先通过随机生成的混合矩阵对源信号进行混合，分别提取混合信号中的内圈故障特征信号和外圈故障特征信号，再将提取后的故障特征信号作为循环维纳滤波器的期望信号，最后对混合信号进行循环维纳滤波，得到提取到的单一故障源信号。

选取混合信号中通道1的信号作为循环维纳滤波的输入信号。该通道混合信号的包络谱如图4(a)所示。从包络谱中可以看到混合信号中包含频率为106.2 Hz的外圈故障特征频率成分和频率为159.7 Hz的内圈故障特征频率成分。采用现有方法提取输入信号中的内圈故障源信号，其中采用典型循环维纳滤波方法[20]提取结果的包络谱如图4(b)所示，从图中可以看到频率为159.3 Hz的内圈故障特征频率成分，但同时也可以看到频率为105.5 Hz的外圈故障特征频率成分和频率为16.11 Hz的干扰成分，对比输入信号，典型循环维纳滤波方法没有将内圈故障源信号从混合信号中提取出来，因此典型循环维纳滤波方法不适用于轴承复合故障诊断。采用人工合成循环维纳滤波方法[22]提取结果的包络谱如图4(c)所示。从包络谱中可以看到该方法能够从混合信号中提取出频率成分为164.8 Hz的内圈故障特征频率成分，但根据图4(a)，在输入的混合信号中内圈故障特征频率应为159.7 Hz，与人工合成循环维纳滤波方法提取结果不同，这是因为轴承在不同载荷下工作时产生的游隙不同，从而使实际接触角与标称接触角存在一定误差，而人工合成信号依赖于标称参数，所以人工合成信号与实际信号故障频率存在误差；采用人工合成循环维纳滤波方法也不能从混合信号中提取出实际的故障源信号。

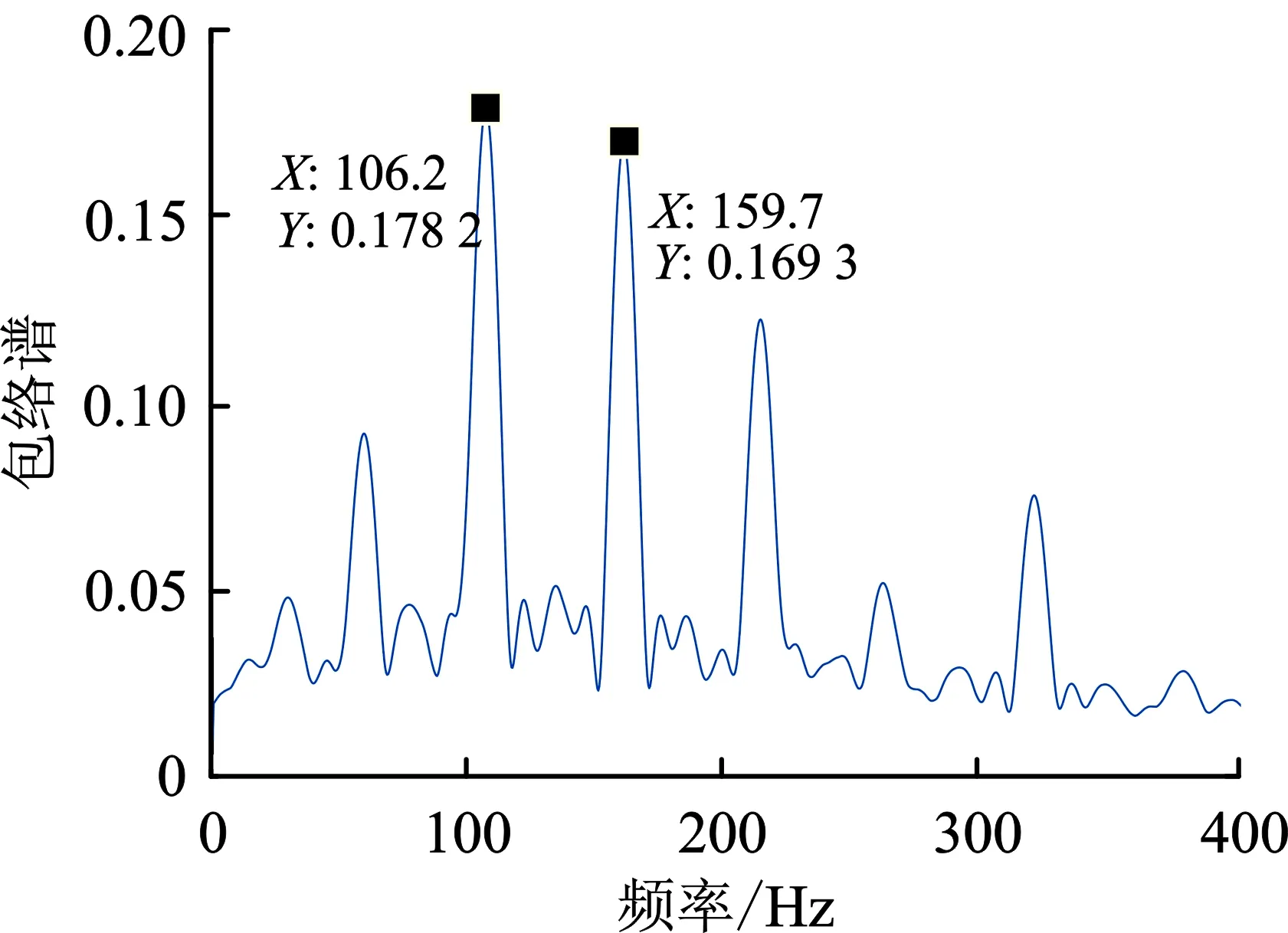
(a) 混合信号包络谱

采用笔者提出的基于CCA盲提取的循环维纳滤波提取混合信号中的内圈故障源信号。图5(a)为CCA提取过程中代价函数收敛曲线。图中虚线代表最优解对应的代价函数值，实线表示自适应迭代中代价函数的收敛曲线。从曲线中可以看到算法的收敛速度较快，可以在2 000次迭代内达到收敛；将CCA盲提取得到的故障特征信号作为循环维纳滤波的期望信号，对混合信号进行滤波。图5(b)为循环维纳滤波结果的包络谱。从包络谱中可以看到频率成分为159.7 Hz的内圈故障特征频率成分及其倍频，同时外圈故障特征频率成分被抑制，验证了笔者提出的基于CCA盲提取的循环维纳滤波可以从混合信号中提取出内圈故障源信号。

(a) 代价函数收敛曲线

上述仿真证明了在提取内圈故障源信号时，笔者提出的方法提取效果优于现有的典型循环维纳滤波方法和人工合成循环维纳滤波方法的提取效果，接下来采用现有方法从混合信号中通道1的信号中提取外圈故障源信号，提取结果如图6所示。

(a) 典型循环维纳滤波方法提取结果

图6(a)为典型循环维纳滤波方法提取结果的包络谱。从图中可以看到频率为106.2 Hz的外圈故障特征频率成分、频率为159.7 Hz的内圈故障特征频率成分以及频率为58.96Hz的干扰成分，这说明采用混合信号直接作为期望信号不能从混合信号中提取外圈故障源信号，因此不适用于轴承复合故障诊断。图6(b)为采用人工合成循环维纳滤波方法提取外圈故障源信号结果包络谱，可以看出输出信号中包含了频率为108 Hz的外圈故障特征频率，与实际混合信号中频率为106.2 Hz的外圈故障特征频率存在一定误差，因此也不适用于轴承复合故障诊断问题。

采用CCA盲提取得到的外圈故障特征信号作为期望信号，从混合信号中提取外圈故障源信号的提取结果如图7所示。

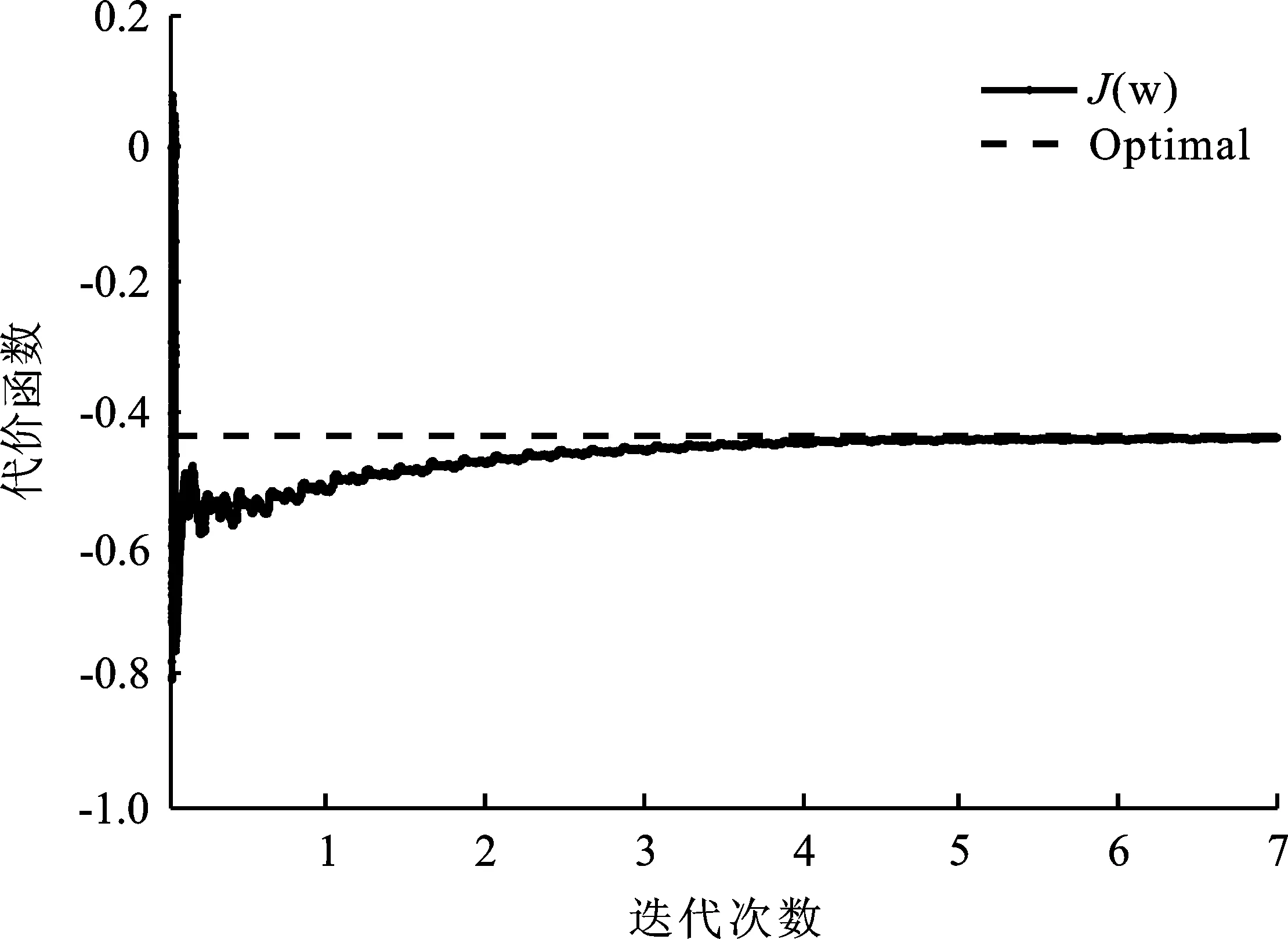
(a) 代价函数收敛曲线

图7(a)为CCA盲提取过程中代价函数收敛曲线。图中虚线代表最优解对应的代价函数值，实线表示实际自适应迭代中代价函数的收敛曲线。可以看到算法可以收敛到外圈故障信号提取向量的最优解。将CCA盲提取得到的故障特征信号作为循环维纳滤波器的期望信号，对混合信号进行滤波。图7(b)为提取得到的外圈故障源信号的包络谱。从包络谱中可以看到频率为106.2 Hz的外圈故障特征频率成分及其倍频，同时频率为159.7 Hz的内圈故障特征频率成分被抑制。仿真实验表明，文中提出的方法可以从混合信号中提取单一故障源信号，且提取效果优于现有典型循环维纳滤波方法和人工合成循环维纳滤波方法。

4.2 实验结果

为了验证算法的实际处理效果，在航发主轴轴承试验机上采集了具有复合故障的轴承振动信号。试验轴承是型号为D276126NQ1U的双半内圈三点接触球轴承，轴承尺寸参数如表1所示。该轴承是航空发动机中支撑高压压气机的前支点止推轴承，主要承受轴向和径向的交变载荷，工作环境恶劣，容易发生故障。

表1 轴承尺寸参数

试验轴承是某型航空发动机例行检修过程中拆卸的废旧轴承，在轴承的内圈和外圈滚道上均发现有轻微点蚀故障，是典型的复合故障轴承。振动信号采集过程中主轴转速为1 000 r/min，振动信号采样率为20 kHz。根据式(7)和(8)计算得到轴承故障特征频率，其中，内圈故障特征频率为159.9 Hz，外圈故障特征频率为123.4 Hz。实验中使用8个加速度传感器来采集8个通道的轴承振动加速度信号，其中，在轴承座上布置了3个加速度传感器，在试验机外壳上布置了5个加速度传感器，传感器具体布置位置如图8所示，其中传感器AC0采集到的轴承振动信号成为通道0观测信号。在实际工况下，传感器采集到的振动信号往往是各个振源振动的综合反映，且各部件到传感器的传递路径和衰减情况也是未知的。直接利用采集的信号进行故障分析和故障源识别往往是不可靠的，因此采用笔者提出的循环维纳滤波对观测信号进行滤波处理，得到的故障源信号可以有效抑制混合信号中的干扰信号，为后续故障分析与分类识别提供了更加可靠的信息。

(a) 试验机外壳上传感器布置

为了更好地衡量特定信号的滤波效果，定义信号干扰比(Signal to Interference Ratio，SIR)如下：

(23)

其中，rs为目标故障特征频率成分的幅值，ri为除去目标故障特征频率成分及其倍频分量后的最大干扰特征频率成分的幅值。例如在滤波器期望输出为内圈故障源信号时，由于内圈故障和外圈故障为本实验中两个主要振动源，因此最大干扰为外圈故障源信号。类似地，在提取外圈故障源信号时，最大干扰为内圈故障源信号。信干比越大，说明循环维纳滤波的滤波效果越好，对干扰成分的抑制越充分。为了更好地说明本文提出的CCA循环维纳滤波方法的故障诊断效果，将文中方法的诊断效果与典型循环维纳滤波方法[20]和人工合成循环维纳滤波方法[22]的诊断效果进行了对比分析。

对通道2采集到的混合振动信号做包络谱分析，结果如图9(a)所示。从图中可以分析得到混合信号中包含频率为17.09 Hz的转频信号，频率为124.5 Hz的外圈故障源信号，频率为159.9 Hz的内圈故障源信号。采用典型循环维纳滤波方法对混合信号进行滤波，滤波后信号的包络谱如图7(b)所示。从包络谱中可以看到，典型循环维纳滤波方法的信号干扰比为1.36，该方法不能从混合信号中较为清晰地提取出内圈故障源信号，这是因为典型循环维纳滤波方法所采用的期望信号为混合信号本身；这种方法对单一故障的滚动轴承振动信号的滤波效果较好，但却不适用于滚动轴承的复合故障诊断问题。

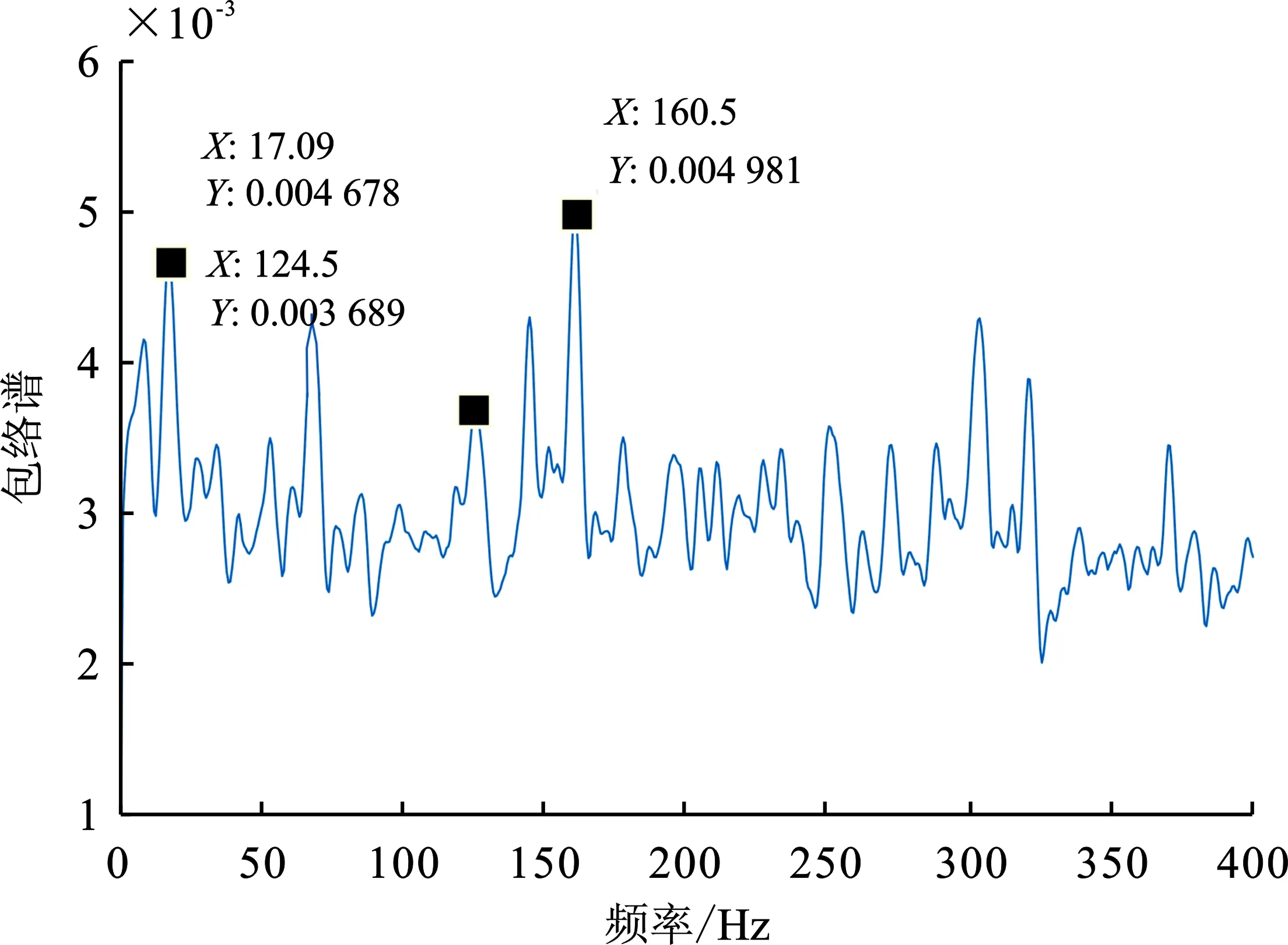
(a) 观测信号(通道2)

人工合成循环维纳滤波方法采用人工合成的单一故障特征信号作为循环维纳滤波的期望信号，滤波后信号的包络谱如图10所示。

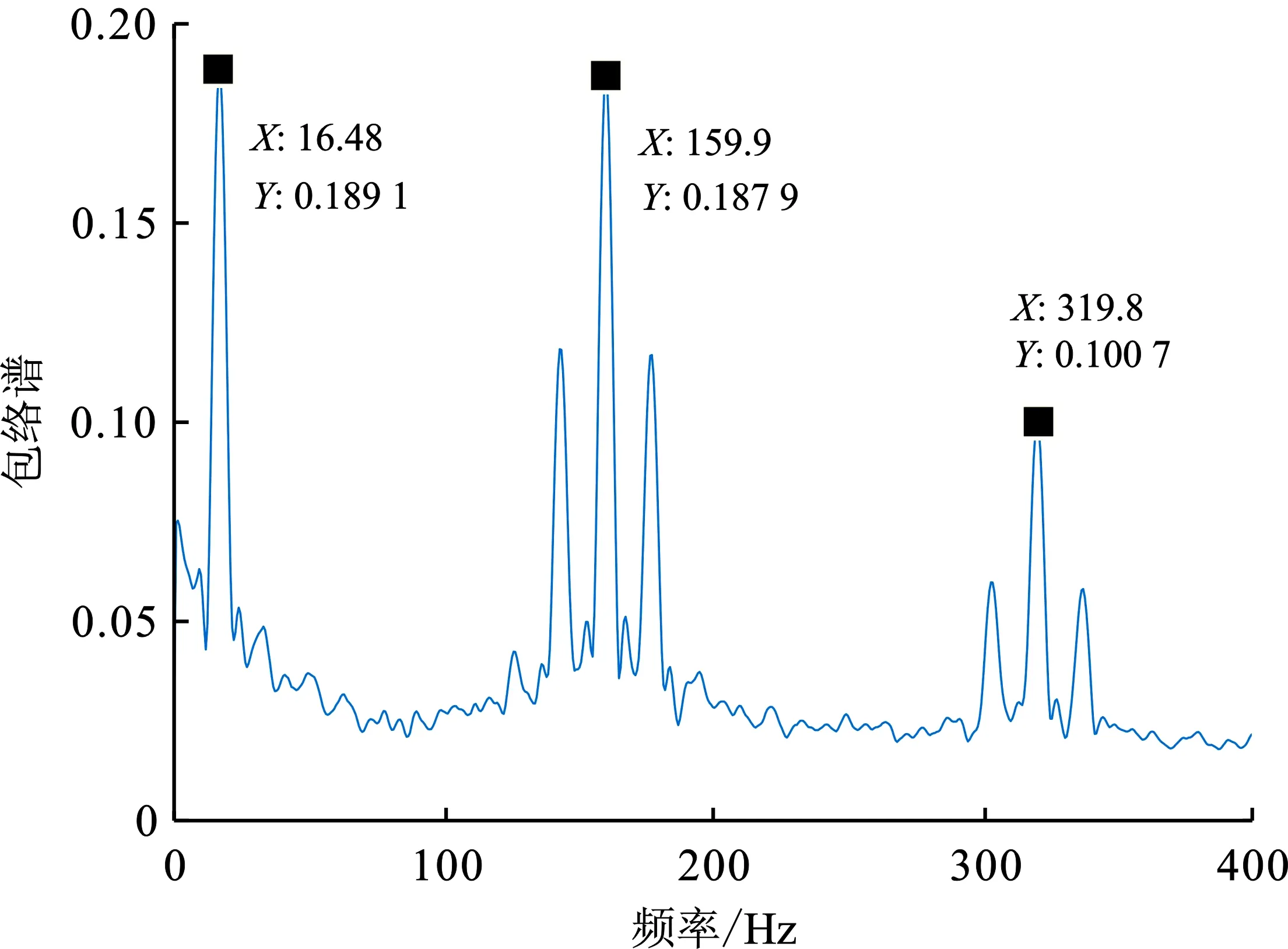
(a) 人工合成循环维纳滤波方法(参数1)滤波结果

表2 方法2所用参数

人工合成循环维纳滤波方法的缺点在于过于依赖人工合成振动信号中的参数，例如轴承转速及接触角，在轴承的实际工作中，这些参数往往不是固定不变的，因此很难得到这些参数准确的先验信息。采用表2中所示的两组不同的参数合成不同的振动信号，将合成的信号分别作为循环维纳滤波的期望信号，采用第一组参数滤波后信号的包络谱如图10(a)所示，采用第二组参数滤波后信号的包络谱如图10(b)所示。从图10(a)中的包络谱中可以看到滤波器提取了频率为159.9 Hz的故障源信号，从图8(b)中的包络谱中可以看到滤波器提取了频率为177 Hz的故障源信号，但从图9(a)中的包络谱中可以看到采集到的混合信号中内圈故障频率为159.9 Hz，因此人工合成循环维纳滤波方法不能真正地从混合信号中提取出目标故障源信号。

采用笔者提出的基于CCA盲提取的循环维纳滤波方法对混合信号进行滤波，结果如图11所示，从包络谱中可以看到，笔者提出的方法可以将特征频率为159.9Hz的内圈故障源信号提取出来，同时其它干扰分量也被明显抑制，信号干扰比为3.07。

通道0采集到的混合振动信号做包络谱分析结果如图12(a)所示。从图中可以看到混合信号中包含频率为17.09 Hz的转频信号，频率为124.5 Hz的外圈故障源信号，频率为159.9 Hz的内圈故障源信号，且外圈故障源信号的幅度较小，内圈故障源信号的幅度较大，因此提取外圈故障源信号的难度更大。采用典型循环维纳滤波方法对混合信号进行滤波，滤波后信号的包络谱如图12(b)所示。从包络谱中可以看到，提取结果信号干扰比为0.39，这说明典型循环维纳滤波方法不能从混合信号中提取出外圈故障源信号。

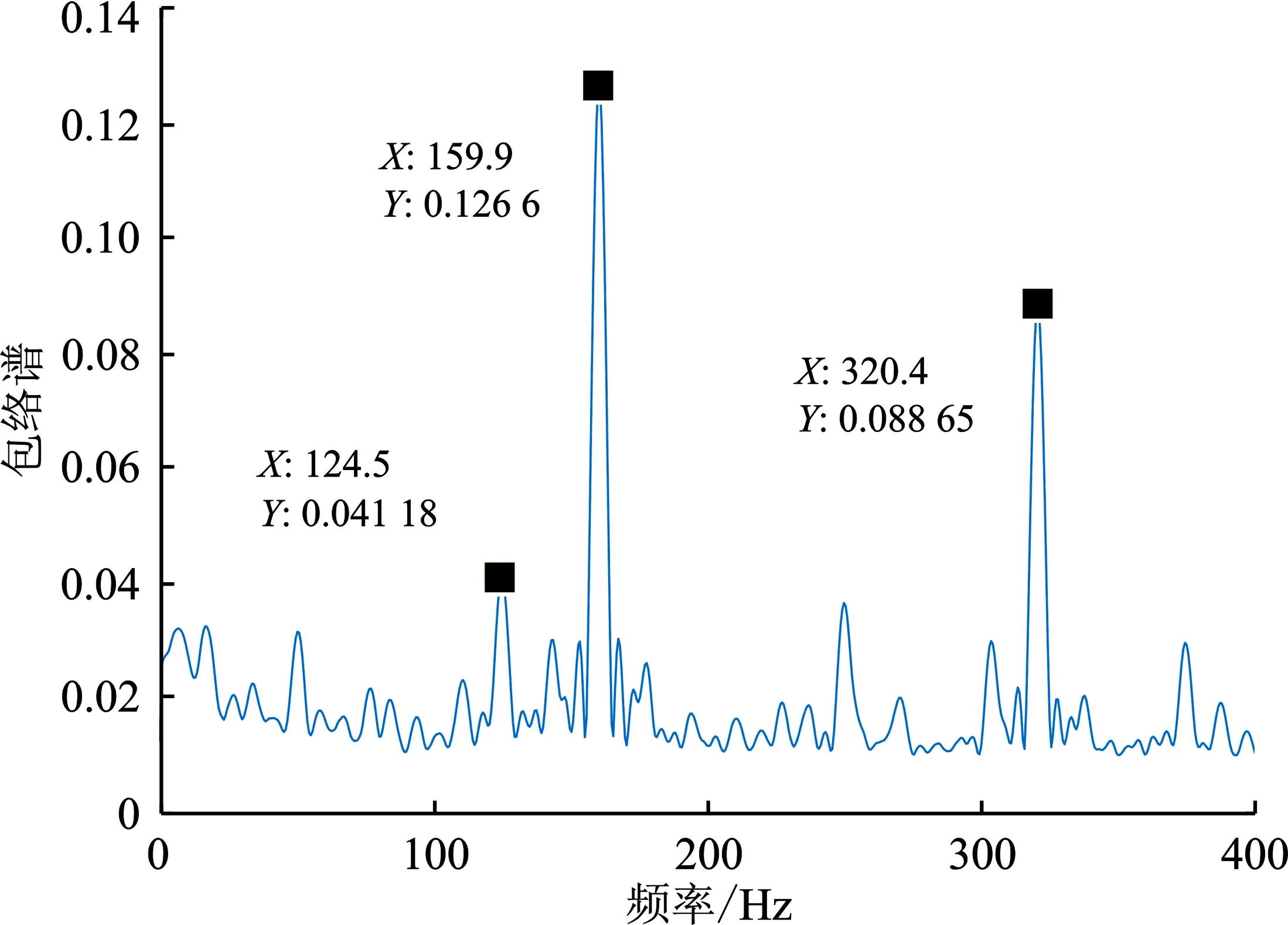
图11 内圈故障源信号提取结果

(a) 观测信号(通道0

人工合成循环维纳滤波后的信号包络谱如图13所示，其中人工合成信号中采用的参数如表2所示，将合成的信号分别作为循环维纳滤波的期望信号，采用第一组参数滤波后信号的包络谱如图13 (a)所示，采用第二组参数滤波后信号的包络谱如图13(b)所示。从图13(a)中的包络谱中可以看到滤波器提取了频率为123.3 Hz的故障源信号，从图13 (b)中的包络谱中可以看到提取了频率为136.1 Hz的故障源信号，但从图12(a)中的包络谱中可以看到采集到的混合信号中外圈故障特征频率为124.5 Hz，因此采用人工合成循环维纳滤波得到的结果并不可信，不能真正地从混合信号中提取出目标故障源信号。

(a) 人工合成循环维纳滤波(参数1)滤波结果 (b) 人工合成循环维纳滤波(参数2)滤波结果

采用CCA盲提取得到的外圈故障特征信号作为循环维纳滤波的期望信号，提取得到的外圈故障源信号包络谱如图14所示，从包络谱中可以看到，笔者提出的方法可以将特征频率为124.5 Hz的外圈故障源信号提取出来，同时内圈故障特征信号也被明显抑制，信号干扰比为2.51。

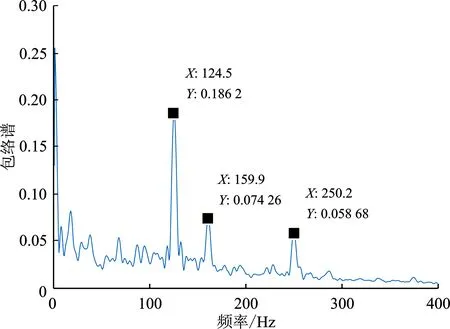
图14 外圈故障源信号提取结果

5 结束语

笔者提出了一种航发主轴轴承复合故障诊断的循环维纳滤波方法。虽然部分文献中已使用循环维纳滤波对轴承故障进行诊断，但得到的算法依赖于轴承的先验知识，在实际应用中这些先验知识难以获取，且可能随着轴承运行状态的不同而时时改变，因此这些算法并不适用于航发主轴轴承复合故障诊断。笔者提出的算法克服了这些缺点，首先对混合信号进行基于共轭梯度优化算法的CCA盲提取，将提取到的故障特征信号作为循环维纳滤波的期望信号，再根据待提取信号的循环平稳特性得到循环频率，最后对混合信号进行滤波得到单一故障源信号，结合对其包络谱的分析完成对航发主轴轴承的复合故障诊断。通过大量的仿真与航发主轴轴承复合故障诊断实验结果验证了笔者提出的方法对复合故障诊断的有效性，同时，证明了与现有的典型循环维纳滤波方法和人工合成循环维纳滤波方法相比，采用笔者提出的方法得到的故障源信号的信噪比更高。