5G卫星通信系统频偏估计算法*

王中旗，崔高峰，王卫东，李秀华

(北京邮电大学 电子工程学院，北京 100876)

0 引 言

随着卫星带宽成本的下降和卫星通信技术的进步，在高通量卫星带宽巨大需求的刺激下，国内外掀起了卫星通信发展的热潮，卫星通信进入到一个新的发展阶段。5G要实现万物互联的愿景，卫星通信是其中重要一环。地面 5G 移动通信系统与低轨卫星移动通信系统相融合[1]，可以充分发挥两者的优点，构成全球无缝覆盖和无缝切换的通信网络，从而满足全域覆盖的通信服务要求。3GPP和ITU等标准化组织在积极推动5G融合卫星移动通信的研究工作，先后在多份研究报告中涉及5G卫星通信有关的研究内容。文献[2]定义了在5G中使用卫星接入的三大类别，分别是连续服务、泛在服务和扩展服务。借助卫星通信无视地形地貌和距离的无死角广域覆盖能力，卫星通信与5G相互融合，共同构成全球无缝覆盖的海、陆、空、天一体化综合通信网，满足用户无处不在的多种业务需求，是未来通信发展的重要方向。

为能够高速传输数据，在5G通信系统中，下行传输采用正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)波形[3]。OFDM技术能够抑制符号间干扰，频谱利用率高，具有很强的抗衰落能力。然而OFDM技术对频率偏差非常敏感，频率偏差会破坏子载波间的正交性，产生严重的载波间干扰(Inter-carrier Interference，ICI)和码间干扰(Inter-symbol Interference，ISI)，导致信号无法准确地解调出来，降低系统的性能。卫星移动通信环境和地面无线信道具有显著的差异，卫星和移动终端之间的高速相对运动产生大的多普勒频移[4]，有时大于几个子载波间隔。如何在这种场景中利用5G标准定义的同步序列实现精准的频率同步，是5G空口信号与卫星通信融合的关键问题之一。

基于OFDM系统的多普勒频移估计算法在过去得到了广泛的研究。通常将大的多普勒频偏分为小数倍频偏(Fractional Frequency Offset，FFO)和整数倍频偏(Integer Frequency Offset，IFO)两部分分别进行估计[5]。根据算法所利用数据类型的不同，可以划分为盲估计算法和数据辅助型估计算法，通常盲估计算法的估计精度不及数据辅助型估计算法。在现有的地面移动通信系统中，例如长期演进系统(Long Term Evolution，LTE)和5G，都定义了特殊的主同步序列(Primary Synchronization Signal，PSS)，通过互相关算法进行频率同步。文献[6-8]提出了使用循环前缀(Cyclic Prefix，CP)和PSS通过最大似然(Maximum Likelihood，ML)算法与互相关算法估计FFO，算法复杂度较高。这些算法大多都是针对移动性相对较低的地面无线信道而设计的，在存在较大多普勒频偏的低轨卫星系统中应用时，其性能可能会下降。

本文针对卫星移动通信系统星地链路中存在的大多普勒频偏问题，以及同时存在的终端与卫星侧晶振误差引起的载波频偏问题，对5G空口信号在星地链路中的适用性展开研究，重点探索大多普勒频移场景下的频率同步技术，解决大频偏环境下的频率同步问题——这是5G与卫星通信融合的关键问题之一。

1 5G NR下行物理层

1.1 帧结构

5G帧结构是在LTE标准基础上进行设计的。根据协议38.211，5G上下行链路一个无线帧(Radio Frame)的时长固定为10 ms，由10个子帧(Subframe)组成，编号为0～9，每个子帧的长度固定为1 ms，如图1所示。

图1 5G帧结构

表1 5G NR帧结构参数

fscs=2μ·15，当μ=2时，子载波间隔fscs=60 kHz，可以支持常规和扩展循环前缀两种类型，其他的只支持常规循环前缀。

1.2 同步信号

m序列具有极好的自相关特性、较好的互相关特性和抗频偏特性。5G系统中定义PSS为长度为127经过BPSK调制的m序列，在频域上被映射到连续的127个子载波。主同步信号dPSS(n)定义为

(1)

式中：序列x(m)定义为

x(i+7)=(x(i+4)+x(i))mod 2×

[x(6)x(5)x(4)x(3)x(2)x(1)x(0)]=

[1 1 1 0 1 1 0] 。

(2)

在资源网格中，PSS、辅同步序列(Secondary Synchronization Signal，SSS)和物理广播信 道(Physical BroadcastChannel，PBCH)组成一个同步信号资源块(Synchronization Signals Blocks，SSB)传输。在时域中，1个SSB包含4个OFDM符号(编号0～3，用l表示)；在频域中，1个SSB包含240个连续的子载波(编号0～239，用k表示)。PSS、SSS和PBCH在SSB中的资源映射情况如图2所示，纵向表示频域，横向表示时域。

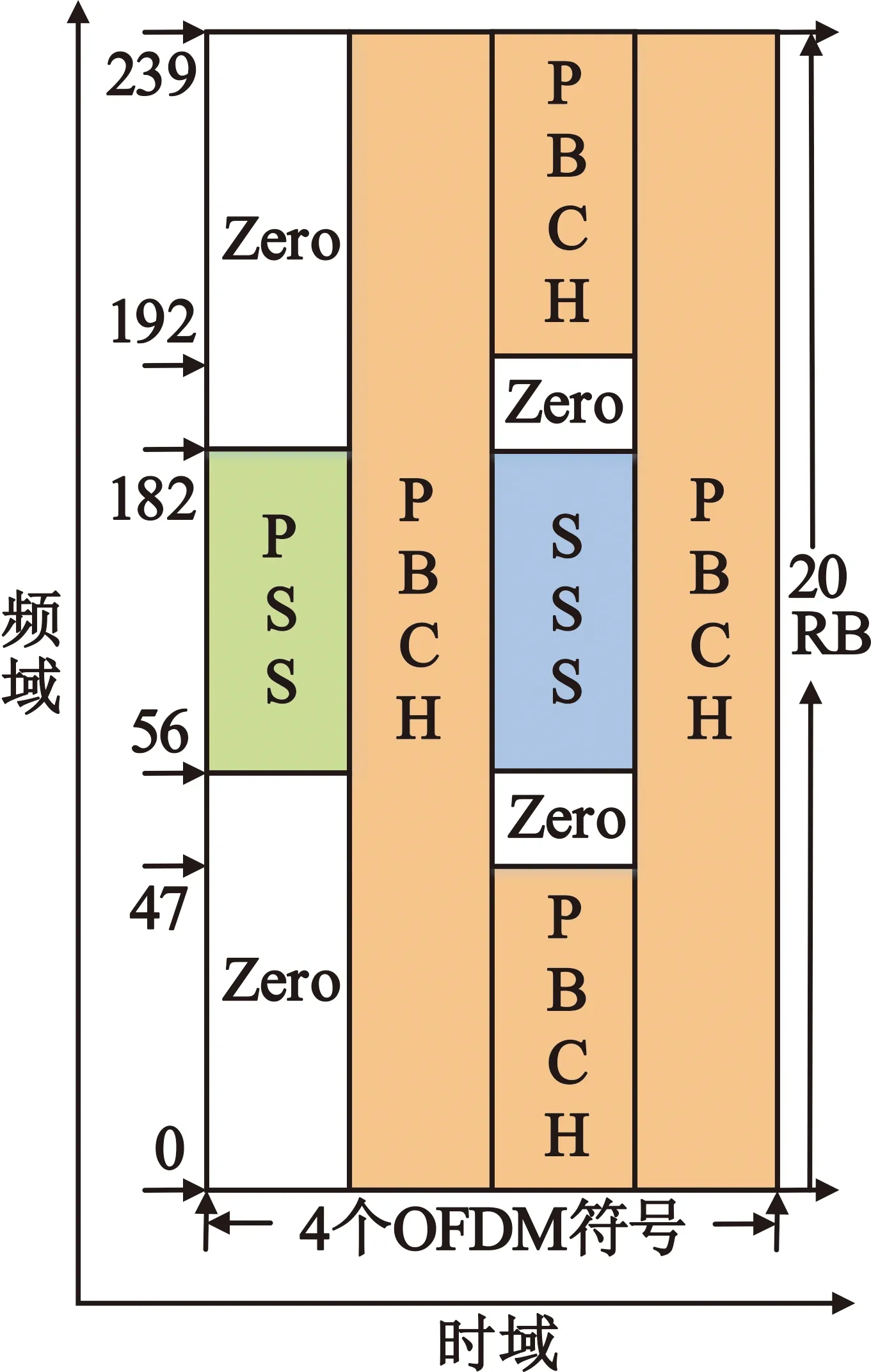
图2 SSB结构示意图

从图2中可以看出，时域上，PSS和SSS分别位于第一个和第三个OFDM符号，相对位置固定；频域上，PSS和SSS均占用SSB中央位置的127个子载波，PSS前后分别有56个和57个子载波置零，SSS前后分别有8个和9个子载波置零。

一般来说，导频符号对于移动通信系统中的快速载波同步是必要的。在卫星通信系统中，大的频偏和极低的信噪比是OFDM在实际应用中面临的两大挑战[10]。因此，本文主要考虑采用5G帧结构的PSS进行载波同步。

2 频偏估计算法分析与改进

2.1 信号模型

时域离散基带OFDM符号传输s(n)可表示为

(3)

式中：Xk表示第k个子载波上的已调数据，N表示快速傅里叶变换(Fast Fourier Transform,FFT)的长度。考虑发射机和接收机之间的多普勒频偏和振荡器的不匹配以及加性高斯白噪声(Additive White Gaussian Noise，AWGN)的情况下发送s(n)，在模数(A/D)转换后，接收机处一个OFDM符号的离散信号由以下公式给出：

r(n)=s(n)ej2πεn/N+ω(n)。

(4)

式中：ε表示相对于子载波间隔归一化的频率偏移，可分为两部分，整数倍频偏εi和小数倍频偏εf；ω(n)表示白噪声。

2.2 基于PSS的互相关算法

首先，通过计算两个符号在一定间隔内的相位差来估计小数倍频偏。在粗定时同步的最优时刻，不考虑信道多径和噪声的条件下，假设接收到的时域m序列为

(5)

式中：εf表示归一化的小数倍频偏，s(k)表示发送端的时域m序列。用r(k)和s(k)逐点做相关，得到一个新的相关序列，记为x(k)，即

(6)

接收到的PSS信号与本地保存发送端的PSS信号共轭相乘本质上是为了消除接收信号的相位，只留下由于频偏带来的附加相位，那么x(k)的前半段的数据和后半段对应的数据会有一个频偏引起的固定的相位差。将x(k)均分为前后两段，再次相关得到

(7)

上式可估计的归一化小数倍频偏为

(8)

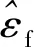
(9)

整数倍频偏εi根据接收的频域PSS和本地保存发送端的频域PSS互相关值最大一组对应的循环移位值确定。对接收PSS序列rc(k)做FFT变换得到频域序列Rc(n)，S(n)表示本地保存的发送的频域PSS序列，因此估计整数倍频偏的相关函数可以定义为

(10)

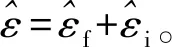
2.3 基于PSS的插值与互相关算法

本文提出一种对接收PSS进行插值，增加采样点数，再利用传统基于PSS互相关的算法估计小数倍频偏的方法，实现过程如图3所示。

图3 本文所提算法实现结构

插值会增加计算量和硬件实现的复杂度，级联积分梳状(Cascade Integrator Comb,CIC)滤波器的实现简单且速度高，仅仅利用加法器、减法器和寄存器，没有乘法运算，节约了硬件资源，经常被运用在插值运算单元中。本文将运用CIC滤波器对PSS进行插值。下面简单介绍CIC滤波器的基本组成原理[11]。

CIC滤波器的冲激响应为

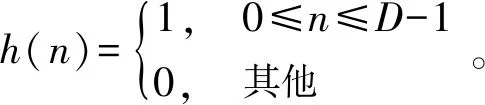
(11)

式中:D为CIC滤波器的阶数，其Z变换为

(12)

其分母一个积分器，分子是一个梳状滤波器。单级CIC滤波器基本结构如图4所示。

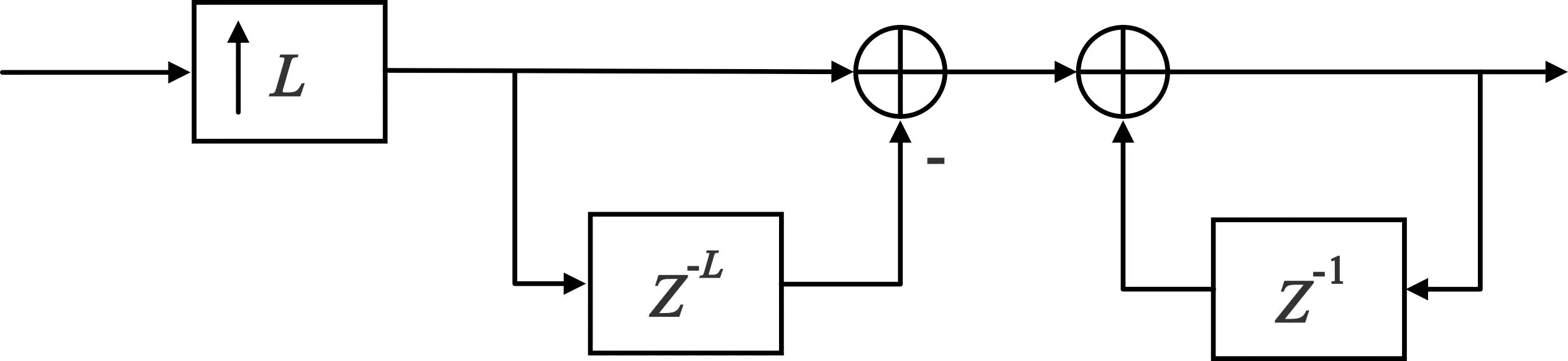
图4 单级CIC滤波器的原理结构

图4中L表示插值倍数。单级CIC滤波器的第一旁瓣电平较大，且与滤波器的阶数无关。这个值不满足通常的阻带衰减要求，解决方法是通过级联CIC滤波器来达到更大的阻带衰减，但是级联数量一般不能超过5，在本设计中采用3级级联的方式，如图5所示。根据Noble恒等式(“先进行抽取或者插值，再进行线性滤波”与“先进行线性滤波，再进行抽取或者插值”这两者是可以等价的),可以将多级CIC滤波器结构变换为工程中实际应用的Hogenauer CIC滤波器结构。

图5 3级Hogenauer CIC内插滤波器结构

经过变换得到的Hogenauer CIC滤波器的积分部分与滤波部分分别工作在高速区与低速区，与直接将多个单级CIC滤波器级联相比，使得 CIC滤波器更容易实现，效率大大增加。

插值器可将数据采样点从N增大到L·N。传统的插值方法是在相邻两个采样点之间等间隔地插入L-1个0值点，本文则是根据采样定理，提高采样率，增加采样点数，在相邻两个采样点a与b之间等间距地插入L-1个采样点。假设点a的值为y1，b的值为y2，则在采样点a与b之间插入的值如下式所示：

(13)

3 算法仿真与性能分析

为了验证本文改进的基于PSS的插值与互相关算法的性能，本节将利用Matlab进行仿真分析。

3GPP对于结合了 5G 的卫星信道考虑了开放环境、乡村、郊区、城市和密集城市这些用户场景，通过采用的频段来区分所处的环境。在开放环境中，一般采用 AWGN信道。对信道建模中，频段支持频率范围0.5～100 GHz，特别针对低于6 GHz的频段和Ka频段两个频段。对于Ka频段内的通信，卫星移动通信系统中多普勒频偏值的变化范围为±750 kHz[12]，所以本文加的归一化频偏大小为±50.5。具体仿真参数如表2所示。

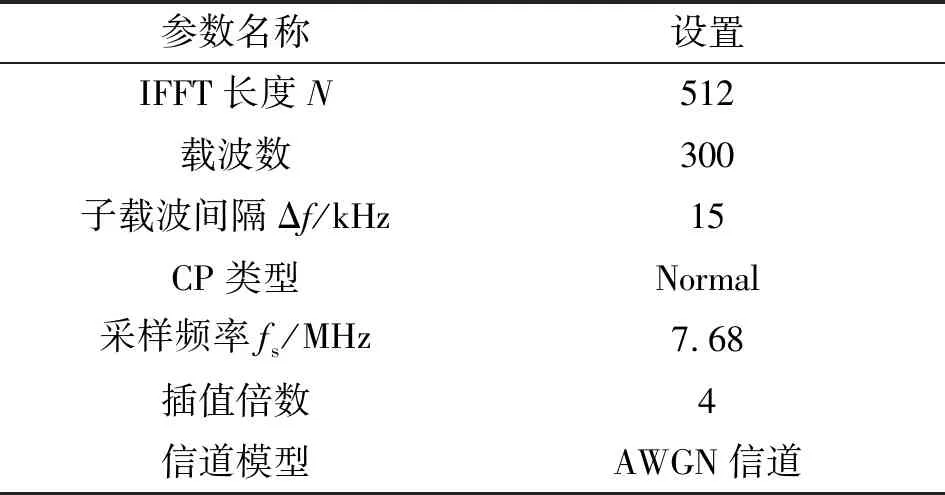
表2 仿真参数表

图6和图7分别给出了对PSS实部和虚部数据插值的结果，可以看出插值后的波形与插值前相同，插值前的采样点完全在插值后的采样点上，插值后的波形只是在每2个采样点之间插入了3个点，将512采样点的PSS经4倍的插值到2 048点。

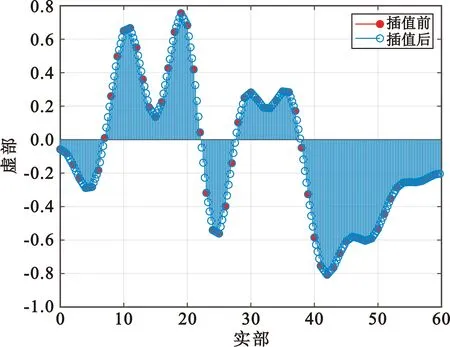
图6 实部数据插值结果

图7 虚部数据插值结果

图8仿真对比了本文提出的基于PSS插值与互相关算法、基于PSS的互相关算法和基于CP的算法均方误差(Mean Squared Error，MSE)性能。仿真结果显示，随着信噪比(Signal-to-Noise Ratio，SNR)的增加，MSE都会下降，但本文提出的算法性能比基于CP的算法有大幅的提高，同时优于基于PSS的互相关算法。

图8 三种算法的MSE性能

图9仿真对比了本文提出的基于PSS插值与互相关算法、基于CP的算法和基于PSS的互相关算法在5G卫星通信系统链路大频偏情况下误码率(Bit Error Rate，BER)性能。仿真结果表明，在SNR<8 dB时，本文提出的算法具有良好的性能；当SNR>8 dB时，本文提出的算法明显优于另外两种算法，误码率达到10-6，可以应用于低信噪比的传输环境。本文的算法主要分为两步，第一步内插因为利用CIC滤波器进行，没有乘法，只涉及到少量的加减运算，所以该算法的运算量主要体现在第二步数据相关运算过程中。因为数据由N点增加到4N点，所以增加了3N次乘法、3N次加法，乘法运算没有大幅增加，运算速度不会有太大降低，资源占用量不会有增加，因此算法具有较强的实用性。

图9 三种算法的BER性能

4 结 论

本文针对卫星移动通信系统星地链路中存在的大多普勒频偏问题，以及同时存在的终端与卫星侧晶振误差引起的载波频偏问题，对5G空口信号在星地链路中的适用性展开研究，提出了使用5G下行同步信号的频偏估计算法。通过对基于PSS互相关的频偏估计算法的分析，提出对PSS先使用CIC滤波器插值增加采样点再利用基于PSS互相关的频偏估计算法估计小数倍频偏的方法。对所提算法的仿真结果表明，在AWGN信道，频偏较大的情况下，改进算法比传统算法在低信噪比下具有更好的性能，能够在5G卫星移动通信系统中实现准确的频偏估计和正确的频偏补偿。虽然插值会增加计算过程，但使用CIC滤波器易于实现，计算量不大，有较强的实际应用价值。