多层滑带滑坡抗滑桩桩后推力分布计算方法研究*
2022-02-11胡新丽张杰豪
胡新丽 徐 楚 张杰豪
(中国地质大学(武汉)工程学院, 武汉 430074, 中国)
0 引 言
多层滑带滑坡是一种危害非常严重并且分布广泛的自然地质灾害,严重影响着我国人民的生命财产安全(李守定等, 2004; 黄润秋, 2007; 任伟中等, 2009; 代贞伟等, 2016; 向家松等, 2017; Wang et al.,2018; Zhang et al.,2018; Tang et al.,2019; 郭长宝等, 2022; Xu et al.,2022; 朱鸿鹄等, 2022)。抗滑桩是目前开展滑坡治理使用最为广泛的防治结构之一,在我国滑坡地质灾害治理中广泛应用(胡新丽等, 2005; 李长冬, 2009; 李新哲等, 2021)。在进行抗滑桩设计时,需要确定滑坡推力的大小和分布(Ke et al.,2006; Powrie et al.,2007; 戴自航等, 2007; Zhang et al.,2015; Ke et al.,2019; Xiong et al.,2019; Yan et al.,2020)。多层滑带滑坡演化过程具有多级滑体相对运动、应力非连续性特点,滑坡推力分布和单层滑带滑坡不同,亟需对多层滑带滑坡推力计算方法进行深入研究。
目前国内外研究学者主要通过理论计算和模型试验等方法确定滑坡的推力分布形式,已经取得了较多研究成果。戴自航(2002)通过理论推导和试验分析将滑坡推力分布模式分为三角形、梯形和矩形3种; 杨涛等(2006)通过假设圆弧组合面,使用Janbu法计算滑坡推力; 肖世国(2010)对似土质滑坡进行了水平微段极限平衡法的分析,推导出了滑坡推力的计算公式; 郑宏(2007)和凌道盛等(2013)采用迭代的方法对三维滑坡稳定性和滑坡推力进行了研究; Sharafi et al. (2016)通过模型试验和数值模拟研究了坡顶加载条件下,不同因素对抗滑桩桩后推力分布的影响; 陈鑫等(2019)基于土拱效应解释了滑坡推力呈“中间大、两头小”抛物线分布规律的原因; 蔡强等(2016)通过模型试验表明钢管抗滑短桩桩后滑坡推力呈现“S”型分布; Zhang et al. (2018)基于有限差分方法并考虑不同力学参数的影响,研究了含多滑带的滑坡推力分布形式。这些研究成果在一定程度上解决了实际工程中滑坡推力计算的问题,但滑坡推力分布模式只有三角形、矩形、梯形或抛物线形等形式,而且不适用于多层滑带滑坡。
综上所述,国内外研究学者对抗滑桩桩后推力进行了深入研究,但对多层滑带滑坡推力分布的相关研究还刚刚起步。单层滑带滑坡和多层滑带滑坡的滑坡推力在水平方向上的分布特征相似,在竖直方向上分布特征有所区别。相关学者一般认为竖直方向上的滑坡推力的分布图式为三角形、矩形、梯形或者抛物线形。由于不同层滑体间的相对运动,多层滑带滑坡-抗滑桩所受滑坡推力分布规律和单层滑坡-抗滑桩所受滑坡推力分布有所区别,目前缺少对于多层滑带滑坡抗滑桩桩后推力分布的研究。本文通过改进水平极限平衡法,考虑了滑带处的受力传递,提出了多层滑带滑坡抗滑桩桩后推力分布计算方法,并通过数值模拟进行了工程案例验算分析,为多层滑带滑坡的防治理论提供了一定的参考。
1 理论模型
建立如图 1所示的理论分析模型,抗滑桩后侧滑体沿滑面滑移达到极限平衡状态,z为沿桩侧的计算深度,方向竖直向下。自桩顶起向下沿着z轴方向取微段dz,进行隔离体受力分析。
为了便于分析问题,该计算模型采用如下假定:(1)在同一层滑体内,该微段的上下表面的剪应力大小τ相等,根据肖世国(2010)的验证,τ可按库仑摩擦定律近似取为ξtanφbγz,ξ一般取0.2~0.4范围内; (2)抗滑桩在滑坡演化过程中始终保持竖直方向,即桩后侧正应力q始终保持水平方向; (3)计算深度z采用等效重力法(选用底边为y,高为z的矩形面积代替微段上面实际滑体重量图形面积); (4)设桩处滑带倾角不为0。

图 1 浅层滑体内滑坡推力分析模型Fig. 1 Thrust analysis model of landslide in shallow sliding mass a. 理论分析模型; b. 微段受力模型
如图 1所示的分析模型,以抗滑桩顶点为坐标轴原点,抗滑桩桩后侧水平方向为y轴正方向,竖直向下方向为z轴正方向。对于桩侧任一计算点,到滑带的水平距离为y,计算深度z采用等效重力法(选用底边为y,高为z的矩形面积代替微段上面实际滑体重量图形面积);W为微段上部滑体的等效重力(在深层滑体中时,需要考虑浅层滑带对深层滑体的作用力σ1,τσ1),c0、φ0为桩和滑体界面的黏聚力和内摩擦角,q,τq和σ,τσ分别为微段对应的桩土界面和滑带上的正应力和剪应力,τq和τσ取值按式(1)。
(1)
2 滑坡推力公式推导
由于不同层滑体间的相对运动,多层滑带启动顺序不同时,其滑坡推力分布存在一定差异。
当深层滑带先启动时,浅层滑体内滑坡推力计算如下:
根据图 1所示的分析模型,对水平微段隔离体进行受力分析,当桩后滑体处于极限平衡状态时,根据水平和竖直两个方向的静力平衡条件,可以解出桩后侧面的正应力:
Wy+τqdz+ydw+τσdz
=σcotθ1dz+(W+dW)(y-dzcotθ1)
(2)
τy+σdz+τσcotθ1dz
=qdz+τ(y-dzcotθ1)
(3)
式中:W=γz。
联立式(2)和式(3)可求得式(4)浅层滑体推力q1:
(4)
当深层滑带先启动时,深层滑体内滑坡推力计算如下:

图 2 深层滑体内滑坡推力分析模型Fig. 2 Thrust analysis model of landslide in deep sliding mass a. 理论分析模型; b. 微段受力模型
根据图 2所示的分析模型,对水平微段隔离体进行受力分析,当桩后滑体处于极限平衡状态时,根据水平和竖直两个方向的静力平衡条件,可以解出桩后侧面的正应力:
Wy+τqdz+ydw
=σcotθ1dz+(W+dW)(y-dzcotθ1)+τσdz
(5)
τy+σdz=qdz+τ(y-dzcotθ1)+τσcotθ1dz
(6)
联立式(5)和式(6)可求得式(7)深层滑体推力q2:
(7)
对于深层滑体来说,上部受到的重力可以等效为浅层滑带对下部作用的正应力和剪应力竖直向下的分量,以此做等效代换,如图 3。

图 3 W等效分析图Fig. 3 W equivalent analysis diagram
可求得等效W为式(8):
W=γ(z2-z1)+σcosθ1-τσsinθ1
(8)
联立式(6)和式(1)可解出:
(9)
(10)
将式(9)和式(10)代入式(8)可求得:
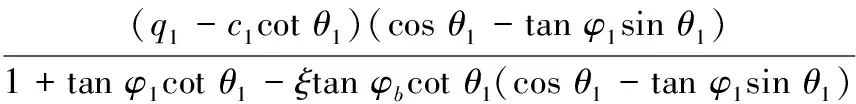
(11)
式中:c0,φ0为桩和滑体界面的黏聚力和内摩擦角;c1,φ1,θ1和c2,φ2,θ2分别为浅层滑带和深层滑带的黏聚力、内摩擦角和计算点水平向对应滑面上点的切线倾角;φb1,φb2分别为浅层滑体和深层滑体的内摩擦角。
当浅层滑带先启动时,浅层滑体内滑坡推力计算如下:
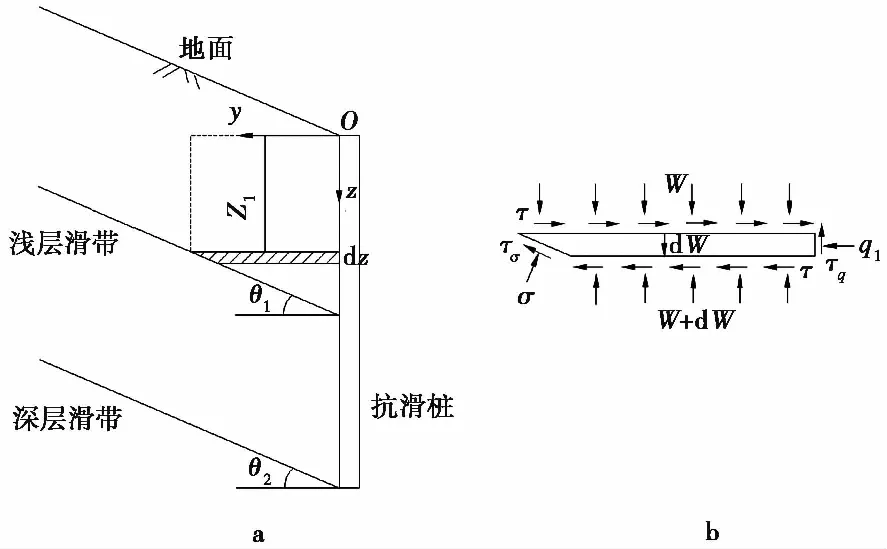
图 4 浅层滑体内滑坡推力分析模型Fig. 4 Thrust analysis model of landslide in shallow sliding mass a. 理论分析模型; b. 微段受力模型
根据如图 4所示的分析模型,对水平微段隔离体进行受力分析,当桩后滑体处于极限平衡状态时,根据水平和竖直两个方向的静力平衡条件,可以解出桩后侧面的正应力:
Wy+τqdz+ydw
=σcotθ1dz+(W+dW)(y-dzcotθ1)+τσdz
(12)
τy+σdz=qdz+τ(y-dzcotθ1)+τσcotθ1dz
(13)
式中:W=γz。
联立式(12)和式(13)可求得式(14)浅层滑体推力q1:
(14)
当浅层滑带先启动时,深层滑体内滑坡推力计算如下:
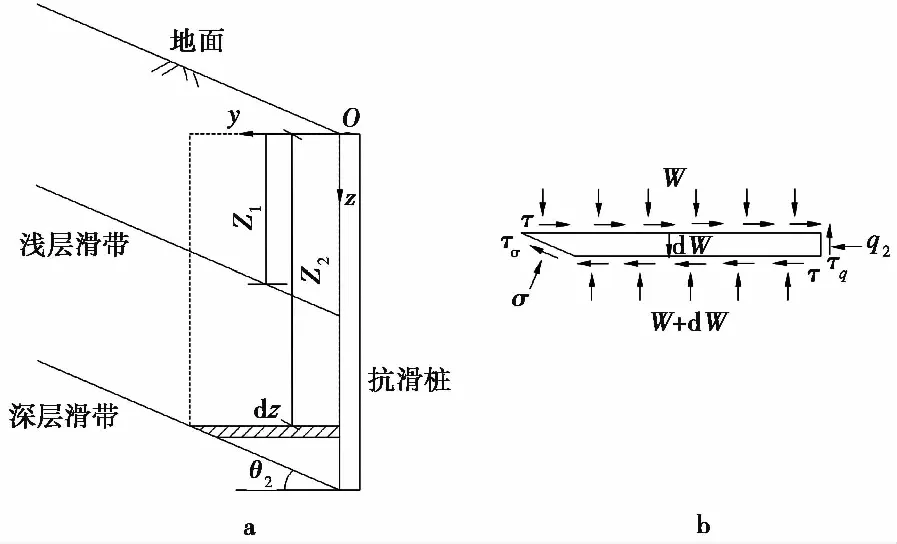
图 5 深层滑体内滑坡推力分析模型Fig. 5 Thrust analysis model of landslide in deep sliding mass a. 理论分析模型; b. 微段受力模型
根据如图 5所示的分析模型,对水平微段隔离体进行受力分析,当桩后滑体处于极限平衡状态时,根据水平和竖直两个方向的静力平衡条件,可以解出桩后侧面的正应力:
Wy+τqdz+ydw
=σcotθ1dz+(W+dW)(y-dzcotθ1)+τσdz
(15)
τy+σdz=
qdz+τ(y-dzcotθ1)+τσcotθ1dz
(16)
联立式(15)和式(16)可求得式(17)深层滑体推力q2:
(17)
对于深层滑体来说,上部受到的重力可以等效为浅层滑带对下部作用的正应力和剪应力竖直向下的分量,以此做等效代换,如图 6所示。

图 6 W等效分析图Fig. 6 W equivalent analysis figure
可求得等效W为式(18):
W=γ(z2-z1)+σcosθ1+τσsinθ1
(18)
联立式(13)和式(1)可解出:
(19)
(20)
将式(19)和式(20)代入式(18)可求得:
(21)
基于该方法,将两层滑带滑坡推广到n层滑带滑坡,可得到如下结论:
当多层滑带滑坡的n层滑带由深到浅依次启动时,第i层滑体内滑坡推力公式。
当1≤i (22) 当i=n时: (23) 当多层滑带滑坡的n层滑带由浅到深依次启动时,第i层滑体内滑坡推力为: (24) 为了验证前文多层滑带滑坡推力分布计算方法的可靠性,选取马家沟多层滑带滑坡为研究对象,将理论计算与数值模拟计算结果进行对比分析。本文多层滑带滑坡数值模拟的主要研究目的是得到滑坡推力分布和抗滑桩内力分布特征。根据现场监测数据(张玉明, 2018),使用FLAC3D软件采用局部三维模型计算,建立计算模型如图 7所示,滑坡模型长625m,宽22m,高216m,共划分71195个节点和87600个网格单元。滑坡重点研究区域为多层滑带和设桩位置附近,在此区域附近加密网格重点分析。模型的边界条件设定为速度为0的固定边界,四周及底面均设置为法向约束,坡表不设约束。 图 7 马家沟多层滑带滑坡局部三维数值模型Fig. 7 Local three dimensional numerical model of Majiagou multi-sliding sliding zone landslide-pile system 根据现场布设情况,在模型中部建立3根矩形抗滑桩,桩长40m,截面尺寸为2.0m×3.0m,具体尺寸和位置如图 7所示。抗滑桩位置浅层滑带、中层滑带及深层滑带深度分别为12m、18m和26m。计算模型材料参数如表 1所示,取值参考了土工试验数据和前人研究成果(张玉明, 2018)。考虑数值模拟计算的复杂性,本文未能考虑地下水作用的影响。 表 1 计算模型材料物理力学参数取值表Table1 Values of physical and mechanical parameters of calculation model materials 表 2 计算模型桩土接触面参数取值表Table2 Parameter values of pile-soil interface of calculation model 图 8 多层滑带滑坡推力计算结果对比图Fig. 8 Comparison of thrust calculation results of multi-layer sliding zone landslide 采用实体单元建立抗滑桩,在桩土接触界面采用接触面单元进行模拟,抗滑桩和岩土体接触面参数如表 2所示。 通过数值模拟计算,得到了马家沟多层滑带滑坡推力分布图式,如图 8所示。根据数值模拟计算结果,通过监测滑带处位移可知滑坡在演化过程中滑带整体由深到浅依次启动,同时滑坡位移由前缘逐步向后缘发展。因此水平微段极限平衡法理论计算中设定3层滑带由深到浅依次启动; 通过多次试算,当理论计算取ξ=0.35时,理论计算结果和数值模拟计算结果基本一致,计算结果如图 8所示。 数值模拟计算结果显示多层滑带滑坡推力随深度增加而不断增大,在浅层滑体内符合三角形分布,在中层滑体和深层滑体内滑坡推力数值虽有波动,但基本符合梯形分布,波动原因可能是数值模型网格划分不够精细。 由图 8可知,在浅层滑带处滑坡推力突然增大,在中层滑带处滑坡推力突然减小。其原因是中层滑体相对于浅层滑体向下滑动,浅层滑体下方受到顺坡向的摩擦力,因此浅层滑带处推力突然增大。由图 7可知,马家沟滑坡中层滑带为中前缘局部滑带,在桩前与深层滑带形成了整体滑动,同时滑坡位移前缘逐步向后缘发展,桩后区域中层滑体相对于深层滑体顺坡向滑动,中层滑带处受到逆坡向的摩擦力,因此中层滑带处滑坡推力突然减小。 由数值模拟和水平微段极限平衡法理论计算两种结果对比可知,两者抗滑桩桩后推力分布模式与大小基本相似,说明了本文方法的可靠性。 (1)在前人研究的基础上,分析得出了多层滑带滑坡推力分布函数存在分段的特征; 根据水平微段极限平衡状态下的受力分析,通过竖直方向和水平方向的受力平衡求解出了每层滑体内的滑坡推力。 (2)分析竖直方向的受力平衡时,需要考虑不同层滑体向下的受力传递,导致滑坡推力分布函数在滑带处存在突变; 通过理论推导将两层滑带滑坡推力公式推广到n层滑带滑坡中,得到了多层滑带滑坡抗滑桩桩后推力计算分布函数。 (3)选取马家沟多层滑带滑坡为工程案例,将水平微段极限平衡法理论与数值模拟计算结果进行了对比分析,对比结果验证了本文多层滑带滑坡抗滑桩桩后推力分布计算方法的可靠性,为多层滑带滑坡的防治理论提供了一定的参考。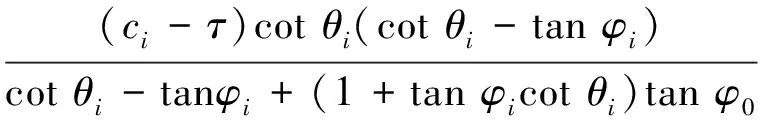

3 工程案例验算




4 结 论
