两台对称六相PMSM反串联系统的建模与仿真
2022-02-11刘陵顺闫红广
刘陵顺,孙 旭,闫红广
(1.海军航空大学 航空基础学院,烟台 264001; 2.人民解放军92407部队,烟台 264001)
0 引 言
相对于传统三相电机而言,多相电机具有功率密度高、电压电流等级低、转矩脉动小、静音、高效、兼具容错性等优点,因而被应用于航空航天、船舶机车驱动以及风力发电等领域[1-2]。但是多相电机需要较多的逆变器相数,也带来体积、质量和费用增大的问题,这可以通过多台电机定子绕组串联的方式由同一套逆变器同时独立驱动来解决[3-6],这种多电机串联系统对于电机的类型没有要求,其联结方式和工作原理在文献[3]中已有报道。
多电机串联系统能够独立运行的基本条件是电机的反电动势必须按正弦规律分布。而对于2台对称六相永磁同步电机(以下简称PMSM)或4台对称十相PMSM,只需要永磁转子结构对称而无需电机正弦反电动势的要求,即可采用某种定子绕组反串联的方式,同样可以实现同一逆变器驱动下的独立运行[7]。
本文针对两台对称六相PMSM反串联系统开展研究,建立了双电机反串联系统在不同坐标系下的数学模型,利用id=0的电流滞环PWM控制策略,对反串联系统进行了稳态仿真,实现了对反串联系统的解耦控制。
1 双电机反串联系统的数学模型
如图1所示[7],在两台对称六相PMSM反串联系统中,电机相绕组按照一定的相序规则进行反串联,其中,两台电机的A相、C相、E相直接相连,B相、D相、F相反向串联。
1.1 自然坐标系下的数学模型
根据图1中的反串联连接方式,可得六相逆变器输出电压:
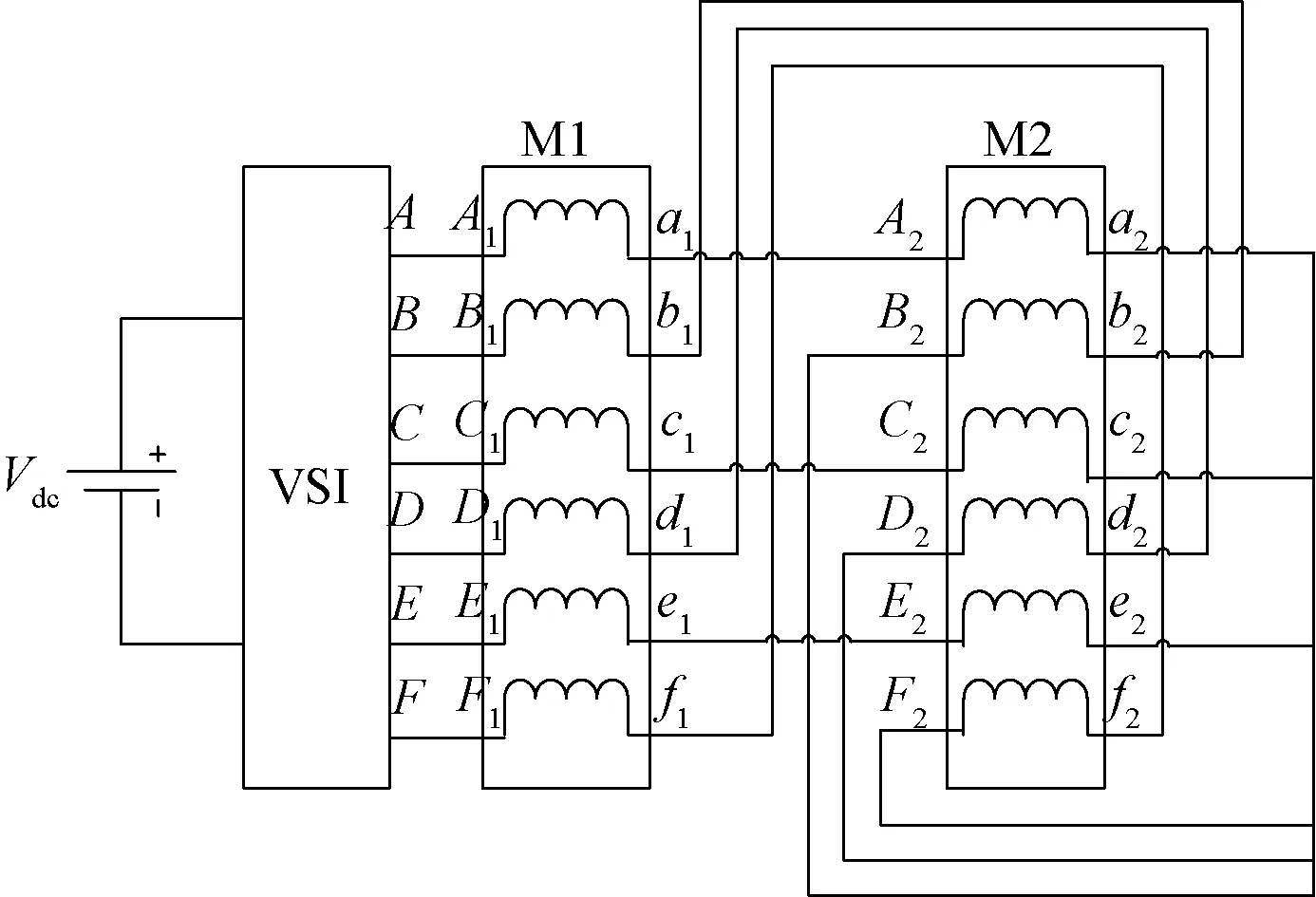
图1 两台对称六相永磁同步电机反串联系统
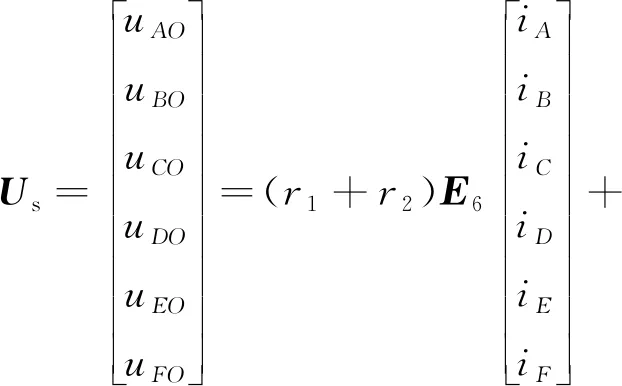
(1)
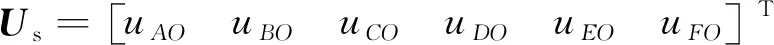
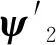

(2)
式中:L′2是第二台对称六相PMSM电感矩阵L2的扩展;ψ′r2是ψr2的扩展。则两台对称六相PMSM反串联系统的定子磁链:
(3)
1.2 静止坐标系下的数学模型
解耦变换矩阵T6可以将两台对称六相PMSM反串联系统的数学模型从自然坐标系下变换到静止坐标系下。
(4)
式中:T6的前两行对应第一台对称六相PMSM的基波平面,为αβ平面;中间两行对应第二台对称六相PMSM的基波平面,为xy平面;最后两行对应零序平面,为o1o2平面。两台对称六相PMSM反串联系统在静止坐标系下αβ平面,xy平面,o1o2平面内的定子磁链表达式分别如下:
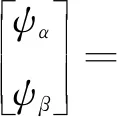
(5)

(6)
(7)
在静止坐标系下,第一台对称六相PMSM的转矩表达式:

p1(ψαiβ-ψβiα)
(8)
同理可得静止坐标系下,第二台对称六相PMSM的转矩表达式:
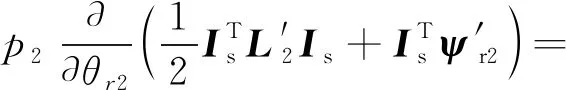
p2(ψxiy-ψyix)
(9)
用T6将自然坐标系中的两台对称六相PMSM反串联系统的电压方程变换到静止坐标系中:
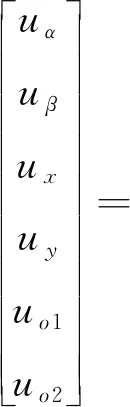
(10)
整理可得:
(11)
(12)
(13)
通过式(11)~式(13)可以看出:αβ平面主要包含第一台对称六相PMSM的与机电能量转换相关的量,还包含第二台对称六相PMSM的漏磁和电阻压降部分,这部分不会影响第一台电机的转矩,可以等效到第一台电机的漏磁和电阻压降部分中去,而第一台电机在其他平面只有漏磁和电阻压降部分,同样也不影响其转矩,所以控制αβ平面的电压就可以达到控制第一台电机转矩的目的;xy平面主要包含第二台电机的与机电能量转换相关的量,还包含第一台电机的漏磁和电阻压降部分,这部分不会影响第二台电机的转矩,可以等效到第二台电机的漏磁和电阻压降部分中去,而第二台电机在其他平面只有漏磁和电阻压降部分,同样也不影响其转矩,所以控制xy平面的电压就可以达到控制第二台电机转矩的目的;o1o2平面只有两台电机的漏磁和电阻压降部分,不影响两台电机的转矩,但与电机效率有关,控制o1o2平面的电压可以提高反串联系统效率。由此可见,两台电机能够实现独立解耦控制。
1.3 旋转坐标系下的数学模型
令静止坐标系到旋转坐标系的旋转变换矩阵:
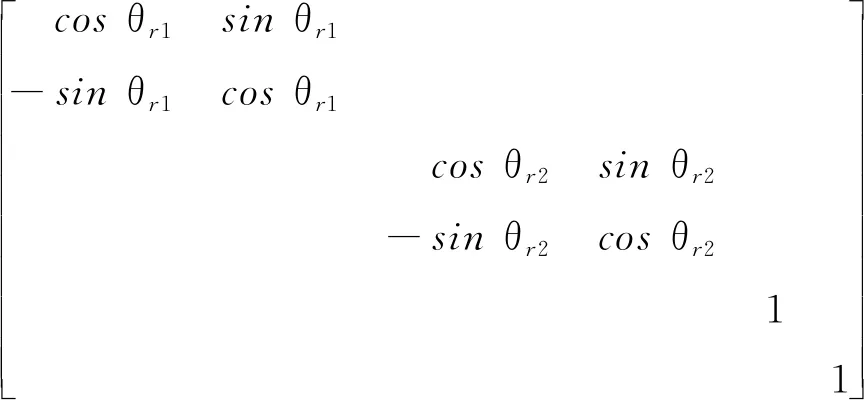
(14)
用变换矩阵R1将式(5)、式(10)变为:
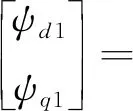
(15)
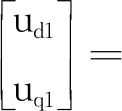
(16)
式中:Ld1=Lsσ1+Lsσ2+3Lsm1+3Lsr1,Lq1=Lsσ1+Lsσ2+3Lsm1-3Lsr1分别为d1,q1轴电感。
第一台对称六相PMSM的转矩表达式可变为:
Te1=p1(ψd1iq1-ψq1id1)
(17)
同理,用变换矩阵R2将式(6)、式(11)变为:
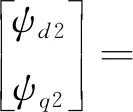
(18)

(19)
式中:Ld1=Lsσ1+Lsσ2+3Lsm2+3Lsr2,Lq1=Lsσ1+Lsσ2+3Lsm2-3Lsr2分别为d2,q2轴电感。
第二台对称六相PMSM的转矩表达式可变为:
Te2=p2(ψd2iq2-ψq2id2)
(20)
2 运行性能仿真
基于id=0矢量控制的两台对称六相PMSM反串联系统的控制框图如图2所示。
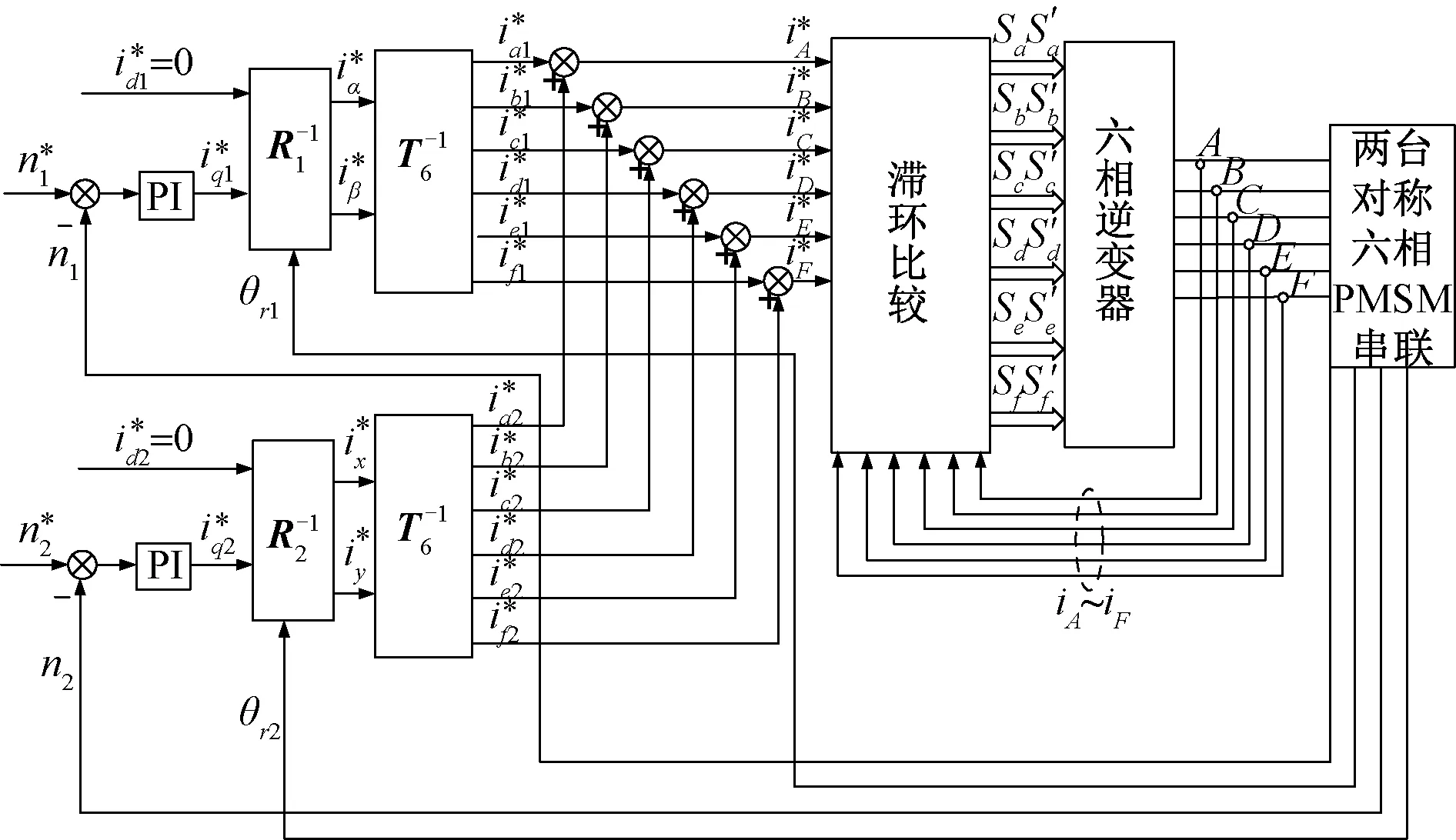
图2 反串联系统的滞环控制
基于id=0的电流滞环PWM控制策略,通过直接控制旋转坐标系下的交轴电流iq1、iq2,从而控制两台电机的转矩。图2中,通过实际转速与期望转速得到旋转坐标系下的给定电流值iq1、iq2。基于id=0的控制策略,将iq1、iq2反变换到自然坐标系下(同一六维平面),叠加后即为六相逆变器的期望输出电流。当逆变器某相的实际电流值大于算法给定的期望电流值时,下一控制周期关闭该桥臂;反之,则使该相继续导通。如此确定下一周期六相逆变器各桥臂的期望开关状态。
电机参数如下:Lsm1=Lsm2=1.17 mH,Lsr1=Lsr2=0.46 mH,Lsσ1=Lsσ2=0.83 mH,p1=p2=2,R1=R2=1 Ω,Ψf1=Ψf2=0.2 Wb。当第一台电机的转速为400 r/min、负载为4 N·m,第二台电机的转速为200 r/min、负载为2 N·m时,两台对称六相PMSM反串联系统的稳态运行仿真结果如图3~图6所示。
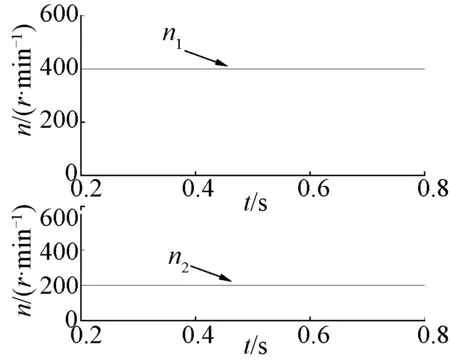
图3 两台电机的转速
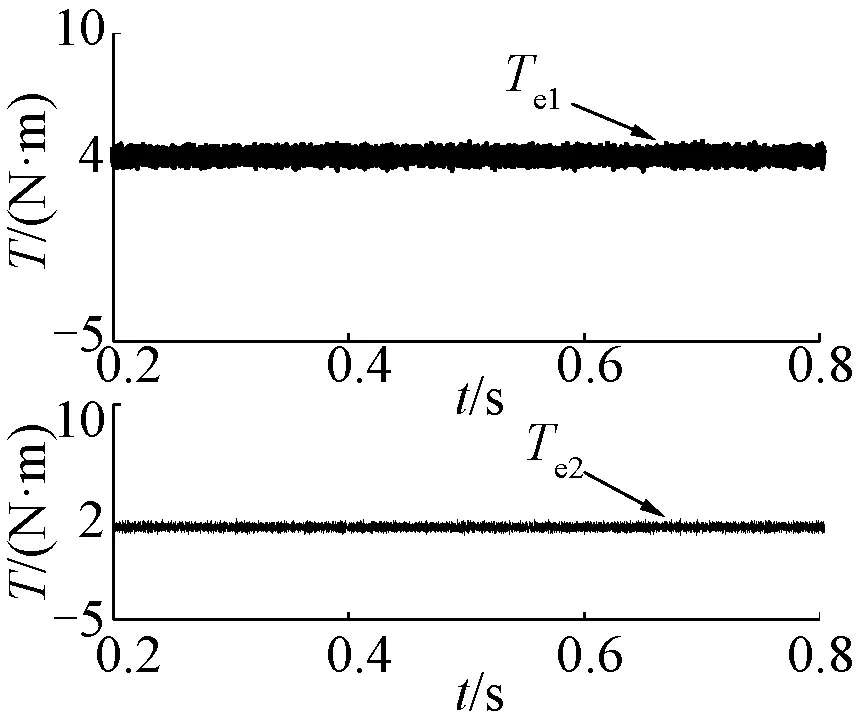
图4 两台电机的转矩
当两台对称六相PMSM反串联系统稳态运行时,由图5可知,两台对称六相PMSM在静止坐标系下的电流都为正弦波,达到了控制要求,与两台电机平稳的转矩和转速相对应。
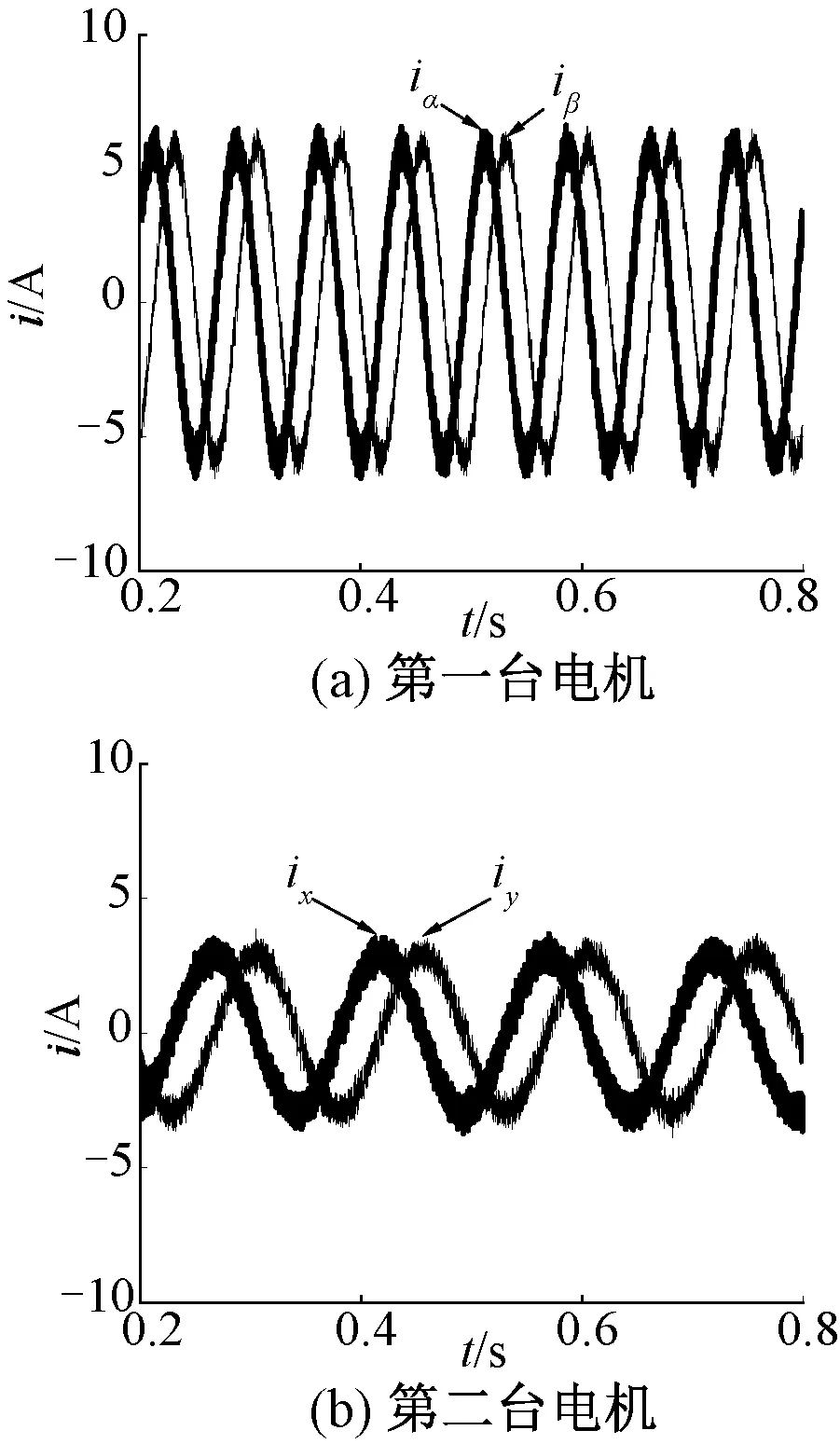
图5 静止坐标系下两台电机的电流
由图6可知,两台对称六相PMSM在自然坐标系下的各相电流均不为理想正弦波,各相电流波形中均包含两种频率成分,这两种频率成分与两台电机的转速相对应,同时,两台电机的A、C、E相电流波形相同,B、D、F相电流波形相反,这与反串联的连接方式相一致。
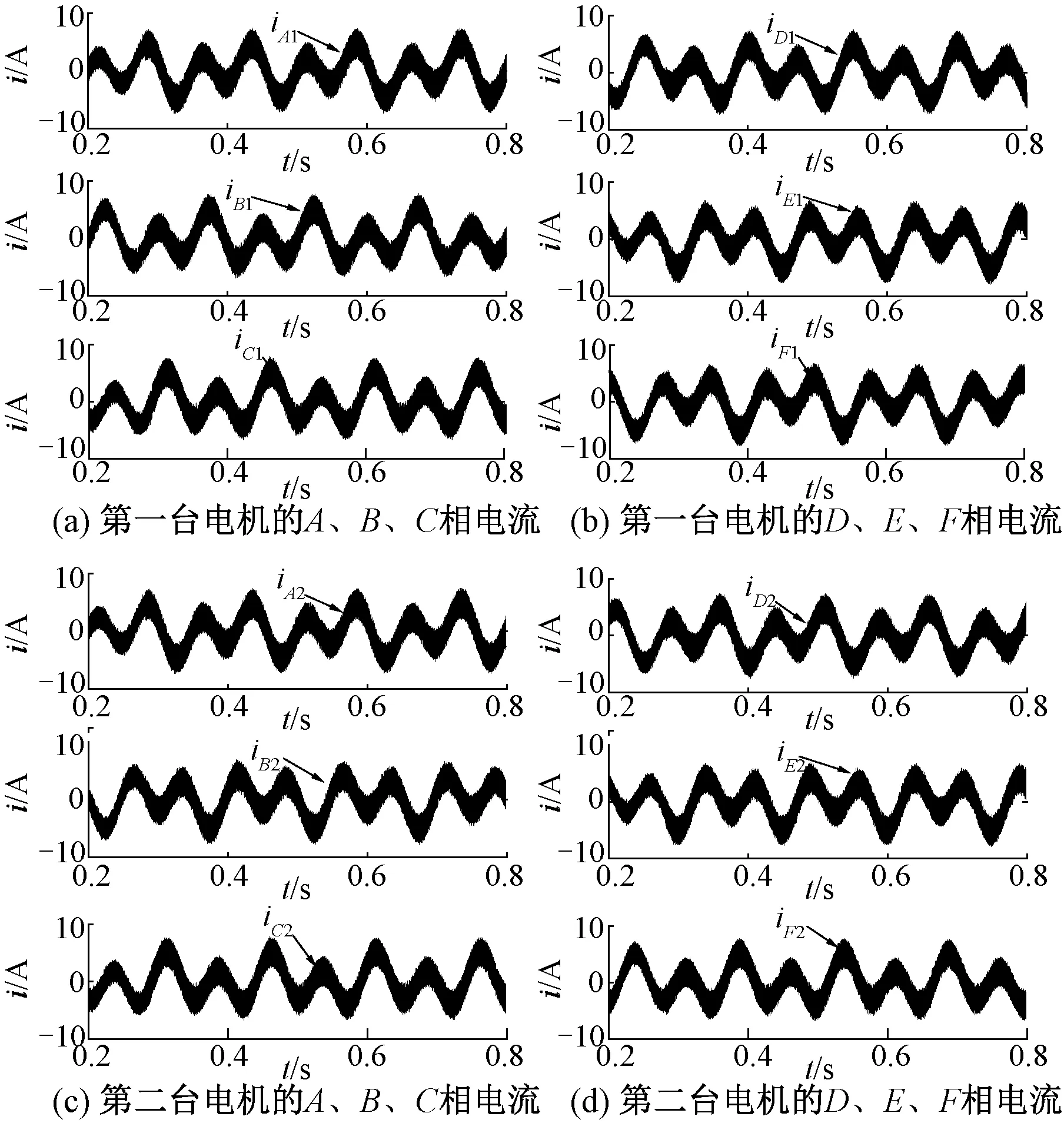
图6 自然坐标系下两台电机的电流
3 结 语
本文以反串联的两台对称六相PMSM系统为研究对象,分别在自然坐标系、静止坐标系和旋转坐标系中建立了单逆变器供电的两台凸极式对称六相PMSM反串联系统的电压和磁链方程,得到了两台电机的转矩表达式,并利用id=0的电流滞环PWM控制策略对反串联系统进行了稳态仿真分析,仿真结果表明该控制策略实现了对反串联系统的解耦控制。
