基于ANN-GA 协同寻优的动态拉伸试样尺寸优化方法*

王清华，徐 丰，郭伟国

（1. 西北工业大学航空学院，陕西 西安 710072；2. 西北工业大学航天学院，陕西 西安 710072；3. 西北工业大学青岛研究院，山东 青岛 266200）

高性能合金、聚合物、复合材料广泛应用于航空航天、国防工程等领域，在服役过程中不可避免地承受爆炸、冲击等动态载荷。由于材料在动态载荷下往往表现出不同于（准）静态的力学性能，因此，研究材料的动态力学性能对于结构安全设计和强度校核等具有重要意义。

目前，研究材料在高应变率（10～10s）下力学性能的典型实验装置为分离式霍普金森杆（split Hopkinson bar, SHB），特别地，对于材料动态拉伸性能的测试常采用分离式霍普金森拉杆（split Hopkinson tensile bar, SHTB）。SHTB 在结构上的改进主要表现在两方面：（1）脉冲的激励方式，目前广泛采用的激励方式源自Ogawa的设计，通过套在入射杆上的管状子弹撞击入射杆前端的法兰产生加载脉冲；（2）试样的设计，不同于压缩试样，拉伸试样的结构一般分为连接段、过渡段和标距段3 部分，连接段常采用螺纹、销钉、胶粘等连接形式实现与杆的相连。对于薄板等无法或不便进行车削加工的型材，螺纹连接在进行试样设计时明显不适用，只能选择基于胶粘或销钉等片状试样所适用的连接形式，其中，结构简单且连接组装效率高的连接形式当数销钉连接。

动态拉伸试样的结构尺寸对实验测得的材料动态拉伸性能具有一定的尺寸效应，即在相同的加载工况下对同种材料进行动态拉伸测试，采用不同尺寸的拉伸试样所测得的动态拉伸力学性能有一定的差异。事实上，动态拉伸试样尺寸对实验测得材料动态拉伸力学性能的影响长时间以来都备受关注，相应的试样结构尺寸优化工作也在不断地进行。以往采用的试错法或控制变量法因其自身的局限性，难以实现试样结构参数对材料动态拉伸力学性能测量准确度影响规律的深层次挖掘，此外，由于样本空间极为有限，使试样结构优化无法在整个参数空间内进行，从而只能得到试样结构尺寸的次优解。

鉴于现有优化方法的局限性，本文中以SHTB 中基于销钉连接形式的片状拉伸试样为例，介绍一种针对动态拉伸试样结构尺寸优化的人工神经网络（artificial neural network, ANN）与遗传算法（genetic algorithm, GA）协同寻优的优化方法。首先，提出量化的、能够衡量试样测量准确度的指标，即应力平衡达到时间、变形均匀度、非轴向应力相对水平以及过渡段相对变形。然后，对试样结构参数进行正交试验设计并通过数值模拟建立关于试样结构尺寸与测量准确度指标的正交试验数据库。采用多目标正交试验矩阵分析法对正交试验数据库进行数据挖掘，得到试样结构参数对各项测量准确度指标影响的主次顺序和规律。以正交试验数据库为训练集对ANN 进行训练，得到能够根据试样结构尺寸准确预测相应测量准确度指标的ANN 模型，并基于该模型构建GA 中的适应度函数。最后，通过GA 寻优得到片状动态拉伸试样的最优结构尺寸，并对最优结构尺寸的有效性进行验证。

1 材料动态拉伸力学性能测试

1.1 动态拉伸测试原理

材料动态拉伸力学性能测试的典型实验装置为SHTB，其测试原理如图1 所示。撞击管自右向左运动并撞击位于入射杆前端的法兰产生沿入射杆右行的拉伸入射波。当入射波到达试样与入射杆的交界面时，一部分以压缩波的形式发射回入射杆形成左行的反射波，另一部分透过试样继续以拉伸波的形式沿透射杆传播形成透射波。反射波 ε() 和透射波 ε() 可分别由粘贴在入射杆和透射杆上的应变片测得，试样的应变率、应变和应力可通过下式计算获得：

图1 分离式霍普金森拉杆装置Fig. 1 The split Hopkinson tensile bar device

式中： ε˙ 为试样应变率， ε 、 σ 分别为试样应变和应力，、分别为杆的弹性模量和弹性波速，为试样标距段长度，、分别为杆和试样的截面积。

1.2 片状动态拉伸试样形式

1.2.1 试样尺寸参数与正交试验设计

以销钉连接形式为例，片状动态拉伸试样的结构如图2 所示。试样结构分为标距段（gauge section）、过渡段（transition section）和连接段（connection section）3 部分。连接段中心位置开有销钉孔并配合销钉实现与杆的连接，标距段为试样变形和受力的测量区域，而过渡段则用于连接段与标距段间的过渡连接。试样尺寸参数及其惯用值见表1。

表1 片状动态拉伸试样结构参数及其惯用值Table 1 Structural parameters of the sheet specimen used for dynamic tensile tests and the reference values

图2 基于销钉连接的拉伸试样结构Fig. 2 The structure of tensile specimens based on the pin connection

正交试验设计法简称正交法，是一种使用正交表（一种按特定规则设计的表格）来设计试验，并利用正交表的特点对试验结果进行分析的试验方法。采用正交法产生的样本分散度高、均匀性好，代表性强。以结构参数的惯用值为中间水平，以结构参数作为因素，建立的六因素五水平正交表(5)见表2。正交表不仅为多目标正交试验矩阵分析提供了样本，也为神经网络训练提供了示例。

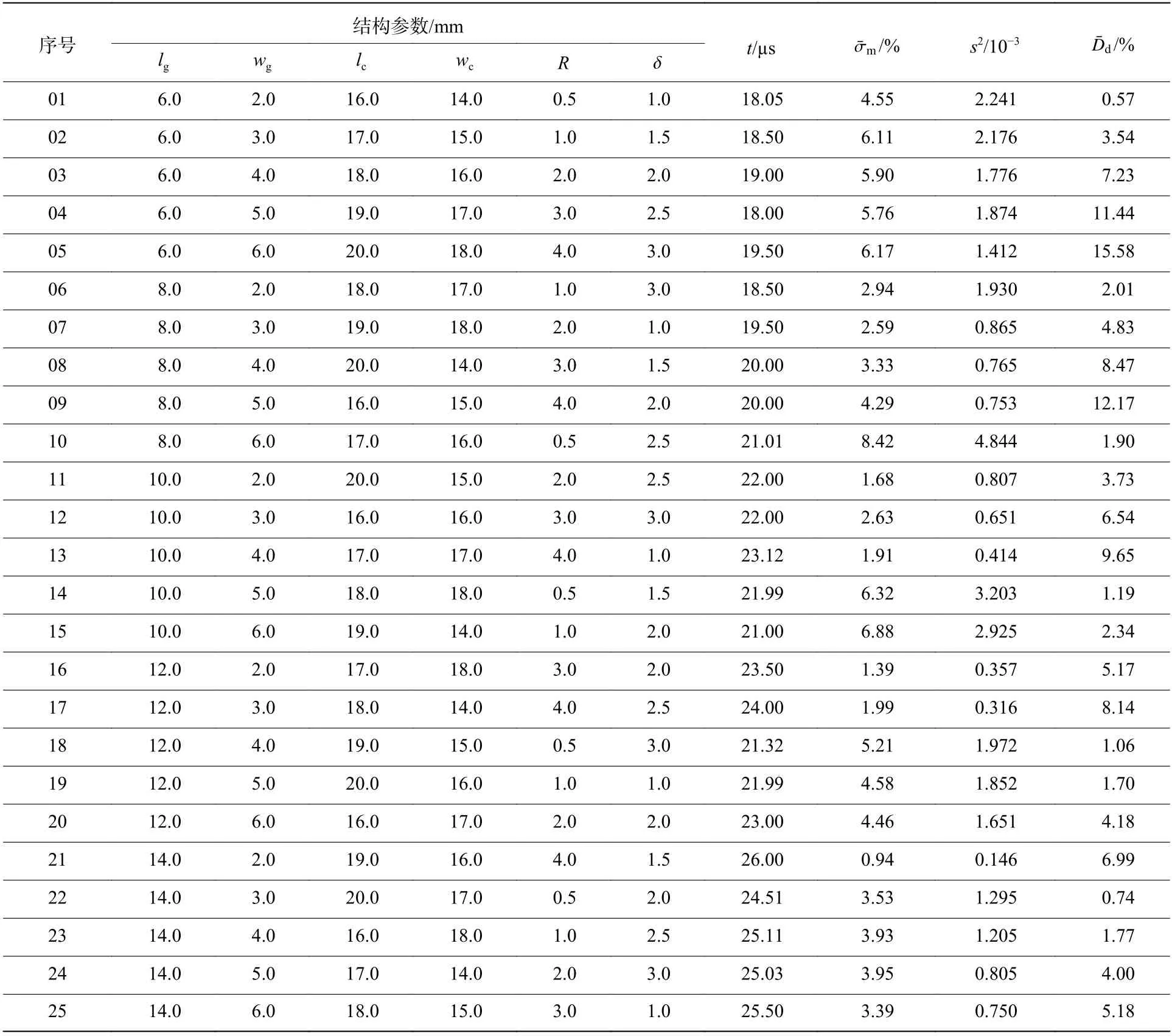
表2 试样结构参数正交表与模拟结果Table 2 Orthogonal table of the specimen structural parameters and the simulation results

1.2.2 基本假设与测量准确度指标

根据SHTB 的测试原理和一维弹性应力波理论，实验测得材料动态拉伸力学性能的有效性和准确性要求试样在整个动态拉伸过程中需满足以下4 个基本假设。

（1）应力平衡假设：拉伸试样标距段前后端面上的应力大小相等。

（2）变形均匀假设：动态拉伸过程中试样标距段沿轴向均匀变形。

（3）一维应力假设：杆与试样中的应力状态为轴向上一维应力。

（4）过渡段零变形假设：动态拉伸过程中过渡段在轴向上不变形。

与4 个基本假设相对应，提出了可以量化试样测量准确度的指标。为了便于说明，图3 为试样有限元模型，具体地，图3(a)为试样的全模型，图3(b)为标距段与过渡段的1/4 模型。图3(b)中，点、为试样中心轴线上过渡段与连接段的交点，点、为试样中心轴线上标距段与过渡段的交点。

图3 销钉连接拉伸试样的有限元模型Fig. 3 The finite element models of the pin-connected tensile specimen

（1）应力平衡达到时间：自入射波到达试样标距段前端面起直至应力平衡判据Δσ 小于5%的时间间隔。判据 Δσ 的具体形式为：

式中： σ、 σ分别为图3(b)中、点的轴向应力。

（2）变形均匀度：单波加载结束后点、间各节点轴向应变的方差。的具体形式为：

式中： σ、 σ分别为节点上法向应力和轴向应力，为节点个数。

式中：、分别为点、之间及点、之间的轴向变形，为点、之间的轴向变形。

2 SHTB 动态拉伸有限元模拟

2.1 模型建立

SHTB 的动态拉伸有限元模拟采用商用有限元软件ABAQUS(Explicit)。入射杆长为2 800 mm，直径为20 mm；透射杆长为1 200 mm，直径为20 mm；撞击管外径为28 mm，内径为20.5 mm，长度为500 mm；法兰长10 mm，外径为28 mm；销钉直径为5 mm，长度为25 mm，头部为边长5.2 mm、厚度3.5 mm的正六棱柱体。在试样及其连接区域对网格进行细化，其他区域由于只是起到激励和传播波形的作用而不做细化处理，网格效果如图4 所示，四面体网格类型为C3D4，六面体网格类型为C3D8R。撞击管与法兰、试样与杆、销钉与杆、销钉与试样间接触面的接触属性均设置为摩擦因数为0.2 的面-面接触。采用施加初始速度场的方法代替高压气体驱动实现子弹与法兰的碰撞，调整子弹初始速度场的幅值，使得试样应变率位于[1 500 s，2 000 s]。

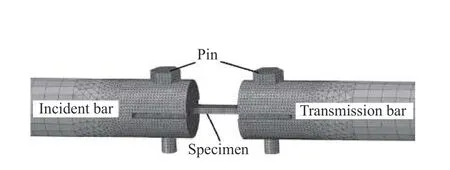
图4 试样与杆端的网格模型Fig. 4 Mesh of the specimen and bar ends

模拟时，假定杆、撞见管以及销钉材料为45 钢，试样材料为AA7075-T6 铝合金。由于在实际测试中，杆、撞击管、销钉始终处于弹性段，而试样先经历弹性阶段再屈服进入塑性流动段，因此45 钢采用线弹性模型，而AA7075-T6 采用线弹性模型和Johnson-Cook 塑性本构模型。

Johnson-Cook 模型描述了一定温度和应变率下材料等效流动应力与等效塑性应变之间的关系，其具体形式为：

表3 模拟用材料模型参数Table 3 Parameters of the material model used for simulations

2.2 模型验证

为了验证2.1 节中建立的数值模型是否能够有效、准确地模拟真实实验，对1 200 s应变率下AA7075-T6 动态拉伸力学性能的实验测试结果与模拟结果以及模拟所采用的Johnson-Cook 模型进行了对比，结果如图5 所示。可以看出，模拟所得材料动态拉伸力学性能虽然存在较明显的抖动，但其与实验实测所得材料动态拉伸力学性能在趋势上基本一致，且与所采用的材料模型也基本吻合。因此，2.1 节中建立的数值模型不仅可以准确反映试样被定义的材料模型，也能够准确模拟真实实验，数值模型具有很好的拟真性。而造成模拟结果曲线存在明显抖动的原因可能是，模拟中没有考虑波形整形问题，且有限元模型的接触条件过于理想，导致波形中相当宽频范围内的各频率成分均能够在试样、销钉及杆的接触面间有效传播，从而导致反射波与透射波因较严重的波形弥散而出现明显的抖动；又由于Hopkinson 杆测量的间接属性，即材料应力-应变曲线需由反射波和透射波解算得到，见式（1）, 尤其是透射波，其构型将直接决定应力-应变曲线中应力成分的构型，因此，反射波与透射波的抖动直接造成了应力-应变曲线的抖动。此外，需要说明的是，图5 横纵坐标中的应变和应力对于实验和模拟结果曲线分别为真实应变、真实应力，而对于Johnson-Cook 模型曲线则分别为等效塑性应变和等效流动应力。

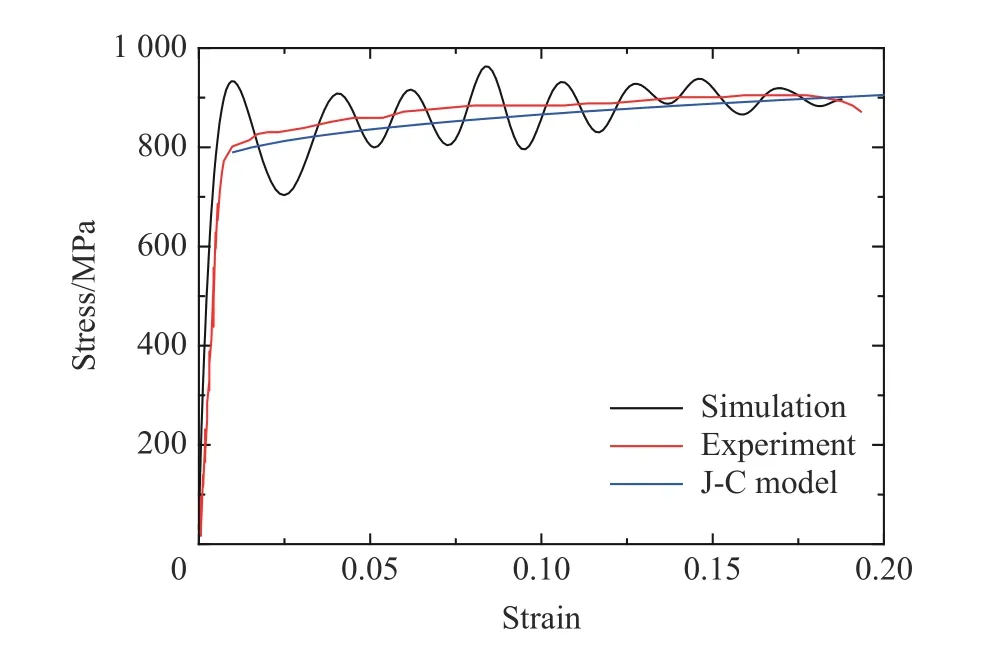
图5 材料动态拉伸力学性能的数值模拟、实验以及模型对比Fig. 5 Comparison of the dynamic tensile mechanical properties from simulation, experiment and material model

2.3 模拟结果

1.2.2 节中的正交试验设计得到了25 组尺寸各异的试样，利用2.1 节中建立的数值模型对各组试样进行动态拉伸模拟，得到了各组试样所对应的测量准确度指标，结果见表2。

3 试样尺寸效应分析

多目标正交试验矩阵分析属于数据挖掘的一种，该方法可以根据正交表的特点计算出正交试验中各因素、各水平对试验指标的影响权重，而根据权重的大小可以确定各因素对试验指标影响的主次顺序和规律。正交试验矩阵分析方法的详细介绍见文献[26]。

由权重矩阵，试样结构参数对各测量准确度指标影响的主次顺序及规律见表4。

图6 正交试验数据库结构示意图Fig. 6 Data structure of the orthogonal test database

表4 试样结构参数对测量精度指标影响的主次顺序及规律Table 4 The influence order and law of the specimen structural parameters on the measurement accuracy indicators

4 试样尺寸的ANN-GA 协同优化

4.1 ANN 模型

4.1.1 模型建立与训练

为实现在整个参数空间内对试样的结构尺寸进行寻优所需要解决的最关键问题是建立试样结构参数与测量准确度指标间的非线性映射关系，而这一映射关系很难通过解析法获得。以ANN 为代表的人工智能或机器学习方法在非线性建模方面取得了丰硕的成果，无论建模效率还是建模精度均不逊于解析模型。因此，本文中采用ANN 拟合试样结构参数与测量精度指标之间的非线性映射关系。

典型的ANN 模型如图7 所示，模型从结构上共分为3 层：输入层、隐含层和输出层。神经网络的学习训练机制可以概括为信息正向传递、误差反向传播，其中，信息的传播机制如下：

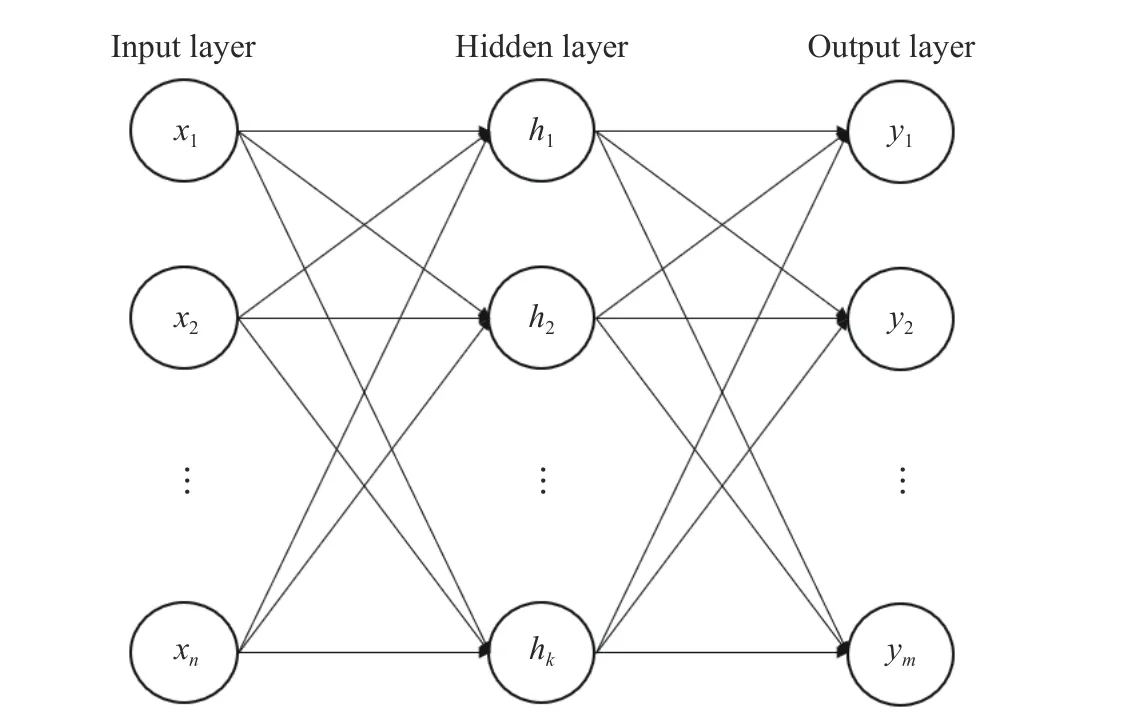
图7 神经网络模型结构示意图Fig. 7 Schematic diagram of the neural network model structure

4.1.2 模型有效性验证

为了验证网络模型的泛化性能，设置了表5 所列有别于训练集的3 组试样作为验证集。验证集上模型的预测值与相应的真实值之间的对比见表6。可以看出，验证集上模型预测值与真实值之间的最大相对误差仅10.48%，平均误差低至6.03%。这说明，4.1.1 节中训练的网络模型具有较强的泛化能力，可以根据试样结构准确预测对应的测量精度指标，模型具有有效性。

表5 验证集Table 5 Validation data set

表6 验证集真实值与预测值的对比Table 6 Comparison of the true and predicted values of the validation dataset

4.2 GA 寻优

GA 是模拟生物进化论中的自然选择和遗传学中的生物进化的计算模型，是一种通过模拟自然进化过程、原理简单且应用广泛的最优解搜索方法。GA 通过适应度函数的构建实现与ANN 的协同，基于ANN 构建的适应度函数如下：

图8 神经网络与遗传算法协同优化方案Fig. 8 Collaborative optimization scheme of neural network and genetic algorithm

4.3 优化结果与有效性验证

GA 模拟进化进行寻优的过程如图9 所示，纵坐标记录了每一代中最优个体的适应度值，即最小适应度值。模拟进化过程中，每代最优个体的适应度值先迅速减小，后趋于稳定，最终达到收敛，表明以式(11)为适应度函数的遗传算法可有效实现试样结构尺寸的寻优。

图9 GA 模拟进化寻优过程Fig. 9 Optimization process simulated by GA

图10 为ANN-GA 协同优化后的试样结构与尺寸，优化后的试样与惯用尺寸试样测量准确度指标的对比见表7。可以看出，优化后试样的各项测量准确度指标都有所降低，尤其应力平衡达到时间和非轴向应力相对水平均大幅减小，表明尺寸优化后的试样在测量准确度上的表现显著提高，ANN-GA 协同寻优的动态拉伸试样尺寸优化方法切实有效。此处需要说明的是，图10 中试样最优尺寸具有材料相关属性。事实上，动态拉伸过程中试样过渡段相对变形、标距段变形均匀度等在很大程度上受材料动态属性的影响。因此，图10 中试样最优尺寸适用于性能和AA7075-T6 型铝合金相近或类似的材料。而对于硬化相对AA7075-T6 不明显的材料，动态拉伸过程中过渡段相对变形将变得不明显，此时适当增大试样的过渡段半径将有利于动态拉伸过程中变形的均匀度和应力的一维性。其他性能差距悬殊的材料可采用本文方法在替换样本集后重新建模寻优得到。

表7 优化前后试样测量准确度指标对比Table 7 Comparison of the measurement accuracy indicators of specimens before and after optimization

图10 优化后试样结构及尺寸（单位：mm）Fig. 10 Optimized specimen structure and dimensions (unit: mm)

5 结 论

以SHTB 中销钉连接形式的片状拉伸试样为实例，提出了一种ANN-GA 协同以实现在整个参数空间内对动态拉伸试样结构尺寸进行优化的优化方法。首先，基于SHTB 的测试原理提出了可以量化试样测量准确度的指标。然后，对试样结构参数进行正交试验设计并通过有限元模拟建立了正交试验数据库。对正交试验数据库应用多目标正交试验矩阵分析得到了试样结构参数对测量准确度指标影响的主次顺序和规律。最后，以正交试验数据库为训练集，采用ANN-GA 协同寻优得到了试样的最优结构尺寸。通过上述工作可以得出以下结论。

（1）采用多目标正交试验矩阵分析的数据挖掘方法可对动态拉伸试样结构参数影响试样测量准确度指标的机制和规律进行基于数据驱动的深层次挖掘。

（2）ANN 模型可有效应用于试样结构尺寸与测量准确度指标之间的非线性建模，训练后的ANN 可根据试样结构尺寸准确预测具有该尺寸的试样所对应的测量准确度指标。

（3）协同基于ANN 构建的适应度函数，GA 可实现动态拉伸试样结构参数寻优过程的收敛，ANNGA 协同优化方法对于动态拉伸试样结构尺寸优化切实有效。