基于ICS-GRNN 的油气管道剩余强度预测技术

0 前 言

目前， 我国管道建设正在向大直径、 高强度、高钢级的方向发展， 其中腐蚀是造成管道穿孔的主要因素。 为保证管道的安全运行， 需要对腐蚀管道的剩余强度进行计算和评价

。 国外学者对管道剩余强度的研究较早， Kiefner 基于断裂力学提出了NG-18 计算公式， 并采用水压爆破试验进行修正， 但计算精度较差

； ASME 在此基础上通过修正缺陷投影面积、 流变应力和当量长度系数等， 提出了ASME B31G 公式， 最新版本为2009，但该公式主要适用于X52 钢级以下的中低强度钢

；挪威船级社提出了DNV-RP-F101 计算方法， 该公式适用于X80 钢级以下的钢材； 美国Battle 实验室提出了PRORRC 计算方法， 该公式适用于X52～X70 中高强度钢； Xu

、 Wang

等人通过有限元分析， 依据Von Mises 等效应力准则计算剩余强度， 计算方法较为准确， 但有限元分析需建模、网格划分等步骤， 操作过于繁琐。 因此， 尽管以上方法对于评价管道剩余强度具有一定作用， 但计算结果趋于保守且无法完全适用不同强度的钢材， 而有限元分析步骤过于繁琐， 易在制定管道运行策略时过早采取降压运行或换管使用。 基于此， 在人工智能、 机器学习的环境下， 通过广义回归神经网络 （GRNN） 对腐蚀管道剩余强度进行有效预测， 采用改进的布谷鸟搜索算法（ICS）对光滑因子进行寻优， 建立基于ICS-GRNN 的管道剩余强度预测模型， 并与其他模型进行对比，验证预测结果的可靠性， 以期为确定腐蚀管道服役寿命和服役状态提供参考。

840 Digital whole slide helps artificial intelligence in pathological imaging strategies

1 基于ICS-GRNN 的管道模型

1.1 GRNN

GRNN 是由美国学者Specht 提出的基于非线性回归理论的前馈型神经网络， 属于径向基神经网络的一个分支。 GRNN 以样本数据为后验条件， 通过执行Parzen 非参数估计， 参照最大概率原则进行网络输出， 具有训练速度快、 全局收敛快、 非线性逼近能力强等特点， 在结构上分为输入层、 模式层、 求和层和输出层。

（1） 输入层： 输入层神经元的个数与输入样本的向量维数M 相等， 神经元将输入样本通过线性函数传递给模式层。

（2） 模式层： 模式层神经元的个数与输入样本的数量n 相等， 各神经元对应不同的样本， 第i 个神经元的传递函数P

为

（4） 输出层： 该层神经元的个数与输出样本的向量维数k 相等， 将两类求和层的神经元相除得到输出层神经元的输出为

经研究表明， 影响腐蚀管道剩余强度的因素主要是管材和缺陷特征。 其中管材特征包括钢级、 管径、 壁厚、 屈服强度、 抗拉强度； 缺陷特征包括缺陷形状、 缺陷长度、 缺陷宽度和缺陷深度。 在其他条件一致的情况下， 管道钢级越高，剩余强度越大。 管径越大， 剩余强度越小； 壁厚越大， 剩余强度越大； 屈服强度和抗拉强度对管道剩余强度的影响结果基本一致， 两者均通过流变应力影响剩余强度。 通常情况下， 钢级越高，屈服强度和抗拉强度就越大， 剩余强度也越大。常见的腐蚀缺陷形状有矩形、 圆形、 槽形和不规则形状， 不同形状的缺陷尺寸有所不同。 缺陷长度、 缺陷宽度和缺陷深度与剩余强度呈负相关，其中缺陷深度对剩余强度的影响最大， 而缺陷宽度的影响最小。

Levy （λ） ——Levy 随机搜索方式。采用Levy 飞行机制， 其行走步长满足重尾的稳定分布。 基本算法是按照公式 （5） 对寄生巢位置进行更新， 并计算目标函数适应度， 如该值优于上一次的目标值， 则更新鸟巢位置； 位置更新后， 采用随机生成的数值与P

比较， 并对鸟巢位置进行随机更改； 最后， 保留适应度最好的鸟巢位置， 结束迭代过程， 输出全局最优值。

1.2 布谷鸟搜索算法（ICS）

显然，除了履行工商经济类、公益慈善类、社会福利类、社会服务类这“四大类”职能的社会组织，其他类别的社会组织就难以得到此优待。总体上看来，民办非企业单位很多都属于这些类别关照的范围；尽管如此，在现实当中，属于“四大类”的社会组织也有不少在登记管理环节依然面临着棘手难题；例如对人数和办公场所的限制，很多规模有限、资源紧张的组织可能依然达不到登记门槛的要求。而且，面临这一问题的组织还不在少数。也就是说，文件规定的门槛虽然在降低，但是离大部分民办非企业单位的实际需求仍有一定距离。

⊗——点对点乘积；

式中： a——步长控制量；

回屋后，我到灶膛刮了半瓢锅底灰，抓一把捂在桂生还在滴血的耳朵上，扯了块儿棉布把他半个脸都包起了。大梁把瓢接过去，锅底灰刚撒上阿黄的伤口，很快就被鲜血洇湿了。我把桂生料理困了，就来陪阿黄。它躺在我的脚边，眼睛闭着，一个劲儿打寒战。到后半夜，阿黄冇打寒战了，只是隔一刻就抽搐一下。它终究还是冇能熬到天明！五更天鸡叫头遍，我看到阿黄好久都冇动静，摸了摸它的身子，冰冰凉的——可怜的阿黄，就这样无声无息地，匆匆走完了它短暂又卑微的一生！

传统的CS 算法中a 值取1， P

取固定值，易陷入局部最优解。 为加强算法的局部搜索和自适应能力， 引入反余弦函数对CS 算法进行改进， 形成ICS 算法， 公式如下

达瑞矿业(PT Dairi Prima Mineral)是布密资源的全资子公司，其主要资产是印尼达瑞铅锌矿。股权交割完成后，中色股份持有达瑞矿业51%的股份。

1.3 ICS-GRNN 的管道剩余强度预测模型

将样本数据按照80%和20%的比例分为训练集和测试集， 将训练集进行归一化处理后输入GRNN 进行预测， 选择平均相对变动值 （ARV）为适应度函数， 采用ICS 算法对光滑因子寻优，通过不断更新GRNN 的权值和阈值， 得到最优GRNN 模型， 将测试集代入优化模型， 输出预测值， 分析验证结果的准确性和可行性， 预测流程如图1 所示。 适应度函数为

以上两个指标值越小， 模型的预测精度越高， 当MAPE 值高于5%时， 说明预测结果不可靠； Theil IC 数值在0～1 之间， 数值越小代表模型的鲁棒性越好。

2 实例应用

2.1 指标体系构建与数据来源

在GRNN 回归的过程中， 只需要确定一个超参数δ。 目前， δ 的选取主要依靠人工试算，随意性较强， 在此采用ICS 算法对其进行寻优。

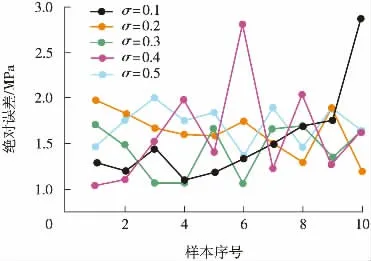
采用Matlab 对模型进行编程， 将非数字型的数据转化为数字型， 如将X42 钢级定义为1，X46 钢级定义为2， 依次类推； 同理， 将缺陷形状中的矩形定义为1， 圆形定义为2， 槽型定义为3， 不规则形状定义为4。 随机抽取10 组数据，分别定义光滑因子δ 为0.1、 0.2、 0.3、 0.4 和0.5，GRNN 的模型结构为（8， 10， 10， 1）， 预测结果的绝对误差如图2 所示。 通过图2 可以看出GRNN 的预测结果并不稳定， δ 的取值对其影响较大， 因此需要采用ICS 算法对δ 进行寻优。

为提高预测效果的准确性， 选择真实的水压爆破试验数据， 从文献[8-12]中选取79 组数据，该数据涵盖了钢级在X42～X100 范围内所有常见的管道类型， 将数据分为两组， 64 组为训练集，15 组为测试集。

布谷鸟搜索算法 （ICS） 源于布谷鸟的繁育行为， 属于新兴启发算法。 假设布谷鸟的产卵行为满足以下三个理想状态： ①布谷鸟每次只产一个卵， 并随机选择寄生巢来孵化它； ②随机选择一组寄生巢， 并将最好的寄生巢保留至下一代；③寄生巢的数量是固定的， 当寄主发现外来鸟蛋后， 寄主可选择消灭该蛋或抛弃该寄生巢。 设布谷鸟蛋被寄主发现的概率为P

= [0， 1]， 第z 个寄生巢在第t 次迭代中的位置为x

， 则第t+1 次迭代的更新方式为

2.2 剩余强度预测结果

综上所述， 选择管道钢级、 管径、 壁厚、 屈服强度、 缺陷形状、 缺陷长度、 缺陷宽度和缺陷深度等8 个因素作为剩余强度的主要影响因素，因抗拉强度与管道钢级和屈服强度相关性较大，故予以剔除。

（2）涔天河水库扩建工程的建设符合国家产业政策，符合地方的发展规划，工程建设具有较大的经济效益、社会效益。库区的建设为当地农民脱贫致富创造条件。水库扩建通过移民开发式扶贫，移民生活水平能得到恢复并有所提高，解决了库区近3万农民脱贫致富问题，经济社会效益显著[6]。

设置ICS 算法的P

和P

分别为0.1、 0.5，a

和a

分别为0.5、 1， 种群个数为50， 最大迭代次数为200 次。 为验证ICS 算法的优越性， 将其与标准的CS 算法进行对比， 设置P

为0.5、 a 为1 时， ICS 和CS 算法的迭代结果如图3 所示。 随着迭代次数的增加， ICS 的迭代速度更快， 整体误差和波动与CS 算法相比更小， 采用ICS 算法迭代47 次后达到收敛条件， 此时δ 取值为0.647 5，而采用CS 算法在迭代135 次后达到收敛条件，因此ICS 算法较CS 算法提前了88 次。

在译介的俄苏文学中，有不少关于俄苏战争题材的文学作品及论文，其中颂扬社会主义革命及传递战斗精神是主流。这对战时响应时代要求及在国统区传播社会主义思想意义重大。细读战时文学期刊上刊发的重要文章，可概括为以下两方面的内容。

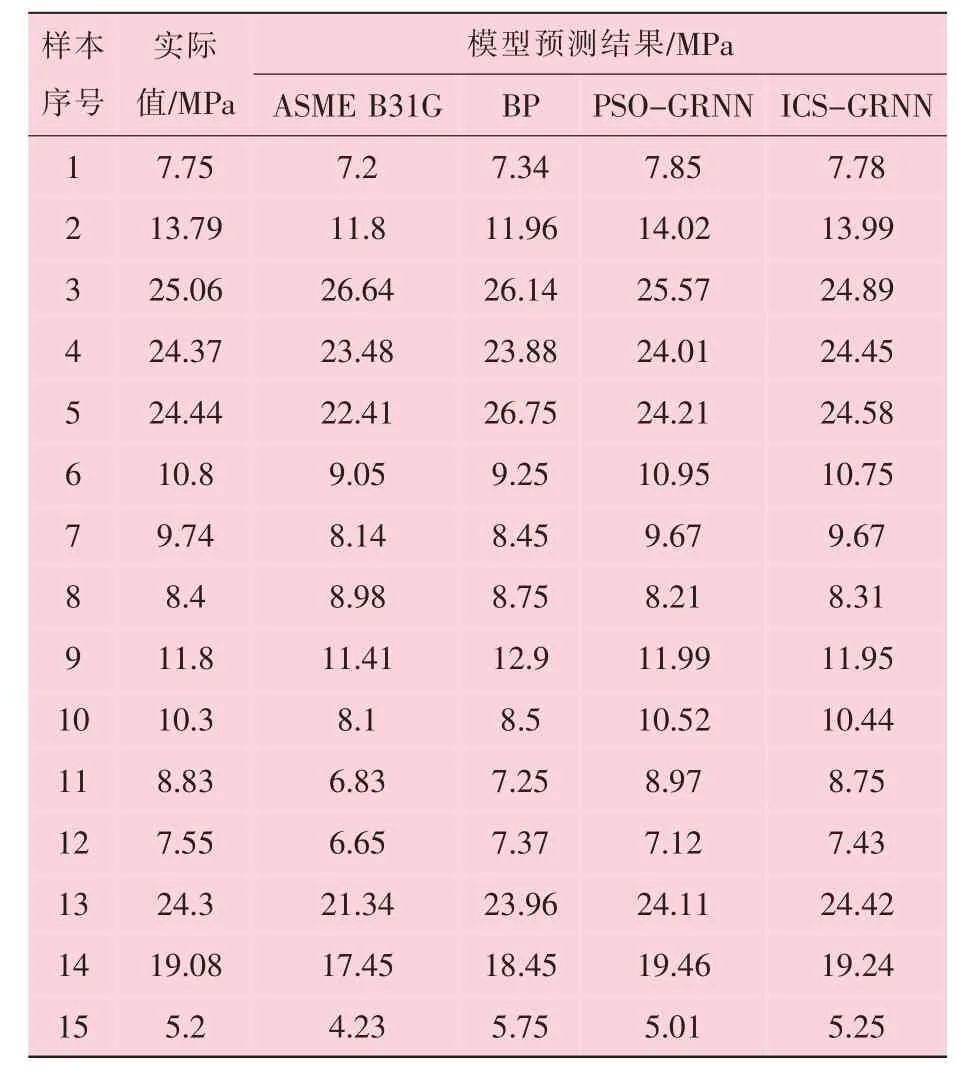
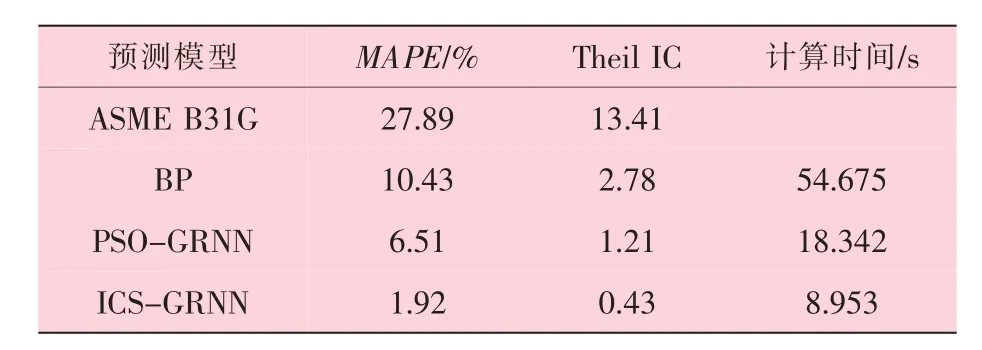
为分析ICS-GRNN 模型的准确性， 将预测结果进行反归一化处理， 并与ASME B31G、BP 模型、 PSO-GRNN 模型的计算结果进行对比， 各类模型的预测结果如图4 所示， 预测数值见表1， 残差如图5 所示， 模型性能评价见表2。 分析发现， 大部分ASME B31G 的评价结果均比真实值小， 且残差波动最大， 说明ASME B31G 的评价结果存在一定保守性， 如按照该结果指导生产， 会过早地更换管道； 其他三种模型中， ICS-GRNN 模型预测结果的残差波动最小， 基本在0 值附近波动， 而BP 模型、PSO-GRNN 模型的残差波动较大， 说明ICSGRNN 模型的预测精度和鲁棒性较好。 从表2可知， ICS-GRNN 模型的平均相对误差和希尔不等系数均最小， 分别为1.92%和0.43， 与BP模型相比， GRNN 模型属于连续函数的最佳逼近， 可以以任意精度逼近任意非线性函数， 而BP 模型因采用的Sigmoid 激活函数具有全局特性， 输入样本在很大范围内对输出样本产生影响， 导致BP 模型的训练效果较差， 同时训练时间较长； 与PSO-GRNN 比较， ICS 算法对光滑因子的寻优效果更好， 迭代速度更快。

3 结 论

（1） 利用反余弦函数优化后的ICS 算法比CS算法的迭代速度更快， 整体误差更小， 可更快更好地对光滑因子进行寻优。

（2） ICS-GRNN 模型的平均相对误差和希尔不等系数均最小， 分别为1.92%和0.43， 与其他模型相比， 预测精度和鲁棒性最好， 预测时间最短。

[1] 柴强飞，肖忠东，高竟喆，等. 基于尖锥网络分析法的管道风险评价研究[J]. 中国安全科学学报，2017，27（7）：88-93.

[2] 骆正山，袁宏伟.基于误差补偿的GM-RBF 海底管道腐蚀预测模型[J]. 中国安全科学学报，2018，28（3）：96-101.

[3] 陈兆雄，吴明，谢飞，等. 腐蚀管道剩余强度的评价方法及剩余寿命预测[J]. 机械工程材料，2015，39（5）：97-101.

[4] MA B，SHUAI J，WANG J，et al. Analysis on the latest assessment criteria of ASME B31G—2009 for the remaining strength of corroded pipelines [J]. Journal of Failure Analysis& Prevention，2011，11（6）：666-671.

[5] 马彬，帅健，李晓魁，等. 新版ASME B31G—2009 管道剩余强度评价标准先进性分析[J]. 天然气工业，2011，31（8）：112-115.

[6] XU L Y，CHENG Y F. Reliability and failure pressure prediction of various grades of pipeline steel in the presence of corrosion defects and pre-strain[J].International Journal of Pressure Vessels&Piping，2012，89（1）：75-84.

[7] WANG N，ZARGHAMEE M S. Evaluating Fitness for Service of Corroded Metal Pipelines：Structural Reliability Bases[J].Journal of Pipeline Systems Engineering&Practice，2014，5（1）：1-9.

[8] MA B，SHUAI J，LIU D，et al. Assessment on failure pressure of high strength pipeline with corrosion defects[J].Engineering Failure Analysis，2013，32（9）：209-219.

[9] FREIRE J L F，VIEURA R D，CASTRO J T P，et al.PART 3：Burst Tests of Pipeline With Extensive Longitudinal Metal Loss[J]. Experimental Techniques，2006，30（6）：60-65.

[10] CRONIN D S，PICK R J. Experimental database for corroded pipe：Evaluation of RSTRENG and B31G[C]//International Pipeline Conference. Calgary，Canada：IPC，2010.

[11] BENJAMIN A C，VIEIRA R D，FREIRE J L F，et al.Burst tests on pipeline with long external corrosion [C]//International Pipeline Conference. Calgary，Canada：IPC，2010.

[12] SOUZA R D，BENJAMIN A C，VIEIRA R D，et al. PART 4：Rupture tests of pipeline segments containing long real corrosion defects [J].Experimental Techniques，2007，31（1）：46-51.