关于MLCC加速寿命试验加速指数的研究

黄翔，敖宏，宋进祥，邓积吉

（广东微容电子科技有限公司，广东 云浮 527200）

0 引言

多层片式陶瓷电容器（MLCC：Multiplayer Ceramic Chip Capacitors）作为电子设备中不可或缺的组件，被广泛地应用于隔直、耦合、旁路、滤波、调谐回路、能量转换和控制电路等方面。随着技术的升级，不同的应用场合对MLCC的可靠性提出了更高的要求[1]。在消费电子领域一般要求MLCC具有5年以上的使用寿命，工业级应用领域要求具有10年以上的寿命，而车载应用领域甚至需要达到15年的寿命。

MLCC制造商一般使用1 000 h的耐久性指标来描述电容器能达到的基本可靠性水平。为了对标不同领域下的使用要求，需要进行额外的试验来模拟电容器在实际使用中的失效率及其可能达到的寿命。然而，更长周期的试验所耗费的时间和人工成本巨大，MLCC制造商往往通过加速寿命试验来推算其在正常使用条件下的寿命特征和失效率[2-3]。目前，加速寿命试验已经被广泛地应用于通讯、电子、能源和汽车等领域，它可以解决高可靠、长寿命产品的可靠性增长、评估问题，也可以缩短产品的研发周期，节约产品的研发成本，让产品在市场竞争中抢占先机。

加速寿命试验是在不改变失效机理的条件下加大应力进行的试验。它选择比正常使用环境更加恶劣的应力水平来加快产品失效以缩短试验时间，在获得的失效数据的基础上运用加速模型对产品在正常应力条件下的各种寿命特征进行统计推断[4-5]。在MLCC领域，常用的加速应力为温度和电压，所以加速试验一般是通过提升试验温度和提高施加电压来进行的[6-7]。加速寿命试验的准确性取决于加速模型的合理性，因此，估算加速模型中的加速因子成为各大MLCC制造商亟需解决的问题。本文通过研究不同的温度应力和电压应力下MLCC的失效情况，拟合计算得到相应的加速因子，进而可预测相同的材料体系下MLCC的使用寿命及失效率分布情况。

1 实验

选取已经过筛测后的0402-475规格的MLCC产品进行加速试验，加速试验的温度应力取3个：105、125和140℃；试验的电压应力为：50.4、47.2、44.1、40.9、37.8、34.6、31.5和25.2 V。样品数量为56 pcs。

2 结果分析

将各种试验条件下的漏电流随时间的变化情况以曲线形式表示，以105℃为例，结果如图1所示。电容在试验过程中，随着试验的进行，漏电流先缓慢地上升，到达某一时间点后，样品内部通过的电流急剧地升高，然后稳定在一个高电流水平处。样品失效时间点的判定为电流急速升高所对应的时间，在相同的温度下，随着施加电压的降低，样品的失效时间逐渐地增大。

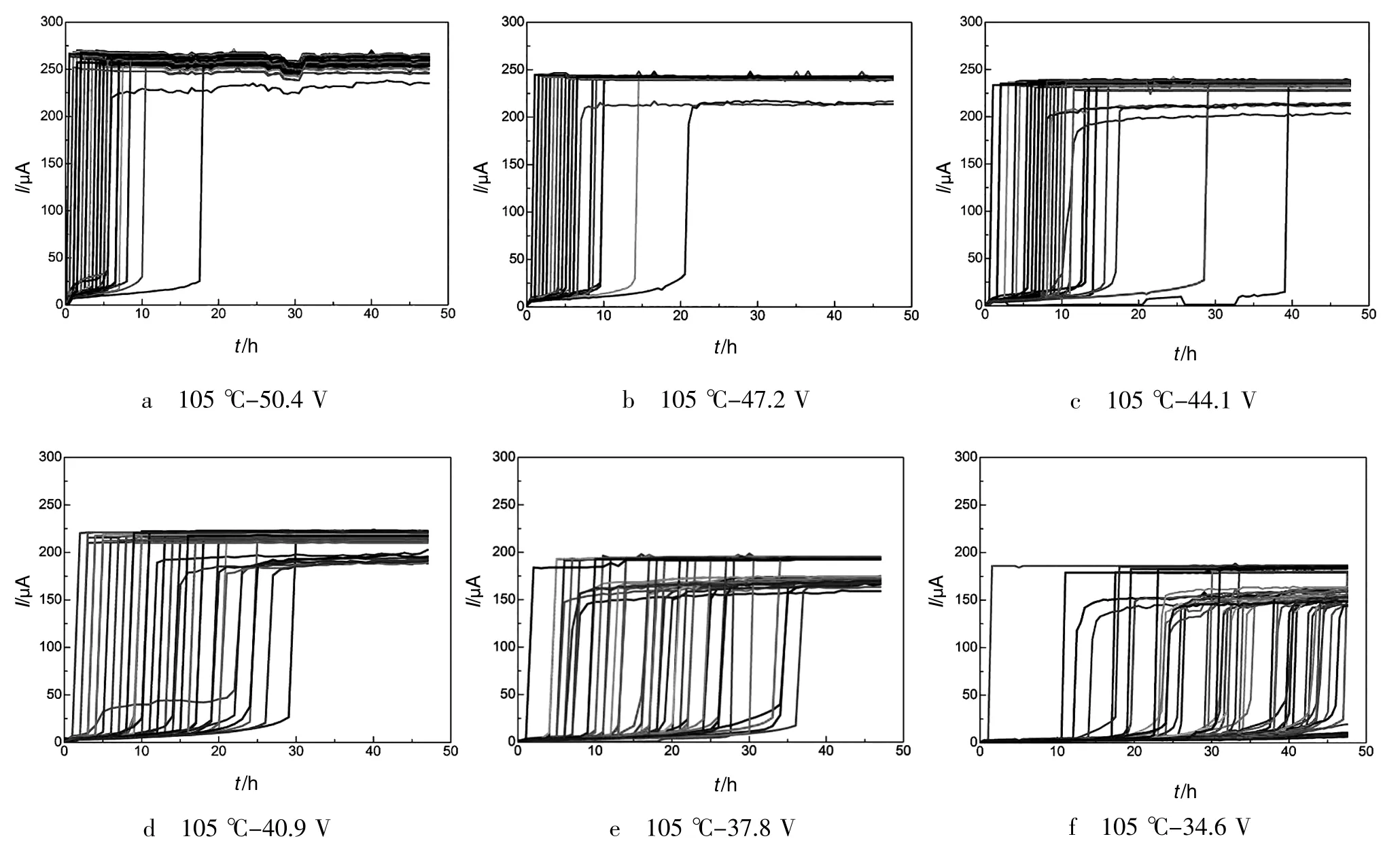
图1 105℃下电容在不同电压下的漏电流曲线

将上述的失效时间记录下来，就形成了特定温度下的失效分布。电容器的失效分布使用最广的是双参数的Weibull模型，它在可靠性理论中被广泛地使用，大多数电子、机械和机电产品的寿命都可以认为服从Weibull分布[8-9]。利用它描述电子设备的寿命和维修时间，可以更全面地分析早期故障、偶然故障和耗损故障3个阶段的系统可靠性。公式如下：

式（3）中：β——无量纲的形状参数，其值通常是特定的故障模式下的特征研究，可以反映失效的机理；

η——特征时间尺度参数，与所有的其他相关特征时间有关，如平均故障时间（MTTF）。

在进行加速模型的研究过程中，要求失效分布必须代表相同的失效机理，以保证外推正常工作条件下寿命的准确性和可信性，也就是Weibull分布中的形状参数β需要相近[10]。对Weibull分布公式进行变换可以得到：

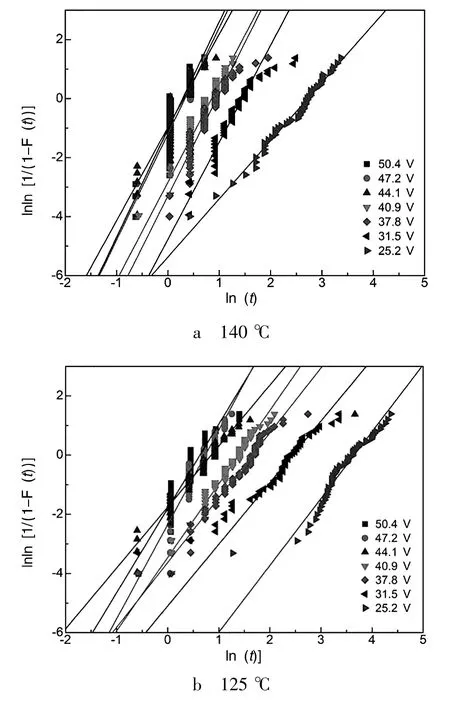
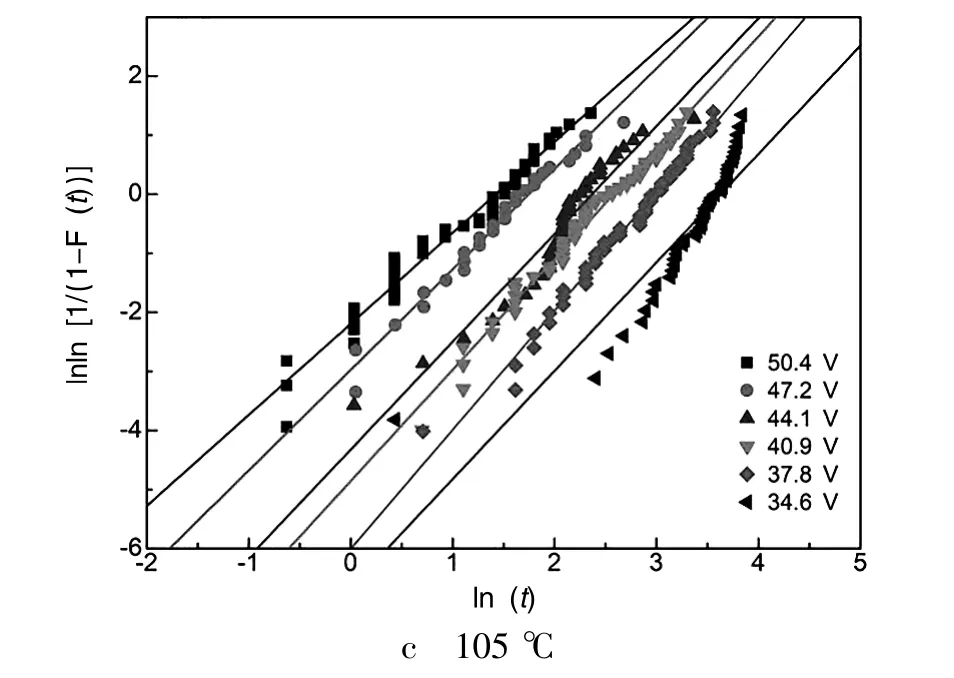
图2 基于Weibull分布的失效率拟合

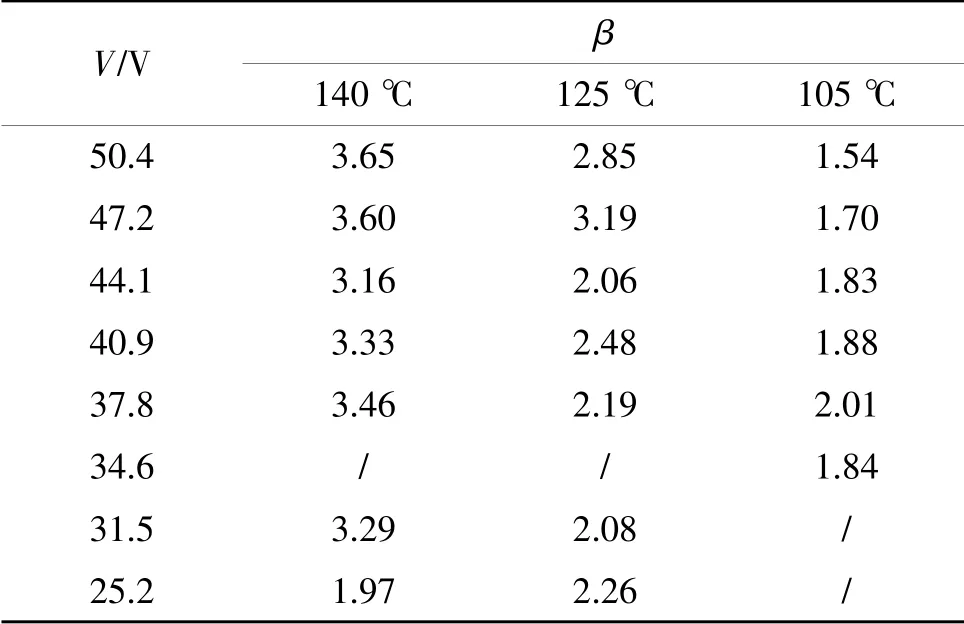
表1 形状参数β的拟合结果

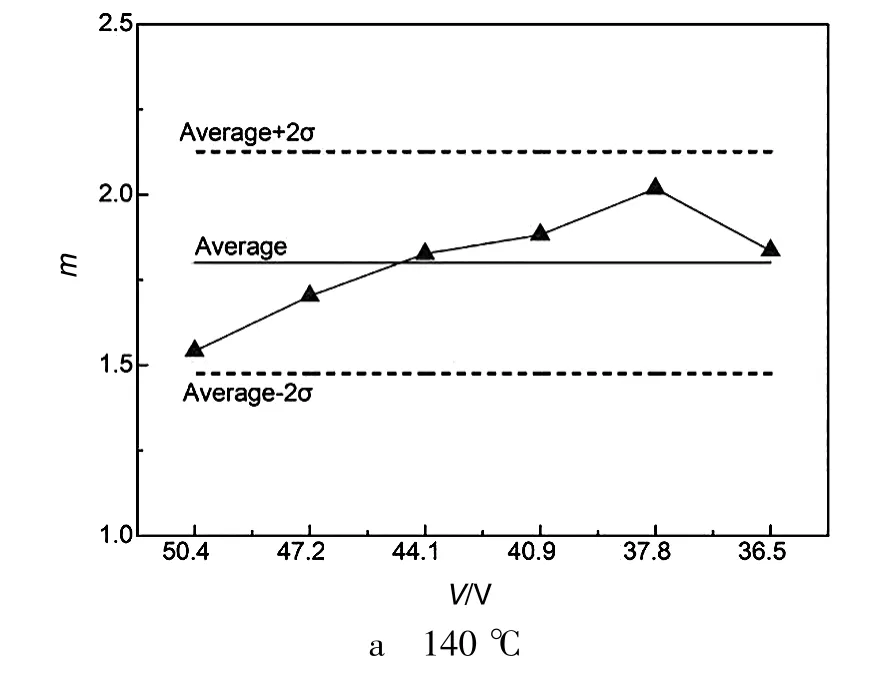
为了保证不同电压下的失效分布具有相同的失效机理，需要对形状参数β进行异常点的判别和剔除。以下采用拉依达准则（也就是3σ准则）进行异常数据的判定，因数据点较少，3σ范围的精度无法达到，此处使用2σ范围进行识别，相当于显著性水平α=0.05。3个温度点下，不同的电压下失效分布的β参数的异常数据判定图如图3所示。从图3中可以看出，140℃下25.2 V时的β参数存在显著异常，表明其失效分布机理与其他电压条件时不一致，该数据予以剔除，不在后续的拟合中使用。

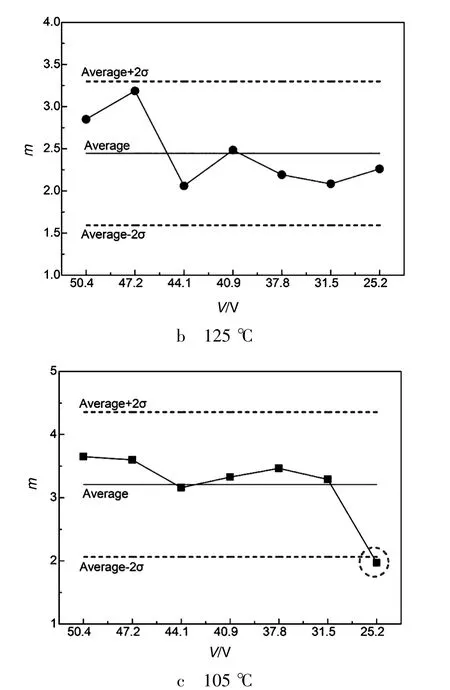
图3 形状参数β的异常判定

在上述加速试验条件下，样品并非在同一时间失效，这里采用56颗样品的平均失效时间来衡量在该试验条件下的样品寿命，如表2所示。从表2中可以看出，样品平均失效时间随着测试电压的降低而增大，随着测试温度的降低而增大。

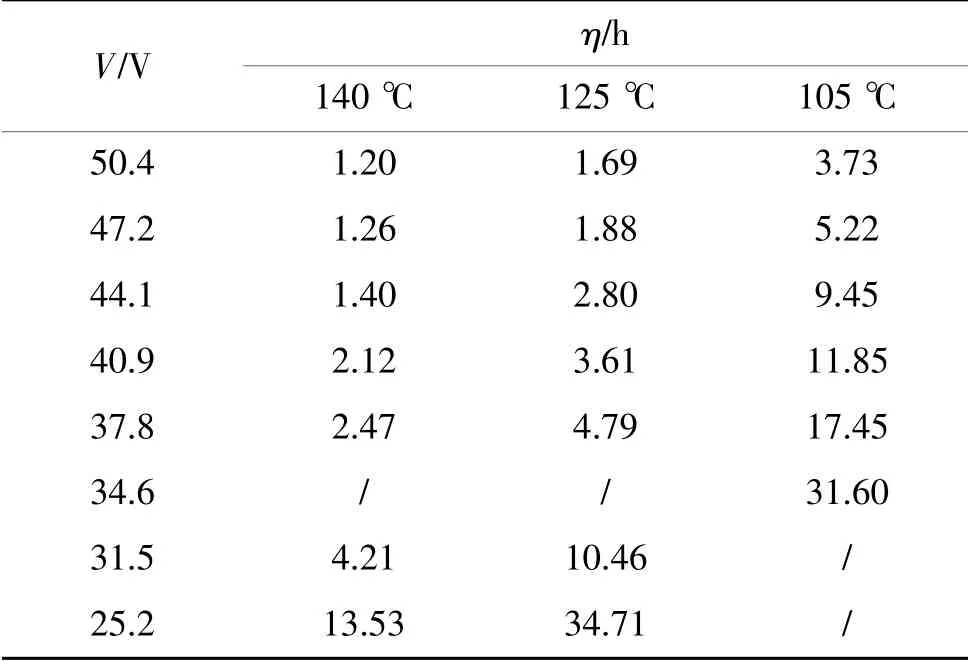
表2 加速试验的平均失效时间

在上述试验中，样品受到两种加速应力的作用，一种是温度，另一种是电压。温度应力和电压应力的作用机制都是加速电子的迁移，从而促使样品快速地失效。但这两种应力的加速程度不同，温度加速符合Arrhenius模型，而电压加速一般更接近逆幂律模型，具体可由以下经验公式表示[11-13]：

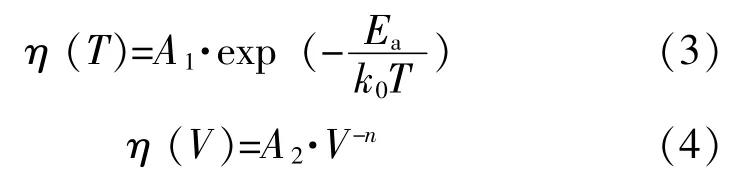
式（3）-（4）中：η——失效时间参数；

A1、A2——常数；

Ea——激活能，与样品材料属性有关；

k0——Boltzmann常数，取值为1.38×10-23J/K；

T——试验温度；

V——试验电压；

n——电压加速指数。

因此，针对MLCC的失效模型，一般采用上面两种的组合得到，可以表示为：

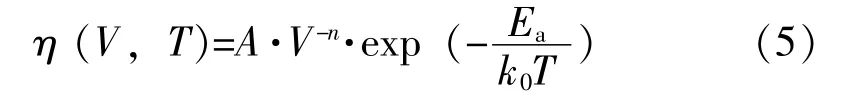
对于激活能Ea，因其与材料属性相关，在BME-MLCC中，其数值一般在0.9～1.7 eV之间，其中最常用的是1.1 eV。而电压加速指数n可以采用相同温度下不同电压的加速试验计算得到，且它在不同的温度下也具有不同的数值。对公式（4）取对数变换得到：

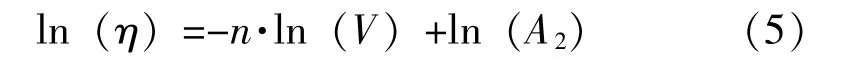
采用线性拟合可以得到不同温度下的电压加速指数n，如图4所示。最终结果为：140℃下，n值为3.74；125℃下，n值为4.37；105℃下，n值为5.54。电压加速指数随温度降低而呈现增大的趋势，可以理解为在较低的温度应力下，MLCC产品对电压加速更敏感；而随着温度的升高，温度的加速效应逐渐地上升，电压加速效应将弱化，导致电压加速指数降低。也就是表明在MLCC中，温度应力和电压应力的合应力处于一种平衡状态。

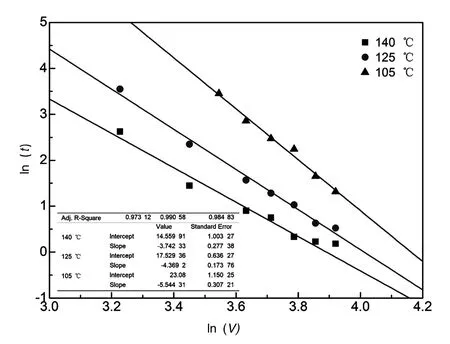
图4 电压加速指数n的拟合计算

利用上面得到的电压加速指数n和Ea经验值，在失效机制没有发生改变的前提下，可以估算在任一试验条件下的失效时间，从而可以评估比较正常应力条件下的各种寿命特征，这对于MLCC产品的开发意义重大。

3 结束语

本文系统地研究了MLCC样品的加速寿命试验，采用不同的温度加速和电压加速条件，得到样品的失效分布状况，根据Weibull分布模型判断加速条件的失效机制是否一致，利用形状参数的变异排除掉异常点。最后，计算各个加速试验的失效时间，根据经验公式计算电压加速指数，最终结果对于MLCC寿命评估起到一定的参考和借鉴作用。