直线翼垂直轴风力机气动特性的数值分析

周晖钰，郭志平*，张艳锋，宋晓文

(1. 内蒙古工业大学机械工程学院，内蒙古 呼和浩特 010051；2. 内蒙古工业大学理学院，内蒙古 呼和浩特 010051)

1 引言

随着全球能源危机和环境污染日益突出，风能技术这种可利用的再生清洁能源技术已成为世界各政府面对100以上问题所采取的重要手段。经过几百年的发展，如今风力机依据其旋转轴方向的不同分为：水平轴风力机(Horizontal Axis Wind Turbines，HAWT)和垂直轴风力机(Vertical Axis Wind Turbines，VAWT)[1，2]。直线翼垂直轴风力机(Straight-bladed Vertical Axis Wind Turbines，Sb-VAWT)属于VAWT的一种类型，其具有制造简单、成本较低、启动风速低等特点[3]，且不同于HAWT需要复杂的偏航装置，Sb-VAWT无需偏航装置，发电机可安装在近地面，便于维修和保养。综合以上优势，Sb-VAWT可被应用在经济不发达的山区、草原和海岛[4]或者城市照明、应急指示设备、救援设备的充电电源。然而Sb-VAWT的研究相对于HAWT起步较晚，且技术不成熟。因此开展对Sb-VAWT的应用研究，对乡村、牧区、海岛和城市用电的补充和完善具有重要意义。

2016年日本三重大学的LI Qing-an等人利用风洞试验与CFD数值分析相结合的方法研究了Sb-VAWT的流场特性和功率特性[5，6]，得出叶片翼展中心的气动性能较好，Sb-VAWT的功率系数主要在上流域取得，在2017年通过风洞实验与外场测试，研究了湍流强度对垂直轴风力机的影响，得出在湍流强度较高的情况下，低叶尖速比功率系数的外场试验结果要比风洞试验的结果高[7]。同年内蒙古工业大学的YANG Yan-zhao等人对不同尖速比下双叶片Sb-VAWT的叶尖涡进行了数值研究[8]，得出在低尖速比时叶尖涡结构沿叶片展向分布更为复杂，在高尖速比时叶尖涡耗散距离较长，在2018年利用CFD数值分析结合实验的方法研究了不同安装角对双叶片Sb-VAWT气动特性的影响，得出了双叶片Sb-VAWT在安装角β=6°时，气动特性最好[9]。采用数值模拟的方法可以在一定程度上计算和分析不同尖速比下Sb-VAWT的气动特性，具有相对简单、成本低、时间短的特点，是当前研究Sb-VAWT重要手段[10]。

综上所述，尖速比能通过直接影响Sb-VAWT叶片周围流场进而改变叶片表面的压力分布，从而导致叶片升阻比和风力机功率系数的变化。本文将基于CFD数值分析法对不同尖速比下Sb-VAWT的气动特性进行分析。

2 运动模型和CFD数值模拟法

Sb-VAWT的各类参数对其性能有很大的影响，各个参数之间相互联系且影响复杂。为了研究不同尖速比对Sb-VAWT气动特性和功率系数的影响，需要定义其运动模型，运动模型包含叶片部分的速度、几何角度和受力状况。

2.1 运动模型

如图1和图2所示，虚线为Sb-VAWT的叶片气动中心的旋转迹线。x轴方向水平向右，y轴方向竖直向上。来流方向与x轴方向一致且流速为U0。从风力机顶部看转子的旋转方向为顺时针方向且角速度为ω，方位角为θ，沿y轴负方向θ为0°且沿顺时针方向旋转为正。V(V=Rω)为叶片转速，V与叶片弦线方向的夹角为安装角β，逆时针方向为正。W为合成速度，其与弦线方向的夹角为攻角α，逆时针方向为正，W为合成速度和攻角α可表示为

W=V-U0

(1)

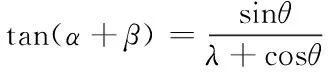
(2)

其中λ为风力机尖速比λ，可表示为

(3)

由图2可知，切向力FT方向沿叶片速度的切向方向，可表示为

FT=FLsinφ-FDcosφ

(4)

其中FL为叶片升力，其方向垂直于叶片弦线方向并指向旋转中心。FD为叶片的阻力，其方向与叶片弦方向平行。φ是合成速度W与切向力FT之间的夹角，可表示为

φ=α+β

(5)

单叶片转矩Q是由叶片的切向力FT产生的，因此单叶片转矩Q可以用切向力FT表示为

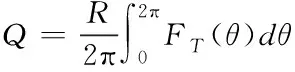
(6)

其中R为风力机旋转半径，对转矩Q进行无量纲化后得到的单叶片转矩系数为

(7)

其中ρ为空气密度，D为风力机旋转直径，H为风力机叶片展长。根据所得的转矩系数可得单叶片功率系数为

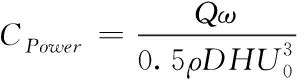
(8)

P为作用在叶片表面的压力，它垂直于叶片表面。为方便计算对其进行无量纲化，定义作用于叶片表面的压力系数CP为

(9)

综合以上公式可知，功率系数代表了风力机的气动效率。

图1 速度和几何角定义

图2 受力分析

2.2 CFD数值模拟法

2.2.1 Sb-VAWT三维模型

针对文献[11]中翼型为NACA0021的三叶片Sb-VAWT建立三维模型。由于支撑杆、塔架等对风轮流场影响较小，所以简化为只含叶片和旋转轴的风力机模型[12-14]，如图3所示，其基本参数见表1。

图3 Sb-VAWT三维模型示意图

表1 Sb-VAWT基本参数

2.2.2 Sb-VAWT计算域和网格

图4 计算域和边界条件设置示意图

利用ICEM CFD软件对三维模型计算域和边界条件设置如图4所示。计算域分为静止域、旋转域和叶片域。其中静止域长40m、宽20m、高2.4m，左端边界面设置为速度入口(InletVelocity)，右端段边界面设置为压力出口(Outlet Pressure)，与旋转域和叶片域接合面均为交界面(Interface)，其余边界面为对称面(Symmetry)；图5为旋转域和叶片域，其中旋转域直径3m、高1.2m，除旋转轴面设置为边界面(Wall)，其余各面均设置为交界面(Interface)；叶片域直径600mm、高1.2m，除叶片面设置为边界面(Wall)外，其余各面均设置为交界面(Interface)。

图5 旋转域和叶片域示意图

为了准确得到作用在叶片表面的压力分布，需要对叶片附近的边界层进行加密，网格从叶片表面沿法线方向以1：1.1的比例增长，边界层第一层网格高度为y=0.02mm，如图6所示。

图6 叶片边界层网格

2.2.3 Sb-VAWT求解器设置

CFD数值分析采用滑移网格技术，选择k-ωSST湍流模型和SAMPLE迭代算法进行数值计算。依据文献[9]，k-ωSST湍流模型结合了k-ω湍流模型和标准k-ε湍流模型的优点，修改了湍流粘度公式，使其考虑了湍流剪切应力的影响，并且对网格质量要求较低，常用于风力机的研究。

利用ANSYS Fluent软件计算了不同尖速比下的单叶片瞬时转矩、压力分布。所计算的尖速比为λ=0.6、1.2、1.4、1.8、2.2、2.6。湍流强度IT=5%，并对单叶片瞬时转矩进行监控，图7为尖速比λ=1.8时的单叶片转矩监测曲线图。由图7可知当t>1.5s时曲线开始有规则波动，说明此时CFD数值仿真开始收敛。

图7 单叶片转矩监测曲线图

2.2.4 数值模拟验证

为了验证数值模拟的可靠性，当湍流强度IT=5%、来流风速U0=8 m/s、尖速比λ=1.8时，进行数值仿真，得到的Sb-VAWT单叶片转矩系数曲线与文献[15]中的实验数据进行比较，如图8所示，在30°<θ<240°之间，数值仿真数据与实验数据趋势相同，但数值仿真数据稍大于实验数据，是因为实验过程中机械结构存在摩擦损耗，所以实验数据数值相对较小；在240°<θ<30°之间，数值仿真结果与实验结果相差较大，这是由于垂直轴风力机在上流域形成的尾流对下流域影响较大，而实验所用的垂直轴风力机存在叶片支撑架使得实验中垂直轴风力机尾流场更加复杂，而数值仿真简化去掉了片支撑架。Sb-VAWT的功率系数主要在上流域取得，而数值仿真数据与实验数据在上流域趋势相同，可证明本次数值仿真具有一定的可靠性。

图8 单叶片转矩系数曲线

3 气动特性分析

3.1 总转矩系数和总功率系数

由式(6)、式(7)和式(8)得总转矩系数和总功率系数曲线，如图9所示。

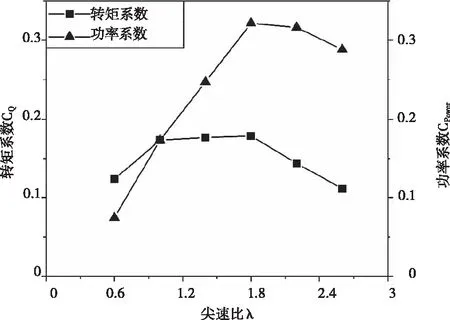
图9 转矩系数和功率系数曲线

由图9可知，转矩系数和功率系数随着尖速比的增大而增大，当尖速比λ=1.8时，取得最大值，分别为0.179(转矩系数)和0.322(功率系数)随后随着尖速比的增加，两系数随之皆下降。由此可知三叶片Sb-VAWT的最佳尖速比为λ=1.8。

3.2 单叶片转矩系数和功率系数

为了便于分析和计算，取低尖速比λ=1.4、最佳尖速比λ=1.8和高尖速比λ=2.2三组数据对单叶片的转矩系数和功率系数进行分析，如图10和图11所示。

在图10中，叶片经过上流域(0°<θ<180°)时，转矩系数随着方位角θ的增加而增加，在θ=90°附近取得最大值，分别为：0.325(λ=1.0)、0.317(λ=1.8)和0.248(λ=2.6)，此后随着方位角θ的增加而减少直到θ=180°附近时降低到0。叶片经过下流域(180°<θ<360°)时，转矩系数曲线变化相对平缓。造成这一现象的原因是叶片攻角α受方位角的影响，由式(2)可得到低尖速比λ=1.4、最佳尖速比λ=1.8和高尖速比λ=2.2的方位角θ与攻角α之间的关系，如图12所示，攻角α在上流域先变大，当方位角θ=90°附近时，叶片攻角α处于失速临界值，此时叶片气动载荷达到最大，随着攻角α的增加，叶片出现动态失速现象，气动载荷随之减小；而在下流域由于受到上流域叶片产生的尾流影响导致来流速度U0降低使得叶片攻角α处于一种平衡状态；随着尖速比的增加，转矩系数峰值反而降低，这是因为尖速比增加导致叶片转速增加，从而造成合成速度W增大，使得叶片攻角α变小。

图10 单叶片转矩系数曲线

由图11可知，单叶片功率系数与转矩系数相似，区别在于，当叶片经过上流域时，随着尖速比的增加，功率系数的最大值也随之增加，其分别为：0.323(λ=1.0)、0.507(λ=1.8)和0.596(λ=2.6)，产生这一现象的原因是功率除了与转矩有关还与转速成正比，当来流风速不变的情况下，转速随着尖速比的增大而增大。

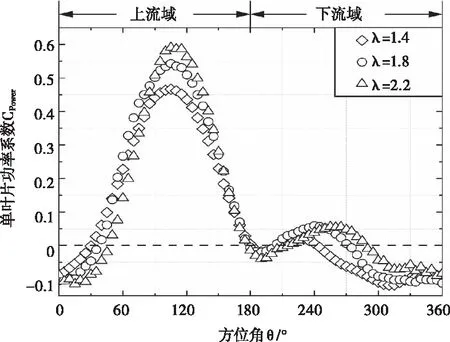
图11 单叶片功率系数曲线

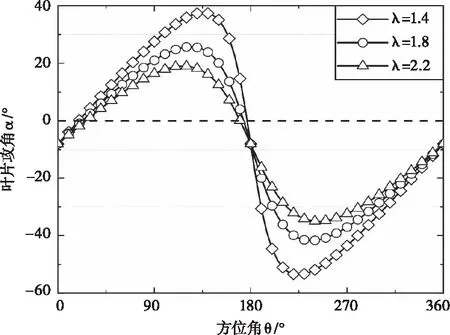
图12 叶片方位角θ与攻角α的关系

综上所述，Sb-VAWT的单叶片转矩系数和功率系数取决于方位角θ，并且在上流域方位角θ=90°附近取得最大值。

3.3 单叶片翼展中心截面压力系数

为了直观分析叶片表面气动载荷分布情况，由文献[5]可知，叶片翼展中心的气动性能较好，取低尖速比λ=1.4、最佳尖速比λ=1.8和高尖速比λ=2.2各自的叶片翼展中心截面压力系数进行分析，其相对应的叶片翼展中心截面压力系数曲线如图13～图15所示。

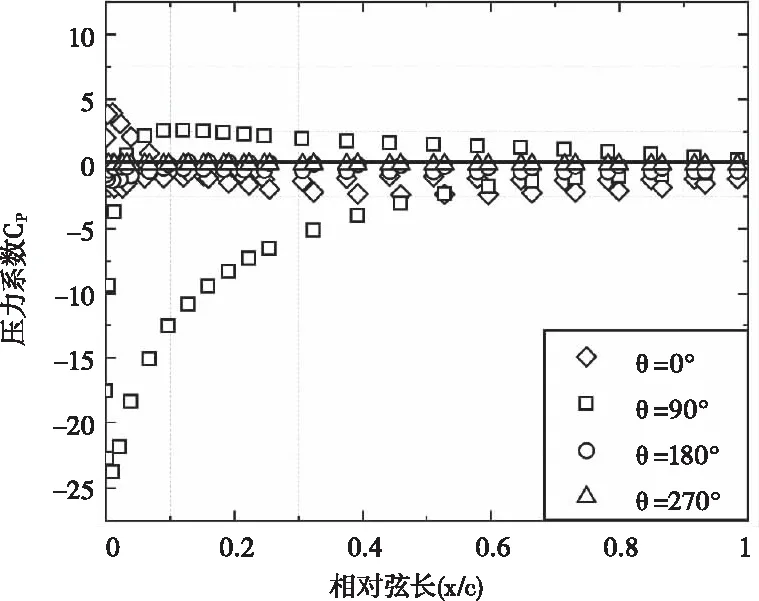
图13 λ=1.4单叶片翼展中心截面压力系数曲线

图14 λ=1.8单叶片翼展中心截面压力系数曲线

图15 λ=2.8单叶片翼展中心截面压力系数曲线

由图14～图16可知，叶片上下翼面压差在翼型前缘最大，并随着弦线方向逐渐减小直到翼型尾缘处趋于0；同时叶片经过上流域且方位角θ=90°时，压力差达到了峰值；这一现象表明叶片经过上流域时，叶片前缘承受了大量的气动载荷，这与之前单叶片转矩系数和功率系数在上流域取得峰值现象相吻合，由此可以推导出，Sb-VAWT发电功率主要取决在上流域叶片前缘的气动载荷分布。相反的是，当叶片经过下流域且方位角θ=270°时，由于叶片在上流域所产生的尾流导致来流速度亏损，使得攻角变小，从而造成叶片前缘压差小于方位角θ=90°时的前缘压差。当叶片旋转到方位角θ=180°时，压差几乎为0，由图12可知，这是因为此时叶片的转速与来流风速方向一致，从而使得此时攻角α为0；当方位角θ=0°时，叶片的转速与来流风速方向相反由于安装角β=8°且叶片绝对速度最大，造成方位角θ=0°时叶片前缘产生的压差大于方位角θ=180°时叶片前缘产生的压差。此外值得注意的是，当尖速比λ=1.0且叶片旋转到方位角θ=90°时，叶片下翼面压差在前缘取得峰值之后演着弦线方向急速减少，在相对弦长x/c =0.35处压差趋近于0并且保持到尾缘处，这一现象意味着，气流在此处产生了分离现象，使得叶片进入了失速状态，这是由于低尖速比下，叶片转速较低，导致攻角α增大到失速攻角临界值；这一现象也出现在尖速比λ=1.8时，叶片下翼面在相对弦长x/c =0.7处出现了分离现象；此外随着尖速比的增加，压差值反而降低了，这是由于转速的增加导致攻角α变小，所以尖速比的增加也抑制了气流在叶片表面沿弦线方向上的分离。

4 结论

文章利用CFD数值模拟法对不同尖速比下三叶片Sb-VAWT的气动特性进行了研究，分析了转矩系数、功率系数和压力系数，可总结出以下结论：

1)叶片表面上下压差在叶片前缘处最大，并沿着弦线方向逐渐减小，在尾缘处趋于0。当叶片经过上流域的时候，叶片表面所受到的气动力达到最大值。随着尖速比的增加，压差逐渐减小。

2)在低尖速比λ=1.4和最佳尖速比λ=1.8时，叶片经过上流域发生了气流分离现象，增加尖速比能抑制气流分离。

3)随着尖速比的增加，转矩系数和功率系数不断增大到最大值；不同的是，单叶片在上流域的转矩系数峰值减少但功率系数峰值反而增大，最佳尖速比λ=1.8。