考虑前车动态扰动的改进车速在线预测方法

郭 兴，马 彬，2，3，姜文龙，陈 勇，2，3

(1. 北京信息科技大学机电学院，北京 100192；2. 新能源汽车北京实验室，北京 100192；3. 北京电动车辆协同创新中心，北京 100192；4. 中国人民公安大学交通管理学院，北京 100038)

1 引言

制定合理的预测能量管理策略对新能源汽车节能减排具有重要意义[1]。而高精度车速在线预测是制定高精度能量需求的关键，从而提高预测能量管理的效果，满足多工况能量管理的实时需求。然而，车辆行驶受周边车辆随机行为的影响，会发生一些加速、减速等行为，忽略前车动态行为的扰动的自车车速难以实现高精度预测。因此，进行自车车速高精度预测的同时，需要考虑前车动态行为的影响，提高非确定工况车速预测精度。

常用的车速预测方法主要是基于数据驱动预测算法[2]，结合车速历史数据或标准工况，利用相应估计和预测算法来对未来车速进行预测。冯安琪等[3]利用带遗忘因子自适应卡尔曼滤波实现了车速预测和调整；胡晓松等[4]采用自适应向量机、前馈神经网络和LSTM神经网络分别对行车速度进行预测，并对三种预测方法下方均根误差精度进行了对比；张金辉等[5]针对车辆跟车工况运动特性，使用贝叶斯网络方法对前车车速进行了预测；S Chao等[6]比较了指数、马尔科夫链和神经网络等车速预测精度，并将其结果作为MPC的参考信息构建预测能量管理策略，提高了车辆燃油经济性。

时间序列方法ARIMA具有自相关性和偏自相关性等特性，弥补了卡尔曼滤波、神经网络和马尔科夫链在非确定工况下预测精度不足的问题。张良力[7]等使用ARIMA模型进行道路交叉口的车速预测，并将此方法用于评估交叉路口车辆碰撞风险；Guo J等[8]开发了基于ARIMA模型的车速和坡度预测方法，并将其作为动态规划算法的参考轨迹用于开发车辆能量管理策略；冯安琪等[9]提出一种基于ARIMA模型的自适应卡尔曼滤波算法，利用预测加速度(ARIMA预测值)对车辆状态预测方程进行改进，进而通过带自适应遗忘因子的EKF循环迭代的方式实现车辆状态的预测，结果表明该算法预测精度获得显著提高。然而，上述研究忽略了前车动态行为对自车车速预测的影响，限制其预测精度的进一步提高。前车动态行为本质上是两车轨迹预测交互问题，通过驾驶员预判碰撞危险性对自车车速进行干预。当前，众多学者采用数据驱动的方法对车辆轨迹进行预测。季学武等[10]利用LSTM神经网络和MSD层，通过概率分布预测车辆位置；Deo等[11]通过卷积神经网络提取周围车辆特征信息，进而对车辆轨迹进行有效预测；李建平等[12]提出基于隐形马尔科夫链和高斯混合模型的车辆轨迹预测方法，预测精度得到有效提高。但是以上轨迹预测方法都是利用部分历史信息，限制了车辆轨迹预测效果。因此，考虑到极大似然估计法充分应用了每一个观测值所提供的信息，并具有估计一致性、渐进正态性和渐进有效性等许多优良的统计特性，将利用基于最大似然估计法的ARIMA模型实现轨迹预测。

综上所述，本文提出一种考虑前车动态扰动的改进车速在线预测方法，从而提高非确定工况车速预测精度。首先，在建立车辆运动学模型的基础上，基于EKF理论实现对自车和前车轨迹的构建；其次，以车车间纵向-横向安全距离为依据构建自车安全势场，基于历史轨迹数据利用ARIMA模型实现对自车和前车的轨迹预测和危险势场识别；然后，依据预测时域前车干扰危险势场，以交互点个数和安全势场边界间距为输入，建立基于模糊控制规则的自车车速预测调节器来修正车速ARIMA模型预测值；最后，结合自然驾驶实验数据，使用MARLAB软件仿真验证了所提出的改进车速在线预测方法的有效性。

2 基于EKF的车辆轨迹构建及验证

2.1 基于EKF的车辆轨迹建模

为准确描述车辆运动，将车辆运动简化为点的运动。并以自车为基准，通过自车和前车运动学关联特征构建自车和前车历史运动轨迹[13]，自车运动学模型为

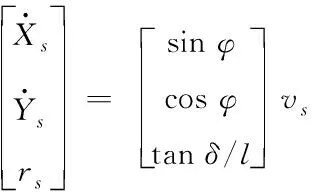
(1)

基于自车运动参数的前车运动学模型为

(2)

式中，Xo表示前车纵向位置；Yo表示前车横向位置；Δxs-o表示前车相对纵向距离；Δys-o表示前车相对横向距离。

由模型可知，构建车辆历史运动轨迹需要平稳、高精度的自车状态信息和前车相对位置信息，实验设备采集信息需要进行降噪处理。因此，采取EKF间接估计[14-15]的方法获取准确的车辆状态和位置信息，EKF最优估计过程如图1所示。

图1 EKF最优估计过程

2.2 轨迹构建数据采集和模型验证

搭建包含新能源电动车在内的数据采集系统，如图2所示。其中，姿态惯导和定位模块采集自车横、纵加速度和位置信息；拉线位移传感器采集方向盘转角信息；毫米波雷达采集前车相对位置信息。并使用EKF对采集数据进行预处理(如图3)。由结果可知，EKF降低了传感器噪声，实现了自车车速、横摆角、前车相对纵向距离和横向距离的最优估计。依据EKF估计信息构建的自车和前车历史运动轨迹结果如图4所示。由结果可知，基于运动学关联特征的自车和前车运动轨迹与真实结果吻合度较高，能够很好的反映车辆行驶时运动学特性，为后续车辆轨迹预测提供基础。

图2 实验设备

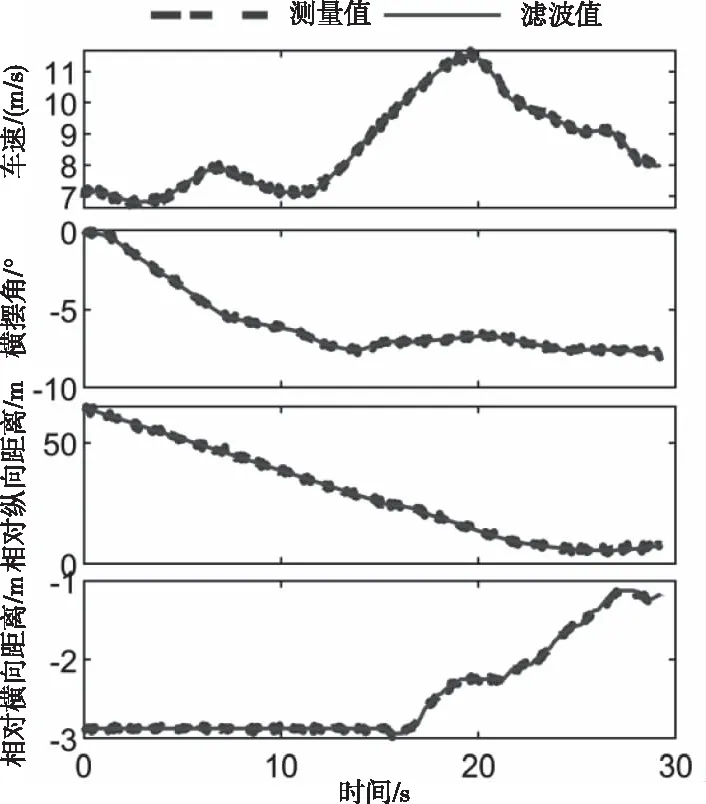
图3 EKF估计结果

图4 车辆轨迹构建结果

3 基于车辆轨迹预测的危险势场识别

3.1 基于ARIMA的车辆轨迹预测

ARIMA模型预测的本质是利用变量自身多期历史序列和预测误差实现自身预测。因此，本文以自车和前车历史轨迹序列为输入，通过构建轨迹ARIMA模型实现5s预测时域内自车和前车轨迹预测，ARIMA数学表达式[16]为

(3)

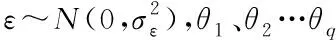
ARIMA建模及预测过程如下

Step1：利用ADF检验历史序列的平稳性，若非平稳，则采用差分法平稳化处理数据序列。

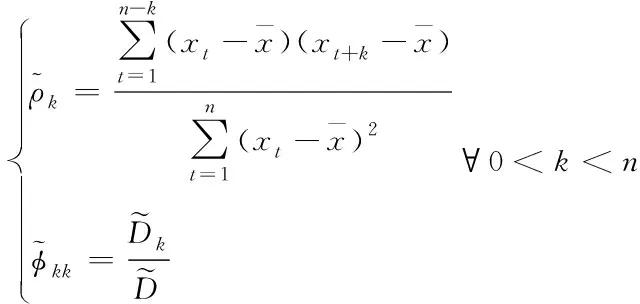
(4)

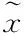
(5)

Step4：使用LB(Ljung-Box)检验模型残差序列的随机性，表达式为

(6)

Step5：利用最佳线性预测性质进行序列预测，其表达式为

(7)

通过上述建模、预测过程以及历史序列的滚动更新，即可实现轨迹ARIMA模型的轨迹在线预测。

3.2 自车安全势场建立及危险势场识别

车辆耦合运动特征下，前车动态干扰对自车轨迹和行车安全具有重要影响。基于自车和前车的预测轨迹，依据纵向和横向安全距离建立自车安全势场。纵向和横向安全距离表达式分别为[17]

(8)

(9)

式中，Xr表示纵向安全距离；Yr表示横向安全距离；X0表示最小纵向距离；Y0表示最小横向距离；T0表示总响应时间；vs表示自车纵向车速；vo＿xr表示前车相对纵向速度；vo＿yr表示前车相对横向速度；amax表示自车最大制动减速度。

采用交互点判断模型对预测时域内自车轨迹预测点的安全势场与对应前车轨迹预测点的交互关系进行判定，完成危险势场的识别，模型表达式为

in=inpolygon(Xo＿p(k)，Yo＿p(k)，Xr＿p(k)，Yr＿p(k))

(10)

式中，k表示预测步长；Xo＿p表示前车纵向预测位置；Yo＿p表示前车横向预测位置；Xr＿p表示自车预测位置纵向安全距离；Yr＿p表示自车预测位置横向安全距离；in=0 表示不存在交互点；in=1 表示存在交互点。

4 基于模糊调节的改进车速预测

ARIMA模型属于纯数据预测，因此同样使用ARIMA模型对车速进行预测。传统ARIMA预测模型具有对外部变量的独立性，忽略了外部信息对自身预测的指导作用。因此，本文利用模糊减速量对传统ARIMA模型预测步骤进行改进，构建改进车速ARIMA预测模型，将式(7)变为式(11)

(11)

式中，ΔVFuzzy表示模糊调节器输出的减速量。通过构建模糊调节器，实现减速量的实时调节。

研究表明[18]，前车切入和减速等动态干扰行为是影响自车车速变化的关键因素，但自车车速变化还受自车驾驶习惯等多种因素的影响，其相互关系呈现模糊特性[19]。因此，基于模糊控制策略建立考虑危险势场的车速调节器，从而实现自车车速预测值的模糊修正。选用预测时域内危险势场交互点数和交互点与危险势场边界平均间距为输入建立车速模糊调节器，通过识别自车危险程度输出相应减速量。模糊控制采用“Mamdani”方法；推理为“Max-Min”方法；解模糊化采用重心法；模糊语言采用“负大”(NB)，“负小”(NS)，“零”(ZO)，“正小”(PS)，“正大”(PB)；交互点数隶属度函数和模糊规则如图5和6所示。

图5 输入输出隶属度函数

图6 模糊规则

由图6可知，当自车安全势场内不存在交互点时，自车减速量ΔVFuzzy=0；当交互点存在且距自车距离越近时，自车减速量ΔVFuzzy>0，更加贴近车辆实际行驶工况。此外，车速ARIMA模型预测误差随预测步长增大而增大(表1)。可以看出，1s-3s预测误差较小，4s-5s预测误差较大。因此，车速模糊调节器只修正车速ARIMA模型的4s和5s车速预测值，以此方式提高车速预测精度。改进车速预测流程如图7所示。

表1 车速ARIMA模型预测误差

图7 改进车速预测流程

5 仿真分析

在自然驾驶数据中挑选前车切入和减速的行车工况，设置预测步长为5s，使用轨迹ARIMA(4，1)和车速ARIMA(3，1)模型分别实现车辆轨迹预测和速度预测。

5.1 车辆轨迹预测和危险势场识别结果及分析

1)前车切入工况

前车切入工况下的轨迹预测结果如图8所示。由图可知，自车在车道保持的情况下，起初ID12在自车道右前方的右侧车道行驶，车道保持行驶一段时间后切入自车道，自车开始跟随ID12平稳行驶；并且经轨迹ARIMA模型预测的自车和ID12轨迹与实际车车耦合运动轨迹相一致，为识别前车切入工况下危险势场提供条件。

图8 前车切入下的车辆轨迹预测

前车切入工况下车辆轨迹危险势场如图所9示。由图可知，结合自车安全势场，该算法在17s时预测到20s时刻自车与ID12首次出现交互点，而实际上自车在20s发生减速，与预测时间一致，并提前3s识别危险势场(红色实线框)。因此，前车切入工况下的自车安全势场可以有效预判自车危险势场。

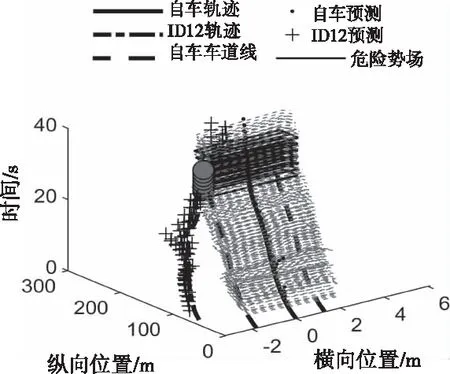
图9 前车切入下的车辆轨迹危险势场

2)前车减速工况

前车减速工况下的轨迹预测结果如图10所示。由图可知，起初自车道内自车跟随ID7正常行驶，随后ID7为避让自车道的障碍物，减速并靠右侧行驶以保证ID7自身安全；并且经轨迹ARIMA模型预测的自车和ID7轨迹正确反映了实际车车耦合运动状态，对识别前车减速工况下危险势场具有重要作用。

图10 前车减速下的车辆轨迹预测

前车减速工况下车辆危险势场如图11所示，由图可知，由于前车ID7的减速行驶，使得车间相对距离迅速减小，该算法在2s时预测到7s时刻ID7的轨迹预测点与自车安全势场首次出现交互点(黄色实心点)，而实际上自车在8s发生减速，与预测时间基本吻合，并且提前5s识别危险势场(红色实线框)。因此，前车减速工况下的危险势场可以起到有效的预警作用。

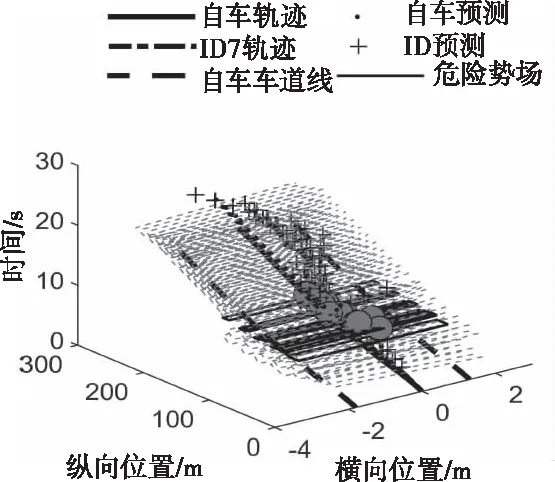
图11 前车减速下的车辆轨迹危险势场

5.2 改进车速预测结果及分析

1)前车切入工况

前车切入下的车速模糊调节结果如12图所示。由图可知，为应对ID12的切入行为，模糊调节器作用的时间段为17s-23s，对车速预测值进行修正，结果如图13所示。由图可知，传统ARIMA模型在自车平稳加速和减速工况下能够进行有效的车速预测，但其在前车切入的干扰工况下，未能预测到20s的自车减速的趋势，导致预测有较大偏差。而经过模糊调节器对自车车速预测值的修正，在前车切入期间，改进车速预测对自车车速变化趋势有良好的预判性。

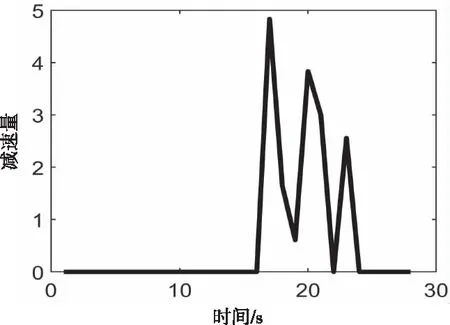
图12 前车切入下的预测减速量

图13 前车切入下的改进车速预测

2)前车减速工况

前车减速下的改进车速预测结果如图14所示。由图可知，由于ID7的减速行驶，模糊调节器在2s-6s时间段内工作，对车速预测值进行干预，结果如图15所示。由图可知，在前车平稳运行工况下，传统ARIAM模型可以对自车车速进行良好预测，但在8s时，由于其忽略了前车突然减速对自车车速的影。响，导致预测值有较大的偏差。而经过模糊调节器对自车车速预测值的修正，在前车减速期间，改进车速预测更加贴合实际车速。

图14 前车减速下的预测减速量

图15 前车减速下的改进车速预测

选取平均误差评价基于ARIMA的车辆轨迹预测和改进车速预测方法的有效性，前车切入和减速下轨迹和车速预测精度如表2所示。由表可知，在自车和前车耦合运动下，5s预测时域内自车和前车最大纵向预测误差为2.15m，最大横向预测误差为0.43m，满足轨迹预测要求；在两种前车动态扰动期间，改进车速预测误差分别为1.4m/s和3.77m/s，相比于传统ARIMA车速预测，分别提升了35.16%和56.62%，说明考虑前车动态扰动的改进车速在线预测方法能够有效预测自车减速行为，提高车速预测精度。

表2 前车切入和减速下轨迹和车速预测精度

6 结论

为提高前车动态扰动工况下自车速度预测精度，本文提出了考虑前车动态扰动的改进车速在线预测方法。首先，基于EKF和车辆运动学模型构建自车和前车轨迹；其次，结合自车安全势场和轨迹ARIMA模型实现自车和前车的轨迹预测以及危险势场的判别；最后，以危险势场内轨迹交互点参数为输入，自车预测减速量为输出，建立自车车速模糊调节器，实现对车速ARIMA模型的车速预测值的修正。结果表明： ①自车和前车轨迹预测纵向平均误差为1.9m，横向平均误差为0.29m； ②在前车切入和减速期间，相比于传统ARIMA预测，改进车速预测精度分别提高35.16%和56.62%。该方法为构建预测能量管理策略提供理论基础。