基于Spark的自适应蚁群算法对CVRP问题的求解

2022-02-09徐涛XUTao孙鉴SUNJian刘陈伟LIUChenwei

中兴通讯技术 2022年6期

徐涛/XU Tao，孙鉴/SUN Jian，2，刘陈伟/LIU Chenwei

（ 1.北方民族大学，中国银川 750021；2.图像图形智能处理国家民委重点实验室，中国银川 750021 ）

作为车辆路径问题（VRP）的一个分支，带有容量限制的车辆路径问题（CVRP）和旅行商问题（TSP）相比，约束条件复杂，问题规模大，求解难度高。VRP在物流配送中具有至关重要的作用，是运筹学和组合优化领域的研究热点，受到业界广泛关注。

VRP[1]是一种NP-hard问题，主要的解决方法有精确式算法、元启发式算法、机器学习算法等。分支限界法[2-3]及动态规划法[4-5]是精确式算法[6]的代表，可以有效求解小规模的CVRP问题。例如，对于数据集CVRPLIB①http://vrp.atd-lab.inf.puc-rio.br/index.php/en/中A类（set A）的27个实例，其节点规模在32～80之间[7]。但面对大规模问题，如数据集CVRPLIB中X类（Uchoa et al）的99个实例，节点规模在101～1 001之间[8]，计算复杂度较高，计算资源受限。强化学习[9-12]和深度学习[13-14]是机器学习算法的代表，但面对大规模CVRP的求解时间较长。蚁群算法[15]、模拟退火算法[16]、遗传算法[17]是元启发式算法的代表。此类算法更适用于大规模客户点的场景，能够在一个可接受的时间内得到一个相对可以接受的解。而蚁群算法由于具有蚂蚁搜索路径过程中并行的特点，结合分布式计算框架，可以有效提高解的效率。

蚁群算法本质上是一种并行算法，其中每只蚂蚁搜索路径的过程彼此独立。黄震华等[18]利用图形处理器（GPU）多线程并发的优势，提出中央处理器-图形处理器（CPUGPU）异构环境。该环境由CPU负责控制，同时由GPU完成大部分计算任务。每只蚂蚁被分配到统一计算设备架构（CUDA）的不同线程上。虽然能实现蚂蚁并行，但是这种异构环境依旧是单GPU多线程的单机环境。吴昊等[19]提出基于大数据环境MapReduce框架的蚁群算法。该算法用Map函数并行每只蚂蚁求解过程，用Reduce函数表达求得较优解和改变信息素过程，同时应用云计算的管道能力，把Re‐duce函数的输出信息作为下一代Map函数的输入，以进行下一代循环。这种蚁群算法在求解大规模的TSP问题上取得较好的结果。与MapReduce平台蚁群优化算法相比，王诏远等[20]提出的基于Spark平台的蚁群优化算法在解决TSP问题上的执行速度提升了10倍以上。

虽然上述并行算法能较好地解决CVRPLIB中A类及X类的VRP，但这些算法仍存在求解时间长、精度不高、平台架构限制大、扩展性差等缺陷。为此，本文中我们提出一种基于Spark平台的自适应蚁群算法（SPAMACO）。

本文中，我们首先针对蚁群算法信息素导向和启发信息权重进行自适应变化设计，摆脱固定参数的弊端；分段设计信息素强度变化，及时跳出局部最优解；针对求解精度差的问题，在产生局部解时利用2-opt算子增强算法局部搜索能力；针对大规模数据集执行时间过长问题，在Spark平台实现该并行算法，将蚁群封装成弹性分布式数据集（RDD），实现蚁群在分布式集群环境下的并行构造可行解，在减少算法执行时间的前提下保证了算法的求解精度。

1 技术介绍

1.1 CVRP问题描述

在图G= (V,E)中，顶点V={v0,v1,…,vn}，边E={(vi,vj),i≠j}。其中，v0表示仓库，vn为第n个客户点。每个客户的需求为ci，dij表示(vi,vj)的欧几里得距离，每辆车的最大载重为D。约束条件如下：

（1）每辆车都必须从仓库出发，并且返回仓库；

（2）每个客户点有且只有一辆车可以进行配送服务；

（3）一条线路上客户的总需求不能超过车辆的容量限制。

CVRP的目标是在这些节点当中确定一条最短的路径。集合K={1,2,3,…,k}表示运输车辆，车辆总数为k。集合P={pi={vi1,vi2,…,vir i}|r∈K}，使P中的k条路径距离和最小。其中，ri为由车辆i配送的客户节点数，vij为车辆i经过的第j+1个节点。建立模型的目标使车辆路径总长度最短。

1.2 蚁群算法

蚁群算法是M. DORIGO教授于1992年提出的。该算法源于蚂蚁觅食行为。蚂蚁在寻找食物时，会在经过的路径上释放一种信息素，并且能够感知其他蚂蚁释放的信息素。信息素浓度的大小表明路径的远近。信息素浓度越高，对应的路径距离越短。通常蚂蚁会以较大的概率优先选择信息素浓度高的路径，并且释放一定的信息素，使该条路径上的信息素浓度增高，进而使自己能够找到一条由巢穴到食物源最近的路径。但是路径上的信息素浓度会随着时间推移而逐渐衰减。

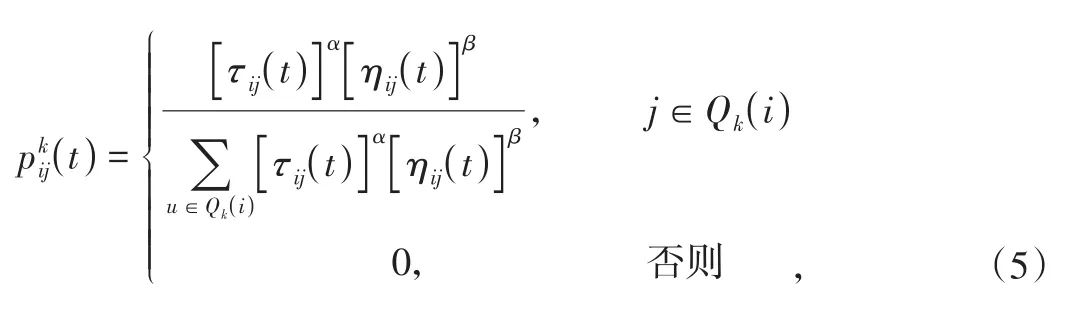
其中，Qk(i)={1,2,…,n}-τk表示蚂蚁k下一步允许选择的城市；列表τk记录这此次迭代中蚂蚁k的已访问城市，在接下来的遍历中不能再次访问列表τk中的城市；τij(t)表示t时刻路径(i,j)上信息素的数量；ηij表示启发因子，一般取路径(i,j)距离的倒数；α和β分别表示路径上的信息素累积量和启发信息的权重比例。

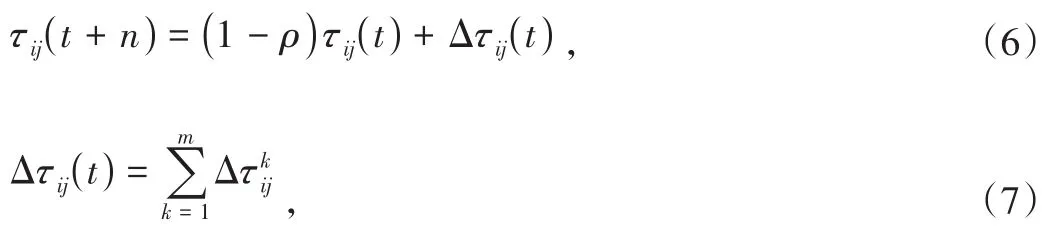
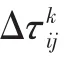
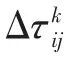
其中，Q为常数，Lk表示蚂蚁k在此次迭代中所走过的路径长度。

在蚁群算法求解CVRP方面，WANG X.[21]等提出一种新的ACO算法来求解CVRP。该算法允许蚂蚁多次进出仓库，直到它们访问所有客户。这简化了构建可行解的过程。LIN N.[22]等针对CVRP提出一种有效的顺序感知混合遗传算法。该算法的特征为改进的初始化策略和特定问题的交叉算子。前者结合了扫描算法，后者结合了邻域搜索启发式。S.AKPINAR[23]提出一种新的混合算法。该算法结合蚁群优化的解构造机制，执行大邻域搜索（移除和插入算子）方法来求解CVRP。R. GOEL[24]提出用蚁群和萤火虫算法（HAFA）的混合算法来求解CVRP，并在CVRP和带时间窗车辆路径问题（VRPTW）上做了验证。

1.3 局部搜索算子2-opt

2-opt算法是一种随机性算法，其基本思想是随机取两个元素进行优化，在路径问题求解上得到广泛应用。如图1所示，路径AD、BC。如果满足AD+BC＞AB+DC，则删除AD、AC并连接AB、DC，生成更短的路径。

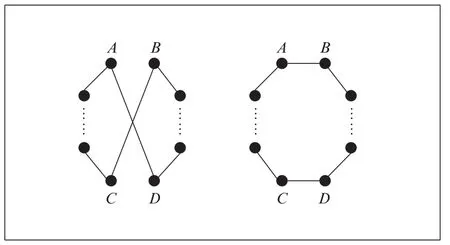
▲图1 2-opt算法优化过程

1.4 Spark计算框架

Spark是Apache软件基金会三大分布式计算系统开源项目，是基于内存的分布式计算平台。与MapReduce相比，Spark可以将计算中间结果存储在内存中，不需要反复读写分布式文件系统（HDFS），提高了计算速度，因此适合需要迭代处理的算法。Spark运行架构如图2所示。

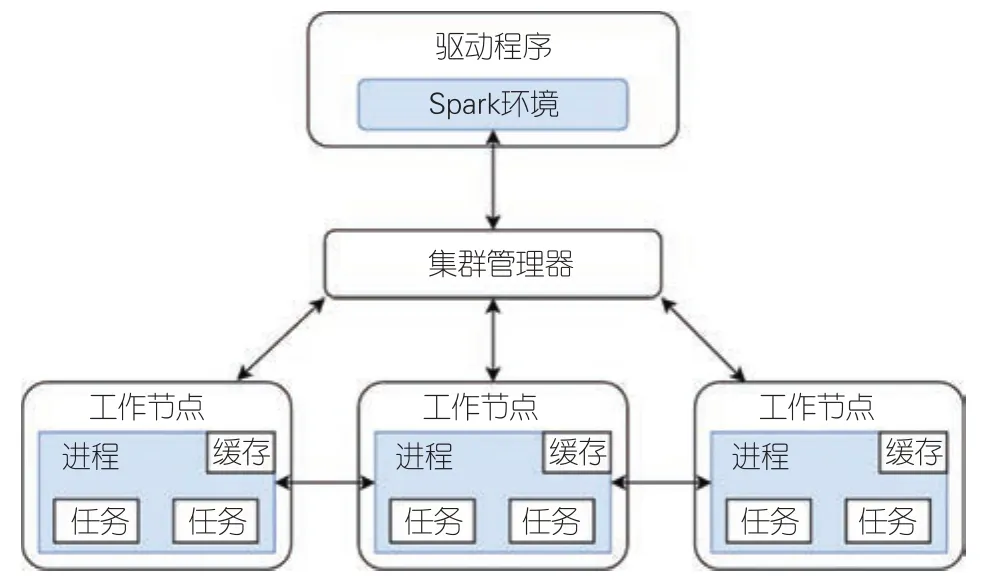
▲图2 Spark运行架构

Spark运行架构包括集群资源管理器、执行作业任务的工作节点、每个应用的任务控制节点和每个工作节点的执行进程。Spark所采用的进程有两个优点：一是用多线程执行具体任务，减少了启动开销；二是在执行进程中，会把内存和磁盘共同作为存储设备，有效减少了输入/输出（I/O）开销，提高了读写性能。

2 基于Spark框架的自适应蚁群算法设计

2.1 转移概率的改进

本文采用自适应调整选择概率来提高收敛性能。公式（9）中先进行的状态转换的选择操作，使得搜索个体倾向选择信息素浓度较高且路径长度较短的城市f。

其中，q是[0,1]区间的均匀分布的随机数；q0=2-arctan(ni+2)，(ni=1,2,…,iterations)，iterations为最大迭代次数。

2.2 信息素强度的动态调整

在前期，算法收敛比较慢；在后期，路径信息素浓度过大（容易造成局部最优）。对此，本文采用公式（11）中的分段函数代替常数Q。

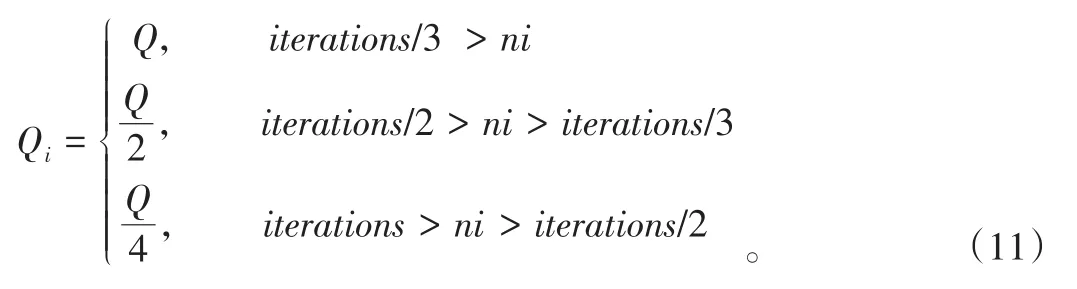
当最优解在一段时间内不变化时，搜索过程可能陷入局部最优困境。此时，分段的信息素设定可以增加或者减少信息素的数量影响。这使系统可以跳出局部最优困境。

2.3 自适应蚁群算法的并行化实现

用Spark平台可以完成自适应蚁群算法的并行实现。我们采用RDD进行操作，实现蚁群并行构建求解过程。

具体的SPAMACO步骤如下：

1）读取CVRPLIB数据文件，初始化车辆数量k、车辆容量D，构建坐标点（x,y）、客户点需求demand，计算各点距离，初始化信息素矩阵；

2）初始化参数；

3）封装蚂蚁为Ant类，利用Spark的.parallelize()操作将蚂蚁装换为分布式的RDD；

4）在每轮迭代中通过Spark的.map()方法实现并行求解过程；

5）每轮迭代结束后通过Spark的.collect()方法收集计算结果，对其进行2-opt局部优化；

6）更新信息素并广播；

7）判断迭代是否结束，结束输出全局最优解，否则返回步骤4继续并行计算求解。

综上所述，算法流程如图3所示。

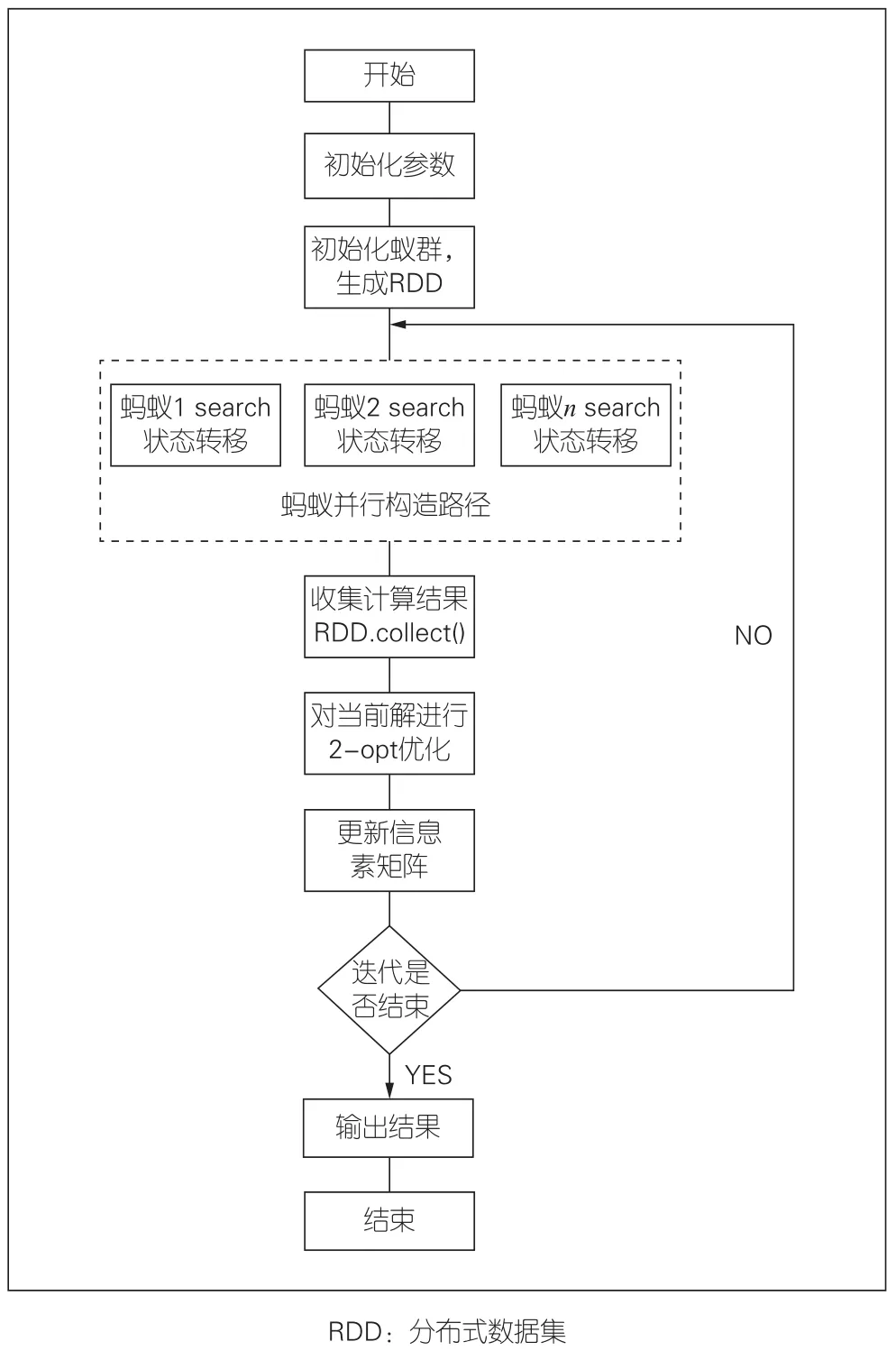
▲图3 基于Spark的自适应蚁群算法求解CVRP流程图

3 数值实验

3.1 实验设计

本文基于Spark分布式集群实现SPAMACO。实验环境由8台虚拟机组成，其中包括1台master主节点（负责任务控制节点的运行和管理），7台执行节点。

硬件配置：每台虚拟机CPU为四核四线程，内存为4 GB，磁盘容量为40 GB。操作系统是64位的Ubuntu18.04。

软件配置：Spark2.4.0、hadoop3.1.3、java1.8.0_162。实验中，我们采用具有函数式编程特性的python语言，同时为验证SPAMACO算法的有效性，采用自适应动态搜索蚁群算法（ADACO）[25]和自适应贪婪蚁群算法（GSACO）[26]作为对比实验。其中，为了保证公平性，GSACO和ADACO的参数选用原文中的参数设置。3个算法的迭代次数均为200次。

3.2 小规模算例实验结果

对于小规模算例，本文采用CVRPLIB中的A类数据集（SET A Benchmark），并选取 A-n60-k9、A-n61-k9、A-n62-k9、 A-n62-k10、 A-n63-K9、 A-n64-k9、 A-n65-k9、A-n69-k9、A-n80-k10进行求解。实验结果如表1所示，其中V表示当前算法最优解，T表示程序运行时间。

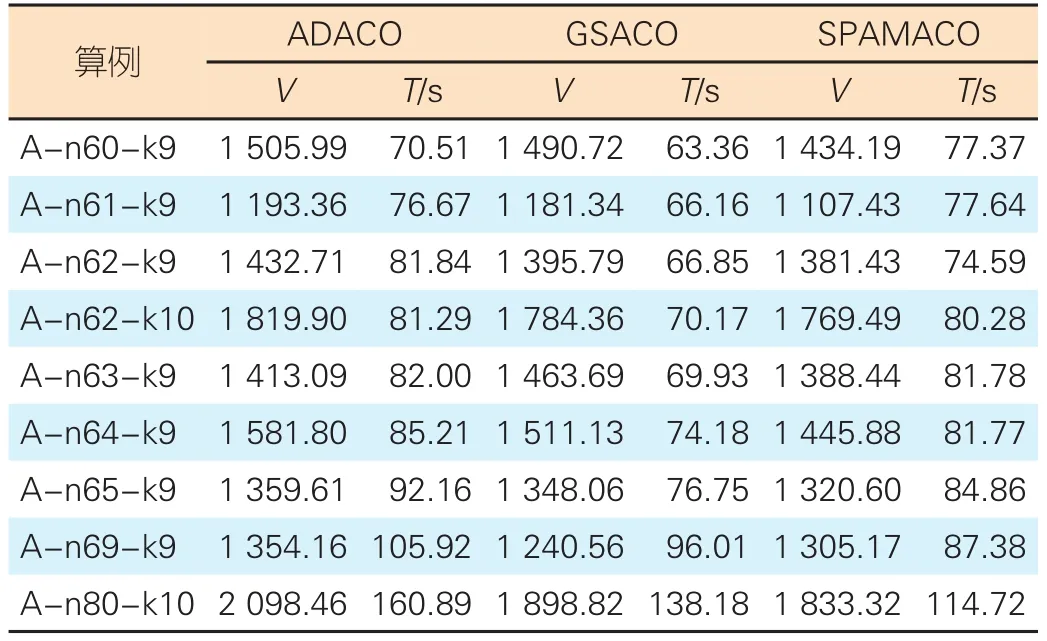
▼表1 小规模算例实验结果

从表1可以看出，和ADACO、GSACO相比，SPAMACO在求解精度上有所提升。但是由于受到Spark集群初始化时间、广播时间和组间通信等的影响，在小规模算例上，SPAMACO的运行时间优势并不明显。在客户点大于65后，并行的执行时间优势逐渐体现。在执行A-n80-k10算例时，本文算法执行时间比ADACO低28.8%，比GSACO低17%。

由图4可以看出，对于小规模算例，随着客户点数的增加，3个算法的执行时间会逐步增加。其中，除A-n80-k10以外，这种增加比例几乎相同。

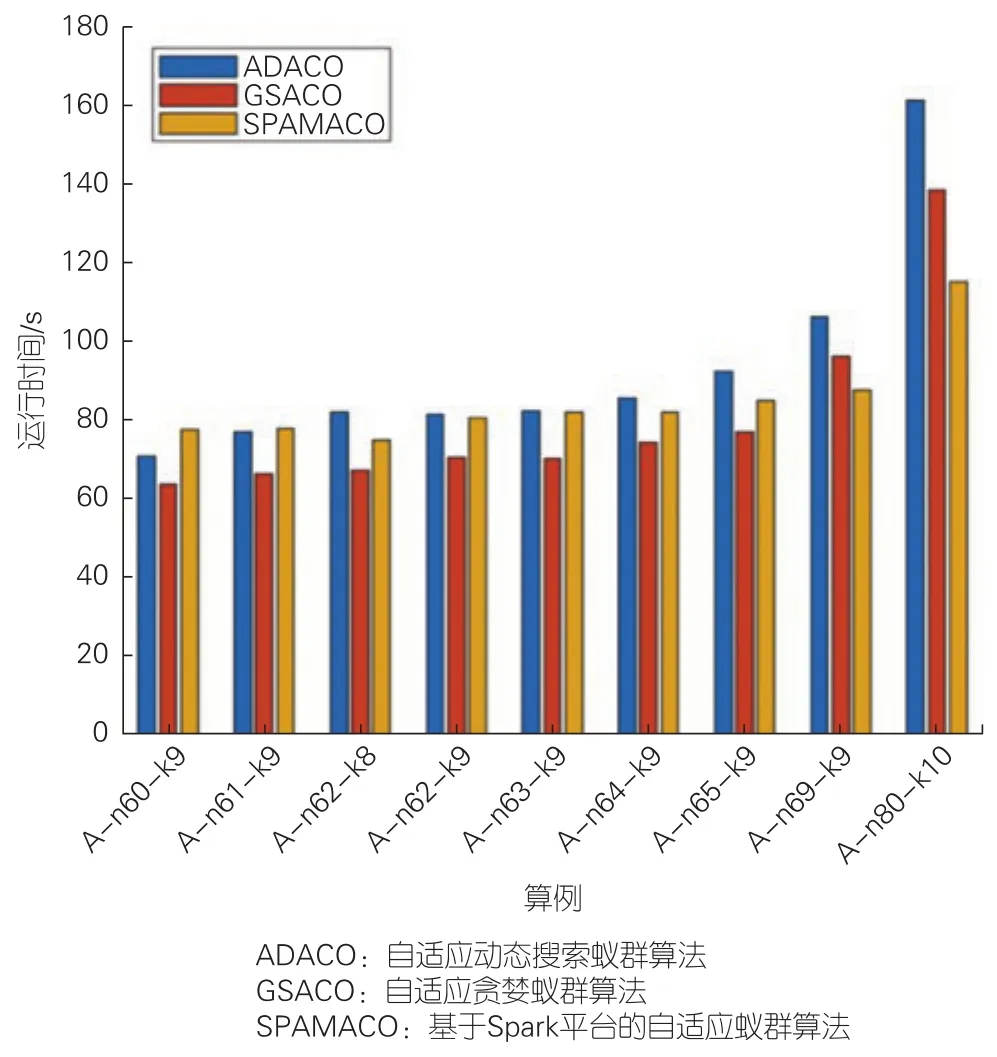
▲图4 小规模算例运行时间

3.3 大规模算例实验结果

对于大规模算例，本文采用CVRPLIB中的X类数据集（Uchoa et al. Benchmark），选取X-n101-k25、X-n106-k14、X-n148-k46、 X-n181-k23、 X-n200-k36、 X-n237-k14、X-n303-k21，并进行求解，结果如表2所示。

从图5可以看出，在大规模算例上（n＞100），随着客户点数的增加，ADACO和GSACO的执行时间呈指数增长，而本文所提算法的时间增加比率几乎不变。这是因为此时程序运行的大部分时间都是算法执行时间，同时Spark初始化、广播时间和组间通信所用时间占比也变小了。因此Spark基于内存的并行计算优势逐步体现出来。

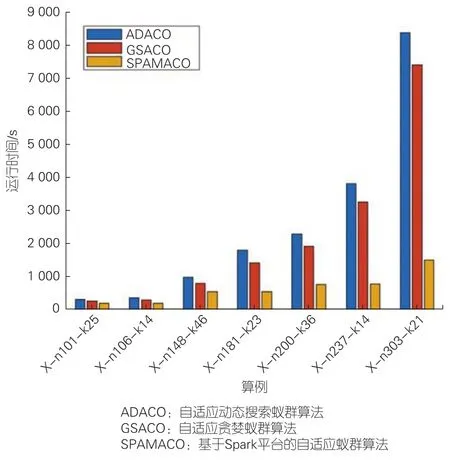
▲图5 大规模算例运行时间

在101个点时，本文所提算法的执行时间比ADACO快39.7%，比GSACO快29.0%。当客户点数增加时，如在200个点时，本文所提算法的执行时间比ADACO快66.6%，比GSACO快60.1%。在300个点时，本文所提算法的执行时间比ADACO快82.1%，比GSACO快79.7%。因此，SPAMACO更适合处理大规模算例，并且随着算例规模的增加，时间提升效果明显增加。